素土开挖边坡变形计算方法研究

魏焕卫，韩学民，王光金

(1.山东建筑大学 土木工程学院，山东 济南 250101;2.山东省城乡建设勘察院，山东 济南 250031;3.山东建筑大学管理工程学院，山东 济南 250101;4.山东省广播电影电视局，山东 济南 250001)

0 引言

素土开挖边坡在开挖前处于平衡状态，开挖后由于侧向卸荷引起应力的释放，首先表现坡体变形的增加，进而可能在坡顶地面出现裂缝，当坡顶裂缝继续发展时便可能出现边坡的整体或局部的坍塌破坏。传统大都通过边坡的整体稳定性安全系数来评价素土边坡的稳定性，先后提出了如圆弧滑动法、瑞典法、毕肖普法等多种研究稳定性的方法，而对于边坡变形的评价主要通过现场监测来实现。对于边坡安全性最直接的现场判断就是边坡变形的绝对值或其增速的大小，如GB50330－2002《建筑边坡工程技术规范》对于无支护边坡的变形控制条件给出了相应的标准[1]，但对于开挖素土边坡变形尚未有详细的计算方法，国内外已有的研究多集中在岩石边坡变形计算[2]、支护边坡变形计算[3－4]或数值计算[5－6]方面，除个别的模型试验[7－8]外，对于土体变形主要有虑变形的土压力计算理论的研究[9－10]，对于无支护素土边坡变形的理论方面研究的相对偏少。文章通过虚拟应力模拟素土边坡开挖工况，提出基于Mindlin解[11]的素土开挖边坡变形的计算方法，并通过计算对素土边坡的变形规律做了初步的探索。

1 素土边坡开挖的模拟和变形计算

1.1 边坡垂直开挖状态的模拟

基坑边坡未开挖前，在开挖面位置两侧存在一对大小相等方向相反的静止土压力，该静止土压力可以等效为预先施加大小等于静止土压力E0的弹簧(刚度系数为)(如图1a所示)。基坑边坡的开挖的过程就是原有静止土压力释放的过程，也等效为弹簧预加应力释放的过程，最终结果表现为开挖面位置应力释放至零，土体在开挖面位置产生一定的变形，如果按照等效弹簧分析，就相当于弹簧产生的回弹变形。通过在半无限土体中施加一个虚拟应力E(等于2E0，如图1 a所示)，就相当于在开挖面位置的由两个弹簧组成的平衡弹簧体系中是加了一个不平衡力，而新平衡产生的结果表现为一侧弹簧的预加力释放为零，另外一侧的弹簧预加力增加至2 E0，同时产生大小为的变形。由上述定性分析可以看出，采用在开挖面位置施加虚拟应力的方法模拟边坡土体的开挖从应力和变形方面都是可行的。

图1 边坡开挖前后应力－应变变化示意图

任意位置的虚拟应力底部应力大小为:

式中:k0为土的静止土压力系数;φ为土的内摩擦角，°;γ为土的重度，kN/m3;z为计算点深度，m。

1.2 直坡土体中释放应力和变形的计算

假定基坑开挖和影响范围内的土体是均质、各向同性的弹性体，在模拟状态下，引起土体变形的应力只有等于2倍静止土压力的虚拟应力，对用Mindlin解(图2)对应的应力和变形在开挖面数值积分就可以计算得到任意位置的应力和变形。

图2 作用在弹性半无限体中的水平向集中力

2 静止土压力系数计算

2.1 砂性土静止土压力系数的计算

雅基根据边坡角为φ的土坝中心线上的应力条件得出计算式:

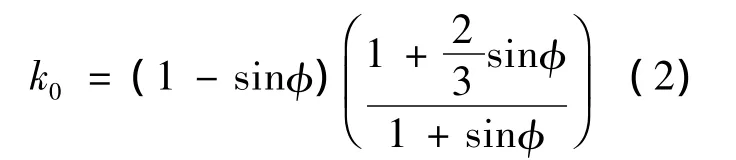
2.2 粘性土静止土压力系数的计算

波克罗夫斯基利用静力学的方法，考虑粘性土粘聚力而求得侧压力系数的关系式:

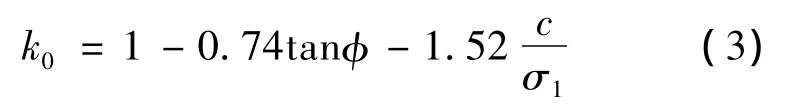
式中:σ1为垂直压力;c、φ为土的抗剪强度参数。

3 素土边坡开挖计算分析

3.1 计算参数

根据上述素土边坡变形的计算理论，以素土均质边坡开挖为例计算讨论不同因素对素土边坡土体变形的影响。边坡开挖深度和计算宽度均为6m，考虑分4步开挖，不考虑地面超载，直坡开挖。土体的各项计算参数取值(如表1所示)。

表1 边坡变形计算参数

按照上述计算理论和表1中的有关数据，通过计算讨论不同影响因素下边坡侧壁(开挖宽度中心线MN位置，如图3所示)侧向变形随深度的变化规律，以及坡顶(开挖宽度中心线MP位置，如图3所示)竖向变形随与开挖面距离的变化规律。

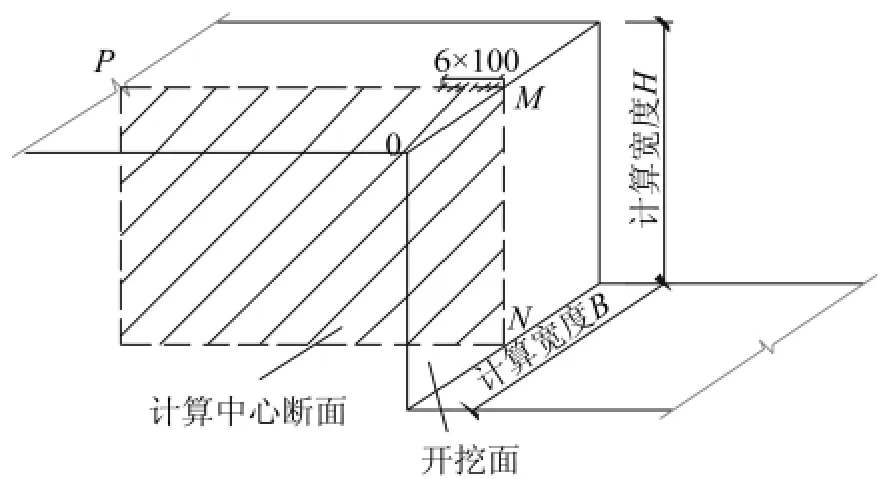
图3 边坡变形计算位置示意图

3.2 边坡坡壁侧向和竖向变形

由图4可以看出边坡壁侧向变形最大侧向变形点在边坡侧壁的中下部(约在边坡0.75倍开挖深度位置)，在采取措施控制边坡变形时，宜对该位置采取相对下部更强的加固措施。利用文章理论得到最大侧向变形位置与刘镇庭[6]通过离心模型试验得到的素土边坡最大侧向变形位置相近(如图5所示)，也与徐教宇[7]通过离心模型试验得到的素土边坡滑裂面和开挖面交点的位置相近(如图6所示)，同时也与工程现场素土边坡塌方滑坡体的位置相符(如图7所示)。同样边坡顶部的最大竖向变形点位于距离边坡开挖上边线约0.3H处，可以通过预托换或者跟踪注浆的方式对该范围内的坡顶建筑进行基础加固，避免因基坑开挖引起的建筑物倾斜或开裂等不良影响。

图4 边坡坡壁侧向和顶部竖向变形

图5 素土离心模型试验得到土质边坡水平位移曲线

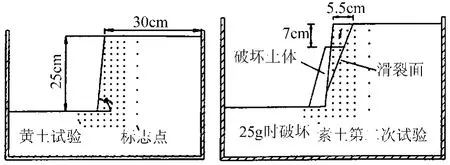
图6 素土离心模型试验结果示意图

图7 素土边坡塌方的现场照片

3.3 开挖深度对边坡坡壁变形的影响

图8为土体开挖深度H从2m到8m变化时边坡侧壁侧向变形和坡顶竖向变形随深度的变化规律，由图可以看出，随着H的增加，边坡的侧向变形和竖向变形都呈非线性增加，增加速率越来越大;其最大侧向变形的位置归于3/4H，其最大竖向变形的位置与开挖面的距离约为1/3H～1/2H;其最大侧向变形与HH的比值从0.55‰增加至1.94‰(如图8a所示)，这一点与刘镇庭[6]通过离心模型试验得到的素土边坡最大侧向变形与HH比值2.11‰相近(如图5所示)。

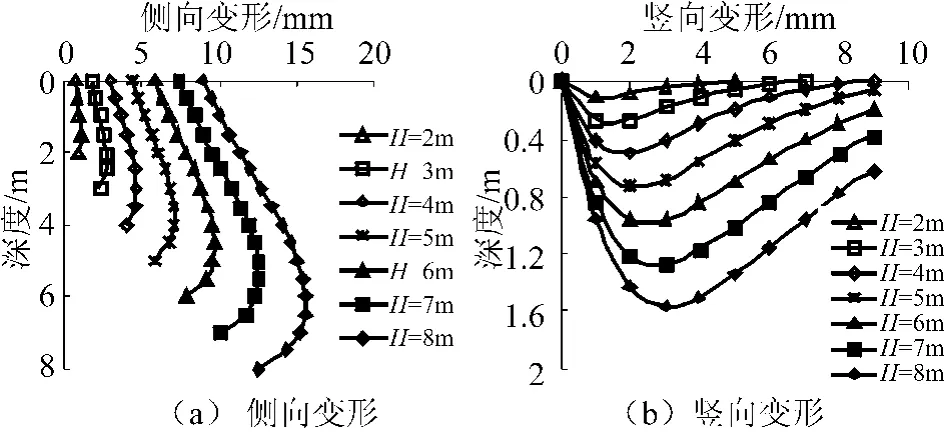
图8 不同土体开挖深度下边坡变形变化曲线

3.4 土体内摩擦角对坡壁变形的影响

图9为土体内摩擦角从15°到45°变化时边坡侧壁侧向变形和坡顶竖向变形随内摩擦角的变化规律，由图8中a、b可以看出，随着土体内摩擦角的增加，边坡的侧向变形和竖向变形都呈近似线性减小，其最大侧向变形的位置位于基坑开挖深度3/4H，其最大竖向变形的位置与开挖面的距离约为1/3H～1/2H(即开挖深度)。这是因为公式(2)计算粘性土的静止土压力随土体内摩擦角的增加而减小。

图9 不同内摩擦角下边坡变形变化曲线

3.5 土体内粘聚力对边坡坡壁变形的影响

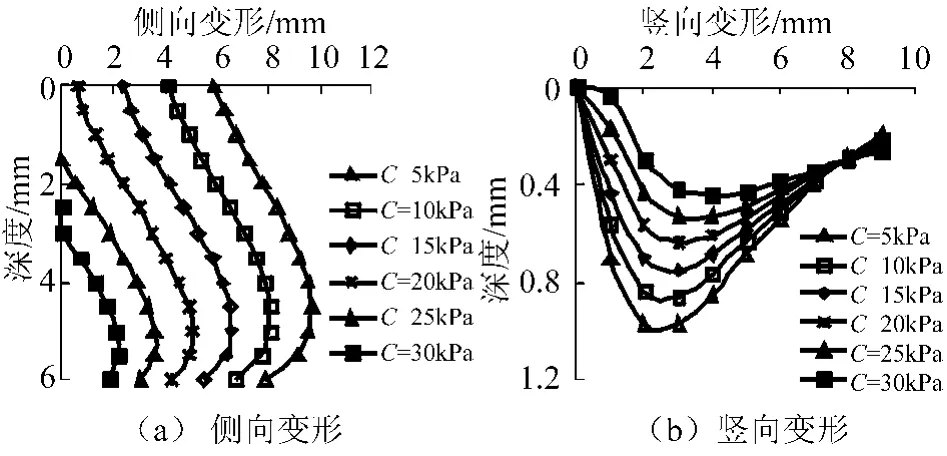
图10 不同内粘聚力下边坡变形变化曲线

图10为土体内粘聚力从5kPa到30kPa变化时边坡侧壁侧向变形和坡顶竖向变形随内粘聚力的变化规律的变化规律，由图9a、b可以看出，随着土体内粘聚力的增加，边坡的侧向变形和竖向变形都呈线性减小，其最大侧向变形和最大竖向变形的位置随土体内粘聚力变化规律与随土体内摩擦角变化规律类似。

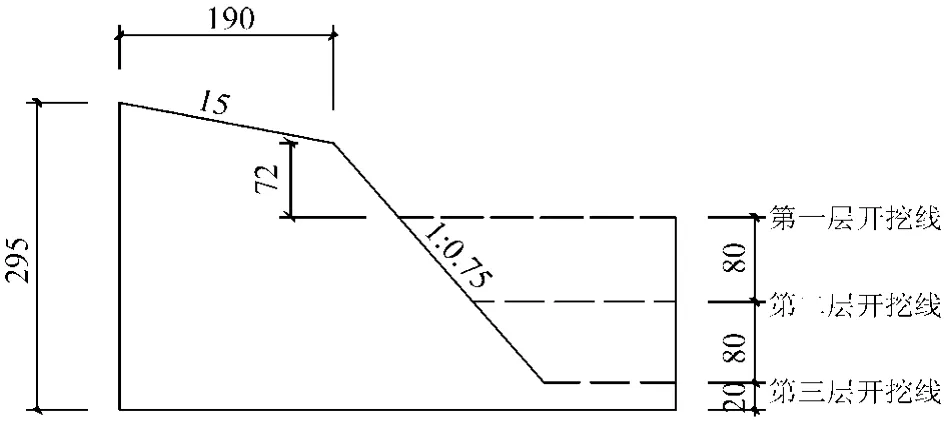
图11 土质边坡离心模型试验/mm

4 实测与计算对比分析

4.1 试验概况

文献[6]中土质边坡离心模型试验所用原材料参照重庆地区路边边坡常见土体类别取页岩风化土作试验材料，土的成型重度γ=20kN/m3，内粘聚力c=46.764kPa，内摩擦角 φ =20.54°，采用高度29.3cm、边坡坡度1:0.75来模拟高度29.5m的实际边坡，分三次开挖。根据离心模型试验的原理和等应力相似理论，当模型加速度放大n倍模型长度为原型的1/n时，模型采用原型材料，离心模型试验的相似比可以按照表2进行计算。

表2 等应力离心模型试验相似比(原型 /模型)

4.2 理论计算和实测对比分析

按照上述理论和计算参数，计算边坡开挖深度29.3m，边坡坡度1:0.75时的侧向变形曲线，由于离心模型试验中模型开挖高度为29.3cm，计算开挖深度与模型高度的比值为100，因此边坡侧向变形的理论计算结果应与离心模型试验中实测值的100倍进行对比分析。

由表2和图12可以看出，土体侧向变形的最大实测值出现在中部，而最大计算值出现在中下部，分析原因主要有两点:(1)实测土体下部变形受到模型箱底部阻力的影响较大;(2)理论计算中假定土体是均值的，而实际模型试验中土体可能是非均值的，由于重力作用表现为沿深度方向密实度逐渐增加的，因此下部土体的理论计算值要偏大。

图12 离心模型试验土体变形的实测值和计算值对比

5 结论

(1)文章提出虚拟释放应力的概念模拟土体开挖状态，通过等于2倍静止土压力的虚拟释放应力还原非弹性半无限体的开挖状态至弹性半无限体状态，假定土体为均质各向同性的弹性体，建立了基于Mindlin解的素土边坡位移计算方法。

(2)素土边坡土体的最大侧向变形点在边坡侧壁的中下部(约在边坡0.75倍开挖深度位置)，在采取措施控制边坡变形时，宜对该位置采取相对下部更强的加固措施;同样边坡顶部的最大竖向变形点位于距离边坡开挖上边线约0.3H处，可以通过预托换或者跟踪注浆的方式对该范围内的坡顶建筑进行基础加固，避免因基坑开挖引起的建筑物倾斜或开裂等不良影响。

(3)随着土体内摩擦角和内粘聚力的增加边坡的侧向变形和竖向变形都呈近似线性减小，其最大侧向变形的位置位于基坑开挖深度3/4H，其最大竖向变形的位置与开挖面的距离约为1/3H ～1/2H(即开挖深度)。

文章提出的素土边坡位移计算方法还需要通过与实测结果或经验值比较，后期将搜集更多的现场和室内实测资料对本方法的理论做进一步的验证和完善。

[1]JGJ120—99建筑基坑支护技术规程[S].北京:中国建筑工业出版社，1999.

[2]黄润秋，赵建军，巨能攀，等.汤屯高速公路顺层岩质边坡变形机制分析及治理对策研究[J].岩石力学与工程学报，2007，26(2):240－247.

[3]陈启辉，宋金平，江宗宝.微型桩与部分预应力复合土钉变形因素分析[J].山东建筑大学学报，2011，26(3):236 －239.

[4]魏焕卫，徐德亭，宋菲.侧向受荷桩基变形和受力规律的研究[J].山东建筑大学学报，2010，25(3):293 －296.

[5]张钦喜，孙家乐.插筋补强边坡变形与稳定性数值分析[J].岩土工程学报增刊，1992，14(S1):63 －91.

[6]吴顺川，张晓平，刘洋.基于颗粒元模拟的含软弱夹层类土质边坡变形破坏过程分析[J].岩土力学，2008，29(11):2899－2904.

[7]刘镇庭.边坡破坏机理的离心模型试验研究[J].公路交通技术，2002(6):67－80.

[8]徐教宇.土钉支护工作性状的研究[D].北京:中国建筑科学研究院，2003.

[9]卢坤林，杨扬.考虑位移影响的主动土压力近似计算方法[J].岩土力学，2009，30(2):553 －557.

[10]魏焕卫，杨敏，贾强，等.基于MINDLIN解土压力位移计算模型[J].岩土力学，2011，32(2):495 －502.

[11]Mindlin R.D..Force at a Point in the interior of a Semilinfinite Solid[J].Physics，1936(7):195 －204.