重心插值Galerkin 法求解梁弯曲变形问题

綦甲帅，王兆清

(山东建筑大学工程力学研究所，山东 济南 250101)

在处理梁弯曲问题时，经常遇到非连续载荷作用，解析方法需要在间断处分段，在每一段分别处理，然后在分段处通过施加连续性条件和边界条件来求解，导致积分常数很多，计算过程复杂。在这种情况下，常采用数值方法求解［1-3］。利用广义函数来表示非连续载荷的分布集度，不需要分段，可在全梁范围内建立统一的梁弯曲变形控制方程，使计算过程大为简化［4］。

最常用的广义函数是Delta 函数。这种函数最早出现于20 世纪30年代，是由著名物理学家Dirac［5］在量子力学研究中引入和定义的，后来被命名为Delta 函数。50年代Schwarz［6］在深入研究Delta 函数性质的基础上创立了分布论(亦称广义函数论)。2000年，Yavari 等［7-8］研究了广义函数在梁弯曲问题上的应用。Falsone［9］给出了利用广义函数Delta 函数分析不连续梁弯曲问题的解析方法。

有理函数插值有时比多项式插值具有更好的精度。在经典的有理插值中，对于给定的n +1 个节点，人们寻求如pM/qN的有理函数插值，其中pM、qN分别为次数不超过M、N 的多项式，且M+N=n。这种有理函数的主要缺点是，在插值区间内无法控制极点的产生。Berrut 等［10］提出利用高次多项式来构造有理函数插值，这样可以避免插值区间内极点的产生。2005年，Berrut 等［11］对重心型有理函数插值作了总结，利用n 次多项式构造的有理函数插值，可以写成重心形式。2006年Floater 等［12］提出一类重心型有理函数插值，该插值在整个数轴上都不存在极点，插值函数具有无穷次光滑性。基于微分方程弱形式的Galerkin 法［13］，可以降低近似函数的连续性要求，并且利用Delta 函数关于积分的筛选性，Galerkin 法可以消除求解问题中的奇异项［14］。

本文利用重心有理插值函数作为试函数，运用广义函数建立梁弯曲变形的控制方程，利用Delta 函数的积分筛选性，提出求解梁弯曲变形问题的重心插值Galerkin 法。

1 广义函数定义

(1)Heaviside 函数定义为:

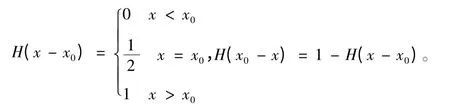
(2)Delta 函数也称为脉冲函数，其一般定义为:

2 重心有理插值Galerkin 法

以重心有理插值作为试函数，采用Galerkin 法建立数值求解梁弯曲变形控制方程的公式。对于在集度为q(x)的荷载作用下的细长梁，在弹性范围内发生线性弯曲，其控制方程为:

采用加权残数法建立方程(1)的积分弱形式，取加权函数W，有

对方程左边分部积分二次，可得

式中，W 为加权函数。在Galerkin 法中，权函数取为插值的基函数。

对于求解区间的一组节点0=x1＜x2＜… ＜xn=l，通过重心有理插值，梁的挠度可写成

式中，φk(x)为重心有理插值基函数。

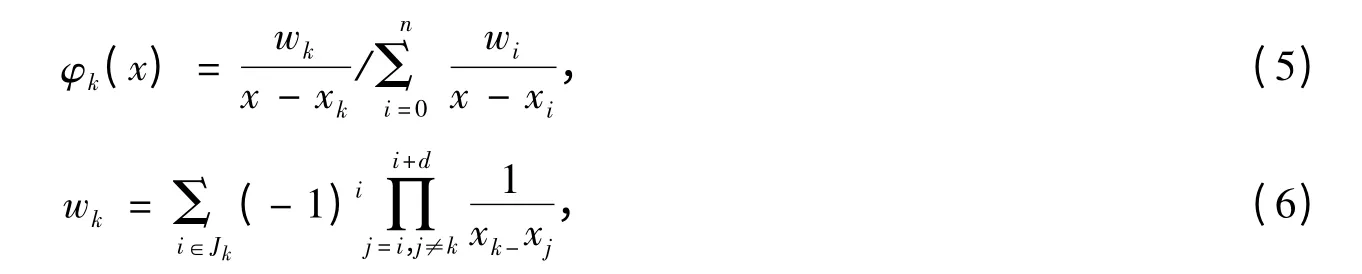
Jk={i ∈I:k－ d ≤i ≤k}，I={0，1，2，…，n}，d 为重心有理插值参数，满足0 ≤d ≤n。

在Galerkin 过程中，令Wk=φk，将φk(x)代入(3)式得到

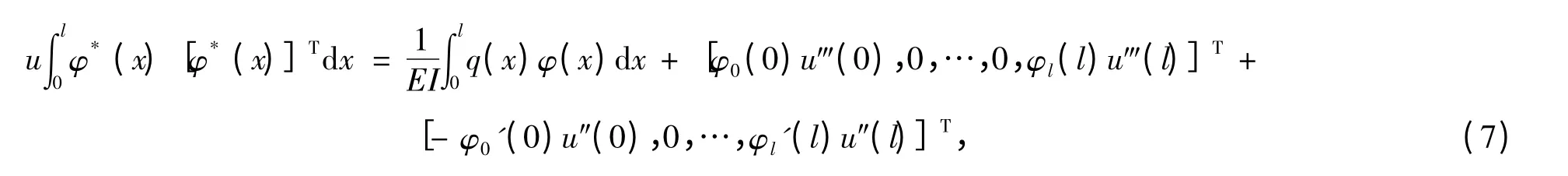
其中φ(x)=［φ0(x)，φ1(x)，…，φn(x)］T，u=(u0，u1，…，un)T。方程(7)写成矩阵的形式为

通过施加边界条件，可以消除向量b 的未知导数。由于插值基函数为有理函数形式，采用数值积分计算矩阵A 和向量b。

3 数值算例

本文算例的计算程序采用MATLAB 编写，除了主程序外，还有计算基函数及其一阶导数、二阶导数的子函数和施加边界条件的子函数。

图1 梁受集中力载荷Fig.1 An beam with concentrated load

算例1 两端简支梁，长L=50 cm，高2 cm，宽1 cm，弹性模量为10 GPa，受如图1 所示集中力F=50 N，集中力作用于梁跨中，运用广义函数表示的载荷集度q(x)=Fδ(x-x0)，x0为集中力作用点。计算节点采用等距节点，Galerkin 法中的积分采用小区间［xi，xi+1］上的3 点Gauss数值积分计算，插值参数d=4。梁各点的相对误差和绝对误差分别定义为Er=|uc-ue|/|ue|，Ea=|uc-ue|。不同数量节点计算的相对误差和绝对误差分别定义为Er=‖uc-ue‖2/‖ue‖2，Ea=‖uc-ue‖2，其中uc，ue分别为函数的数值计算值和解析解值列向量，‖·‖2为向量的2 范数。数值计算得到梁轴线的各节点挠度、转角、弯矩与解析解比较如表1 所示(选取30 个节点计算，表中只列举了有代表性的11 个节点)，不同数量节点计算误差如表2 所示，解析解见文献［15］。

表1 算例1 梁各点挠度、转角和弯矩解析解与本文解比较Table 1 The comparion of analytical solution and the presented solution of beam deflection，angle and moment of each point for instance 1

算例2 受如图2 所示荷载，q=200 N/m，其他参数同算例1，运用广义函数表示的载荷集度q(x)=qH(x-xi)，得到梁轴线的各节点挠度、转角、弯矩与解析解比较如表3 所示(选取30 个节点计算，表中只列举了有代表性的11 个节点)，不同数量节点计算误差如表4 所示。

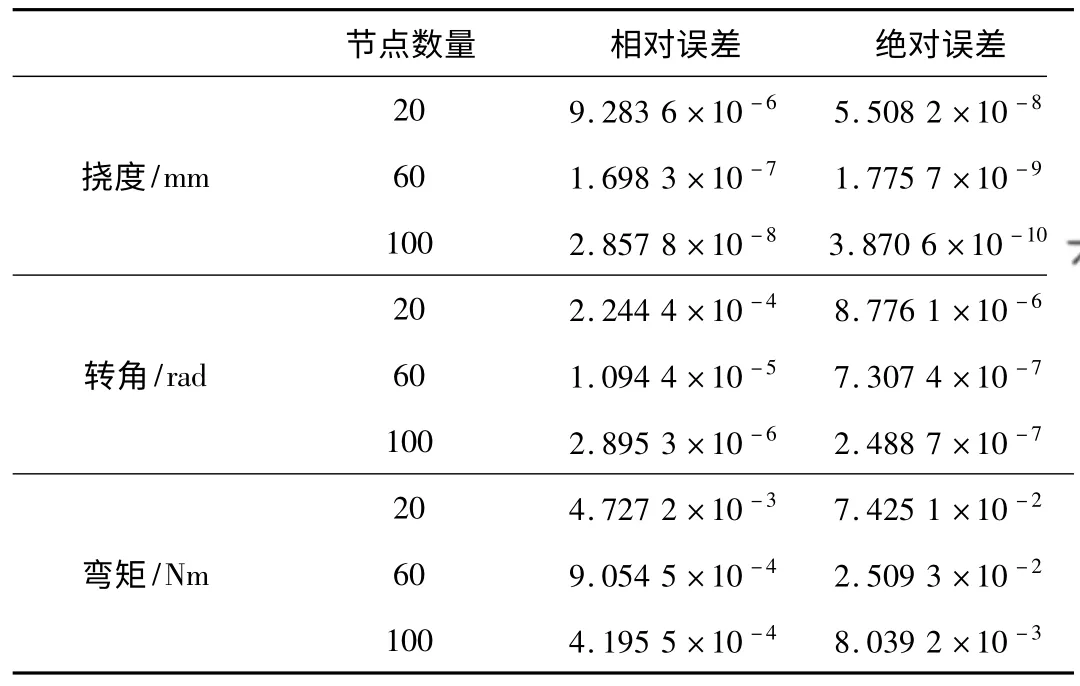
表2 算例1 不同数量节点的相对误差和绝对误差Table 2 Relative and absdute errors of different number of nodes for instance 1

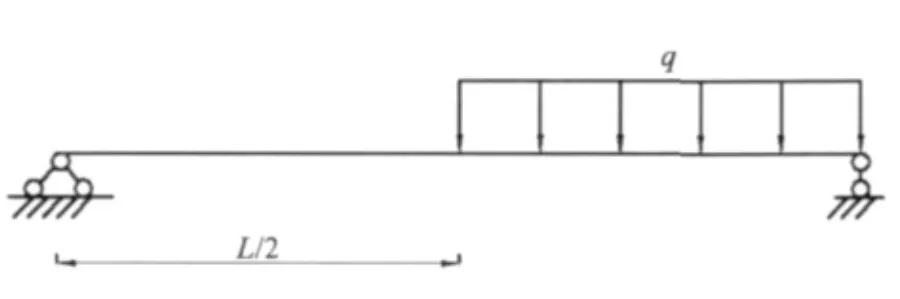
图2 梁受部分均布载荷Fig.2 An beam with partial uniform load

表3 算例2 梁各点挠度、转角和弯矩解析解与本文解比较Table 3 The comparion of analytical solution and the presented solution of beam deflection，angle and moment of each point for instance 2

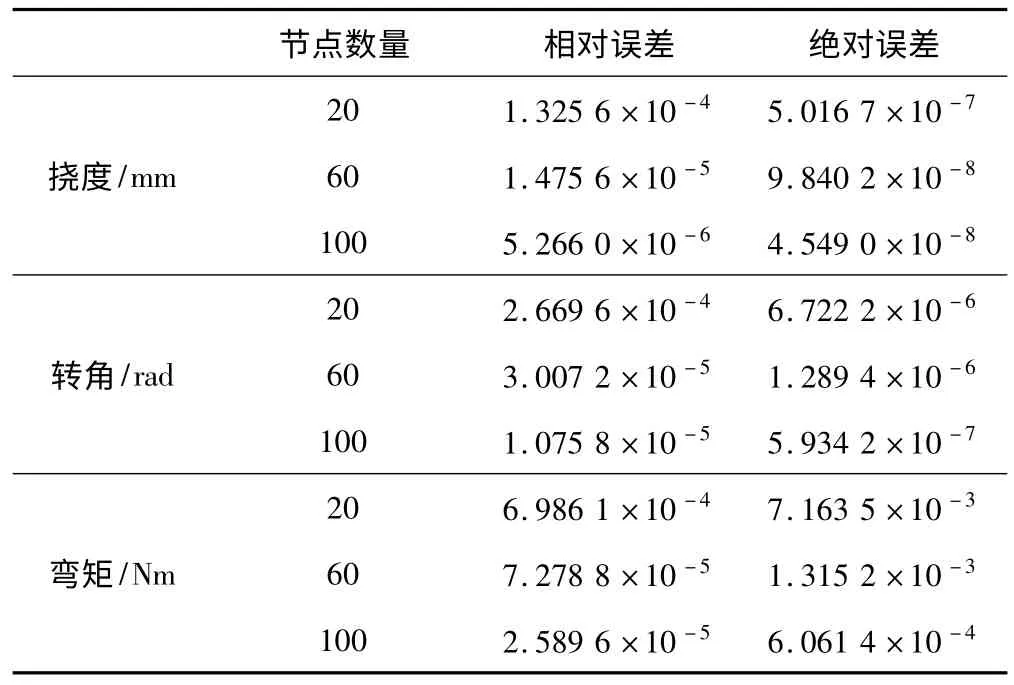
表4 算例2 不同数量节点的计算相对误差和绝对误差Table 4 Relative and absolate errors of different number of nodes for instance 2

算例3 受如图3 所示部分三角形荷载，q=200 N/m，其他参数同算例1，运用广义函数表示的载荷集度q(x)=qxH(x -xi)/L，得到梁轴线的各节点挠度、转角、弯矩与解析解比较如表5 所示(选取30 个节点计算，表中只列举了有代表性的11 个节点)，不同数量节点计算误差如表6 所示。

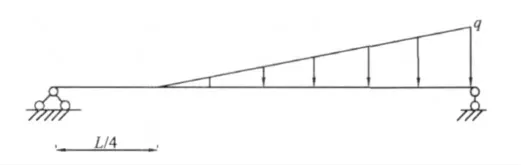
图3 梁受部分三角形载荷Fig.3 An beam with partial triangular load

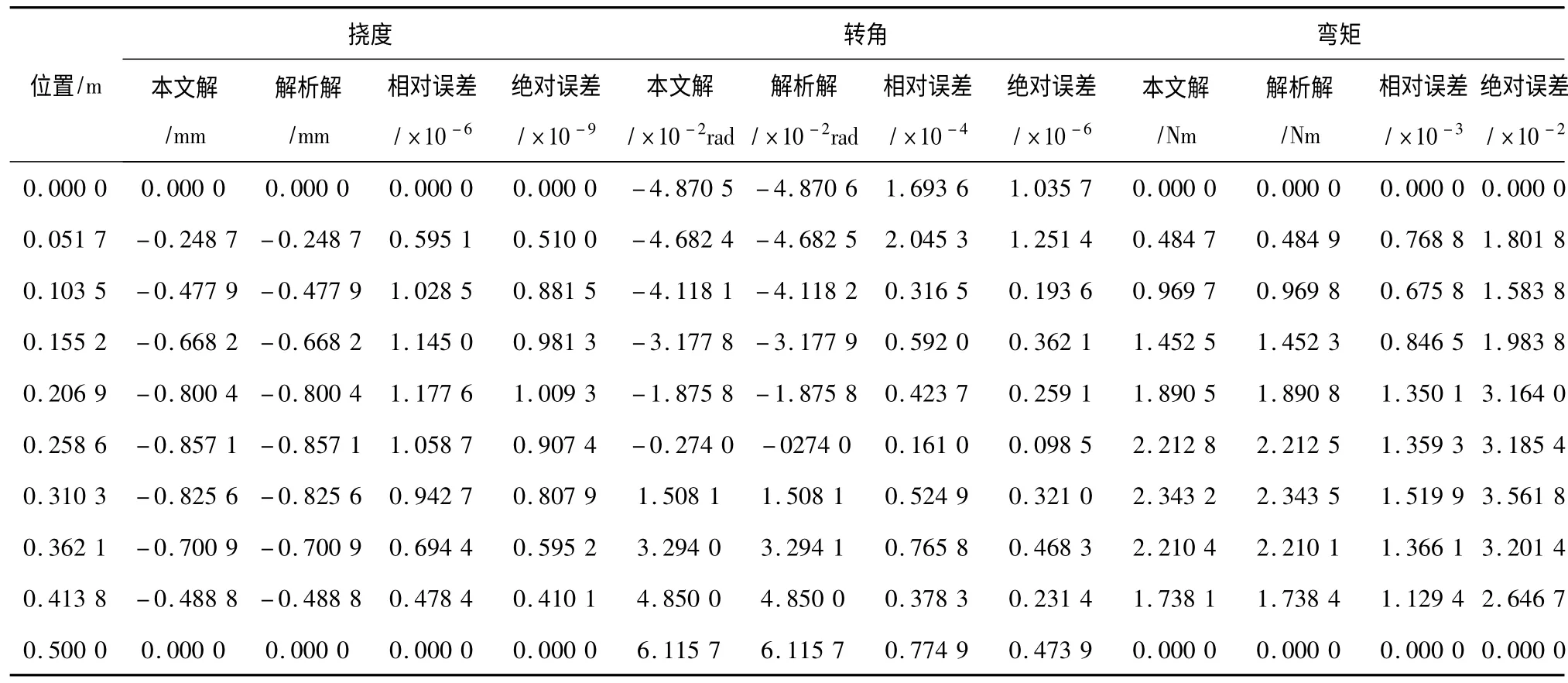
表5 算例3 梁各点挠度、转角和弯矩解析解与本文解比较Table 5 The comparion of analytical solution and the presented solution of beam deflection，angle and moment of each point for instance 3

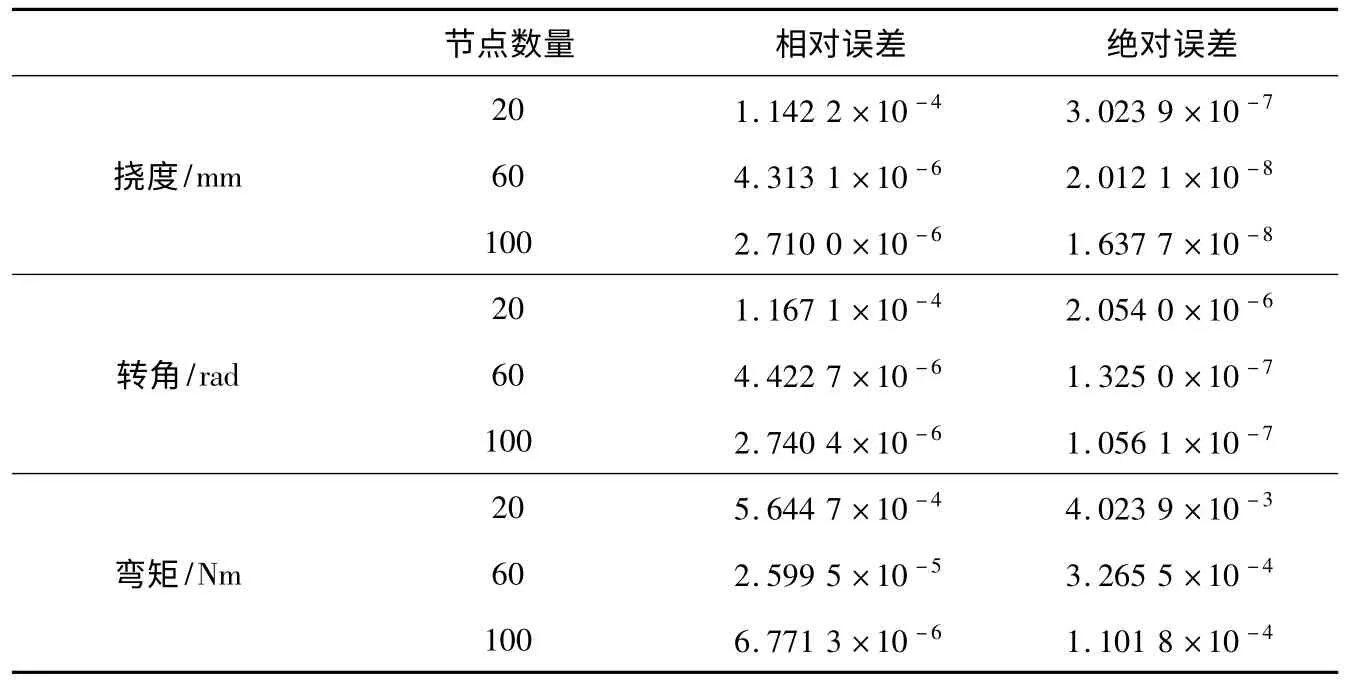
表6 算例3 不同数量节点计算相对误差Table 6 Relative and absolate errors of different number of nodes for instance 3

分析上述3 个数值算例的结果，可以得出以下结论:(1)重心有理插值Galerkin 法有很好的精度，并且计算精度随计算节点数量的增加而提高;(2)由于求导过程中丧失精度，因此转角和弯矩的精度比挠度的精度差一些;(3)算例1 中的计算精度高于算例2、3，是因为算例1 中的未知函数比算例2、3 中的光滑性好。

4 结论

重心有理插值Galerkin 法可以快速的求解梁弯曲变形问题，并得到具有无穷次光滑性质的数值解。对于非连续载荷等复杂载荷的计算，利用广义函数以及Delta 函数的积分筛选性建立梁弯曲变形的控制方程，不需要分段，大大简化了求解过程，并且少量的节点即可得到较高的精度，为这类问题提供了新的方法和思路。该方法原理简单，易于程序实现，在力学和结构分析中有良好的应用前景。

［1］VIRDI K S.Finite difference method for nonliear analysis of structures［J］.Journal of Constructional Steel Research，2006，62(11):1210 -1218.

［2］RAJU I S，PHILLIPS D R，KRISHNAMURTHY T.A Meshless Method Using Radial Basis Functions for Beam Bending Problems［EB/OL］.［2012 -09 -11］http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20040191554_2004198262.pdf.

［3］袁玉全，彭建设.复杂载荷下梁弯曲问题的微分求积法应用研究［J］.四川理工学院学报:自然科学版，2006，19(5):81 -84.

［4］曾纪鹏.用奇异函数建立变参数连续梁挠度统一方程的新方法［J］.四川建筑，2011，1(1):128 -130.

［5］DIRAC P A M.The principles of quantum mechanics［M］.Oxford:Oxford University Press，1930.

［6］SCHWARZ L.Theory of distributions［M］.Paris:Hermann，1966.

［7］YAVARI A，SARKANI S，MOYER E T.On applications of generalized functions to beam bending problems［J］.International Journal of Solids and Structures，2000，37(40):5675 -5705.

［8］YAVARI A，SARKANI S.On applications of generalized functions to the analysis of Euler-Bernoulli beam-columns with jump discontinuities［J］.International Journal of Mechanical Sciences，2001，43(6):1543 -1562.

［9］FALSONE G.The use of generalised functions in the discontinuous beam bending differential equations［J］.International Journal of Engineering Education，2002，18(3):337 -343.

［10］BERRUT J P，MITTELMANN H D.Lebesgue constant minimizing linear rational interpolation of continuous functions over the interval［J］.Computational Mathematics and Applications，1997，33(6):77 -86.

［11］BERRUT J P，BALTENSPERGER R，MITTELMANN H D.Recent developments in barycentric rational interpolation［J］.International Series of Numerical Mathematics，2005，151:27 -51.

［12］FLOATER M S，HORMANN K.Barycentric Rational Interpolation with no poles and high rates of approximation［J］.Numerische Mathematik，2007，107(2):315 -331.

［13］王兆清，李树忱，唐炳涛，等.求解两点边值问题的有理插值Galerkin 法［J］.山东建筑大学学报，2008，23(4):283 -286.

［14］王兆清，綦甲帅，唐炳涛.奇异源项问题的重心插值数值解［J］.计算物理，2011，28(6):883 -888.

［15］刘鸿文.材料力学［M］.4 版.北京:高等教育出版社，2004.