基于负二项回归模型的高速公路交通事故影响因素分析

夏萍萍 ，魏丽英，马壮林

(1.北京交通大学交通运输学院，北京 100044;2.长安大学汽车学院，陕西 西安 710064)

截至2011年底，我国高速公路里程已达8.5 万km。高速公路里程的逐年增加，方便了人们的出行，促进了社会的发展，但也突显了我国重特大交通事故频发的高速公路安全性问题。据统计，2010年我国高速公路里程占公路通车总里程的1.85%，而其事故起数和死亡人数分别占公路交通事故总数的7.76%和13.54%;高速公路百公里事故率和死亡率分别约为普通公路的4.47 和8.31 倍［1］。由此可见，我国亟需提高对高速公路交通安全的重视程度，加强对高速公路交通事故影响因素的专题研究，从而改善我国高速公路的安全现状。

国内外学者先后在事故致因机理方面开展了较为丰富的研究。Poch 等［2］搜集了63 个十字交叉口7年的事故数据，运用负二项回归拟合了入口水平的追尾事故起数模型。Yan 等［3］运用双重逻辑回归模型对事故点车道数、限速值等因素进行了信号交叉口事故特征的研究。Wang 等［4］采用带有不同关联函数的广义估计方程对信号交叉口追尾事故起数建模，结果表明追尾事故间有很高的相关性。Chang［5］分别采用负二项回归和人工神经网络算法，构建了高速公路交通事故的起数模型。张生瑞等［6］结合高速公路隧道交通事故的特点及隧道出入口的道路特征，进行了事故多发段的成因分析，提出了隧道群交通事故的预防对策。马明等［7］利用基于3 种作业相关结构的广义估计方程负二项模型拟合了87 个信号交叉口的事故数据，结果表明基于自回归型相关结构的广义估计方程回归模型拟合效果最优。但是，现有成果大多以针对信号交叉口和高速公路隧道群等特殊事故点的追尾事故的研究为主，而面向高速公路全路段各种形态交通事故的系统性研究还不多见。

本文较为深入地剖析了高速公路交通事故的主要影响因素，构建了基于负二项回归的高速公路交通事故时空分析模型，量化分析了各种时空因素对交通事故的影响程度，最后以某高速公路典型危险路段为例，验证了模型的可用性。

1 致因分析与变量遴选

以系统观点来看，交通事故是由人、车、路、环境间的不协调所致。单从时间角度分析，事故率与交通量大致呈“U”形关系，与交通组成和不良天气存在某些联系［8-9］;单从空间角度分析，道路平纵线形及线形组合影响着交通事故的发生。本文采用定长法将研究对象划分为若干路段，每段长度为1 km，从时间和空间角度选取9 个候选自变量，以每一路段的年交通事故起数为因变量，构建高速公路交通事故时空分析模型。各候选自变量概念如下，部分自变量公式见表1。

(1)交通量。表示在指定时段内，通过道路某一断面或某一车道的交通实体数。本文以研究对象的年平均日交通量对数作为模型的自变量。

(2)大车比例。本文以载重超过5 t 的货车和座位超过19 座的客车之和来计算大车比例。

(3)弯曲比。表示在指定路段内，曲线长度之和占路段总长的比例，记作Ri。

(4)平均曲率。表示在指定路段内，各线形要素曲率的平均值，记作Ci。

(5)曲率变化率。表示在指定路段内，单位长度平曲线的角度变化之和，记作Ki。

(6)曲线频率。表示在指定路段内，含有不同类型、不同半径的曲线的条数，记作Fi。本文以1 km 定长路段为单位，清算每一路段内包含的曲线数量。

(7)平均坡度。表示在指定路段内，纵坡坡度的加权平均值，记作Gi。

表1 自变量计算公式Table 1 Formula of independent variables

(8)连续下坡累积效应。高速公路连续下坡对车辆制动性能的影响有明显的“后效性”，即从坡顶出发，行驶距离越长，制动器性能下降幅度越大，直至制动器“热衰退”而失效，引发交通事故。为描述连续下坡路段对行车安全的这种影响，受土壤学中“地形因子”［10］的启发，本文提出长大下坡路段“连续下坡累积效应”的概念，将其定义如下:

首先，计算第l 个路段的坡度因子Sl和坡长因子Ll，进而计算改善的LS 因子El。其次，假设当累积下坡长度超过5 km 时，相邻坡段之间存在指数影响关系［11］，计算第l -1 个坡段对第l 个坡段的影响系数Fl。最后，计算第i 个路段的连续下坡累积效应Di。

整个计算过程如下:

其中θl，λl分别为第l 个纵坡的坡度和坡长(转换为角度)，Gl为第l 个坡段的纵坡坡度(%)，Lil为位于第i 个路段内的第l 个坡段的长度。

(9)连续转弯。为衡量高速公路平面线形的连续性，本文提出“连续转弯”的概念，将其定义为在某一研究路段内，是否存在相邻的两个或两个以上转向相反的弯道的情况。由此可见，连续转弯是一个二元变量，如果第i 个路段内存在两条或两条以上转向相反的平曲线，那么该路段的连续转弯值就取为1;反之，连续转弯值取为0。

2 交通事故分析模型

2.1 事故分析模型构建

高速公路交通事故起数属于离散型计数数据，通常可以采用泊松回归模型来进行离散型计数数据的处理。泊松回归以事件起数Y 为研究对象，以y 表示事件起数的观测值，假设事件的发生遵循泊松分布，随机变量Y 等于y 的概率，则其分布密度函数为

然而，泊松回归要求样本均值等于或者接近样本方差，当二者差异较大时若仍采用泊松回归进行拟合，将导致第一类误差的增加。事实上，高速公路交通事故起数的方差通常远大于其均值，即产生过度离散现象，此时负二项回归模型比泊松回归模型更适合于数据的拟合。负二项分布是一个连续的混合泊松分布，它允许泊松均值服从分布。如果将独立样本表示为Xi，Yi(i=1，2，…，n)，那么Y 的概率分布表达式为

其中Y 为指定地点和指定时段内发生交通事故的随机变量;y 为指定地点和指定时段内预测发生的交通事故起数;μ 为指定地点和指定时段内预测发生的平均事故起数;k 为离散系数，k 值越大，离散性越大。

负二项模型的参数估计可采用最大似然函数法(MLE)来进行，似然函数的形式为

如果以1年为时间间隔来分析高速公路不同路段的交通事故起数，那么建立的单位里程路段年交通事故起数时空分析模型的表达式为

其中λij为第i 个路段第j年的交通事故起数;Qij为第i 个路段第j年的交通量;T 为统计时间，T=365 d;xijk为第i 个路段第j年第k 个自变量;a0、ak为模型参数。

2.2 模型求解与检验

由于不能保证9 个候选自变量对因变量都有显著影响，故本文选用理论上最佳的反向逐步选择法进行时空分析模型自变量的筛选，即先将9 个自变量全部选入方程，然后作F 检验，每一步只剔除方程中偏回归平方和最小(P 值最大)的一个变量，然后对剩余自变量建立新的回归方程。重复上述过程，直至方程中所有自变量都有统计学意义(取显著性水平α=0.05)为止。反向逐步选择法的流程见图1。

本文采用极大似然估计法对模型进行参数估计，即在总体类型已知条件下，某一试验有n 个可能的结果:A1，…，An，当进行试验时，若事件发生了，则认为事件Ai出现的概率最大。定义似然函数为L(θ)，用L(θ)达到最大值去估计θ。

分别采用回归系数的显著性检验、拟合优度检验、AIC 准则(Akaike information criterion) 和 BIC(Bayesian Information Criterion)准则来检验模型的有效性。AIC 准则是一种用于衡量统计模型拟合优良性的方法，该准则借助信息论，按照使AIC 值达到最小来对模型定阶。假设模型误差服从独立正态分布，那么极大似然估计的对数似然函数和相应的AIC 值分别如下式所示，式中p 是模型中待估计的参数个数。

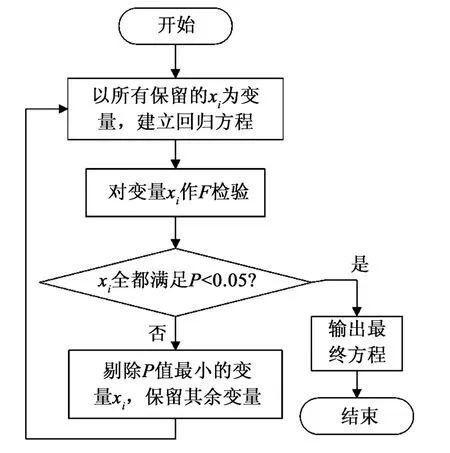
图1 反向逐步选择法流程Fig.1 Flowchart of backward stepwise selection

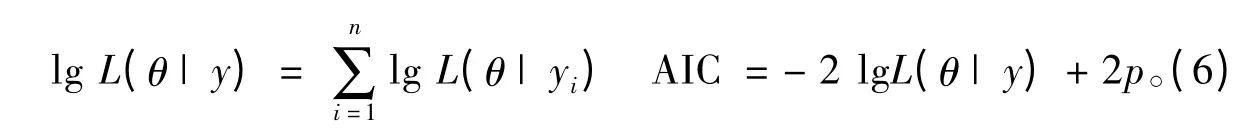
在AIC 准则中，p 取值越小，模型越简洁，AIC 值越小;对数似然函数取值越大，模型越精确，AIC 值越小。因此AIC 准则兼顾了简洁性和精确性，AIC 值越小时，模型拟合程度越好。AIC 准则用于寻找可以最好地解释数据并且包含最少自由参数的模型，但在大样本数据时，由于似然函数值太大，会淹没模型参数p 的影响，此时可以采用BIC 准则，其计算式如下，式中n 为模型中观察值的数量。

BIC 准则考虑了样本数据的影响，由极小化BIC 准则定出的估计值一般要比AIC 得到的估计值更低。在进行回归分析时，BIC 的值越小，其拟合程度越好。

3 实例分析

3.1 模型构建与分析

京港澳高速公路是我国国家级交通运输大动脉，其中粤境北段K39 +180～K52 +180 穿行于崇山峻岭之中，自2003年建成通车至2005年底，该路段共发生481 起交通事故。现以该路段为研究对象，进行高速公路交通事故时空分析模型的实证性研究。由该路段的事故统计数据可得到3年内每起事故发生的时间和地点，测算设计施工图可得到路段的线形指标，另外还可得到每天的分车型交通量。该路段由16 个连续下坡坡段组成，最大纵坡坡度为-4.6%/km，最小圆曲线半径为600 m。采用定长法将其划分为13 个每段1 km 的路段，搜集了连续3年的交通事故纵向数据，共得到474 个有效事故样本点。

将研究路段的事故数据按13 个路段和3 个不同年份进行统计，得到39 个不同路段、不同年份的交通事故起数统计样本，由此计算出该路段交通事故的均值和方差分别为

由上式可知，这段高速公路事故多发段事故起数的方差是其均值的14.67 倍，数据方差远大于均值，数据过离散，因此采用负二项回归来进行拟合在理论上较为合适。

采 用 SAS 软 件 STAT 模 块 的GENMOD 过程［12］对由9 个自变量构建的基于路段长度一致的高速公路交通事故起数负二项回归模型进行数据拟合;本文取显著性水平为0.05，每次剔除一个α ＞0.05 的最不符合的变量，并对剩余变量再次拟合，直至模型中各自变量都有统计学意义为止，最终得到的各变量估计值和检验值见表2。

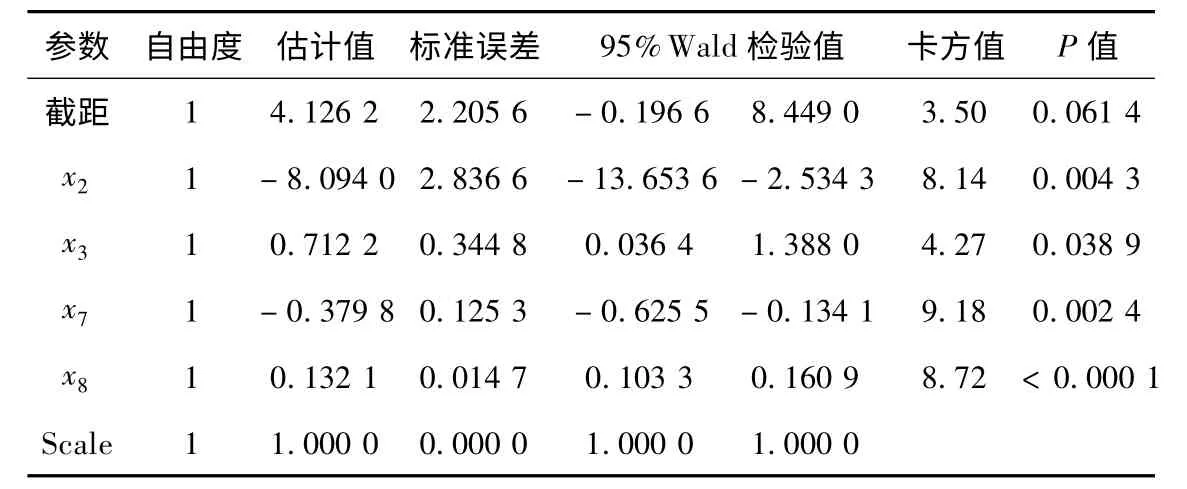
表2 各变量的估计值和检验值Table 2 Estimated values and test values of variables

表2 中各参数的P 值均小于0.05，说明各变量都有显著的统计学意义。将各自变量的估计值带入模型中，得到高速公路交通事故起数负二项回归时空分析模型的表达式如下:

其中x2为大车比例;x3为弯曲比;x7为平均坡度;x8为连续下坡累积效应。

由上式可知，高速公路交通事故率与路段弯曲比、连续下坡累积效应等呈正相关;与平均坡度、大车比例等呈负相关;大车比例是交通事故的首要影响因素，其次是路段弯曲比、平均坡度和连续下坡累积效应。为减少高速公路交通事故，应适当提高车流中的大车比例、减少弯曲路段数量、降低下坡坡度。除大车比例外的其他3 个变量对事故率的影响符合通常思维，无需赘述，故这里仅对大车比例对交通事故的影响做进一步的分析。笔者认为，由于研究对象为货车主导的山区高速公路，其大车比例通常较高，故当小车增多，大车比例下降时，车辆速度差增加，自由度变大，因而发生交通事故的概率增大。

3.2 模型检验

本文采用拟合优度检验模型对样本观测值的拟合程度，SAS 软件给出的拟合优度检验中，异方差为36.137 7，皮尔逊χ2检验值为38.832 1，对数似然检验值为-18.068 9，由此计算出模型的AIC 值为46.1378，BIC 值为44.093 1，说明构建的负二项回归分析模型拟合良好。另外，GENMOD 过程可产生第一类检验和第三类检验，分别为因变量总离差平方和中能解释部分所占的比例(即F 统计量)和各斜率项是否为0 (H0:βj=0)的检验结果。SAS 给出的模型第一类和第三类检验分别见表3 和表4，表中P 值均不超过0.05，表明在α=0.05 的显著水平下，各自变量都有统计意义，即各自变量对高速公路交通事故的影响都是显著的。

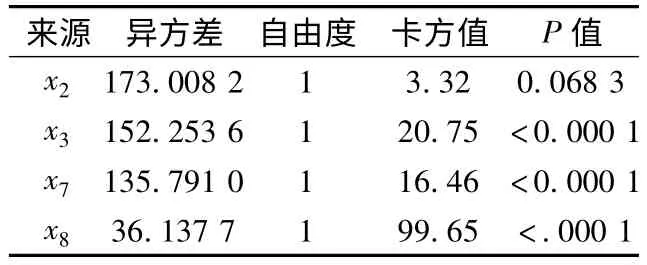
表3 模型的第一类检验分析Table 3 TypeⅠanalysis of the model

表4 模型的第三类检验分析Table 4 Type Ⅲanalysis of the model

4 结语

本文分析了高速公路交通事故的显著影响因素，提出了“连续下坡累积效应”的概念，构建了基于负二项回归的高速公路交通事故时空分析模型，并对京港澳高速粤境北段进行了实证性研究。分析表明，事故率与路段弯曲比和连续下坡累积效应呈正相关，与平均坡度和大车比例呈负相关，大车比例对事故率影响程度最大。该结论适用于我国山区高速公路交通事故的成因分析。由于未能取得车流速度差和天气情况等数据，故本文在建模过程中未予考虑，全面分析高速公路交通事故影响因素还有待于进一步的探讨。

［1］公安部交通管理局.中华人民共和国道路交通事故统计年报(2010年度)［R］.无锡:公安部交通管理科学研究所，2011.

［2］POCH M，MANNERING F.Negative binomial analysis of intersection-accident frequencies［J］.Journal of transportation engineering，1996，122(2):105 -113.

［3］YAN X，RADWAN E，ABDEL-ATY M.Characteristics of rear-end accidents at signalized intersections using multiple logistic regression model［J］.Accident Analysis ＆ Prevention，2005，37(6):983 -995.

［4］WANG X，ABDEL-ATY M.Temporal and spatial analyses of rear-end crashes at signalized intersections［J］.Accident Analysis ＆Prevention，2006，38(6):1137 -1150.

［5］CHANG L Y.Analysis of freeway accident frequencies:Negative binomial regression versus artificial neural network［J］.Safety Science，2005，43(8):541 -557.

［6］张生瑞，马壮林，石强.高速公路隧道群交通事故分布特点及预防对策［J］.长安大学学报:自然科学版，2007，27(1):63 -66.

［7］马明，严新平，吴超仲，等.信号交叉口交通事故频次显著影响因素的作用［J］.吉林大学学报:工学版，2010，40(2):417 -422.

［8］钟连德，孙小端，陈永胜，等.高速公路大、小车速度差与事故率的关系［J］.北京工业大学学报，2007，33(2):185 -188.

［9］周尔波，刘澜.灾害性天气对高速公路交通安全的影响及对策［J］.交通科技，2008，(4):94 -96.

［10］张宏鸣，杨勤科，刘晴蕊，等.基于GIS 的区域坡度坡长因子提取算法［J］.计算机工程，2010，36(9):246 -248.

［11］马壮林.高速公路交通事故时空分析模型及其预防方法［D］.北京:北京交通大学，2010.

［12］SAS Institute Inc.SAS/ STAT 9.2 User＇s Guide The GENMOD Procedure［M］.Cary，NC:SAS Institute Inc，2004.