抵港和装卸时间不确定情况下的离散泊位分配问题
2013-08-29胡志华
谢 鑫,胡志华,2*
(1.上海海事大学 物流研究中心,上海 201306;2.同济大学 经济与管理学院,上海 200092)
近年来,吞吐量的快速增长和集装箱船舶的大型化、高速化给集装箱码头的生产作业带来了巨大的压力.集装箱船舶在港装卸作业量增加,而港口为了提供高质量的服务,必须在承诺的时间内完成船舶的装卸作业任务,但是受泊位资源和装卸资源的限制,时常会出现船舶滞港现象.为了避免这种情况发生,港口最合理的做法就是充分利用现有的资源,提高港口的泊位分配效率和装卸效率.
众多学者已经利用数学规划方法对港口资源的调度进行了研究分析[1-2].采用先来先服务(FCFS)的分配策略,Lai和Shih[3]提出了一种针对泊位分配问题的启发式算法,并利用其对不同分配标准下的分配方案进行了评估.Imai等[4]证明了在多用户集装箱码头系统中,不考虑FCFS原则可以获得较短船舶停泊时间的分配方案以及更高的港口生产力,但是同时也会导致某些船舶等待时间过长,所以他们改进模型追求获得更大的作业效率,同时最小化船舶等待时间.值得注意的是Imai等的研究建立在调度前所有船舶都已抵港的假设基础上,但在实际情况中,船舶都是在调度开始后陆续到港,因此Imai等[5]随后将原有的静态模型发展到动态模型.Nishimura等[6]进一步扩展了动态模型,考虑了不同泊位水深的情形,并设计遗传算法求解模型.Imai等[7]在原有模型的基础上对不同服务优先级船舶的泊位分配问题进行了研究,随后又研究了嵌入式泊位的装卸作业情形.
上述模型和方法大都是面向确定性环境,在这些文献中认为船舶抵港时间和装卸时间是固定不变的并且根据这些确定参数制定泊位分配计划.但是在港口的作业调度中由于存在多种不确定性,如船舶航速变化、天气因素、岸桥机械故障、岸桥效率变化、人员安排变动等原因都会造成船舶抵港时间和装卸时间在原定计划时间上产生波动,如船舶一旦延迟抵港,则按原计划分配的泊位就会产生闲置时间甚至被临时分配给其他船只;而船舶的装卸时间发生波动时,则会影响船舶的离港时间,继而扰乱下一艘船舶的作业计划,因此这使得确定性模型不能正确反映实际系统,甚至会影响最终的分配方案,所以通过确定性模型得出的分配决策过于理想化,不仅达不到优化港口作业的目标,甚至会造成更多地浪费,所以有必要加强面向随机环境的泊位调度研究.Zhou等[8]利用模糊理论对泊位调度中的不确定因素进行了初步探索性研究.Moorthy等[9]基于序列对编码的方法,采用项目评审技术对连续岸线的随机泊位分配问题进行了求解.在国内,周鹏飞等人[10]针对抵港时间和装卸时间的随机性,建立了随机环境下的集装箱码头泊位-岸桥分配模型,并设计了一种改进的遗传算法.而杜玉泉以船舶达到时间具有随机延误和有计划外船舶到港两种不确定性,制定了原始的鲁棒泊位分配方案.
上述有关不确定性环境下的泊位分配研究主要致力于构建具有较强鲁棒性的分配计划,另外有一部分的文献又从干扰管理的角度研究了不确定性环境的泊位调度问题[11-13],但是少有文献研究当船舶抵港和装卸时间发生不同程度波动时,对港口作业目标的影响规律,所以本文针对抵港和装卸时间波动这两种不确定情况,研究它们在不同的波动幅度下对船舶总在港时间产生的影响规律.
1 问题描述
泊位调度分为离散泊位调度和连续泊位调度.连续泊位调度将整个码头岸线看作是连续的,只要有满足到港船舶物理条件(水深和长度)限制的位置就可以进行停泊.而离散泊位调度是将码头岸线划分为若干独立的泊位来进行分配.本文的研究是基于离散泊位调度环境.
离散泊位调度指的是,在一条被分为I个泊位的岸线上,为每一条到港的船舶分配一个合适的停靠泊位和停靠时间[14].一般制约泊位分配的因素主要有:1)船舶有关信息,如船期计划、船长、吨位、装卸量等.2)岸边资源情况,如岸桥、集卡调度等.3)其他物理条件,如泊位长度、水深等.
可是港口运作中有许多不确定因素,按照其来源可以分为来自系统外的不确定性和正常生产中的不确定性两类.
来自系统外的不确定性是指,码头生产受到来自整个运输链上下环节的制约和影响,这些因素难以确定是动态变化的,另外船舶的航行速度也会动态变化,这些发生在港口系统外部的不确定因素直接导致了船舶抵港时间的波动.而正常生产中的不确定性表现在生产过程中由于人为操作或设备间等待、干扰而产生的作业效率和处理能力的不确定性.如:岸桥干扰、机械故障、人员安排变动.这些因素直接导致了船舶装卸时间的波动.
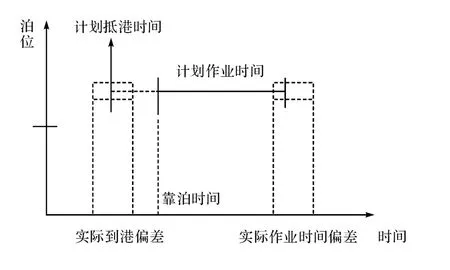
图1 抵港时间和装卸时间偏差示意图Fig.1 Schematic diagram of arrival and handling time deviation
船舶航速变化、天气因素、岸桥机械故障、岸桥效率变化、人员安排变动等不确定因素,根据其不确定性的强度,使船舶的抵港和装卸时间产生不同程度的波动,如图1所示.根据波动程度的不同,必然会对原计划产生不同的影响.在不同的波动幅度下到底会对港口的作业目标(本文考虑最小化船舶总在港时间)产生怎样的影响,接下来本文就分别用静态数据和产生波动的数据计算船舶的总在港时间并进行比较.
2 动态泊位分配模型
在本文中泊位分配模型将基于以下前提:1)船舶到港时间作为随机变量来考虑;2)船舶装卸时间将根据泊位、岸桥等因素确定,属于随机变量;3)不考虑移泊情况,每个船舶只有一次靠泊机会;4)考虑船舶物理特性与水深对分配计划的约束.5)船靠泊后立刻进行装卸作业,不考虑等待岸桥时间.
2.1 模型
B,V,U为模型中考虑的泊位集、到港船舶集和船舶服务顺序集,i=(1,2,…,I)∈B,j=(1,2,…,T)∈V,k=(1,2,…,T)∈U.
当船舶j在Aj时刻到达港口时,港口工作人员根据船舶的长度Lj和设计吃水深Dj选择合适靠泊泊位i,即泊位i、长度Li和水深Di均大于Lj和Dj,如果没有合适的泊位则船舶j在锚地等待.一旦有合适的泊位i分配给船舶j,则船舶靠泊,此时在船舶j前有k-1艘船进行了装卸作业,船舶j在bijk时刻开始在泊位i第k个进行装卸任务,经过装卸时间Cij后在时刻fijk结束作业,然后离港.以下为相关符号的定义:
M:大型常数;Aj:船j到港时间;Cij:船j在泊位i的装卸作业时间;bijk:船j在泊位i第k个服务的开始装卸作业时间;fijk:船j在泊位i第k个服务的结束作业时间;Di:泊位i的水深;Li:泊位i的长度;Dj:船j的设计吃水深;Lj:船j的长度.Xijk=1,表示船j在泊位i第k个被服务;否则,Xijk=0.Xvijk:当船j在i泊位第k个被服务时的总在港时间;Xijk,bijk,Xvijk,fijk为决策变量.
数学模型:
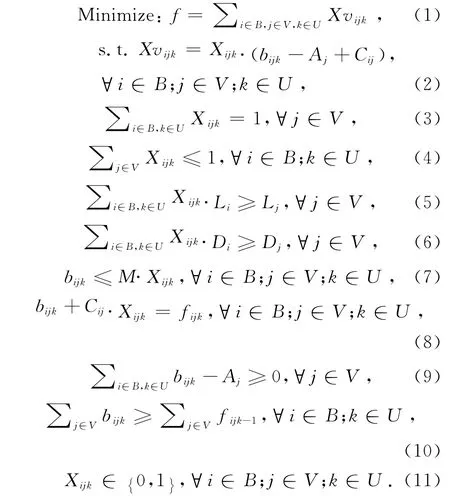
该数学模型的优化目标是所有船舶总在港时间最小化.式(2)定义了Xvijk与bijk、Aj、Cij、Xijk之间的关系,表示船舶总在港时间等于船舶抵港到开始装卸作业的时间与装卸时间之和.约束(3)表示所有船舶有且只有一次靠泊机会.约束(4)保证泊位上同时停泊的船舶不超过1艘.约束(5)和(6)给出了泊位对于船舶长度和水深的约束条件.约束(7)保证当Xijk=0时,bijk=0,否则bijk≥0.式(8)给出了船舶开始作业时间、装卸时间和作业结束时间之间的关系.约束(9)保证船舶到港后才能被服务.约束(10)保证在某一泊位被服务的船舶作业开始时间大于该泊位前一艘船的结束作业时间.式(11)声明决策变量Xijk是0~1变量.
“互联网+”教育深入融合的当今时代,微课等形式作为新的教学模式在教学课堂中如火如荼进行着。为解决成人继续教育学员的工学时间矛盾的突出问题,提高教学效果和学员的学习质量为教学目标,我们将微课理念融入继续教育课程建设中,我们尝试在“C语言程序设计”这门课的继续教育中引入微课为基础的翻转课堂教学,探究其在“C语言程序设计”中的应用效果。
由于式(2)是非线性的,为了方便该数学模型采用Cplex工具求解,这里将式(2)转换为线性约束(12):
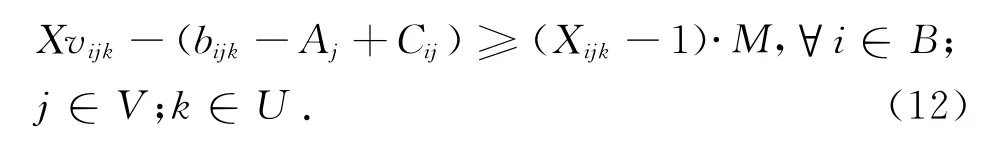
2.2 抵港和装卸时间的不确定性处理
2.2.1 集装箱码头船舶到港规律 在集装箱运输出现之前的海上货物运输,主要是以散装货运输为主,这种运输模式下的船舶到港时间间隔分布规律基本是随机的.国内外学者通过大量到港船舶时间的数理统计的研究,通常认为单位时间内到港船舶数服从泊松分布,而到港时间间隔服从负指数分布.但是集装箱运输自出现开始得到快速发展,且主要是班轮化运输,有固定的航线、船期、挂靠港口.这种运输模式显然与散装货运输的随机性是不同的,因此再用原来的计算方法就不是很合理.
根据张鲁宁,王诺等[15]对集装箱班轮到港规律的实证研究,认为船舶的到港规律更符合爱尔朗分布.爱尔朗分布函数如式(12)所示.
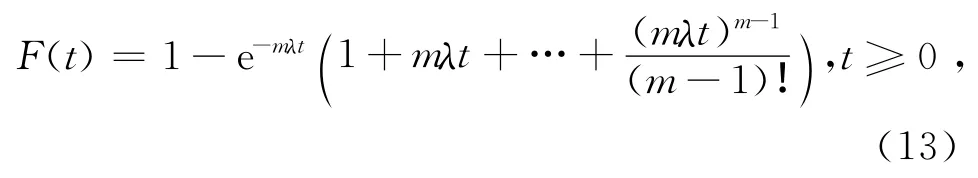
其中,当m=1时,其分布就是负指数分布,不定期的杂货船到港规律就服从该分布;当m→+∞,即集装箱船舶到港规律在理想状态下服从的分布.在本文中取m=2,即到港时间间隔服从二阶爱尔朗分布,得到式(13),其中1/λ为到港时间间隔的期望值.
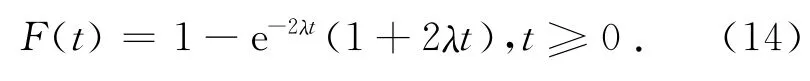
2.2.2 船舶计划抵港时间和计划装卸时间 本文设定第一艘船的到港时间为0∶00点,则后面的船舶到港时间可以根据到港时间间隔规律的分布,通过式Aj+1=Aj+Tj+1,j(其中Tj+1,j为船舶到港时间间隔)随机生成12艘船的计划到港时间.船舶的计划装卸作业时间由U(1,3)* (船舶长度)Lj/40随机生成.
2.2.3 抵港和装卸时间的不确定性处理 由于船舶航速变化、天气因素、岸桥机械故障、岸桥作业效率变化、人事安排变动等外部因素都会造成船舶抵港时间和装卸时间在原有计划时间上产生波动,因此要考虑这一部分对模型数据造成的影响.根据统计分析,船舶的实际抵港时间和装卸时间与计划时间之间的偏差可以认为是服从正态分布的,偏差量为期望值为零的正态分布随机变量,我们可以为偏差量设定不同的均方差来表示外界环境对于计划时间产生的波动程度.所以本文偏差量服从正态分布N(0,σ2),根据波动程度的大小,在轻度波动下σ2在区间[1,2]上随机生成,中度波动下在区间[2,3]上随机生成,高度波动下在区间[3,4]上随机生成(都服从均匀分布).
3 算例
本文中选取了4个泊位和12艘船设计算例,以评价和测试建立的模型.泊位长度、水深以及船舶的长度、设计水深都是在一定的范围内服从均匀分布.泊位信息列于表1,船舶信息列于表2.
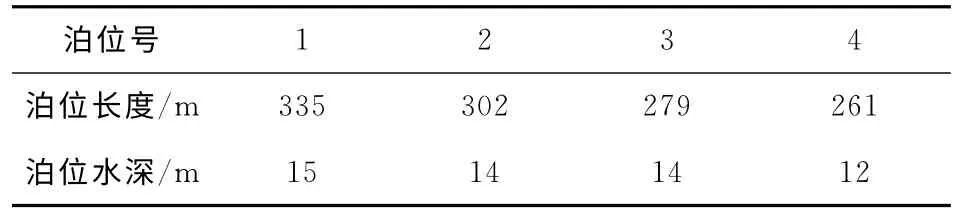
表1 泊位信息Tab.1 The information of berths
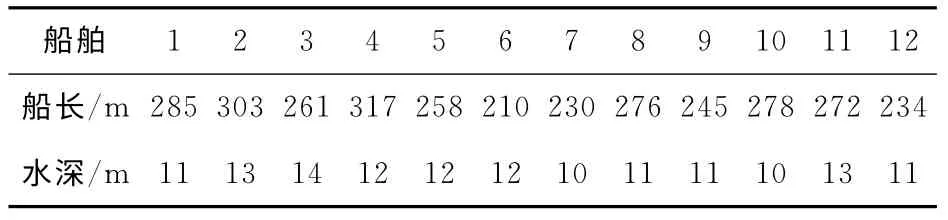
表2 船舶信息Tab.2 The information of vessels
首先随机生成某一到港时间间隔下的船舶计划抵港时间和计划装卸时间,得出计划目标值(船舶总在港时间);然后在装卸时间不变的情况下,对计划抵港时间进行不同波动模式下的处理,即(实际抵港时间)^Aj=(计划抵港时间)Aj+(偏差量)α,为了使得到的数据更加稳定,对目标值生成多组数据,然后相加求平均值.图2为不同时间间隔下,计划目标值和3种抵港时间波动模式下的目标值.图3为3种波动模式产生的目标值与计划值的偏差幅度.
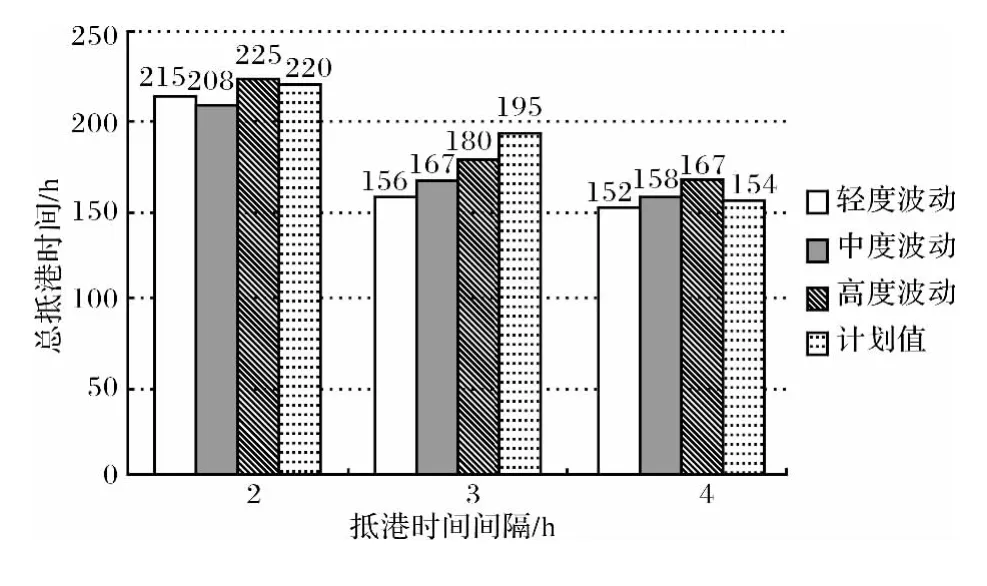
图2 不同抵港时间波动下船舶总在港时间Fig.2 The planned and actual target value under different degrees of arrival fluctuation
分析图2,船舶的总在港时间随着抵港时间间隔的扩大而下降,这是符合实际情况的,因为当抵港时间间隔扩大时,单位时间内到港船舶减少,使现有的泊位资源和装卸资源变得相对充裕,需要处理的信息也减少,加快了船舶的过关效率.结合图3分析船舶总在港时间的波动范围,可以看到当平均间隔为2h 时目标值分布在区间[208,225]之间,偏差幅度分别为2%、5%和2%,4h时目标值分布在区间[152,167]之间,偏差幅度分别为1%、3%和8%,偏差比较小,但是当平均间隔为3h时,目标值分布在区间[156,194]之间,偏差幅度分别为20%、15%和8%,偏差表现得就比较明显.
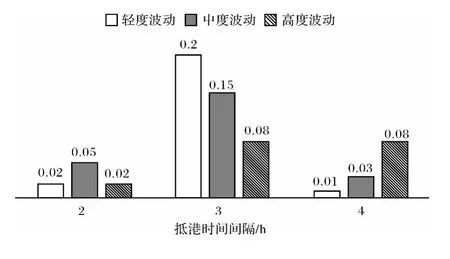
图3 不同抵港时间波动下船舶总在港时间与计划值的偏差幅度Fig.3 Deviation amplitude between the planned and actual target value under different degrees of arrival fluctuation
然后在船舶抵港时间不变的情况下,对装卸时间进行波动的处理并计算目标值,图4为计划目标值和3种装卸时间波动模式下的目标值,图5为3种波动模式下产生的目标值与计划值的偏差幅度.
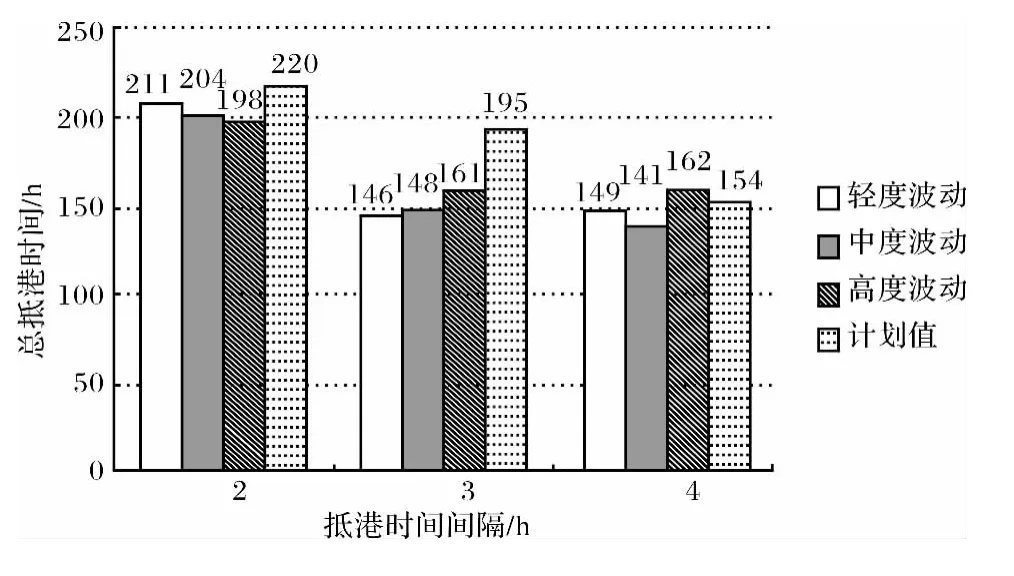
图4 不同装卸时间波动下船舶总在港时间Fig.4 The planned and actual target value under different degrees of handling fluctuation
分析图4和图5,图中呈现的规律与图2和图3相似,都表现为平均间隔为2h和4h时的偏差要小于平均间隔为3h时的偏差.但是对比图3、图5可以发现发生在岸桥上的波动产生的目标值相较于计划值的偏差要大于由于抵港时间波动所产生的偏差.如当平均时间间隔为2h时,波动产生的目标值与计划值分布在区间[198,220],偏差幅度分别为4%、7%和10%,要大于同一情况下由于抵港时间波动而产生的偏差幅度2%、5%和2%.另外观察这两张图,可以发现一个有趣的地方,就是用考虑波动后的数据运用模型计算出来的目标值相较于计划值都有一定的改善,这说明采用静态数据生成的泊位分配计划就船舶总在港时间上来说在实际港口作业中往往不是最优的,一旦发生波动,新的泊位分配方案可以获得更优的目标值.因此如果决策者要为某段时间制定一个考核目标,比如说总在港时间,如果根据静态数据来制定的话是不合理的,而应该在计划值的基础上提高考核要求.
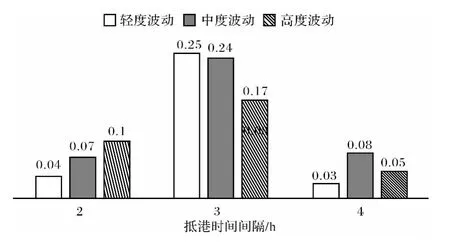
图5 不同装卸时间波动下船舶总在港时间与计划值的偏差幅度Fig.5 Deviation amplitude between the planned and ctual target value under different degrees of handling fluctuation
4 结论
在集装箱码头的泊位分配中,由于船舶航速变化、天气因素、岸桥机械故障、岸桥效率变化、人员安排变动等原因,船舶抵港和装卸时间具有明显的动态性,会产生不同程度的波动.本文针对离散泊位建立动态泊位分配模型,采用Cples求解,对静态数据进行了波动处理来研究抵港时间和装卸时间的波动对船舶总在港时间的影响.结论表明在船舶抵港时间间隔为3h时,抵港和装卸时间波动造成的总在港时间与原目标的偏差幅度大于间隔为2h和4h的情况,并且随着波动程度的升高这种差距减小;由于装卸时间的波动产生的总在港时间偏差比抵港时间波动产生的偏差更为明显.
本文还存在不足,首先模型中目标函数的评价指标单一,只考虑了时间因素,因此在设定泊位调度优化目标时可以考虑最小化船舶离港比计划离港时间延迟程度以及靠泊泊位与偏好泊位偏离程度等.其次由于本文中没有考虑先到先服务原则,导致有些船舶的等待时间过长,可以考虑为每艘船设定最大等待时间.但在实际过程中可能不能满足所有船的等待要求,所以可以再设定船舶满足等待时间的保证率,这一点可以在模型中增加相应的约束条件来实现.
从实验数据中可以看出,当抵港时间和装卸时间发生波动时,对泊位分配影响是很大的,所以需要考虑加入一个缓冲时间来减小抵港延误和装卸延误的影响,如何制定缓冲时间的长短使得抵港和装卸时间波动产生的影响最小,又能保证港口较高的运作能力是本文以后继续研究的方向.
[1]Bierwirth C,Meisel F.A survey of berth allocation and quay crane scheduling problems in container terminals[J].European Journal of Operational Research,2010,202(3):615-627.
[2]韩晓龙,丁以中.集装箱港口装卸作业仿真系统[J].系统仿真学报,2006,18(8):2366-2369.
[3]Lai K K,Shik K.A study of container berth allocation[J].Journal of Advanced Transportation,1992,26(1):45-60.
[4]Imai A,Nagaiwa K,Chan W T.Efficient planning of berth allocation for container terminals in Asia[J].Journal of Advanced Transportation,1997,31(1):75-94.
[5]Imai A,Nishimura E,Papadimitriou S.The dynamic berth allocation problem for a container port[J].Transportation Research Part B,2001,35(4):401-417.
[6]Nishimura E,Imai A.Berth allocation planning in the public berth system by genetic algorithms[J].European Journal of Operational Research,2001,131(2):282-292.
[7]Imai A,Nishimura E.Berth allocation at indented berths for mega-containerships[J].European Journal of Operational Research,2007,179(2):579-593.
[8]Hao J,Shi L,Zhou J.An ant system algorithm with random perturbation behavior for complex TSP problem[J].Systems Engineering—Theory &Practice,2002,25(9):88-91.
[9]Moorthy R.Berth management in container terminal:the template design problem[J].OR Spectrum,2006,28(4):495-518.
[10]周鹏飞.面向随机环境的集装箱码头泊位-岸桥分配方法[J].系统工程理论与实践,2008(1):161-169.
[11]杨春霞,王 诺.集装箱码头泊位分配干扰管理决策方法研究[J].运筹与管理,2011,20(4):90-95.
[12]曾庆成,胡祥培.集装箱码头泊位分配-装卸桥调度干扰管理模 型[J].系 统 工 程 理 论 与 实 践,2010,30(11):2026-2035.
[13]Zhen L,Lee L H,Chew E P.A decision model for berth allocation under uncertainty[J].European Journal of Operational Research,2011,212(1):54-68.
[14]Buhrkal K,Zuglian S,Ropke S.Models for the discrete berth allocation problem:A computational comparison[J].Transportation Research Part E,2011,47(4):461-473.
[15]张鲁宁,王 诺.集装箱班轮到港规律实证研究[J].大连海事大学学报,2012,38(1):47-48.
