T形和Π形电阻电路等效变换的教学探讨

田社平，孙 盾，张 峰

(1上海交通大学电子信息与电气工程学院，上海 200240;2浙江大学电气工程学院，浙江杭州 310027)

T形和Π形电路在工程实践中具有广泛的应用，如三相电路中的星形连接和三角形连接、滤波电路中双T形滤波等。等效变换是电路理论中的一种重要的常用分析方法。因此，T形和Π形电路的等效变换是电路教学中一项非常重要的内容。几乎所有的“电路理论”或“电路分析”教材中都包含这一内容。笔者在教学中发现，可以从不同的角度来看待T形和Π形电路的等效变换关系，其等效变换公式的推导也可从不同的角度来加以展开。下面根据笔者的教学实践，试对这一问题作一分析，并给出这一内容的教学建议。

通过电路等效的定义，可以推导出T形和Π形电路的等效变换公式。但在具体推导过程中，则可从不同角度来理解电路等效的定义，从而得到不同的推导过程。

1 基于等效定义的推导方法

如果端钮一一对应的n端口电路N1和N2具有相同的端口特性，即相同的两组端口电压分别代入两个电路的端口特性方程会得出相同的两组端口电流，或者将相同的两组端口电流代入两个电路的端口特性方程会得出相同的两组端口电压，则二者相互等效，并互称等效电路。基于这一定义，即可推导T形和Π形电路的等效变换公式。国内许多教材都遵循了这一思路［1～5］。为便于比较，下面将推导过程简列如下。

对图1(a)所示的电路，取节点③为参考节点，可列出该三端电路的端口特性所满足的方程为同样，可列出图1(b)所示电路的端口特性所满足的方程为

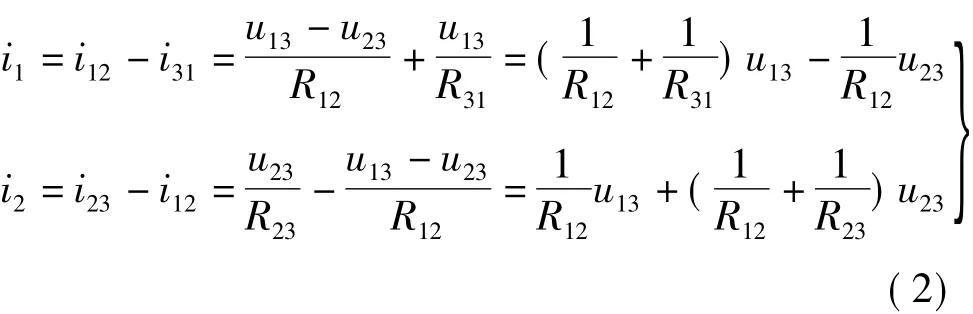
图1 T形电路和Π形电路

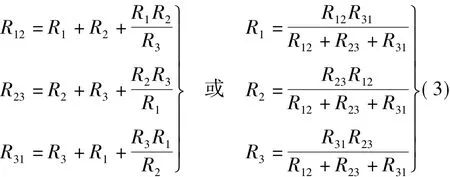
显然，当式(1)和式(2)的系数矩阵互为逆矩阵时，两式所表示的端口特性完全相同。由此条件可求得T形电路和Π形电路的等效变换公式为

2 基于等效性质的推导方法

由电路等效的定义，可以得到电路等效的一个性质:如果两个电路等效，则在两个电路的某一或某几个端口连接相同的任意电路，则得到的两个新的电路也是相互等效的。利用这一性质，可以得到推导T形和Π形电路等效变换公式的一些简单而有趣的方法。

端口外接电路的最简单的情况就是开路和短路［6］。将图1(a)和(b)两个电路的②、③端开路，则从①、③端看进去的等效电阻应相等，即

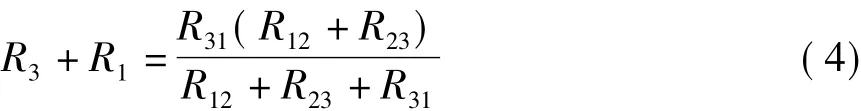
类似地，可以得到

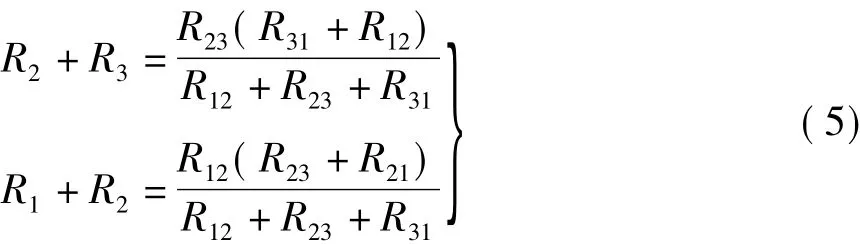
联立求解式(4)和式(5)，就可以得到与式(3)相同的T形电路和Π形电路的等效变换公式。

如果将图1(a)和(b)两个电路的②、③端短路，则从①、③端看进去的等效电阻也应相等，利用这一性质同样可以得到与式(3)相同的T形电路和Π形电路的等效变换公式。

利用电路等效的性质，还可以衍生出多种分析方法。这里仅举一例。将图1(a)和(b)两个电路分别端接如下电路:②和③端连接电阻R23;①和③端连接电阻R31;①和②端连接电阻R12，则可以得到

求解式(6)，就可以得到与式(3)相同的T形电路和Π形电路的等效变换公式。

3 基于能量守恒定律的推导方法

能量守恒定律是物理系统包括电路都必须遵守的普遍规律，如果两个电路等效，则对相同的端电压和端电流，两电路消耗的能量相同。

在图1中已标出端电流i1，i2，i3，它们满足i1+i2+i3=0。对T形电路，其消耗的功率为

对Π形电路，其消耗的功率为

为求出电流i12，列写KVL方程，得

解得

令 pT=pΠ，并将式(10)代入整理，得

由于i1和i2可取任意值，因此有

由上式就可以得到与式(3)相同的T形电路和Π形电路的等效变换公式。

4 基于戴维南定理的推导方法

在图1(a)和(b)两个电路的②、③端分别连接一电压为uS的电压源。由于两电路等效，因此从两个电路的①、③端看进去的戴维南等效电路相同，即两者的开路电压uOC、等效电阻Ro分别相等，于是可以得到

由上式可得

式(14)和(15)中的四个等式只有三个是相互独立的，利用其中任意三者即可得到与式(4)相同的T形电路和Π形电路的等效变换公式。

5 基于二端口参数矩阵的推导方法

三端电路可以构成二端口电路。如果将图1所示T形电路和Π形电路的端钮①、③和②、③分别看作一个端口，则T形电路的r参数矩阵为

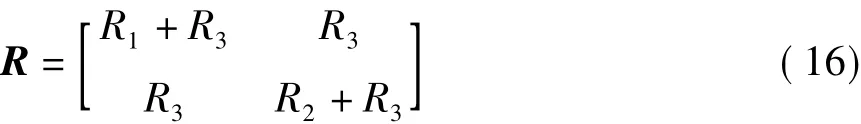
Π形电路的g参数矩阵为

两电路等效，则有R-1=G或R=G-1，由此即可得到与式(3)相同的T形电路和Π形电路的等效变换公式。

6 教学建议

由上面的分析可以看出，T形电路和Π形电路的等效变换与电路理论的许多知识点相关联，这也反映了电路理论的概念、原理和方法的内在联系。这些知识点包括:功率守恒、KCL、KVL、等效变换、开路与短路、串并联、戴维南/诺顿定理、二端口电路等。以T形电路和Π形电路的等效变换为中心，在教学中将这些知识点串连起来，可以提高教学效果。我们建议采用如下几种教学形式:

(1)课堂教学—方法1和方法2比较适合在课堂上讲授，这两种方法与等效电路的定义最为直接。笔者教学所使用的教材［1］中采用的是方法1，而课堂教学时采用的是方法2。

其他方法如果要在课堂上讲授，则将其作为例子引入较为合适。例如，在讲授戴维南/诺顿定理时，可以引入运用戴维南/诺顿定理推导T形电路和Π形电路等效变换公式的例子。

(2)课堂讨论—在进行T形电路和Π形电路等效变换教学时，可以采用讨论式教学的形式。此时方法1～3均属于讨论的范围(方法4～5的知识点为后续教学内容)。讨论的议题包括三个方面:等效公式的推导方法;等效电路定义的内涵;KCL、KVL与能量守恒定律关系的再认识。笔者认为讨论的过程必须由教师加以引导，对讨论中提出的问题进行提示和解释，方可取得良好的效果。

(3)课外研讨—在笔者的教学中，一直设置了分组课外研讨并撰写小论文的环节，笔者曾公布“T形电路和Π形电路等效变换”的选题，得到了学生的热烈响应。一部分学生通过查阅文献、独立思考和相互交流，提出了自己的看法。

［1］ 陈洪亮，张峰，田社平.电路基础［M］.北京:高等教育出版社.2007

［2］ 陈希有.电路理论基础［M］，第二版.北京:高等教育出版社，2004

［3］ 李瀚荪.简明电路分析基础［M］.北京:高等教育出版社.2002

［4］ 于歆杰，朱桂萍，陆文娟.电路原理［M］.北京:清华大学出版社，2007

［5］ 邱关源.电路［M］，第四版，北京:高等教育出版社，1999

［6］ J.W.Nilsson，S.A.Riedel.Electric Circuits［M］，seventh edition，New York:Prentice Hall，2005