CGFRP 材料加固圆管受压柱稳定承载力分析

殷保方 何 琦 夏红玲

(1.重庆交通大学土木建筑学院，重庆 400074;2.中国兵器长安工业，重庆 401120)

0 引言

纤维增强复合材料(Fiber Reinforced Plastic，简称FRP)具有轻质高强、耐腐蚀性好、弹性性能好、绝缘、隔热、施工便捷、便于维护等优点，因此被广泛应用于土木工程加固领域。近年来FRP材料加固钢筋混凝土及木结构的理论已经比较成熟，但对FRP加固钢结构的理论和实验研究相对较少。

本文通过建立“壳元—弹簧单元—壳元”模型，对轴心受压圆管柱粘贴CGFRP加固后的承载力性能进行了分析，并对影响参数进行讨论。此外为了使此类构件承载力计算更简便、实用性更强，提出简化计算模型并采用Perry公式计算其承载力，将计算结果与有限元结果进行对比、分析、修正，并且给出修正系数ω的曲线拟合公式，对于工程上估算、设计、补强同类构件具有一定的参考意义。

1 CGFRP加固方案

模拟试验采用圆管柱试件，截面形式如图1所示，柱的长度均为1 500 mm，长细比均在100以内。首先，为了防止圆管钢柱与碳纤维布发生电离，在钢柱表面环向包裹一层玻璃纤维布，其纤维长度方向与钢柱轴向一致，然后在粘贴好的玻璃纤维布上粘贴碳纤维布，碳纤维长度方向与玻璃纤维相同。钢柱与玻璃纤维布及玻璃纤维布与碳纤维布的表面之间用环氧树脂粘结。

图1 截面形状（单位：mm）

2 模型建立

2.1 CGFRP的力学性能指标

模拟试验中的加固材料不是单纯的一种FRP材料，而是由碳纤维复合材料(CFRP)和玻璃纤维复合材料(GFRP)通过湿作业法有效结合在一起，形成的CGFRP混合纤维复合材料，这种由两种纤维增强材料复合而成的材料其性能会与单一FRP材料有很大区别。碳纤维和玻璃纤维混杂复合而成的CGFRP的应力—应变关系呈非线性(见图2)。

CGFRP在拉应力的作用下，延伸率较低的CFRP首先破坏，形成裂纹，由抑制裂纹增长理论可知，高延伸率的GFRP起到抑制裂纹扩展的作用，并承受由CFRP断裂后而引起的额外荷载。此外CFRP断裂成短纤维后仍能在刚度和强度上发挥不小的作用。可将CGFRP的应力应变关系分为两个阶段，第一阶段为碳纤维断裂之前，第二阶段为碳纤维断裂之后。

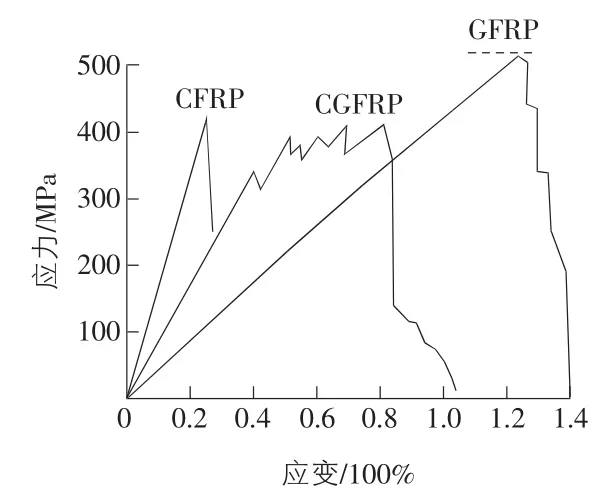
图2 典型的应力—应变曲线

由混杂定则得到:

第一阶段的弹性模量:

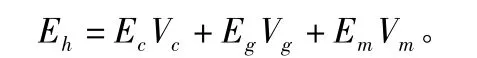
第二阶段的弹性模量:

第一次断裂的强度:

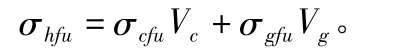
第二次断裂的强度:

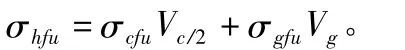
本次模拟试验CGFRP材料属性如表1所示。

表1 CGFRP材料属性表

2.2 单元选取

本文选用ANSYS有限元计算软件建立“壳元—弹簧单元—壳元”模型，即圆管钢柱和CGFRP层都采用壳单元，环氧树脂胶结层采用弹簧单元。

模型单元界面简图如图3，图4所示。

钢柱—Shell181壳单元，胶层—Combine14弹簧单元，CGFRP层—Shell63壳单元。为防止钢柱顶端直接承受荷载，发生局部屈服，故需在钢柱顶端设置刚度较大的端板，使用Solid73实体单元进行模拟。

3 结果分析

3.1 试验结论

图3 节点位置关系图

图4 “壳—弹簧—壳”模型

由图6上CGFRP层的应力比图5上CGFRP应力大的多可知，初始弯曲率越大的构件受到的加固效果越显著，而CGFRP对初始弯曲率较小的构件的稳定承载能力基本没有增强效果。比较分析曲线图7～图10的变化规律可看出:CGFRP对轴心受压圆管钢柱的稳定承载能力的增强效果较明显，尤其是对初始弯曲率大、宽厚比大的构件增强效果更为显著，而加大CGFRP层的厚度对构件的承载力增强效果基本无太大影响。

图5 初始弯曲1/2 000时CGFRP应力图

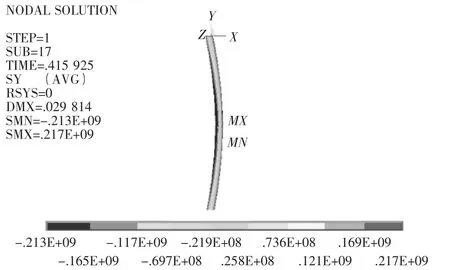
图6 初始弯曲1/500时CGFRP应力图

3.2 原因分析

初始弯曲实质上是改变了构件的受力模式，由轴心受压变为偏心受压，初始弯曲越大构件边缘越容易发生局部屈服，导致失稳破坏，处于受拉区的CGFRP将承受更多的拉应力，加固效果更显著。由混杂效应计算结果知，CGFRP层越厚，其极限应变越小，CGFRP纤维将在钢柱体外边缘钢纤维发生屈服之前出现脆性破坏，导致CGFRP提前退出工作。故增加CGFRP层的厚度未必会大幅度提高轴心受压圆管柱承载力。

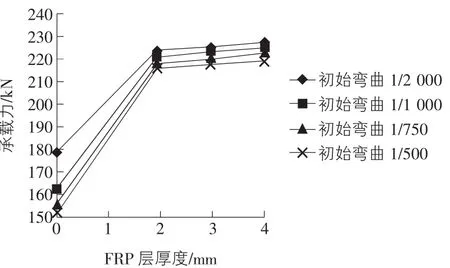
图7 CGFRP厚度—承载力关系图

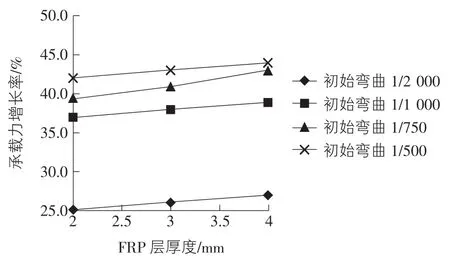
图8 CGFRP厚度—承载力增长率关系图

图9 圆管截面厚度—承载力关系图

图10 钢柱截面厚度—承载力增强率图

4 简化计算模型

ANSYS有限元模型中胶结层(环氧树脂)的主要作用是有效粘结玻璃纤维布与碳纤维布及钢柱表面与玻璃纤维布。由于钢材与环氧树脂之间的粘结力非常复杂，很难在理论计算中将胶结层的作用考虑进去;此外，胶结层非常薄，而且弹性模量相对于钢柱体和CGFRP层来说非常小，在理论计算中可以忽略不计胶结层对构件截面的抗拉和抗弯刚度的影响;故本文提出的理论简化计算模型中忽略了胶结层的影响，将CGFRP加固圆管轴心受压钢柱ANSYS有限元模型简化成如图11所示的等效简化模型。

本文拟用Perry形式的稳定系数公式计算构件稳定承载力，其形式为:

图11 简化模型截面图（单位：mm）

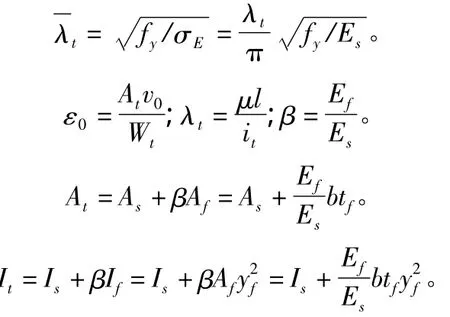
从表2及图12可看出有限元结果和Perry计算结果存在差异。这是由两个方面原因造成的:

首先，Perry公式采用的是简化模型，忽略胶层的影响，即认为FRP层直接作用在钢柱表面，二者无相对滑动，因此Perry公式计算结果会明显偏大;

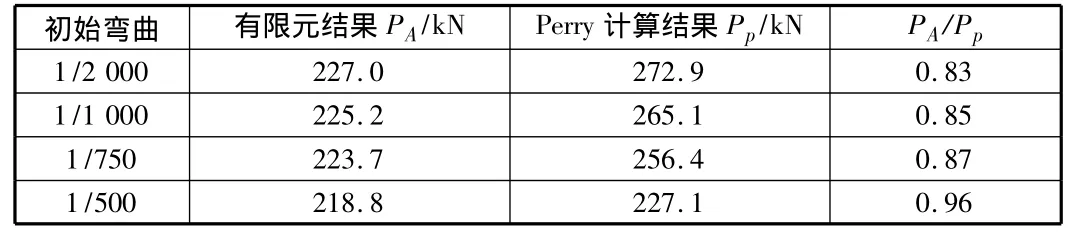
表2 不同初始弯曲下构件承载力对比表

图12 承载力—初始弯曲关系图

其次，Perry公式是由构件截面边缘屈服准则推导出的，求得的临界应力为边缘受压纤维达到屈服时的最大应力，而不是稳定临界应力，实质上是用强度的应力问题代替稳定问题，故所得结果相对偏于保守。

两方面原因综合作用使得简化模型计算结果和有限元结果出现明显差异。为了保证计算结果的准确性，需根据ANSYS分析结果对Perry公式计算结果进行修正。

修正系数:

与图13中拟合曲线对应的拟合公式为:ω =55 896v2－52.29v+0.844。

图13 初始弯曲—修正系数关系图

5 结论与建议

1)由于混杂效应的影响，CFRP和GFRP复合而成的CGFRP材料断裂伸长率、强度等优于单一FRP材料。对结构加固领域材料的选用起到一定参考作用。

2)粘贴FRP对轴心受压构件的承载力增强效果明显，尤其是对初始弯曲大、宽厚比大的构件，而增加FRP层厚度对构件承载力的增强效果则差强人意。

3)提出一个简化的等效截面计算模型，用Perry公式计算构件的承载力，根据有限元分析结果对简化模型计算结果进行修正，提出了一个承载力修正系数ω以及ω的拟合公式。此等效模型及相应的理论计算公式计算简便，有一定的可靠性，对加固同类构件具有一定参考意义。

［1］ 王助成，邵 敏.有限单元法基本原理和数值方法［M］.北京:清华大学出版社，1997.

［2］ ANSYS Theory Refernce.Electronic Release.SAS IP Inc.，1998.

［3］ 王震鸣，杜善义，张 恒，等.复合材料及其结构的力学［M］.北京:北京大学出版社，1998.

［4］ 曾庆敦.复合材料的细观破坏机制与强度［M］.北京:科学出版社，2002.

［5］ 张绪平，丁克伟.CFRP片材加固钢梁的有限元分析［J］.安徽建筑工业学院学报(自然科学版)，2009，17(2):14-17.

［6］ Ziraba Y N，Baluch M H，Basunbul I A，et al.Guide-lines toward the design of reinforced concrete beams with externally bonded composite laminates［J］.ACIStructural Journal，1999，96(2):212-220.