复合加载下6自由度圆形基础的极限承载力

张其一，张 颖，王 琦

(1.中国海洋大学工程学院，山东 青岛 266100;2.山东省海洋工程重点试验室，山东 青岛 266100)

水利、港口、海洋工程以及工业与民用建筑物除了受到自身长期的竖向荷载作用外，往往还会遭受到波浪、水流、暴风等引起的瞬时或循环的水平荷载和力矩荷载的作用.这些荷载通过基础传到地基上，导致地基土体同时受到竖向荷载、水平荷载和力矩荷载的共同作用，地基的这种受力模式称为复合加载模式［1－2］.复合加载模式下地基土体的失效机理目前尚不十分明确，国内外学者主要采用土体破坏包络面的方法求解复合加载模式下地基的极限承载能力［3－4］.所谓地基破坏包络面是指在水平荷载、竖向荷载以及力矩荷载的共同作用下，地基土体达到整体平衡时，荷载分量在荷载空间中形成的一个外凸曲面.在V－H，V－M，H－M两维荷载空间以及V－H－M三维荷载空间中，国内外学者M.F.Bransby［5］，B.Ukritchon［6］，H.A.Taiebat［7］，S.Gourvenec［8］以及栾茂田［9］等人对其进行了大量的数值研究，给出了大量的经验计算公式，对多自由度情况下地基土体的极限承载能力计算奠定了基础.

本研究基于土体极限平衡理论，以海洋平台圆形基础为研究对象，采用有限元数值计算方法，对6自由度荷载空间中地基土体的极限承载能力进行较为细致的研究.拟给出复合加载模式下圆形基础达到极限平衡状态时的破坏包络面方程和海床土体的破坏模式，用数值计算结果对上述公式进行验证.

1 数值分析

1.1 数值计算模型

本研究采用的数学模型如图1所示.

图1 6自由度圆形基础模型

图1 中，V，Hx，Hy，Mx，My和 T 分别为坐标轴方向上的集中力荷载和力矩荷载.

假定直径为D的刚性圆形基础作用在不排水饱和软黏土海床上，土体采用基于Mohr-Coulomb破坏准则的理想弹塑性模型，基础和地基土体间假定为完全黏结，且无脱离接触现象.为减少有限元计算过程中地基模型的边界效应，海床土体取为圆柱形，直径和深度均取10D;土体表层为透水边界，其余边界均为不透水边界.海床地基包括26800个二阶减缩积分单元，圆形基础用无限刚度的刚体模拟.有限元数值计算模型如图2所示.

不排水饱和软黏土黏聚力与内摩擦角分别取Su=12 kPa和φ=0°，弹性模量和泊松比分别取为E=5.8 MPa与 ν=0.49，海床土体中地应力系数按照Jaky公式取1.0.针对海床土体不排水饱和软黏土体积不可压缩的特性，采用了2阶8节点杂交单元及减缩积分技术，消除数值分析过程中完全积分单元的“剪力自锁”现象.

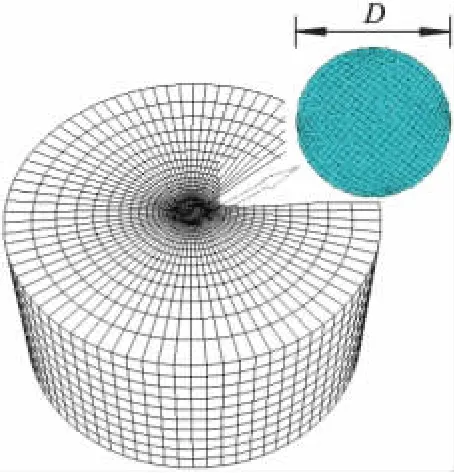
图2 有限元计算模型

在复合加载模式下，对应圆形基础底面中心处的竖向荷载、水平荷载、力矩荷载以及扭矩荷载，圆形基础将发生竖向位移、水平位移、转角位移，荷载分量和位移分量的符号规定与R.Butterfield等［10］的建议一致.

1.2 计算方法

在利用有限元进行数值计算的过程中，一般通过荷载控制方法或位移控制方法进行加载.与荷载控制方法相比，位移控制方法能够较准确地得到基础的荷载-位移曲线.当荷载-位移曲线的斜率接近于0或发生突变时，意味着荷载不变情况下基础的位移也会持续增大，因而可以确定此时地基达到了极限平衡状态，与极限平衡状态所对应的基础荷载就是地基的极限承载力，如图3所示.

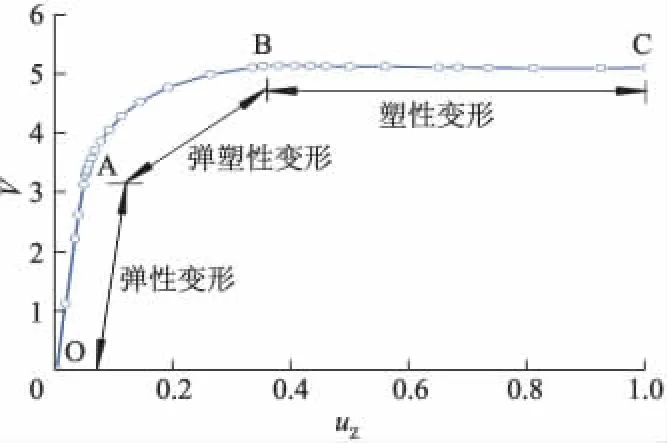
图3 荷载与位移关系图

为了较准确地求解复合加载模式下海床土体的极限承载能力，采用了swipe加载模式，利用位移控制方法搜寻地基的破坏包络面.swipe加载模式如图4所示，包括如下加载步骤:① 沿 i方向施加位移ui，直至i方向土体反力不再随位移增大而改变;②保持i方向的位移ui不变，而沿j方向施加位移uj，直到j方向所能提供的极限反力不随j方向位移增大而改变;③所形成的加载轨迹，可以近似地作为i向与j向荷载形成的破坏包络图.这种加载方式广泛应用于地基稳定性的数值模拟中.

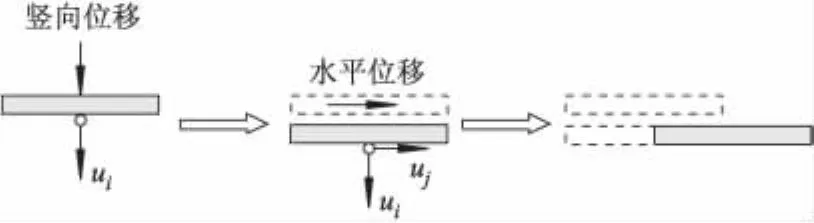
图4 Swipe加载模式

2 结果分析

2.1 V －Hx－My破坏包络面

复合加载模式下，为了系统研究不同竖向荷载V作用下H－M荷载空间中海床地基的极限承载能力，本研究分别在竖向荷载 V=0，0.2 Vult，0.4 Vult，0.6 Vult和0.8 Vult情况下，针对不排水饱和软黏土海床进行了大量数值计算，Vult表示单一竖向荷载作用下海床土体的极限承载能力.图5和图6分别为不排水饱和软黏土地基破坏包络曲线及其三维破坏包络面.其中M/ARSu和H/ASu分别为归一化力矩极限承载力和归化水平极限承载力.由图5，6可知:随着竖向荷载分量V的逐渐增大，H－M荷载空间中的地基破坏包络曲线的形状和大小均发生明显的改变;同二维条形基础破坏包络面曲线相比，当基底土体达到最大极限力矩承载能力时，三维圆形基础破坏包络面曲线更圆滑，包络面曲线不存在明显的斜率突变现象［11］.

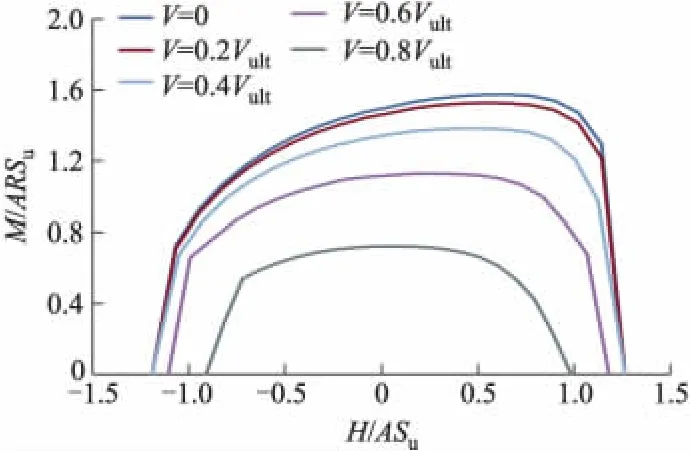
图5 破坏包络曲线

图5中，H和M分别为圆形基础形心处所受的水平荷载与力矩荷载;A和R分别为圆形基础底面积和圆半径;Su为海床土体不排水抗剪强度.当竖向荷载分量V较小时，破坏包络曲线关于M轴呈明显的非对称性，这种非对称性随着竖向荷载分量V的逐渐增大而逐渐减弱;当竖向荷载V≥0.8Vmax时，破坏包络曲线关于M轴基本对称.同时，计算结果表明:当竖向荷载V≤0.2Vmax时，海床土体破坏包络曲线的形状与大小变化不大;当竖向荷载V＞0.2Vmax时，破坏包络曲线的形状与大小变化非常明显.

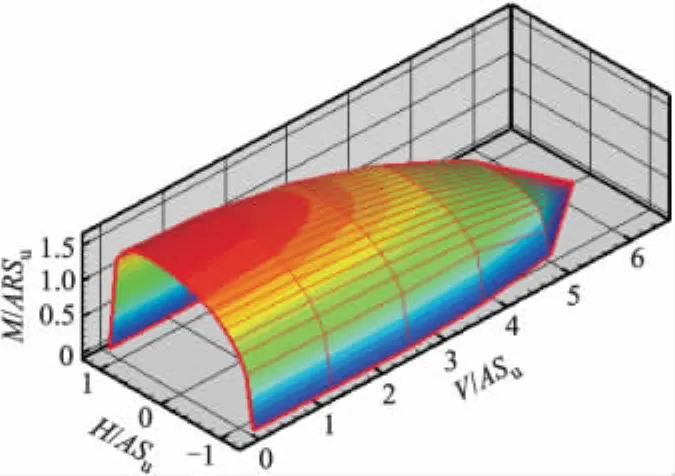
图6 三维破坏包络面

本研究中，V=0.6Vmax与 V=0.8Vmax两种情况对应的计算结果表明，竖向承载力后者比前者提高了33.3%，而最大力矩承载力M0降低了54.5%，水平承载力降低了21.8%，如表1所示.其中，Vult为海床土体竖向极限承载力，H0为竖向荷载作用下基础能够承受的最大水平荷载，M0为竖向荷载作用下基础能够承受的最大力矩荷载.

表1 竖向荷载、力矩荷载同水平荷载间变化关系

2.2 水平荷载对包络面影响

图7为水平荷载Hy作用下，当V=0.6Vult时，三维圆形基础V－Hx－My荷载空间地基土体破坏包络面曲线随Hy的变化规律.由包络面曲线可知，当Hy=0，0.3Hult，0.5Hult，0.7Hult时，包络面曲线呈现缩小趋势，表明水平荷载的出现，进一步降低了地基土体的极限承载能力.

图7 水平荷载对包络面影响

图8为三维圆形基础所能承受的最大水平荷载H0和力矩荷载M0随水平荷载Hy的变化规律.水平荷载Hy/Hult的变化，对基底土体的极限承载能力影响较为显著，即水平荷载加大了圆形基础V－Hx－My荷载空间中基底土体的失稳程度.本研究给出水平荷载对基底土体水平极限承载能力、力矩极限承载能力影响关系式，即

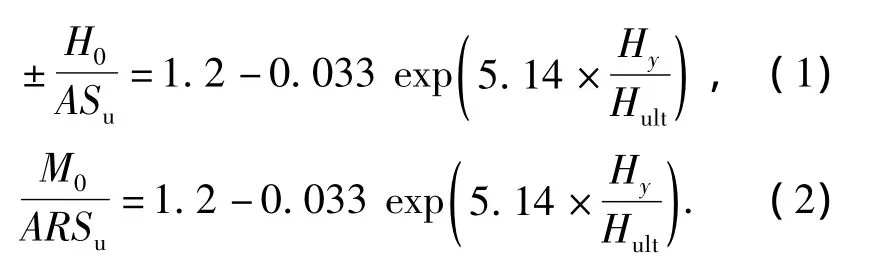
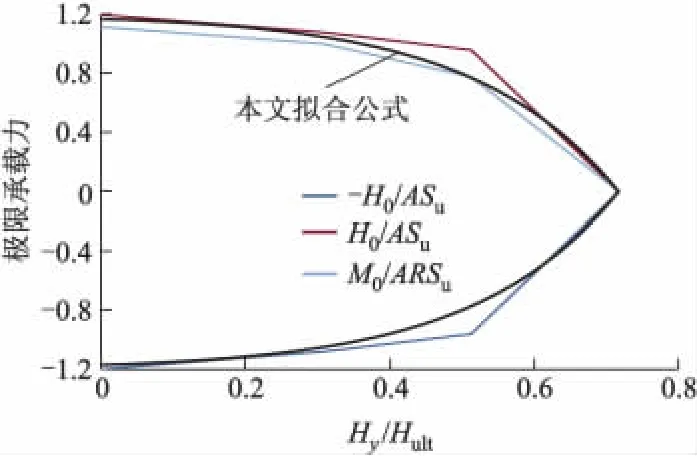
图8 极限承载力随水平荷载变化关系

2.3 力矩荷载对包络面影响

图9为力矩荷载Mx作用下，当V=0.6Vult时，三维圆形基础V－Hx－My荷载空间地基土体破坏包络面曲线随力矩荷载的变化规律.

由图9的包络面曲线可知，当Mx分别为0，0.3Mult，0.5Mult，0.7Mult时，包络面曲线呈现缩小趋势，表明力矩荷载的出现，进一步降低了地基土体的极限承载能力.

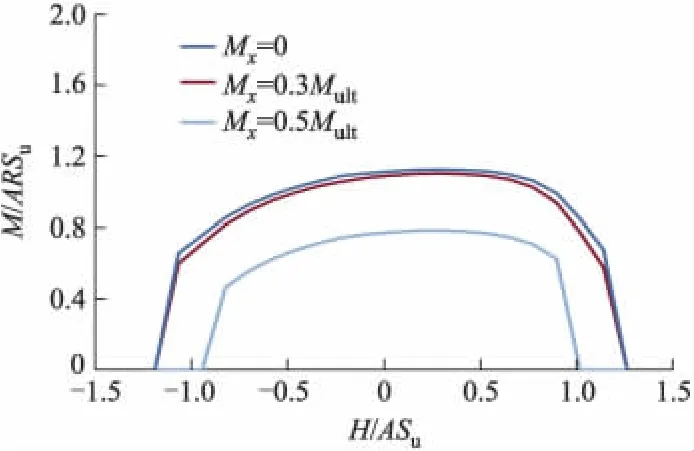
图9 力矩荷载对包络面影响

图10为三维圆形基础所能承受的最大水平荷载H0和力矩荷载M0随力矩荷载Mx的变化规律.当 Mx较小时(Mx≤0.3Mult)，Mx对基底土体的极限承载能力影响较弱，破坏包络面曲线变化不大，表明较小的Mx对圆形基础的稳定性影响较小;当Mx进一步增大时，基底土体的H0和M0变化十分明显，表明较大的Mx降低了圆形基础V－Hx－My荷载空间中基底土体的稳定性.

本研究给出力矩荷载对基底土体水平极限承载能力和力矩极限承载能力影响关系式，即

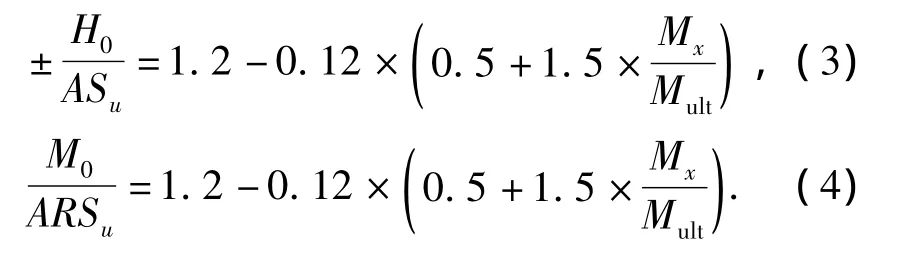
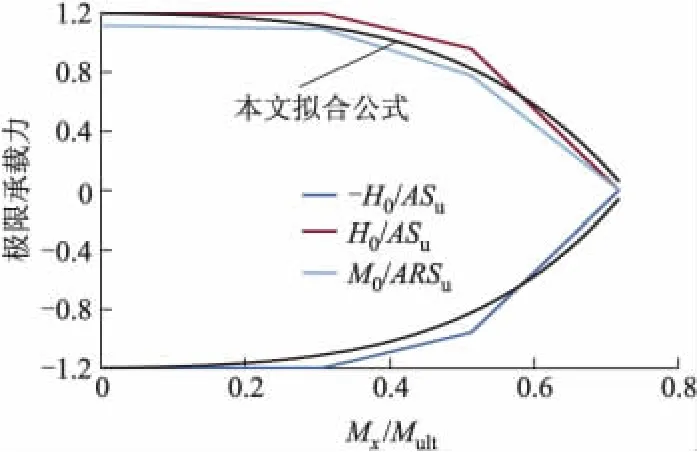
图10 极限承载力随力矩荷载变化关系

2.4 扭矩荷载对包络面影响

图11为扭矩荷载T作用情况下，当V=0.6Vult时，三维圆形基础V－Hx－My荷载空间地基土体破坏包络面曲线随扭矩荷载的变化规律.由包络面曲线可知，当 T=0，0.3Tult，0.5Tult，0.7Tult时，包络面曲线呈现缩小趋势，表明扭矩荷载T的出现，降低了地基土体的极限承载能力.

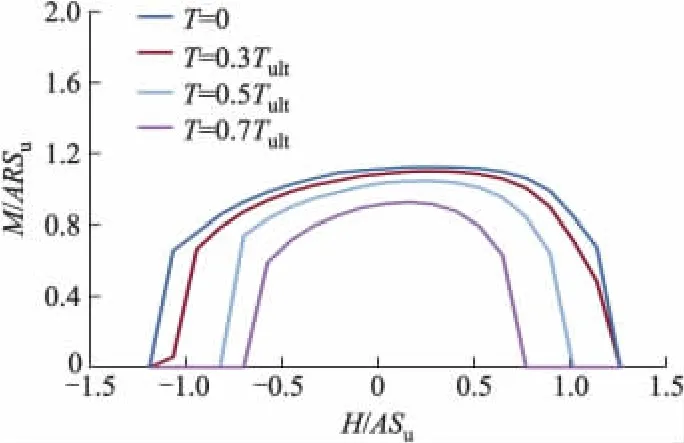
图11 扭矩荷载对包络面影响

图12为极限承载力随扭矩荷载变化关系曲线.其中T/Tult为扭矩荷载.由图12可知:当T较小时(T≤0.3Tult)，T对基底土体极限承载能力影响较弱，表明较小的T对圆形基础的稳定性影响较小;当T进一步增大时(T≥0.3Tult)，圆形基础基底土体最大水平极限承载力降低程度比极限力矩明显.

图12 极限承载力随扭矩荷载变化关系

3 结论

1)三维荷载空间中，圆形基础对应的破坏包络面曲线比二维条形基础对应的包络面曲线圆滑，包络面曲线不存在斜率突变段.

2)6自由度圆形基础破坏包络面曲线，受水平荷载和力矩荷载的影响较为明显，而扭矩荷载对包络面形状和大小影响较弱.

3)本研究给出的拟合公式(1)－(4)，对于深入研究6自由度破坏包络面方程具有参考价值.

References)

［1］Yuan Fanfan，Zhan Yungang，Luan Maotian.Bearing behavior of strip foundations on undrained two-layered subsoil subjected to eccentrical loading［C］∥Luan Maotian.Recent Development of Geotechnical and Geoenvironmental Engineering in Asia.Dalian:Dalian University of Technology Press，2006:241 －244.

［2］Zhang Q Y.Failure mode of foundation under combined loading［J］.EJGE，2008(13):1 －10.

［3］Taiebat H A，Carter J P.Bearing capacity of strip and circular foundations on undrained clay subjected to eccentric loads［J］.Geotechnique，2002，52(1):61 － 64.

［4］Merifield R S，Nguyen V Q.Two-and three-dimensional bearing-capacity solutions for footings on two-layered clays［J］.Journal of Geomechanics and Geoengineering，2006，1(2):151－162.

［5］Bransby M F，Randolph M F.Combined loading of skirted foundations［J］.Geotechnique，1998，48(5):637 －655.

［6］Ukritchon B，Whittle A J，Sloan S W.Undrained limit analysis for combined loading of strip footings on clay［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，1999，124(3):265－276.

［7］Salencon J，Pecker A.Ultimate bearing capacity of shallow foundations under inclined and eccentric loads，part I:purely cohesive soils［J］.European Journal of Mechanics and Applied Solids，1995，14:349 －375.

［8］Gourvenec S，Randolph M.Effect of strength non-homogeneity on the shape of failure envelopes combined loading of strip and circular foundations on clay［J］.Geotechnique，2003，53(6):575 －586.

［9］Zhang Qiyi，Luan Maotian，Wang Zhongtao.Study on failure mechanism and bearing capacity of three-dimensional rectangular footing subjected to combined loading［J］.China Ocean Engineering，2008，22(2):313 －330.

［10］Butterfield R，Houlsby G T，Gottardi G.Standardized sign conventions and notation for generally loaded foundations［J］.Geotechnique，1997，47(5):1051 －1054.

［11］张其一.复合加载模式下地基失效机制研究［J］.岩土力学，2009，30(10):2940－2944.Zhang Qiyi.Study of failure patterns of foundation under combined loading［J］.Rock and Soil Mechanics，2009，30(10):2940 －2944.(in Chinese)