基于双重傅立叶变换的永磁转子涡流损耗分析

张 涛，朱熀秋，孙晓东，杨泽斌

(1.江苏大学电气信息工程学院，江苏 镇江 212013;2.淮阴工学院电子与电气工程学院，江苏 淮安 223003)

高速永磁同步电机具有体积小、重量轻、高功率密度、高效率等独特优点，是特种电气传动系统的关键设备，在航空航天、飞轮储能、分布式发电等高速直驱领域具有广阔的应用前景［1－3］.永磁同步电机转子与定子磁场同步旋转，转子中产生的涡流损耗远小于定子铜耗和铁耗，常忽略不计.而高速永磁转子需采用护套保护永磁体，转子散热条件差，由齿槽效应引起的气隙磁场高次谐波在转子永磁体、转子轭和绑扎永磁体的护套中产生涡流损耗，可能会引起很高的温升，导致永磁体局部不可逆热退磁.特别是烧结钕铁硼永磁材料具有较大的电导率和较低的居里温度，热稳定性差，在高速、超高速永磁同步电机中尤为严重［4－5］.所以很有必要对高速永磁同步电机气隙磁场进行优化，以减小转子涡流损耗.转子涡流损耗主要是由定子磁动势的空间谐波、定子电流的时间谐波以及定子齿槽效应引起的的气隙磁场时空谐波产生［6－9］.其中定子电流时间谐波引起的损耗主要取决于控制策略［10］，定子磁动势的空间谐波引起的损耗和气隙磁场时空谐波引起的损耗主要取决于电机的定、转子结构.文献［11］采用有限元法分析了分数槽三相永磁电机定子绕组采用单层和双层绕组结构时的转子损耗;文献［12］研究了槽开口大小以及气隙长度对转子涡流损耗的影响，提出在永磁体外增加一薄层非导磁金属屏蔽环来减小转子铁心、永磁体和护套损耗，分析了屏蔽环的电导率和厚度对转子涡流损耗的影响;文献［13］研究了永磁电机转子护套采用不同材料时的转子损耗和对转子温升的影响.但永磁体磁化模式对转子涡流损耗影响的研究还未见报道.

文中拟在建立永磁同步电机转子涡流损耗数学模型基础上，基于二维静态有限元分析，提取气隙磁场样本数据;采用双重傅里叶变换，研究转子永磁体在平行磁化和Halbach磁化时，由齿槽效应引起的气隙磁场时空谐波和相应的转子涡流损耗;并采用瞬态时步有限元法，计算在空载状态下的转子涡流损耗.

1 高速永磁同步电机结构与损耗模型

面贴式高速永磁同步电机转子旋转时产生的离心力会使永磁体脱落，必须采用护套保护永磁体，护套与永磁体之间采用过盈配合，保证在最高转速时，永磁体与转子铁心之间存在正向压强，同时护套内表面应力不超过护套材料的应力极限.护套材料主要有碳纤维和高强度合金材料，采用碳纤维材料绑扎转子时，虽然工艺复杂，但是护套中无高频涡流损耗，同时护套厚度较薄，电机气隙厚度小，提高了电机的电磁性能，但由于碳纤维材料为热的不良导体，转子散热条件差.由齿槽效应引起的转子涡流损耗主要由气隙磁场高次谐波产生，在永磁同步电机中气隙磁场由永磁体磁场产生，永磁体磁化方式对气隙磁场高次谐波具有重要影响.磁化模式主要有平行磁化和Halbach磁化等，图1给出4极24槽面贴式永磁电机结构和永磁体2种磁化方式，为了减小永磁体涡流损耗，永磁环由小块永磁体组成.

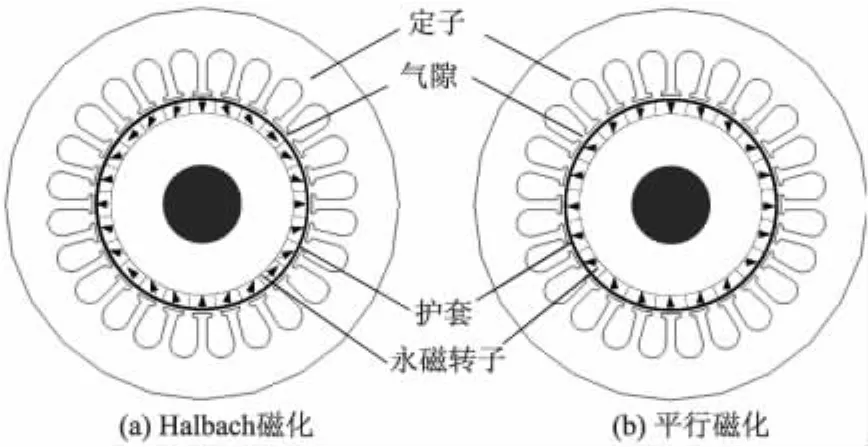
图1 四极高速永磁同步电机结构

为了建立永磁同步电机转子涡流损耗数学模型，图2给出了永磁同步电机二维直线模型.

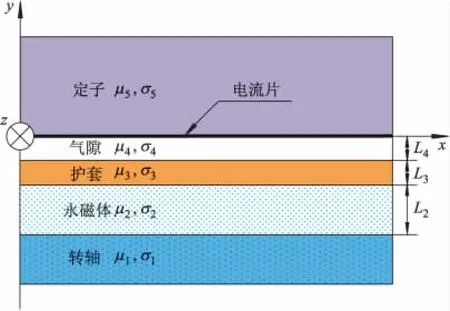
图2 永磁同步电机二维直线模型

由图2可见，模型分为5层，分别为定子铁心、气隙、永磁体、转子铁心和转轴，μi，σi(i=1，2，3，4，5)分别为每层材料的相对磁导率和电阻率.根据库伦规范

得到磁场基本控制方程为

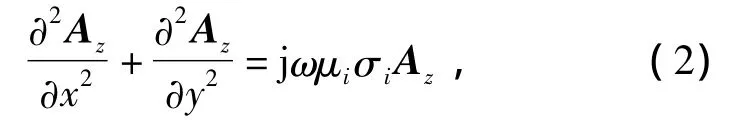
式中:Az为z轴矢量磁位.

根据经典麦克斯韦电磁场理论，在每层材料中有如下关系:

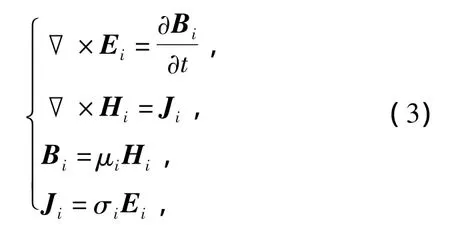
式中:Ei，Ji，Hi，Bi分别为第 i层材料的电场强度、涡流密度、磁场强度和磁感应强度.

忽略端部效应，根据斯托克斯定理，对电场强度Ei在路径C上进行积分，即有

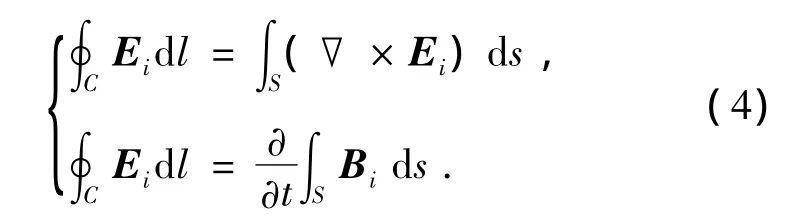
根据电磁功率计算公式，在体积V内的电磁损耗功率为

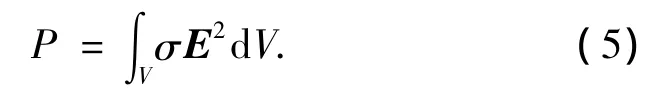
可得出在第i层材料中涡流损耗平均值为

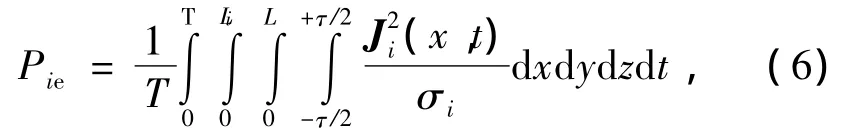
式中:τ为空间谐波极距;Li为每层材料厚度;L为轴向长度.

由于磁场的集肤效应，气隙磁场高次时空谐波的透入深度远小于护套厚度，所以转子涡流损耗主要在护套中产生.在转子笛卡尔坐标系下，建立气隙磁场磁通密度方程为

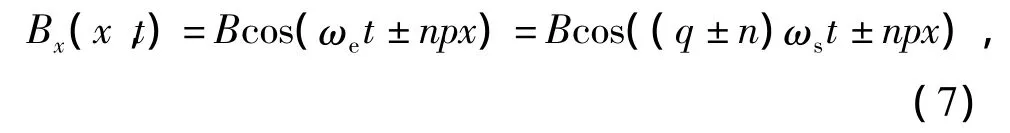
式中:q为时间谐波次数;n为空间谐波次数.转子表面的面电流密度和磁通密度关系为

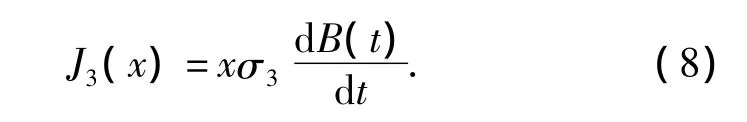
则将式(7)带入式(5)，可得

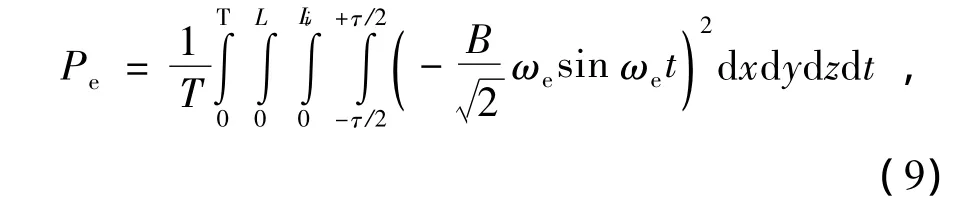
式中:ωe为谐波在转子中产生涡流的角频率.对上式进行积分可得

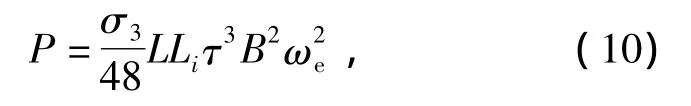
式中:τ为空间谐波极距.对于同一护套材料，谐波透入深度为

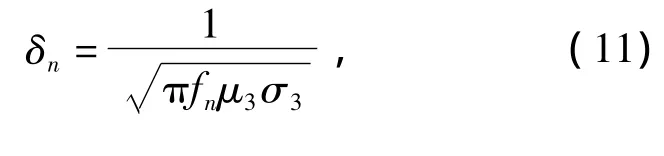
式中:fn为谐波频率.考虑谐波透入深度影响，转子损耗可表示为

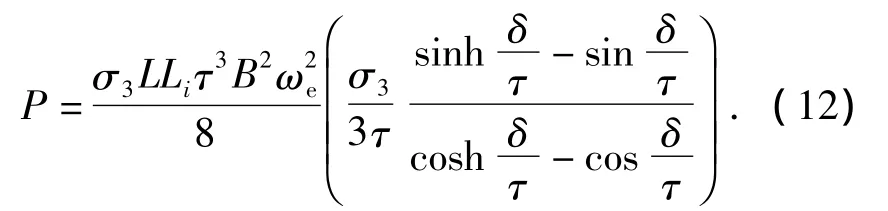
不同频率的高次谐波在转子中产生的总涡流损耗为

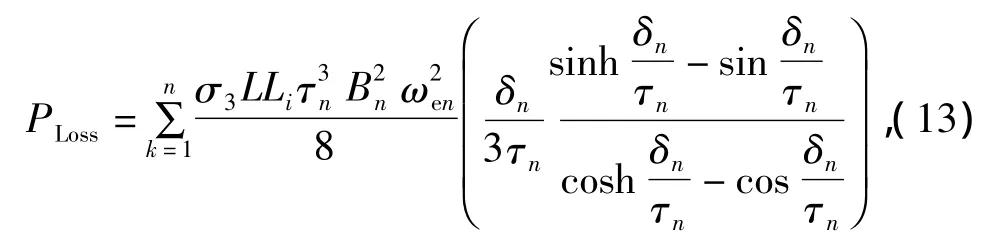
式中:n=6k±1;k=1，2，3，…;Bn为 n 次谐波磁通密度幅值;ωen，τn，δn分别为 n 次谐波产生涡流的角频率，极距和透入深度.

2 气隙磁场谐波分析

试验样机参数如下:定子槽数，24;极对数，2;定子内半径，33.5 mm;外半径，60 mm;气隙和护套厚度，2 mm;永磁体厚度，2 mm;转子铁心内径，29.5 mm;永磁体采用具有高磁能积的烧结钕铁硼材料，剩余磁感应强度为 1.22 T;矫顽力为900 kA·m－1.采用Maxwell-2D建立有限元分析模型，根据区域面积设定网格剖分密度，网格剖分结果如图3a所示，转子在0°时的永磁磁场静态磁通密度矢量分布如图3b所示，定子轭中的磁通密度约为1 T，磁极处的磁通密度最大，约为1.5 T，转子轭中的磁通密度约为0.55 T.

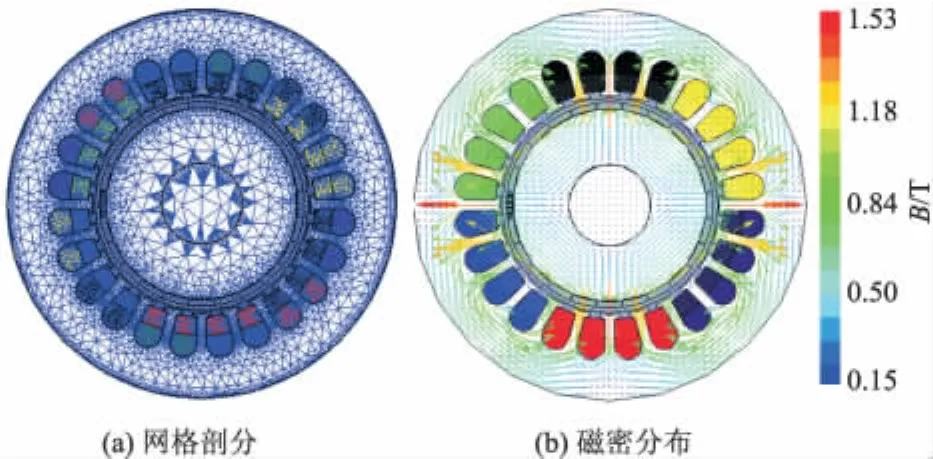
图3 网格剖分与磁场分布

转子在0°位置时，分别提取2种磁化模式下的气隙中心处磁通密度数据，并分析各次谐波，磁场波形和谐波分解结果如图4所示.

由图4可见，永磁体采用Halbach磁化时，气隙磁场波形近似为正弦波;而永磁体采用平行磁化时，气隙磁场波形近似为矩形波.采用傅里叶变换对气隙磁场数据进行谐波分解，从分析结果可得，气隙磁场由基波和频率为基波的奇数倍高次谐波组成，永磁体采张涛用Halbach磁化时，可以大大削弱第3，7，9，11 次等高次谐波.

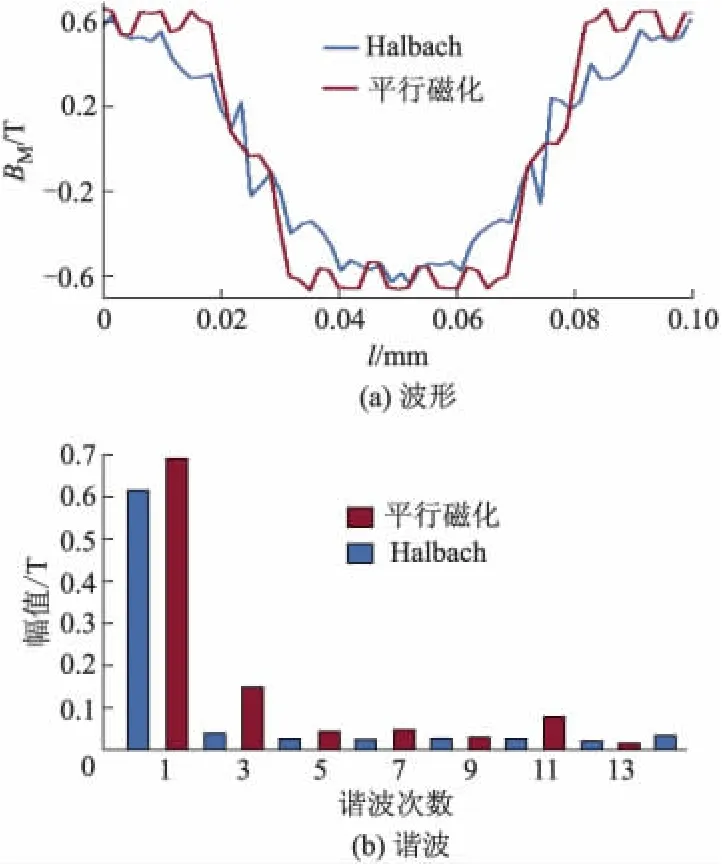
图4 气隙磁场波形与谐波分析

为了对2种磁化模式下的磁场谐波和涡流损耗进行定性分析，基于磁场静态分析，转子每旋转1°，提取一次转子表面气隙磁密法向分量数据，共提取30组数据进行分析.为获得时空谐波幅值，对所采集的数据样本采用离散傅里叶算法进行双重傅里叶变换.

傅里叶变换公式为

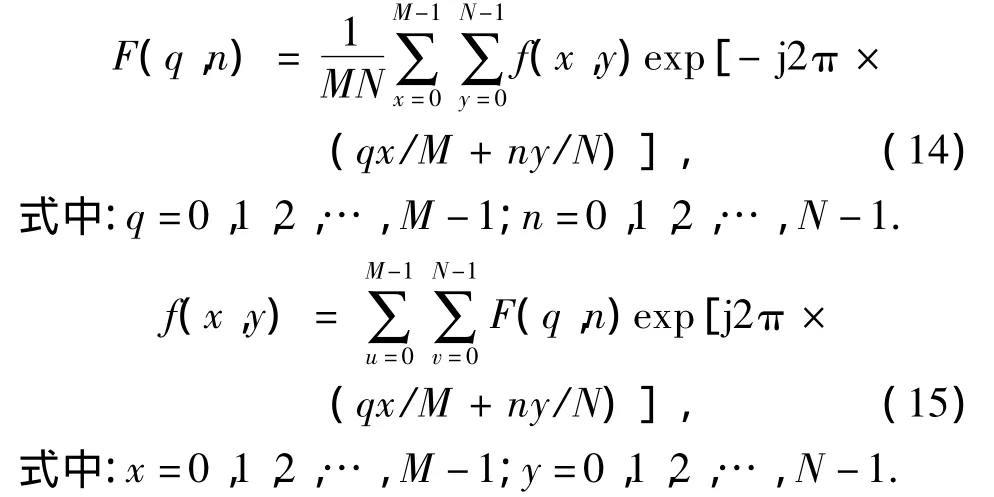
离散函数f(x，y)为在不同的时间x和角位置y时的磁通密度法向分量采样数据.函数F(q，n)为时间次数为q和空间次数为n的时空谐波.对连续函数的采样增量Δx和Δy的计算式为

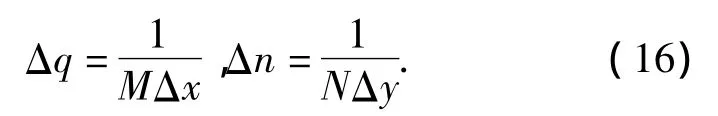
2种磁化模式下的转子表面气隙磁场时空谐波双重傅里叶分析结果二维矩阵如表1，2所示.

由表1，2可见，幅值较大的时空谐波F(q，n)为时间次数为12次和24次，空间次数为第11次、13次和第23次、25次的谐波.与平行磁化相比，永磁体采用Halbach磁化模式时，无 n=5，7，9次的谐波，同时 n=11，13，23，25 次的谐波幅值较小，有效降低了各时空谐波幅值.

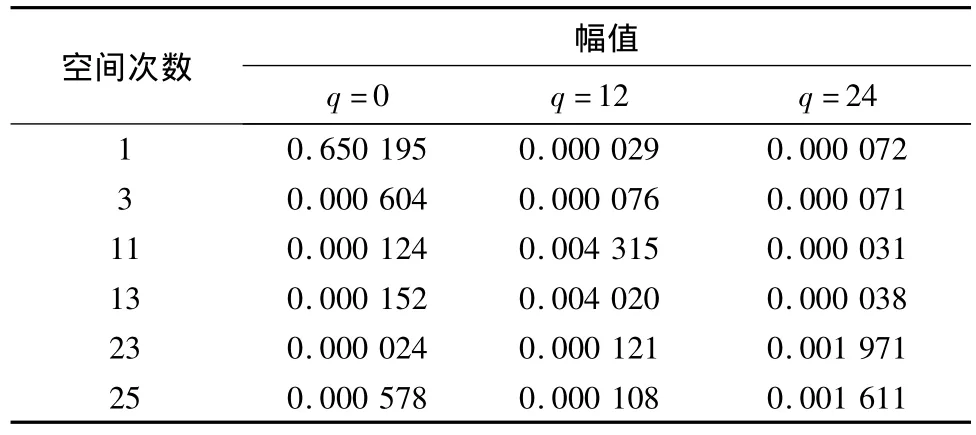
表1 Halbach磁化谐波

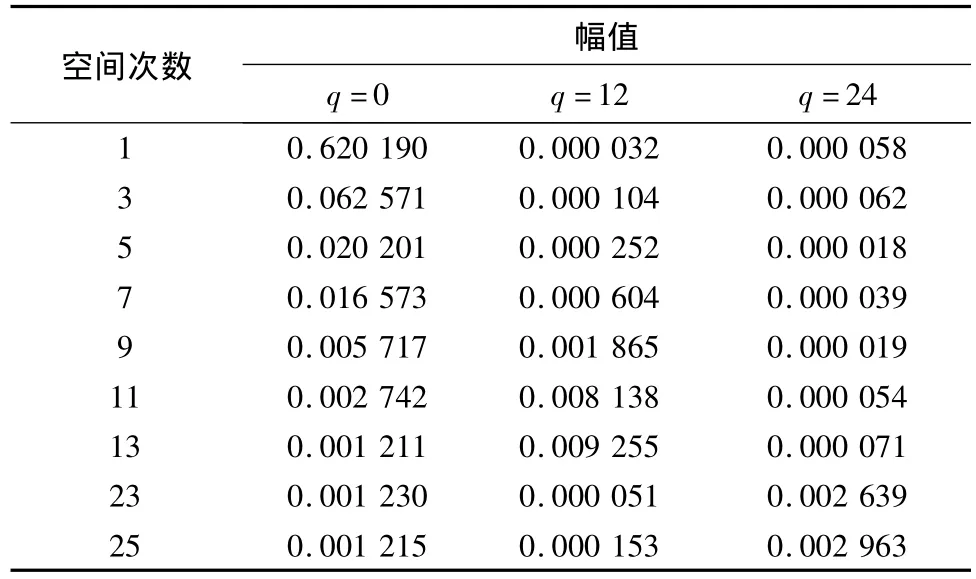
表2 平行磁化谐波

3 转子损耗计算

对各次时空谐波分别计算相应的涡流损耗密度，结果如表3，4所示.

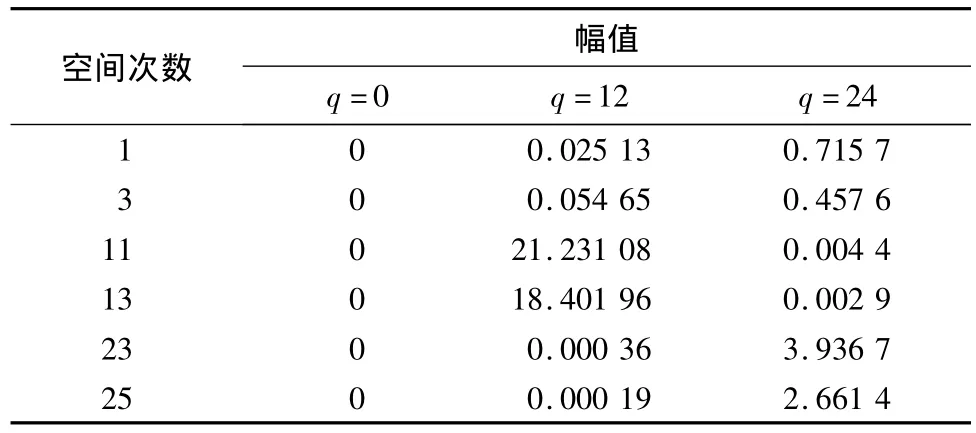
表3 Halbach磁化转子损耗密度

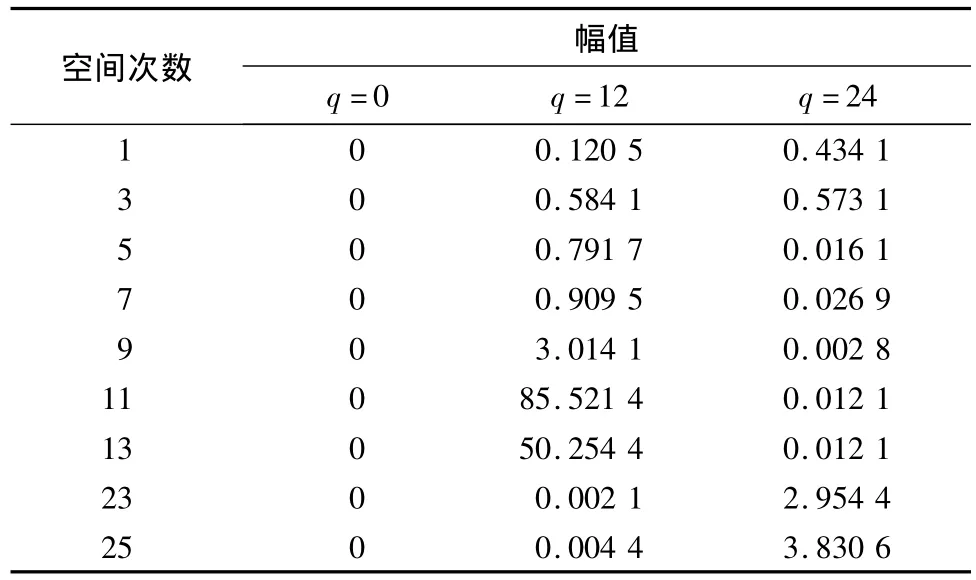
表4 平行磁化转子损耗密度

由表3，4可见，永磁体在Halbach磁化和平行磁化时，各时空谐波产生的转子损耗密度主要由时间次数q=12，空间次数n=11，13;和q=24，空间次数n=23，25的谐波产生.

图5给出了由时空谐波引起的转子涡流损耗密度柱状比较图.

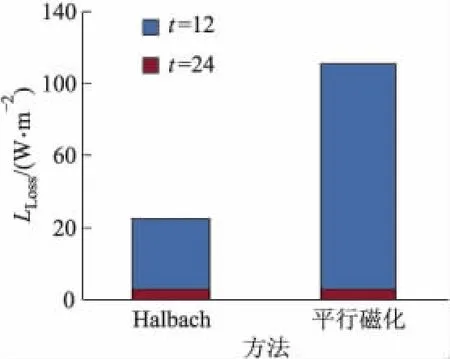
图5 转子损耗密度

由图5可见，永磁体采用Halbach磁化时的转子涡流损耗密度远小于平行磁化时的转子涡流损耗密度，约为平行磁化时的34%.

4 瞬态有限元分析

采用时步有限元法对已建立的有限元模型进行分析.在空载状态下，计算由齿槽效应引起的气隙磁场时空谐波在转子中产生的涡流损耗.转子旋转速度为48 kr·min－1，计算时间为 0 ～0.04 s，时间步长设定为0.002 s，对转子区域设定涡流损耗求解.图6给出在转子稳定旋转时的涡流损耗密度分布.

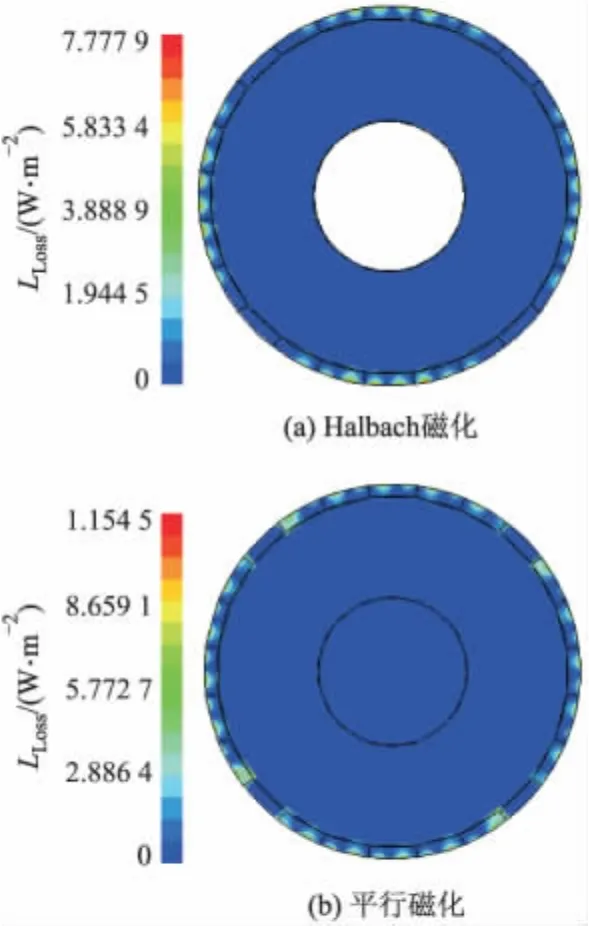
图6 转子损耗密度分布

由图6可见，由于磁场的集肤效应，转子涡流损耗主要集中于转子表面的护套和永磁体中;对于相同尺寸的永磁转子，永磁体采用Halbach磁化模式时，由于含有较少的气隙磁场谐波分量转子其涡流损耗密度为44 W·m－2;而采用平行磁化时损耗密度为130 W·m－2.高速永磁同步电机转子永磁体采用Halbach磁化模式时的转子涡流损耗约为平行磁化时的34%.永磁体采用Halbach磁化模式能够有效减小由气隙磁场齿槽效应引起的转子涡流损耗，与理论计算结果一致.

5 结论

文中采用双重傅里叶变换和2-D有限元法，对齿槽效应引起的气隙磁场时空谐波在转子中产生的涡流损耗进行研究;比较了永磁体两种磁化模式下的气隙磁场时空谐波与对应的涡流损耗;涡流损耗主要由空间次数为13、15和23、25，时间次数为12和24的时空谐波产生;永磁体采用Halbach磁化模式的转子涡流损耗为平行磁化模式时的34%.

References)

［1］张 涛，朱熀秋，孙晓东，等.基于有限元法的高速永磁转子强度分析［J］.电机与控制学报，2012，16(6):63－68.Zhang Tao， Zhu Huangqiu， Sun Xiaodong， et al.Strength analysis on high-speed permanent magnet rotor using finite element method［J］.Electric Machines and Control，2012，16(6):63 －68.(in Chinese)

［2］Bianchi N，Bolognani S，Luise F.Potentials and limits of high-speed PM motors［J］.IEEE Transactions on Industry Applications，2004，40(6):1570 －1578.

［3］徐永向，胡建辉，胡任之，等.永磁同步电机转子涡流损耗计算的实验验证方法［J］.电工技术学报，2007，22(7):150－154.Xu Yongxiang，Hu Jianhui，Hu Renzhi，et al.An experimental verification method of calculation for rotor eddy current losses in PMSMs［J］.Transactions of China Electrotechnical Society，2007，22(7):150 －154.(in Chinese)

［4］徐永向，胡建辉，邹继斌.表贴式永磁同步电机转子涡流损耗解析计算［J］.电机与控制学报，2009，13(1):63－66.Xu Yongxiang，Hu Jianhui，Zou Jibin.Analytical calculation of rotor eddy current losses of surface-mounted PMSM［J］.Electric Machines and Control，2009，13(1):63 －66.(in Chinese)

［5］Zhang Yuqiu，Lu Kaiyuan，Ye Yunyue.Permanent magnet eddy current loss analysis of a novel motor integrated permanent magnet gear［J］.IEEE Transactions on Magnetics，2012，48(11):3005 －3008.

［6］周凤争，沈建新，林瑞光.从电机设计的角度减少高速永磁电机转子损耗［J］.浙江大学学报:工学版，2007，41(9):1587－1591.Zhou Fengzheng，Shen Jianxin，Lin Ruiguang.Reduction of rotor loss in high-speed permanent magnet motors by design method［J］.Journal of Zhejiang University:Engineering Science，2007，41(9):1587 － 1591.(in Chinese)

［7］Yamazaki Katsumi，Kanou Yuji，Fukushima Yu，et al.Reduction of magnet eddy-current loss in interior permanent-magnet motors with concentrated windings［J］.IEEE Transactions on Industry Applications，2010，46(6):2434－2441.

［8］Yamazaki Katsumi，Abe Atsushi.Loss investigation of interior permanent-magnet motors considering carrier harmonics and magnet eddy currents［J］.IEEE Transactions on Industry Applications，2009，45(2):659 －665.

［9］Yamazaki Katsumi，Fukushima Yu，Sato Makoto.Loss analysis of permanent-magnet motors with concentrated windings-variation of magnet eddy-current loss due to stator and rotor shapes［J］.IEEE Transactions on Industry Applications，2009，45(4):1334 －1442.

［10］Okitsu T，Matsuhashi D，Muramatsu K.Method for evaluating the eddy current loss of a permanent magnet in a PM motor driven by an inverter power supply using coupled 2-D and 3-D finite element analyses［J］.IEEE Transactions on Magnetics，2009，45(10):4574 －4577.

［11］Bianchi N，Bolognani S，Fornasiero E.An overview of rotor losses determination in three-phase fractional-slot PM machines［J］.IEEE Transactions on Industry Applications，2010，46(6):2338 －2345.

［12］田占元，祝长生，王 玎.飞轮储能用高速永磁电机转子的涡流损耗［J］.浙江大学学报:工学版，2011，45(3):451－457.Tian Zhanyuan，Zhu Changsheng，Wang Ding.Rotor eddy current loss in high speed permanent magnet motors for flywheel energy storage system［J］.Journal of Zhejiang University:Engineering Science，2011，45(3):451 －457.(in Chinese)

［13］Kolondzovski Z，Belahcen A，Arkkio A.Comparative thermal analysis of different rotor types for a high-speed permanent-magnet electrical machine［J］.IET Electric Power Applications，2009，3(4):279 －288.