混合遗传算法在网络拥塞控制中的仿真研究
2013-08-22路银川孔金生
赵 静,路银川,孔金生
(1. 中州大学 工程技术学院,郑州 450044;2. 郑州大学 电气工程学院,郑州 450002)
0 引言
过多的报文存在于网络时,会引起网络性能下降,即发生了拥塞[1]。拥塞的出现会增加链路的丢包率、加大节点之间的延迟、加剧网络抖动、降低网络吞吐量。拥塞的发生虽然意味着网络能够提供给用户的资源远远小于用户的需求量,但是单一的增加网络资源不能缓解该现象,反而会加重拥塞程度。因此,采用有效的方法实现拥塞控制已成为当前网络研究的热点问题。
目前,人们提出了很多算法,如RED、REM[2]、Drop Tail队列管理、DRED[3]、PI控制器[4]、PID控制器[5]等。但是它们都存在一些缺陷,如RED和Drop Tail算法受主观因素影响大,稳定性差,鲁棒性不强,控制过程中容易产生错误的数据,甚至发生丢失;PI控制器、REM、DRED、PID控制器等算法的动态性能不好,队列波动较大。由于智能仿生类优化算法具有并行性和自适应能力好、鲁棒性强等优点,特别适用于网络拥塞控制[6,7]。但以往的研究大多是在网络的带宽、延迟等服务质量(QoS)参数一定的情况下,利用智能优化算法选择一条满足多个QoS要求的最佳路径,这些研究方法其实更偏向于网络调度。
为了实现避免网络拥塞、改善网络性能,本文在已有优化算法的基础上,将遗传算法和禁忌搜索算法结合起来,提出了一种混合遗传算法,仿真结果表明这种算法能可靠、有效地实现拥塞控制。
1 QoS路由优化数学模型
计算机网络规模庞大、结构复杂,为了能够分析各种网络拥塞控制策略,同时满足用户的网络服务质量要求,需要建立QoS路由优化数学模型,其优化原则为:在保证带宽和延迟等QoS参数满足要求的前提下,尽可能减少使用的网络资源,并均匀分布各处的网络负载。这属于NP-hard问题,不能得到最优解,只能找寻次优解,因此本文构造的QoS路由优化数学模型的表达式为:
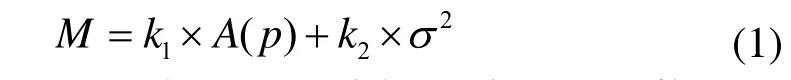
其中,A(p)称为资源消耗函数,反映的是网络中某一业务量在所选路径p中占用的网络资源量,可表示为:
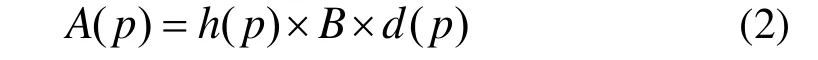
式中,h(p)为所选路径p的跳数;B为业务量的请求带宽;d(p)为路径p的延迟。显然,若路径的h(p)越少、d(p)越小,它占用的网络资源就少。
σ2为某条路径p上链路利用率的方差,反映的是负载在该路径上均衡分布的程度,可表示为:
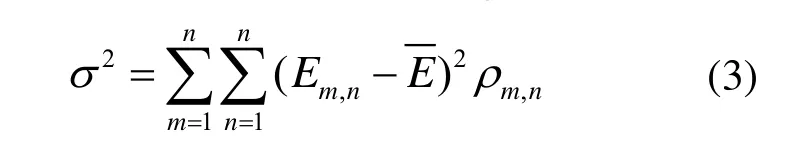
式中,Em,n为节点m到节点n的链路利用率;为Em,n的均值;若m→n的链路属于所选路径,则ρm,n为1,否则,ρm,n为0。
k1和k2是两个正实数,若取值适当可使目标函数M的两部分基本相等。
因此,网络拥塞控制问题可以描述为:在网络拓扑结构已知的情况下,采用优化算法对链路的带宽和延迟等参数进行优化,从而使目标函数M最小。
遗传算法(GA)的全局搜索能力强,但却具有较差的爬山能力、容易出现早熟;禁忌搜索(TS)的爬山能力强,但却需要通过经验去选择初始参数,鲁棒性差。为了弥补两种算法的缺点,提高优化效率,本文在GA中融入TS的思想,提出了一种混合遗传算法。
2 混合遗传算法的实现
该算法的程序设计流程图如图1所示。
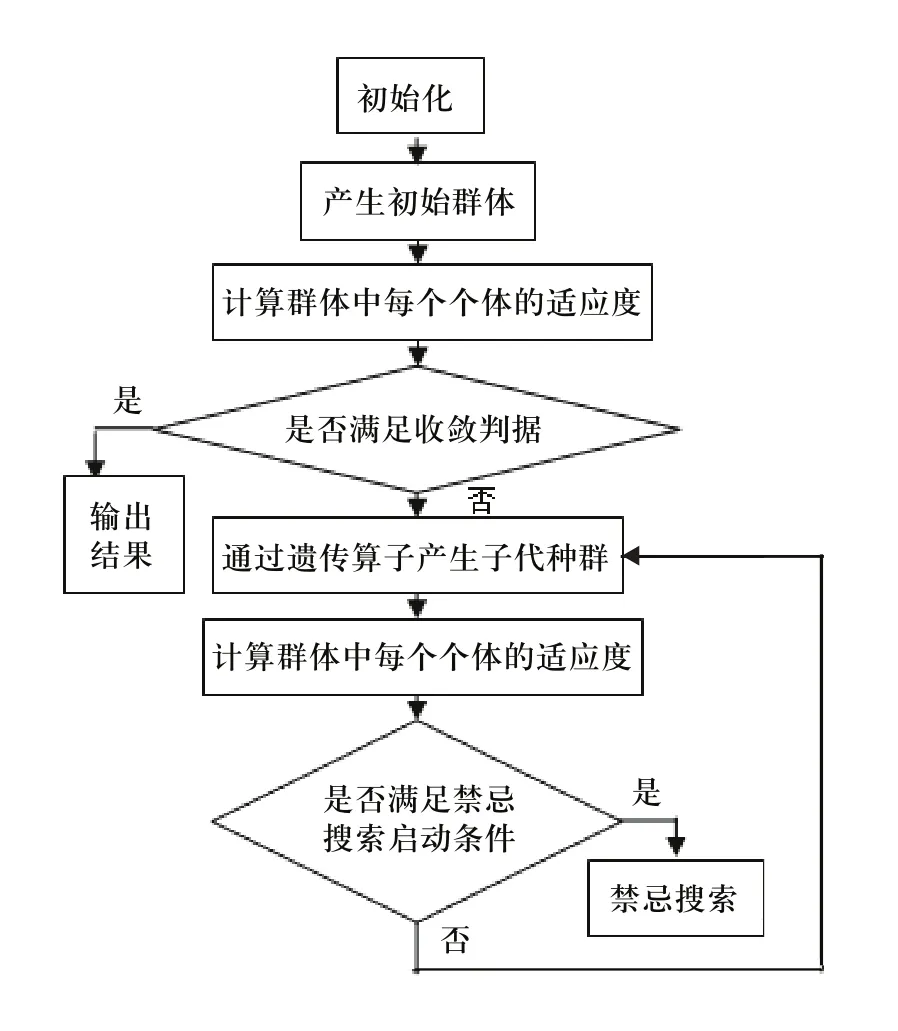
图1 混合遗传算法的程序设计流程图
2.1 编码
遗传算法常用到的编码方法有二进制编码、十进制编码、实数编码等。为了便于描述优化问题,提高算法的精度,本文采用实数编码。
2.2 适应度函数
适应度函数能反映同一群体中不同个体的优劣,是选择操作的依据,通常采用最大值的形式。由于优化数学模型(1)式为最小值问题,所以本文采用对其求倒数的办法来获取适应度函数,即:
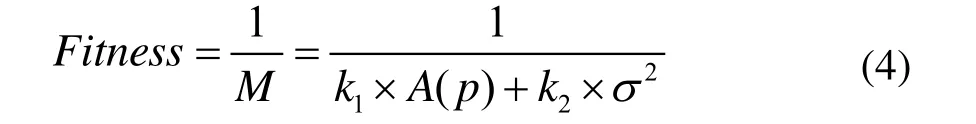
2.3 选择
采用最基本的轮盘赌选择。在这种方法中,个体进入下一代的概率Pi可表示为:
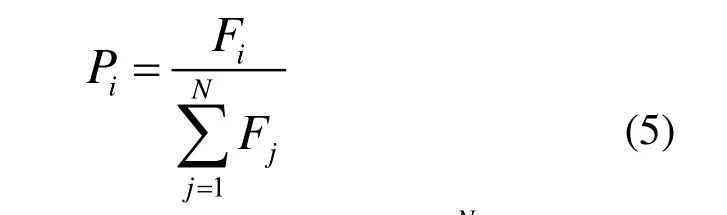
式中,Fi为该个体的适应度值;为种群中所有个体适应度值之和。
2.4 交叉和变异
采用自适应交叉、变异操作,交叉率Pc和变异率Pm的自适应调整公式为:
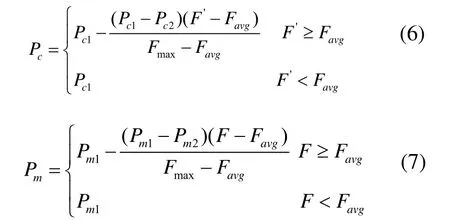
式中,Pc1、Pc2、Pm1和Pm2均为常数;Fmax为群体中最优个体的适应度;Favg为群体的平均适应度;F′为交叉操作中适应度值较大的个体;F 为要变异个体的适应度值。根据个体自身的性能好坏,选择合适的Pc和Pm。
2.5 移动
经过选择、交叉、变异操作,遗传算法为禁忌搜索产生了较好的初始个体。禁忌搜索按照特定的搜索方向“移动”,每次“移动”产生一个试验个体。根据编码特点,本文采用单点移动,即在码串中随机选择一位,按照设定好的步长递增或递减。
2.6 禁忌表
禁忌表对已经进行的优化过程进行记录和选择,可防止禁忌搜索陷入局部最优。这里采用动态设置方式,即每次循环结束,将最早进入禁忌表的反方向“移动”替换成当前的反方向“移动”,并定义“移动”的禁忌长度,最后将其它反方向“移动”的禁忌长度都减1。
2.7 特赦准则
为了尽可能不错过产生最优解的“移动”,禁忌搜索还采用了“特赦准则”策略,并保留最优个体记录,以便替代下一代中的最劣个体。
2.8 终止条件
该混合优化算法中存在两个循环:内循环和外循环。内循环的终止条件是禁忌搜索的最大允许迭代次数;外循环的终止条件有两个:遗传算法的最大允许迭代次数和优化判据,其中优化判据为禁忌搜索前后最优个体适应度值的变化是否不大于某个给定的常数。
3 仿真研究
3.1 网络参数设置
为了验证该混合遗传算法的有效性,对图2所示的网络拓扑图进行仿真研究。
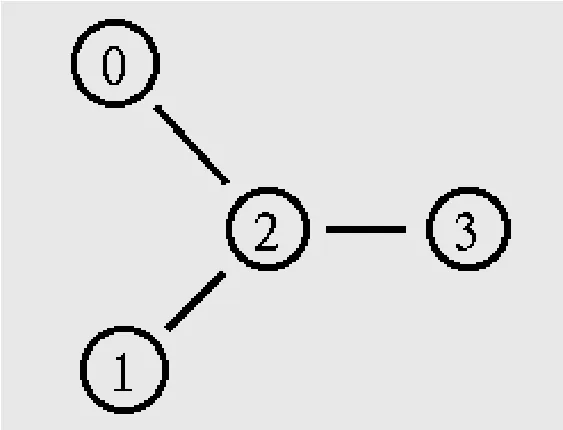
图2 网络拓扑图
网络中的每条链路设置一组QoS参数:[带宽延迟]=[1Mb 10ms]。假设源节点0和1上有两个相同的流量发生器cbr0和cbr1,每隔5ms便产生500Byte大小的数据分组,流向目的节点3。cbr0封包在0.5s时开始发送,4.5s时停止;cbr1封包在1.0s时开始发送,4.0s时停止。由于节点0和节点1的请求带宽为0.8Mb,而链路2-3的带宽仅为1Mb,当两组业务流共同流经链路2-3时,必定会出现争夺网络资源的现象,从而引起网络拥塞。下面利用本文提出的混合遗传算法对链路2-3的带宽和延迟参数进行优化。
3.2 结果分析
3.2.1 网络性能的比较
优化前后cbr0封包和cbr1封包的情况见表1。图3、图4分别为优化前后cbr0和cbr1封包端到端的延迟时间。从仿真结果可以看出,利用混合遗传优化算法对网络参数优化后,减小了封包端到端的延迟时间,避免了网络拥塞。
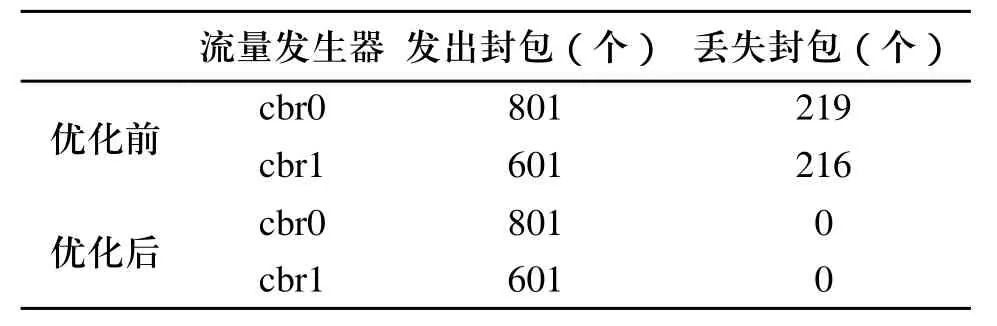
表1 优化前后封包情况
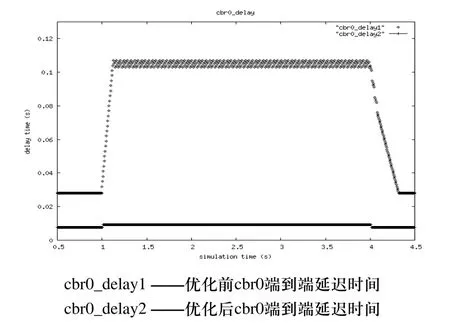
图3 cbr0封包端到端的延迟时间
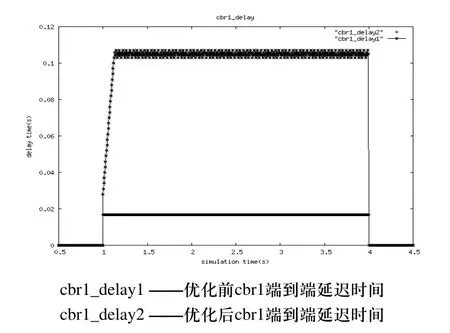
图4 cbr1封包端到端的延迟时间
3.2.2 QoS参数的平均优化结果
为了进一步验证本文中混合遗传算法的优化性能,采用GA对同一网络进行优化,对比两种算法的收敛特性,其结果如图5所示。由图5可知:混合遗传算法在第70代左右就生成了最优目标函数值,而GA在第80代左右才生成最优目标函数值;而且,经混合遗传算法优化后的目标函数值小于GA优化后的目标函数值。这说明混合遗传算法具有较快的收敛速度,全局优化性能好。

图5 平均收敛特性的对比
4 结束语
针对网络拥塞现象,本文提出了一种避免网络拥塞的混合遗传算法。该算法结合了遗传算法和禁忌搜索的特点,既避免了遗传算法陷入局部最优解,又为禁忌搜索提供了较好的初始个体,减少调用的次数,加快了算法的收敛。仿真结果反映出该混合遗传算法在减小网络资源利用、均衡分布负载的同时,可以降低丢包率、减小端到端的延迟时间,达到避免网络拥塞的目的,为进一步实施拥塞控制提供了有效途径。
[1] JACOBSON V. Congestion Avoidance and Control[J].ACM Computer Communication Review, 1988,18(4):314-329.
[2] ATHURALLYA S, LI V H, LOW SH, et al. REM: Active Queue Management[J]. IEEE Network, 2001, 15(3):48-53.
[3] AWEYA J, OUELLETTE M, MONTUNO D Y. A Control Theoretic Approach to Active Queue Management[J].Computer Networks, 2001, 36(2): 203-235.
[4] HOLLOT C V, MISRA V, TOWSLEY D. On Designing Improved Controllers for AQM Routers Supporting TCP Flows[C]. In Proceedings of IEEE INFOCOM,2001:1726-1734.
[5] 任丰原,王福豹,任勇,山秀明.主动队列管理中的PID控制器[J]. 电子与信息学报, 2003, 25(1): 94-99.
[6] 金琼,周世纪,彭燕妮.基于改进遗传算法的QoS路由选择优化[J]. 计算机应用, 2005, 25(2):256-258.
[7] 陈曦.基于免疫粒子群优化算法的多约束路由选择算法[J]. 长沙交通学院学报,2006,22(2):56-59.
