基于改进EMD 的结构模态参数识别比较研究

付春 朱磊 牟海东

(1.辽宁石油化工大学石油天然气工程学院，辽宁抚顺 113001; 2.北京泰克华诚技术信息咨询有限公司，北京 100083)

1998年，N.E.Huang等人创造性地提出了适用于分析非线性非平稳信号的HHT(Hilbert Huang Transform)方法，该方法作为一种新的时频分析法具有良好的自适应性［1，2］。该方法主要由经验模态分解(Empirical Mode Decomposition，EMD)和 Hilbert变换两部分组成，其核心是EMD过程。

然而在实际应用中，EMD方法存在诸如模态混叠现象等缺陷，这大大限制了它在实际中的应用。近些年来学者们不断提出一些改进的方法［3-6］。Huang本人也提出了利用中断检测来解决EMD分解过程中的模态混叠现象，其基本思想是对分解结果进行直接观察，如果存在模态混叠，则重新进行分解。这种改进方法在一定程度上可以避免模态混叠现象的发生，然而该方法具有分解效率低，需要人为后验判断等缺陷。

除了Huang本人，其他学者也提出了一些改进方法［3-6］，其中主流方法是基于多分辨率的改进EMD方法，其基本思路是通过频带滤波来界定每一个本征模函数(Intrinsic Mode Function，IMF)的尺度范围从而解决模态混叠的现象。2009年，Huang本人的研究小组根据大量的基于对EMD分解白噪声结果统计特性的研究提出了 EEMD(Ensemble Empirical Mode Decomposition，EEMD)方法，其本质是对待分析信号加噪声进行辅助分析的EMD改进方法，即利用高斯白噪声频率均匀分布的这种统计特性，从而使信号在加入高斯白噪声后在不同尺度上具有连续性，从而解决经典EMD中的模式混叠问题。

本文针对这两种主流改进方法进行了比较分析，并通过实验室一个7层框架的实验来比较和验证两种改进方法的优劣。

1 改进EMD(Improved EMD，IEMD)

为了解决经典EMD模态混叠的问题，提出了利用频带滤波对经典EMD做预处理，然后利用相关系数来判定真正的IMFs，其原理可以表述为:

1)首先利用快速傅里叶变换对待分析信号进行频谱分析，初步估计出每个固有频率的大致范围。

2)使待分析信号分别通过1)确定的指定频率范围的带通滤波器，即将原信号分解为有限个窄带信号之和。

3)对通过滤波器得到的j个窄带信号分别应用EMD进行分解，去除其他频率成分的影响，此处j=1，2，3，…，n。

4)计算每个频带获得的本征模函数和原信号的相关系数，来判定真正的本征模函数。这里，首先将得到的所有本征模函数和原信号进行归一化处理，然后计算所有本征模函数与原信号的相关系数μi，并与相关系数的初始值ρ相比较，如果μi≥ρ，则可以判定为真正的本征模函数，否则被剔除，真正本征模函数的判定标准可以用下式来表达:

其中，η为一个比1.0更大的因子，通常取1～20，本文取η=10。

2 总体平均经验模态分解

为了解决经典EMD分解过程中存在模态混叠的缺陷，2009年，Huang等人继经典EMD之后提出了总体经验模式分解(Ensemble Empirical Mode Decomposition，EEMD)方法［7］。

EEMD方法其本质上是一种噪声辅助信号处理方法。其基本原理可以简单的表述为:利用白噪声频谱的均匀性和零均值的特性，将待分析信号中加入白噪声，那么当信号加在遍布整个时频空间分布一致的白噪声背景上时，再进行经典EMD过程时，就可以将不同时间尺度的信号自动分布到合适的参考尺度上。由于白噪声具有零均值的特性，那么，利用多次求平均的方法可以将噪声相互抵消去除，因此，集成均值的结果就可以作为最终结果。

EEMD的分解步骤可以简单的描述为:

1)将待分析信号中加入正态分布白噪声，生成新的分析信号。

2)将混有白噪声的新信号分解成有限个IMF分量。

3)重复步骤1)，步骤2)，每次向原信号中加入不同的白噪声序列(幅值相同)。

4)将每次得到的IMF集成并取其均值作为最终的IMF。

3 Hilbert变换

图1 实验室钢框架模型

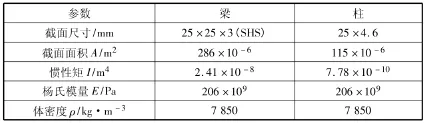
表1 结构构件特性

假设x(t)为测量信号，其Hilbert变换为:

图2 实测加速度响应

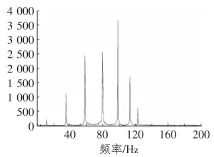
图3 FFT频谱图

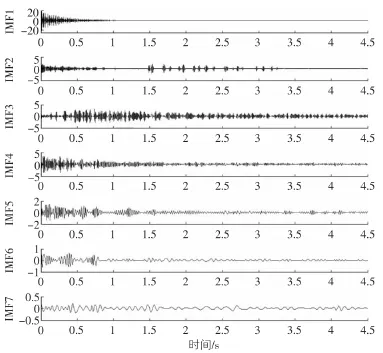
图4 经典EMD分解得到的部分IMFs

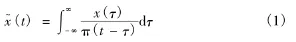
其中，A(t)为瞬态幅值;θ(t)为瞬态相位角;i=(－1)1/2。信号的瞬态频率和阻尼比可通过最小二乘拟合求出:

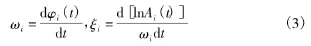
图5 IEMD方法得到的7个IMFs

4 实验验证

为了比较EEMD和IEMD方法的分解效果，利用实验室一个7层、2跨×1跨的钢框架缩尺模型进行比较分析(如图1所示)。该模型平面尺寸为0.4m×0.2m，高1.4125m。框架构件采用热轧300W级钢材(fy=300MPa)。其截面性质如表1所示。试验时在模型顶层中跨处进行激振，每层记录加速度响应，采样频率2000Hz。

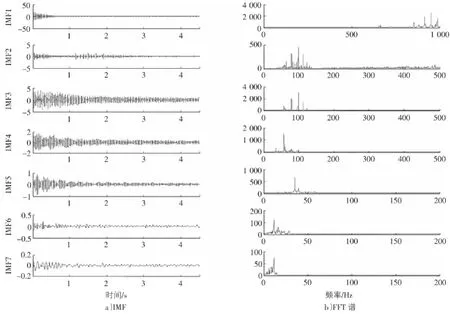
图6 EEMD方法得到的部分IMFs和与各个IMF相对应的FFT谱

利用经典EMD对实测的加速度进行分解(如图2所示)，得到12个IMFs和一个余项，FFT频谱图见图3。前7阶IMFs如图4所示。从图4中可以看到，IMF6和IMF7中存在明显的模态混叠现象。分别利用IEMD和EEMD对该实测加速度信号进行分解，得到的部分IMFs如图5，图6所示。

从图5中可以看出，该改进方法成功将此待分析信号分解成7个本征模函数，且各IMF很好地满足了单一组分的定义，不存在模态混叠及虚假模态的现象。

从图6中可以看出，EEMD方法同样可以避免模态混叠现象的发生，从图6的右部分FFT频谱图可以看出，最先得到的3个IMFs中，IMF1是添加的白噪声的残余，IMF2和IMF3中存在模态混叠的现象。这主要是因为经典EMD自身存在的缺陷，即经典EMD无法成功分离窄带信号。从图6中FFT频谱还可以发现EEMD存在能量泄露的问题，IMF6的部分能量泄露到了IMF7中，因此在后面结合HT进行模态参数识别时，将IMF6+IMF7作为一个单模态组分进行分析。同时将最先得到的3个IMF予以剔除。将经典EMD，EEMD和IEMD分解得到的IMFs进行HT变换得到的频率的识别结果如表2所示，得到的Hilbert谱如图7，图8所示。

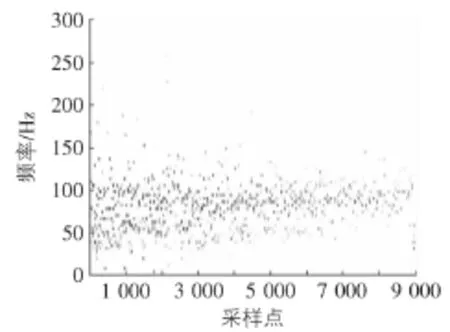
图7 EEMD+HT方法得到的Hilbert谱图

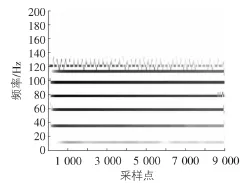
图8 IEMD+HT方法得到的Hilbert谱图

表2 不同方法的频率识别结果比较 Hz

比较图7，图8可以看出，EEMD方法得到的Hilbert谱可读性不高，频率分布很乱，即EEMD方法对经典EMD方法得到的Hilbert谱改进不大。从图8则可以看出，IEMD得到的Hilbert谱结果一目了然，图中清晰地展示了7个频率带，可读性高。比较表2可以看出，两种改进方法都在一定程度上改进了经典EMD的识别结果。其中IEMD+HT的识别结果最好，成功识别出结构的前7阶频率和阻尼比。EEMD+HT的识别结果次之，该方法只识别出了前三阶模态参数。

5 结语

本文中提到的两种主要的EMD改进方法EEMD和IEMD，在一定程度上都可以避免经典EMD方法中存在的模态混叠的问题，并通过一个实验室钢框架模型进行实验验证了两种方法的有效性。比较研究发现IEMD方法需要先验知识，在一定程度上牺牲了EMD良好的自适应性，而EEMD方法则不需要任何先验知识，分解过程完全是自动的，很好的保持了EMD方法本身良好的自适应性，但该方法需要后处理。然而，每种方法都有其优缺点和它各自的适用范围。因此，问题的关键是如何选择合适的方法来解决实际问题。本文的比较研究为此提供了一定的参考。

［1］Huang N E，Shen Z，Long S R.A new view of nonlinear water waves:the Hilbert spectrum［J］.Annu.Rev.Fluid Mech，1999，31(10):417-457.

［2］Yang J N，Lei Y，Lin S，Huang N.Hilbert-huang based approach for structural damage detection［J］.Journal of Engineering Mechanics，2004，130(1):85-95.

［3］Z.K.Peng，Peter W.Tse，F.L.Chu.An improved Hilbert-Huang transform and its application in vibration signal analysis［J］.Journal of Sound and Vibration，2005(286):187-205.

［4］Yang W.X.Interpretation of mechanical signals using an improved Hilbert-Huang transform［J］.Mechanical Systems and Signal Processing，2008(22):1061-1071.

［5］Bao C.X.，Hao H.et al.Time-varying system identification using a newly improved HHT algorithm［J］.Computers and Structures，2009(87):1611-1623.

［6］J.N.Yang，Y.Lei，S.Pan，N.Huang.System identification of linear structures based on Hilbert-Huang spectral analysis，Part I:normal modes，Earthquake Eng.Struct.Dyn，2003，32(9):1443-1467.

［7］Wu Z.H.，Huang N.E..Ensemble empirical mode decomposition:a noise-assisted data analysis method［J］.Advances in A-daptive Data Analysis，2009(1):1-41.