基于粗糙集理论的训练器材消耗影响因素分析

张汇锋， 张永杰， 冯 诚， 赵 明， 陈 毓

（1.中国人民解放军92724部队，山东 青岛 266109；2.海军航空工程学院 山东 烟台 264001）

训练器材作为教学训练保障的重要组成部分，器材的配备是否充裕将对教学水平的完成和发挥产生直接的影响。研究影响器材消耗的影响因素，对后续制定相关的保障策略，减少器材的消耗有着至关重要的作用。粗集理论是处理不完整性和不确定性的新数学理论，其最大的特点就是利用数据本身所提供的信息，不需要任何附加信息或先验信息或先验知识，在保持知识库分类能力不变的条件下，删除不相关或不重要的信息，降低信息冗余。本文以某种训练器材为例，基于粗糙集的理论基础，将影响训练器材消耗的相关因素用粗糙集方法进行预处理，简化影响因素，排除冗余，找出主要因素。

1 粗糙集理论

粗糙集（Rough sets）理论是波兰学者Pawlak于1982年提出的一种研究不精确、不确定性知识的数学工具，能有效的分析和处理不精确、不一致、不完整等各种不完备信息；能在保留关键信息的前提下对数据进行化简并求得知识的最小表达；能识别并评估数据间的依赖关系，揭示出概念简单的模式；能从经验数据中发现隐含知识，揭示潜在的规律[1-2]。

给定一个对象论域U，对于任何子集X⊆U可称之为一个U中的概念或范畴，它们构成了特定论域U的分类。其中，Xi⊆U，Xi≠Φ；Xi∩Xj=Φ，当 i≠j，i=1，2，…n；且∪Xi=U。

知识系统通常处理的是U上的分类族。一个U上的分类族，定义为一个U上的知识库。这样，知识库就是表达一个智能系统的各种基本分类方式的集合。常用等价关系替代分类，因为这两个概念完全可以互相替代。

若R是U上的划分R={X1，X2，…Xn}表达的等价关系，（U，R）称为近似空间，U/R是 R（或 U的分类）的所有等价类族。用[X]R表示子集X属于R的一个范畴，且R包括元素 x∈U。

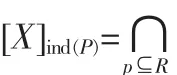
设R是一个等价关系族，且r⊆R，若有

则称r在等价关系R中是可以省略的，否则为不可省略的。

设 Q⊆P，Q 是独立的，且 IND（Q）=IND（P），则称 Q 是等价关系族P的一个约简（Reduction），记为red（P）。在P中所有不可省关系的集合称为等价关系族P的核 （core），记为core（P）。它是表达知识必不可少的重要属性集。由此可以得到，知识约简与核的关系是，约简集red（P）的交集等于P的核[3]，即

2 影响训练器材消耗数量的因素分析

很多因素能够影响训练器材消耗数量的多少，而每种因素对训练器材消耗的影响程度也各不相同。但归纳总结目前对训练器材消耗造成影响的因素可以分为可定量因素和可定性因素两大类。

通过实际调研、考察，参阅有关文献中提到的影响训练器材消耗的因素，得出主要的可定量分析的影响如图1所示。

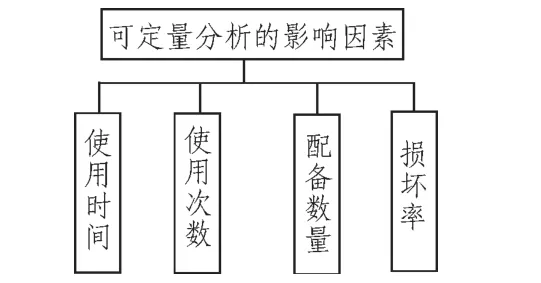
图1 训练器材消耗可定量分析的影响因素Fig.1 Quantitative analysis factors of training equipment consumption influencing factors

这些可定量分析的影响因素可归纳为：

1）使用时间T，训练器材的年使用时间；

2）使用次数Y，训练器材的年使用次数；

3）配备数量G，即该单位的器材总数量。

4）损坏率N，器材在搬运、装配和维修时或者在训练过程中由于人为差错、操作不当引起的损坏。

其次，在众多影响训练器材消耗的因素中，包含着一些难以直接用数值方法进行表述的影响因素，我们将这些影响因素归结为可定性分析的影响因素。同样，训练器材消耗中需要考虑的这些可定性分析的影响因素如图2所示。

图2 训练器材消耗可定性分析的影响因素Fig.2 Qualitative analysis factors of training equipment consumption influencing factors

在数据处理过程中对这些影响训练器材消耗的可定性分析因素转换成可定量分析的指标进行量化，并解释为：

1）丢失概率W，器材由于人为的误拿误放，管理不慎，造成训练器材的丢失，从而造成器材的消耗数量增加；

2）训练水平较差的学员所占的比例F，学员训练水平的高低，学习状况的好坏，对器材的使用熟练，爱护程度必定会对器材的消耗产生不同的影响。学员的训练水平的高低不仅与学员的年级、训练时间长短有关，而且和学员的心里素质及对器材的爱护意识也有很大关系；

3）教学水平较差的教员所占的比例J，教员的教学水平，对训练器材的熟悉程度，都会对训练器材消耗产生不同的影响，教员水平越高，对训练器材的使用熟悉程度越高，训练器材发生故障就会越少，消耗也就越少；

4）高强度集中训练课程所占的比例X，高强度集中训练课程会造成训练器材的使用频繁，强度增大，易造成器材的疲劳，容易导致故障，产生消耗。

5）存放环境D，不同的存放环境具有不同的温度、湿度、风吹日晒等外部条件，会对器材的消耗产生不同的作用。本文把存放环境分为2种情况，分别为：室内、室外，为分析的方便起见，这2种情况分别为1、2来代替。另外由于每种器材存放时有无保护措施的不同，又将其分为有保护措施存放、裸露存放，并分别用A、B来表示。

6）训练器材保养水平M，训练器材的日常保养水平也会影响训练器材的故障和消耗，如储存条件，是否按照规定存储方式存储，是否有定期检查和定期维护等。

3 基于属性约简的训练器材消耗影响因素分析

以具体器材为例阐述粗糙集在器材消耗影响因素分析中的应用过程，某训练单位编号010的训练器材2002-2012年的影响消耗因素数据整理如表1所示，所有影响因素构成属性集合{T，Y，G，W，F，J，X，D，N，M}。

表1 训练器材010消耗数量影响因素统计Tab.1 Statistic of training equipment 010 consumption influencing factors

训练器材消耗影响因素集合为 R={T，Y，G，W，F，J，X，D，N，M}， 2002 年到 2012 年的历史数据为集合 U={1，2，3，4，5，6，7，8，9，10，11}，对 R 中的属性设立阈值，超过或等于阈值的记为1，小于阈值的记为0[4-5]，其中T的阈值设为248，Y的阈值设为208.6，G的阈值设为 19.8，W的阈值设为 11.1%，F的阈值设为 12.1%，J的阈值设为 12.6%，X的阈值设为55.68%，N的阈值设为5.9%，M的阈值设为86%。根据上述阈值及处理方法对010号训练器材消耗影响因素统计表中的数据做处理得到属性值表2，如下所示。

表2 训练器材010消耗数量影响因素属性值Tab.2 Attribute values of training equipment 010 consumption quantity influence factors

由表2可知L、D各自的属性值相同，说明每年的装机数量、机场的地理位置是恒定的，对故障数量的变化不会有太大影响。根据粗糙集理论可以把它去掉。同时属性T、Y的值相同，所以只保留一个，假设保留T，删除Y。得约简属性值表3。

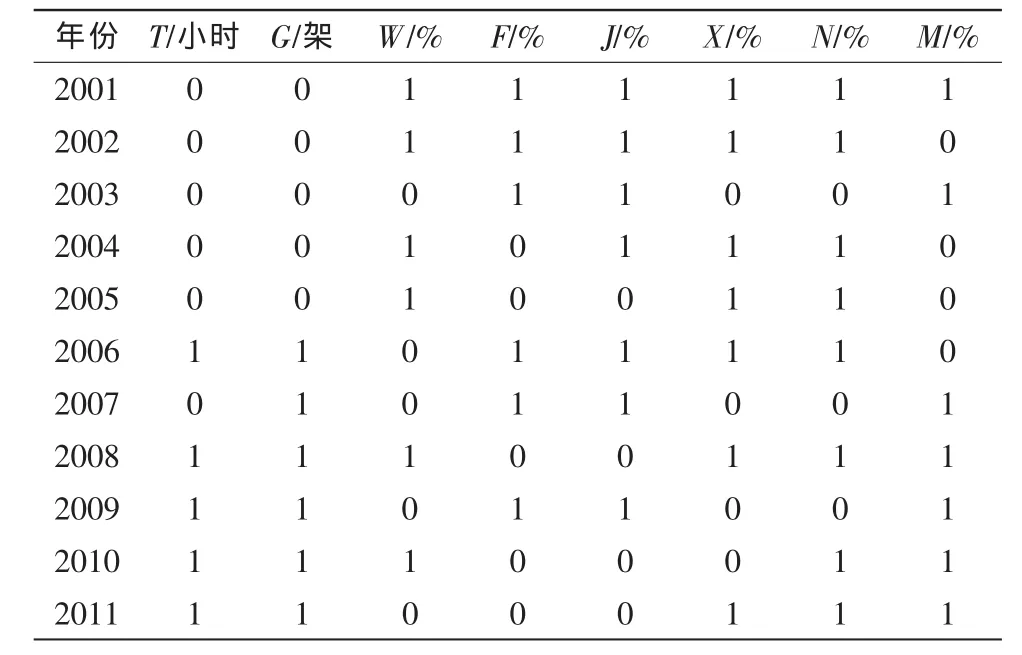
表3 训练器材010消耗数量影响因素属性值约简表Tab.3 Attribute value reduction of training equipment 010 consumption quantity influence factors

由表3可得到初步约简后的影响因素集 R1={T，G，W，F，J，X，N，M}，U={1，2，3，4，5，6，7，8，9，10，11}，根据粗糙集理论可以划分出如下的等价类[6]：

关系IND（R1）有下列等价类：

可得，以上属性 N 可省，而 T，G，W，F，J，X，M 不可省。 这样就把原来10个因素减为了7个。

4 结 论

通过上述分析，利用粗糙集知识约简能够消除干扰，从众多训练器材消耗影响因素中较为快速准确的找到主要影响因素，为训练器材保障提供了一种新的决策方法。本文利用粗糙集的数据分析与处理能力，对输入因素集进行约简，简化了数据输入量，其基本思想具有很强的推广性，适用于多因素问题。

[1]Pawlak Z.Roughsets[J].International Jourmal of Computer and Information Sciences，1982（11）：341-356.

[2]Pawlak Z.Rough sets and decision analysis[C]//In:Rough Sets and Web-Based Systems in Decision Support Processing，2000：132-144.

[3]王国胤，姚一豫，于洪.粗糙集理论与应用研究综述[J].计算机学报，2009，32（7）:1229-1246.

WANG Guo-yin，YAO Yi-yu，YU Hong.Research of the rough set theory and application [J].Chinese Journal of Computers，2009，32（7）:1229-1246.

[4]高尚.基于Rough集理论的神经网络的武器系统参数费用模型[J].系统工程理论与实践，2003，23（4）：52-55.

GAO Shang.Neural network weapon system parameter cost model based on Rough set theory[J].Systems Engineering Theory and Practice，2003，23（4）:52-55.

[5]旷海兰，刘新华，陈中，等.粗糙集理论在电力系统数据挖掘中的应用研究[J].衡阳师范学院学报，2006，23（3）:70-72.

KUANG Hai-lan，LIU Xin-hua，CHEN Zhong，et al.Rough set theory in power system data mining application[J].Journal of Hengyang Normal University，2006，23（3）:70-72.

[6]马玉良.知识获取的Rough Sets理论及其应用研究[D].杭州:浙江大学，2005.