时延网络化数控系统的建模与加工性能*

张春华 李迪 翟振坤 王世勇

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

网络化控制系统(NCS)在控制器与驱动器或传感器和控制器之间构建网络，使通讯网络作为系统闭环控制的一部分.作为一类特殊的NCS，网络化数控系统的位置环反馈量与控制量通过网络传输形成闭环控制，在信息与网络技术迅猛发展的今天，网络化数控系统已经成为数控系统发展的重要方向之一.相对点对点的连接，NCS 简化了系统的布线，降低了布线和维护成本，同时，数字信号传输提高了系统的可靠性和抗干扰性.但网络的介入，也引入了时延和丢包等新的问题，使得传统控制有关时间参数的假设不再成立，例如同步控制等.对于多轴联动数控系统，网络时延的存在以及网络节点时钟的不统一还引起多轴加工的不同步.从定性的角度，这些时间相关因素的变化往往导致控制性能下降，甚至是系统的不稳定［1-2］，是NCS 设计和实施不可忽略的重要因素［3-6］，目前，针对一般意义的NCS 研究较多［7-8］，但专门针对网络化数控系统行为特性的研究较少.因此，有必要通过建模，从定量的角度分析时间参数对数控加工性能的影响机理，为网络化数控系统的设计和实施提供理论指导.

Ryu 等［8］以两轴数控系统为研究对象，建立了时延、采样周期与动态性能指标的关系模型，为数控任务实施过程中时间参数的取值提供了一定的理论依据.文献［9］基于Truetime 工具通过仿真的手段定性地分析了时延抖动和采样周期抖动等控制任务时间参数对数控加工轮廓误差的影响.文献［10］对比了控制器、传感器和执行器结点采用时间和事件触发方式时的时延值大小

随着数控系统的不断发展，多轴联动数控越来越普遍，其加工性能不仅由单个轴的控制性能决定，还依赖于多轴协同加工的性能，但时间参数对多轴网络化数控系统加工性能的影响机理鲜有报道.论文基于修正Z 变换理论建立了时延网络化数控系统的控制模型，确立了时延、采样周期与多轴加工性能指标的关系模型，分析了其对数控系统加工性能的影响机理，是网络化数控系统设计和实施的重要理论依据.

1 网络化控制系统的时间参数与修正Z 变换

传统的采样控制理论假设系统是同步控制，即采样与控制量输出发生在同一时刻，不存在时延，如图1 所示.图中h 为采样周期，ti(i =k，k +1，…)为采样时刻.对于NCS，由于多路信号共享有限的网络资源导致时延不可避免，因此，上述假设不再成立.

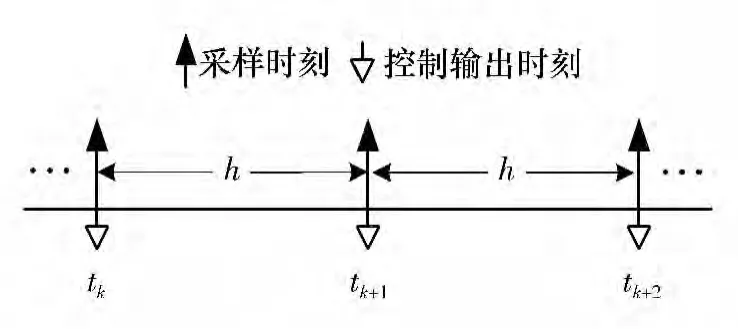
图1 理想采样控制模型Fig.1 Ideal sampled-data control model

定义1 时延及其抖动:时延是输入-输出时延的简称，指从采样时刻到控制量输出时刻之间存在的时差，用 表示，i(i =k，k +1，…)表示不同执行周期的时延，如图2 所示.时延的存在使得采样与对应的控制输出不再发生在相同的时刻，即同步控制不成立;时延抖动是指在控制任务的各个执行周期，时延值不为常数，存在着时延的变化;相对时延是指时延与采样周期的比值，用l 表示，l= /h.

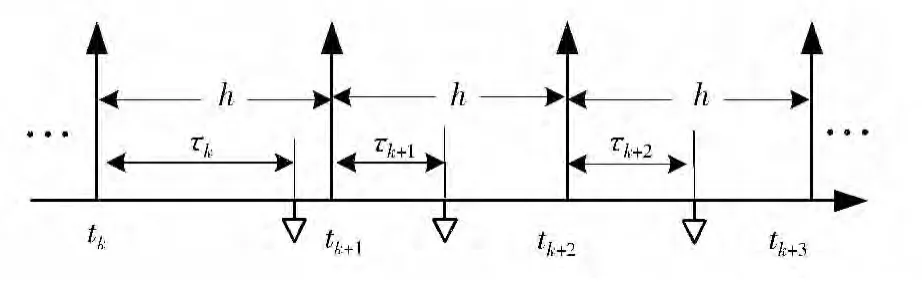
图2 控制任务的时间参数Fig.2 Time parameters of control tasks

定义2 修正Z 变换:在计算机控制系统中，离散序列f(kh)的Z 变换可以表示为

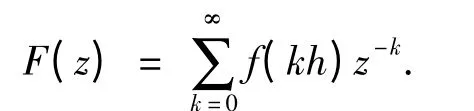
修正Z 变换是Z 变换的一种延伸［11］，可以实现非同步控制系统的Z 变换，表示为

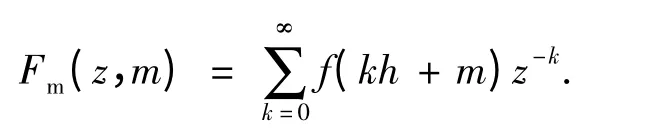
式中，m 为时延参数，0≤m ＜1，m=1-l.

2 考虑时延因素的网络化数控系统模型

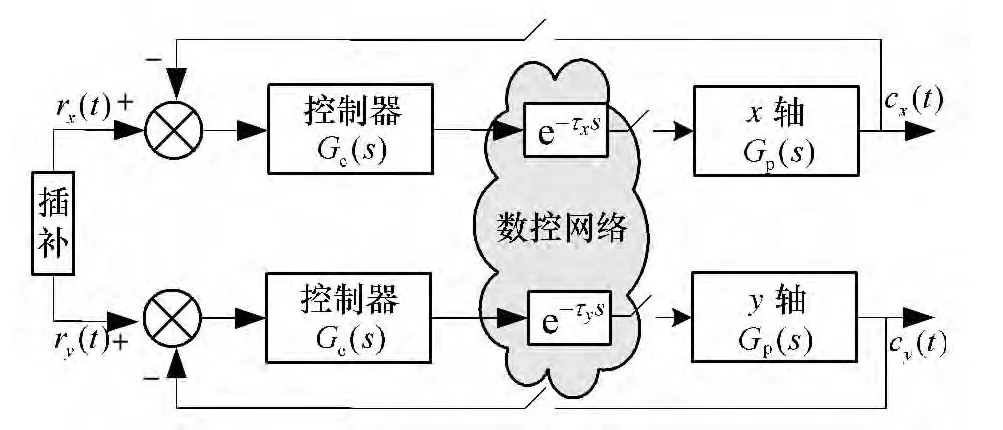
图3 具有网络时延的两轴CNC 系统框图Fig.3 Block diagram two-axis CNC system with networkedinduced delay

数控系统的单个轴可用二阶系统描述:

式中，K 为比例增益，a 为时间常数的倒数.当数控系统两个轴的结构和参数完全匹配，两个轴将具有相同的模型，只是网络诱导时延的取值不同，下面以x 轴为例(并略去下标x)建立具有时延的数控模型.采用比例控制，即Gc(s)=Kp，系统的开环传递函数Go(z)为

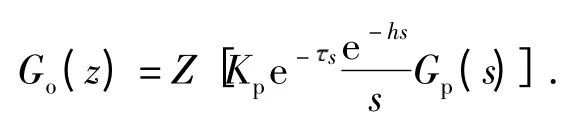
假设时延小于采样周期，即0 ＜ ≤h，基于用修正Z变换理论，Go(z)表示为

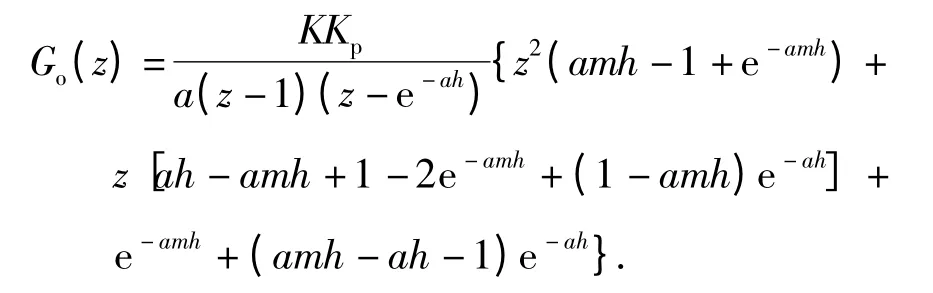
式中，m=1- /h.数控系统的采样周期一般为毫秒级甚至微秒级，且时延 小于采样周期，对上式采用近似≈1 +a［8］，且令P=e-ah，E=1 +a，则

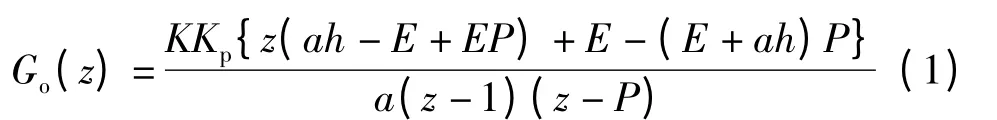
系统的闭环传递函数Φ(z)为

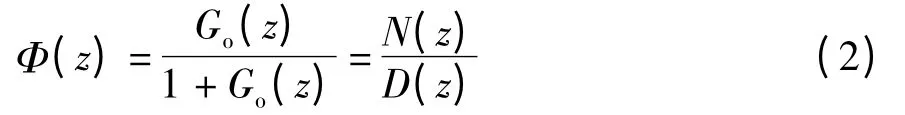
式中，N(z)=Kp{z(ah-E+EP)+E-(E +ah)P}，D(z)=az2+z(aKKph-KKpE +KKpEP-aP-a)-(aKKph+KKpE-a)P-KKpE.

由上面的建模过程可知，数控系统采样模型(2)包含两个时间参数，即采样周期h 和时延 ，一旦控制算法确定，在网络化数控任务的实施和运行阶段，数控系统的性能完全由两个时间参数的实际大小决定.

3 数控系统加工性能分析

轮廓误差、动态性能常常作为数控系统加工性能的衡量指标，建立采样周期、时延与其的关系模型是定量分析时间参数对数控加工性能影响机理的前提.

3.1 动态性能

超调量是控制系统动态性能衡量的主要指标，但采样控制系统的超调量一般只给出了定性的结论，时延的存在导致超调量的理论分析更加困难.文献［8］假设系统不存在零点，通过离散域到连续域的映射，建立了时延与超调量的关系模型，但由式(2)可知，系统实际存在零点，本节将不基于上述假设，通过一定的数学变换建立时间参数与超调量的理论模型.

根据式(2)，数控系统阶跃响应的拉氏变换(仍以x 轴为例)为

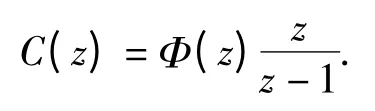
令

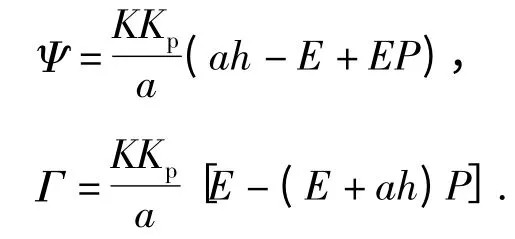
则C(z)表示为

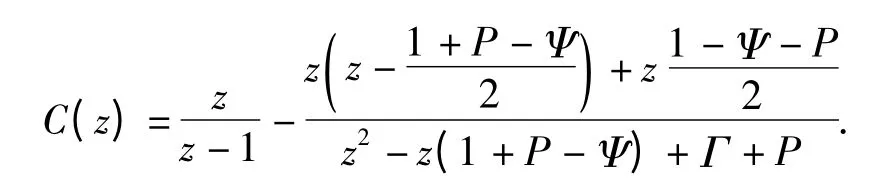
通过数学变换，得

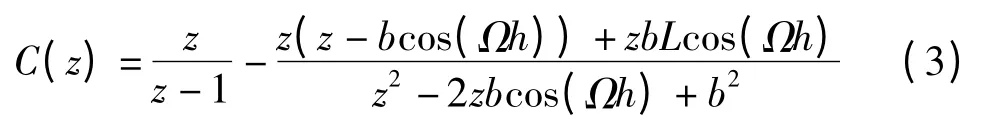
式中，b2=Γ+P，cos(Ωh)=(1+P-Ψ)/2b，sin(Ωh)=

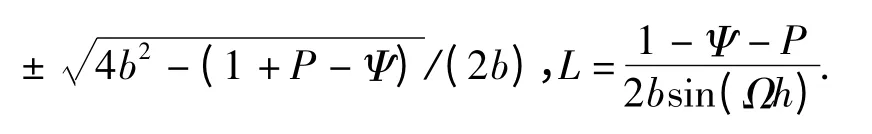
对式(3)应用Z 反变换，求得数控系统的阶跃响应:

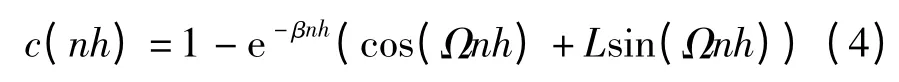
式中，β=-ln(b)/h.

由于超调量不一定正好在采样点出现，因此应用连续系统的阶跃响应［12］

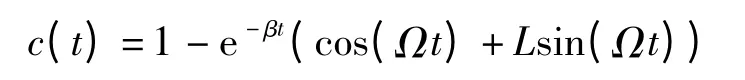
求出超调量

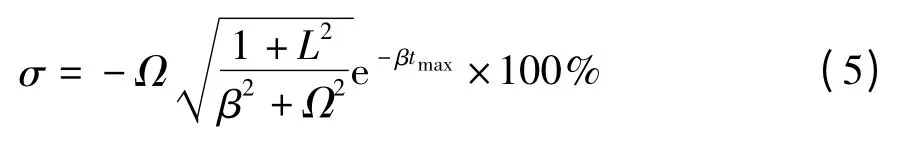
式中，tmax为峰值时间，表示为

当参数Kp=93.56，a =55.34，K =0.3 时，采样周期、相对时延与超调量的关系如图4 所示，由图可知:时延的存在使数控系统的超调量增大;时延和采样周期越大，系统的超调量也越大.

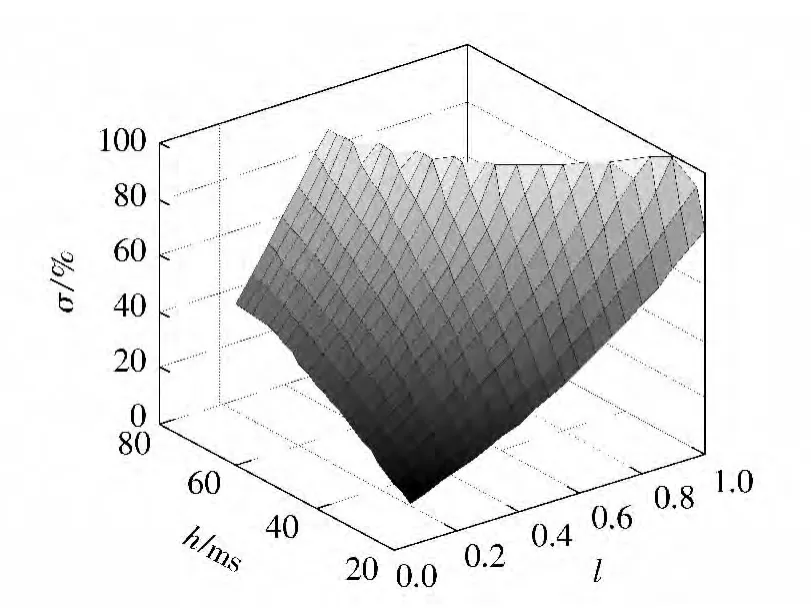
图4 采样周期和相对时延对超调量的影响Fig.4 Influence of sampling periods and relative delays on overshoots

3.2 稳态轮廓误差

数控系统进行圆加工时，x、y 轴的输入分别为

rx(t)=Rcos(ωt)，

ry(t)=Rsin(ωt).

式中，R 为圆的半径，ω 为圆加工的角频率.

3.2.1 轮廓误差模型

圆加工时，数控系统的输入为简谐信号，将z =ejω代入式(2)，系统的幅值增益Mi(i =x，y)和相位差φi:

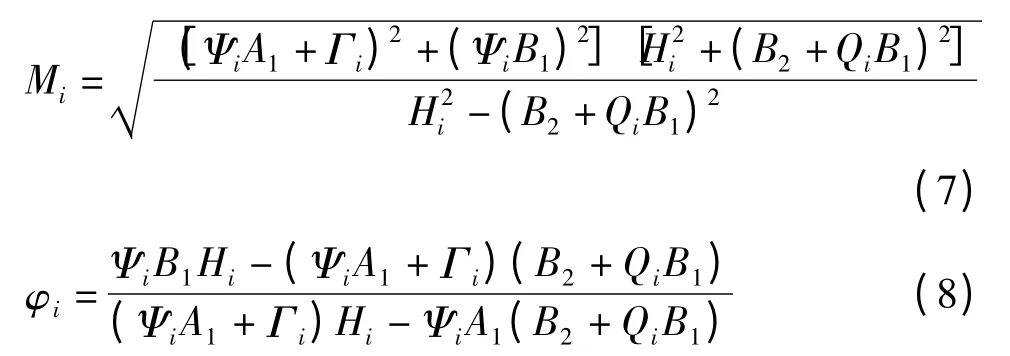
式中，A1=cos(ωt)，A2=cos(2ωt)，B1=sin(ωh)，B2=sin(2ωh)，Hi=A2+QiA1+Γi+Pi，Qi=Ψi-1-Pi，Pi、Ψi和Γi的含义分别与3.1 节中的P、Ψ 和Γ 的含义相同.

各轴在采样时刻的稳态输出分别为:

cx(nh)=RMxcos(ωnh+φx)，

cy(nh)=RMysin(ωnh+φy).

式中，nh 表示采样时刻，n=1，2，3，….

因此，圆加工的径向轮廓稳态误差ε 为

相对径向轮廓误差为

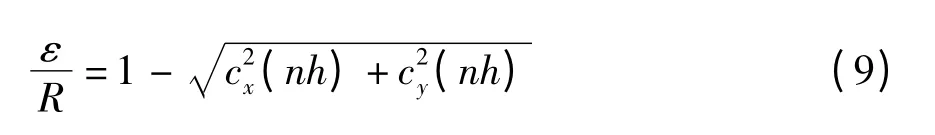
当两轴时延大小相同，即两轴完全同步时，相对径向轮廓误差表示为

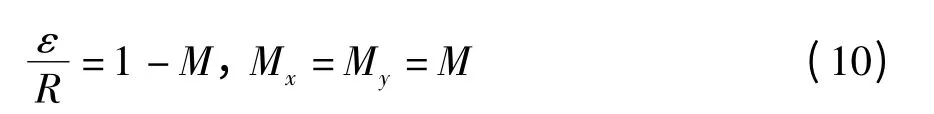
3.2.2 仿真分析

仿真模型的参数Kp=93.56，a =55.34，K =0.3.整个圆加工的轮廓误差采用误差积分指标(IAE)衡量，即

下文提到的”轮廓误差”的含义等同于式(11).在没有特别说明的情况下，x 轴和y 轴的时间参数取值相同，且仿真中的参数取值是针对单个轴而言.针对不同的影响因素，仿真分析和结果如下.

(1)采样周期和时延的大小.当时延 =0.1，0.2，0.3，0.4，0.5 ms，采样周期h =0.5，1.0，1.5，2.0 ms时，根据模型(10)，圆加工的轮廓误差如图5 所示.由图可知，采样周期和时延越大，轮廓误差越大.

当仅关注时延的影响，从误差中去除采样对轮廓误差的影响时，仅由时延引起的轮廓误差IAE'为

IAE' =IAEd-IAE0.

式中，IAEd为时延数控系统的轮廓误差，即图5 所示的误差，IAE0为无时延的轮廓误差.如表1 所示，相同时延所引起的轮廓误差IAE'的大小仍与采样周期h 有关，且h 越大，相同的时延导致的轮廓误差越大，因此采样周期的选择十分重要.

图5 时延和采样周期对轮廓误差IAE 的影响Fig.5 Influence of sampling periods and delays on contour error IAE

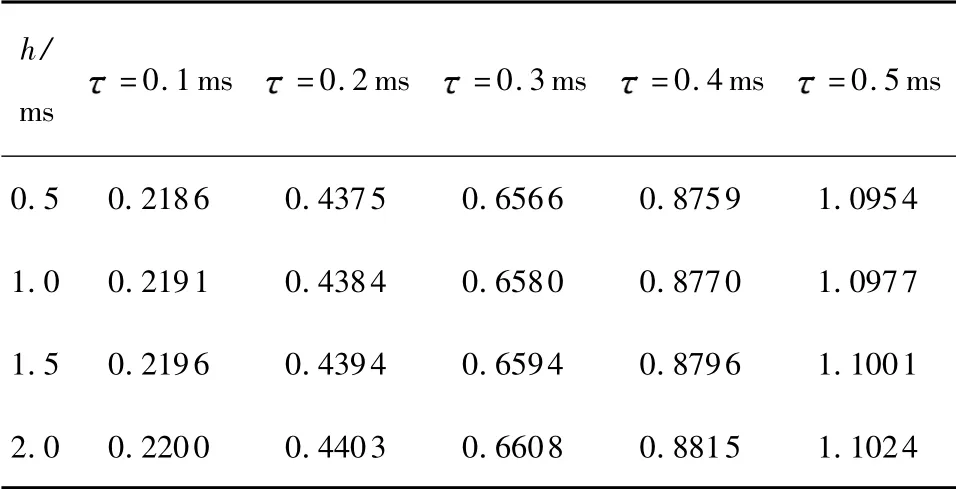
表1 仅由时延引起的轮廓误差IAE'Table 1 Circle contour error IAE' induced only by delays

(2)抖动时延.对如下的抖动时延与常数时延进行对比仿真:抖动时延J 服从［0max］上的均匀分布，时延的均值=max/2，当用相对时延lJ来描述，等同于lJ服从［0，lmax］(lmax=max/h)上的均匀分布，均值=lmax/2;常数时延与抖动时延的均值相等，即=(或l0=lJ).根据模型(10)，得到的仿真结果见表2.以h=2 ms 为例，lJ分别服从［0，0.4］、［0，0.8］上的均匀分布(等同于 J 分别服从［0，0.8］ms、［0，1.6］ms 上的均匀分布分别为0.2、0.4，得到IAE 分别为3.5296 和4.4167;对应的常数相对时延l0=0.2 和0.4 时，IAE 分别为3.5288 和4.4138，小于抖动时延的误差.图6 为h =2 ms=0.45 时抖动时延和常数时延加工圆的轮廓示意图.由图6和表2 可知，抖动时延比常数时延引起更大的轮廓误差，在实际中增加了工件的表面粗糙度.

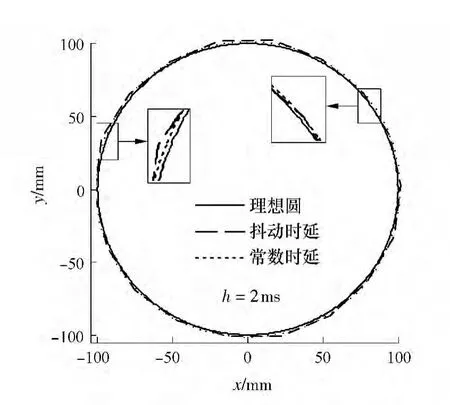
图6 均匀分布时延与常数时延圆加工轮廓对比Fig.6 Circle contour comparison between uniform-distributed and constant delays

表2 常数时延与均匀分布时延的轮廓误差Table 2 Circle contour error comparison between uniform-distributed and constant delays

(3)两轴加工不同步.多轴加工的不同步实际是由于各轴具有不同的时延导致控制输出的时刻不同，不同步加工的轮廓误差将通过式(9)求得.为了对同步和不同步情况下的轮廓误差进行对比，定义两轴数控的时延和lsum=lx+ly(lx和ly分别为x、y轴的相对时延).仿真时同步和不同步情况下的时延和lsum相等，但两轴同步时，lx=ly=lsum/2;两轴不同步时，lx=10%，ly=lsum-lx.图7 示出了h =2 ms 时的轮廓误差.由图可知，相对于两轴同步的情况，两轴不同步引起了更大的轮廓误差，且随着不同步的加剧，轮廓误差增大.

(4)加工角频率.h =0.5 ms，加工角频率ω =10，15，20 rad/s 时，根据式(10)，轮廓误差如图8 所示.显而易见，加工角频率的增大将放大网络化数控系统的轮廓误差，因此高速加工更应关注时间参数对加工性能的影响.

图7 两轴同步与不同步加工的轮廓误差IAEFig.7 Circle contour error IAE comparison between synchronous and asynchronous contouring

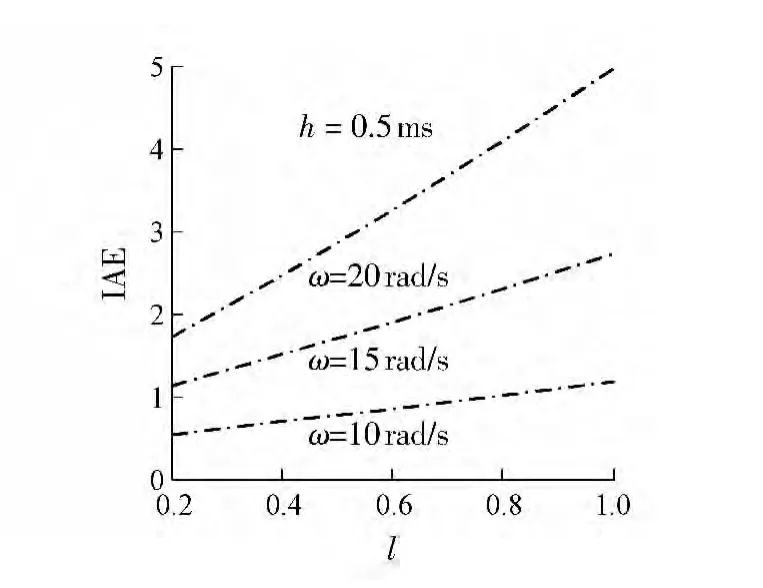
图8 圆加工角频率对轮廓误差的影响Fig.8 Influence of angular frequency on circle contour error

4 结论

文中通过建立时延网络化数控系统模型，确立关键时间参数(采样周期和时延)与数控系统超调量、轮廓误差的关系模型，从理论和仿真的角度深入地分析了时间参数对数控系统加工性能的影响机理:时延和时延抖动降低了数控系统的加工性能，时延和采样周期越大，系统的加工性能越差;与时延相比，采样周期对圆的加工性能影响更明显;多轴加工的不同步恶化了圆的加工性能;增大了圆的加工进给角频率，放大了轮廓误差，高速加工更应关注时间参数对数控系统加工性能的影响.

［1］Kalman R E，Bertram J E.A unified approach to the theory of sampling systems［J］.Journal of the Franklin Institute，1959，5(267):405-436.

［2］Kushner H J，Tobias L.On the stability of randomly sam-pled systems［J］.IEEE Transactions on Automatic Control，1969，14(4):319-324.

［3］Ray A，Halevi Y.Integrated communication and control systems:part I-analysis，and part II-design considerations［J］.Journal of Dynamic Systems，Measurements and Control，1988，110(4):367-381.

［4］Wittenmark B，Nilsson J，Törngren M.Timing problems in real-time control systems［C］∥Proceedings of the American Control Conference.Washington:IEEE，1995:2000-2004.

［5］Gupta R A，Chow M.Networked control system:overview and research trends［J］.IEEE Transactions on Industrial Electronics，2010，57(7):2527-2535.

［6］Zhang L，Gao H，Kaynak O.Network-induced constraints in networked control systems—a survey［J］.IEEE Transactions on Industrial Informatics，2013，9(1):403-416.

［7］Richard J.Time-delay systems:an overview of some recent advances and open problems ［J］.Automatica，2003，39(10):1667-1694.

［8］Ryu M，Hong S.Toward automatic synthesis of schedulable real-time controllers［J］.Integrated Computer-Aided Engineering，1998，5(3):261-277.

［9］李迪，万加富，叶峰，等.软数控实时任务的时间特性对加工精度的影响［J］.华南理工大学学报:自然科学版，2009，37(2):1-5.Li Di，Wan Jia-fu，Ye Feng，et al.Effect of time characteristics of software NC real time tasks on manufacturing accuracy［J］.Journal of South China University of Technology:Natural Science Edition，2009，37(2):1-5.

［10］云利军.网络化运动控制系统行为特性的研究［D］.天津:河北工业大学电气工程学院，2006:31-44.

［11］Jury E I.Theory and application of the Z-transform method［M］.New York:Krieger Pub Co.，1973:15-19.

［12］Koren Y，Bollinger J G.Design parameters for sampleddata drives for CNC machine tools［J］.IEEE Transactions on Industry Applications，1978，IA-14(3):255-264.