超低信噪比下基于阵列式Duffing振子的频谱感知系统*

贾琼 李兵兵

(西安电子科技大学 通信工程学院，陕西 西安 710071)

作为认知无线电中最重要的核心环节，频谱感知(频谱检测)技术近年来受到国内外学者的广泛关注.通过频谱感知技术，认知用户能在不干扰授权用户的前提下发现并利用未被占用的频谱资源，因而大大提高了频谱利用率.然而在低信噪比环境下，检测过程中往往存在误检或漏检的情况，错误的判决结果将会对授权用户带来干扰.因此研究在低信噪比环境下易于实现且检测精度较高的频谱检测算法对于认知无线电的实现具有重要意义.

关于单用户频谱检测算法，早期的研究一般都集中在能量检测、匹配滤波检测、特征检测这3 种方法上.文献［1］较为详细地介绍了3 种检测方法的检测原理并简要分析了各自的性能.其中能量检测在低信噪比(信号与噪声的功率比)环境下性能较差;而匹配滤波法由于需完全已知先验信息，不易实现;特征检测法相对性能较好，但是过程复杂.因而一直以来，获得一种性能好且易于实现的频谱感知方法是国内外学者们共同的研究目标.近年来，一些学者通过对3 种方法进行改进取得了一些新的研究成果.文献［2］将循环平稳特征和能量检测结合，提出了基于循环谱能量的自适应频谱检测算法，相较于原来单一的方法检测性能有所提升;而文献［3］则利用压缩感知技术和循环平稳特征检测结合，研究了一种新的宽带频谱检测算法，但是计算过程较为复杂;文献［4-5］则分别分析了噪声方差未知和衰落信道下的盲频谱检测算法.

虽然上述文献中提出的方法在性能上比之于早期的3 种基本检测方法而言有所提升，但是可以实现准确检测的信噪比门限也只有-10 dB 左右.而以电视广播信号为例，联邦通讯委员会(FCC)要求至少在信噪比为-18dB 的情况下实现可靠检测［6］，显然，只有在超低信噪比(＜-20 dB)环境下依然可以有效可靠检测的方法才能满足要求，而目前国内外关于超低信噪比条件下的频谱感知方法的研究鲜见报道.

20 世纪90 年代，Birx 等［7］将混沌理论应用于信号检测，通过实验验证了利用混沌振子检测微弱信号的有效性.在此基础上，众多学者对基于混沌理论的微弱信号检测进行了研究，并取得了相应的研究成果［8-12］，结果显示对于低信噪比环境下的微弱信号，利用混沌系统依然可以实现较为精确的检测.文中将混沌动力学理论与频谱感知技术结合，重点研究了在低信噪比环境下Duffing 频谱感知系统的检测性能，提出了适合实际应用的阵列式频谱检测方案，为认知无线电系统中超低信噪比环境下的可靠频谱检测提供了理论依据.

1 频谱感知系统模型

1.1 Duffing 频谱感知模型

Duffing 方程所确定的动力学系统已经被证明可以产生混沌现象，且被广泛应用于分析混沌演变特性，其一般形式如下:

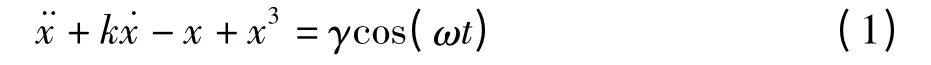
式中，x 为系统响应，k 为阻尼比，γ 为周期激振力幅值，ω 为激振力的频率，t 为时间.

基于Duffing 振子的频谱感知原理，即利用混沌系统对参数的敏感性和对噪声的免疫性，文中先通过解析或数值的方法设置合适的阈值，使得系统处于由混沌状态向大尺度周期态过渡的临界状态;然后将接收到的信号加入系统，如果信号中包含授权用户的信号，则会诱发系统状态的改变，否则系统仍然保持混沌状态;最后通过识别系统状态判断有无授权用户的存在，从而决定是否使用频段.

要实现上述检测过程，前提是必须对混沌系统的动力学演变特性有详细的了解.通过Melnikov 方法的研究可知［7］，对于固定的阻尼比，在0≤γ ＜1的范围中，当γ 逐渐增大时，会出现一个稳定的混沌状态，而当γ 继续增大超过某一阈值时，会发生鞍结分岔行为，混沌吸引子快速消失转变为大尺度周期状态.这一阈值的求解也可以通过Melnikov 方法计算得到.

因此，文中提出的基于Duffing 振子的频谱感知方法的过程如下:

(1)根据Melnikov 方法计算出式(1)所描述的系统对应的临界态参数kc、γc，然后将接收到的信号y 加入，则系统方程写成

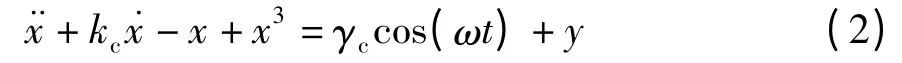
(2)识别上述系统的状态，如果系统处于大尺度周期状态，表明接收到的信号中包含有与系统周期激振力同频的授权用户信号，如果系统仍然处于混沌状态，则表明接收到的信号中只包含噪声.

频谱感知可描述为二元假设检验:

式中:s 表示授权用户的发送信号，w 表示加性高斯白噪声，且均值为0，w～N(0，σ2).

基于Duffing 振子频谱检测的判决模型如下:

即若系统处于混沌，判定假设H0成立，被测频段可用，若系统为周期状态，判定假设H1成立，频段不可用.其中，S 表示式(2)对应系统的状态.

1.2 不同频率激振力振子之间的等效转换

Duffing 系统仅仅对于与系统本身周期激振力频率相同或者相近的周期信号敏感，即对于式(4)所定义的模型只能识别频率为ω 的信号，如果要检测的授权用户信号频率为ωs(ωs≠ω)，则需要将式(1)中的激振力频率调整为ωs，通过Melnikov 方法重新计算系统临界参数kc、γc并代入式(2)中，然后根据式(4)的判决模型来完成检测，操作过程太过繁复.因此，文中引入无量纲变换系数，实现了不同频率激振力振子之间的等效转换，简化了上述过程.

在式(1)所描述的一般系统下，对于频率为ωs的授权用户信号，定义无量纲变换系数ρ =ωs/ω，并令t=ρ，则

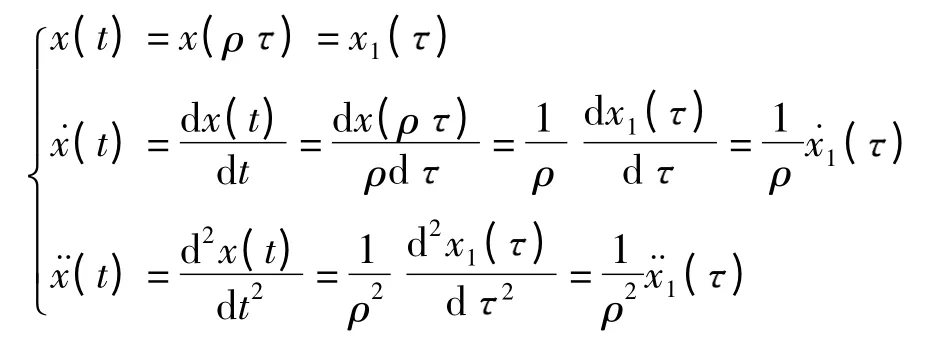
代入式(1)中并忽略角标得

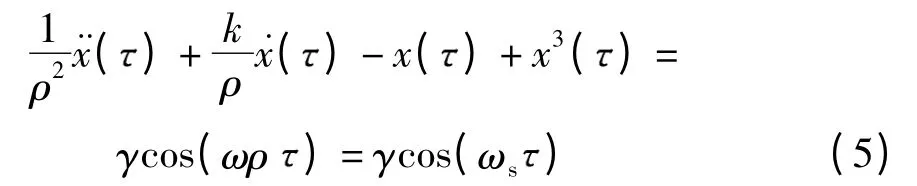
由于在上述转化过程中，无量纲系数的引入只是对系统在时间轴上进行延伸或压缩，对于系统的状态并没有影响，因此式(1)和式(5)对应的两个系统完全等效，且两者临界参数也相同.

因此，引入无量纲变换系数后，调整频谱检测模型如下:

对于不同频率的待检信号，只需要修改系统式(6)中的变换系数ρ，调整激振力频率为待测频率，然后根据式(4)进行判决即可完成检测(经过无量纲化后，式(4)中S 表示式(6)系统的状态)，无需重复计算临界参数，大大降低了复杂度.

1.3 阵列式Duffing 振子频谱感知系统

虽然式(6)对应的检测系统通过引入无量纲系数，更加便于检测不同频率的待测信号，但是在实际的频谱感知过程中，往往需要检测在一个频段范围内有无授权信号，显然，式(6)无法实现频段信号的检测.因此，需要设计能够对一个频段进行检测的频谱感知模型.基于此，文中提出了阵列式Duffing 振子频谱感知模型.

设待检测的频段为ω1～ωM，且该频段被划分成M 个信道.令Ω=［ω1，ω2，…，ωi，…，ωM］(其中ωi(i =1～M)对应于各个信道的中心频率)，以系统(6)为振子单元，根据上述频段构造由M 个振子构成的Duffing 振子阵列，M 个振子的激振力频率分别对应于M 个中心频率，然后将接收信号加入振子阵列，如果被检测的频段中有授权用户使用，则M 个振子中会有一个或多个振子转为大尺度周期态，而其他振子仍然处于混沌状态，最后通过识别各振子的状态，即可判断该频段内是否有授权用户信号.

在上述分析过程中，均没有讨论接收信号的形式.然而实际应用中，为了更加便于传输，需要经过调制等处理，而这些处理导致Duffing 系统对信号的敏感度降低，因而会影响最终的检测性能.因此，对于接收到的信号需要进行相应的预处理.下面以授权用户信号为BPSK 信号为例进行分析.

对于BPSK 信号，其一般表达式如下:

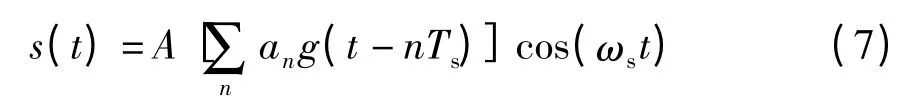
这里g(t)是脉宽为Ts的单个矩形脉冲，A 表示信号幅度，而an= ±1，分别对应二进制符号1 和0.在一个码元持续时间Ts内，

若将接收到的BPSK 信号直接加入混沌系统，则

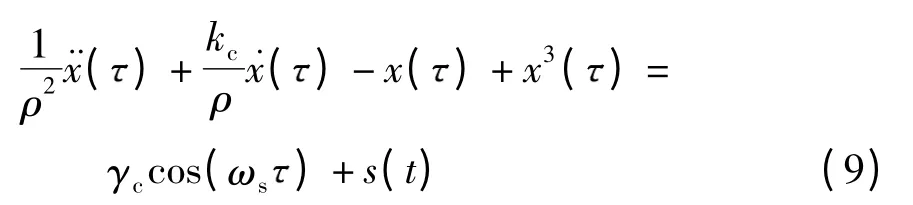
在一个码元间隔内，将式(8)代入式(9)有

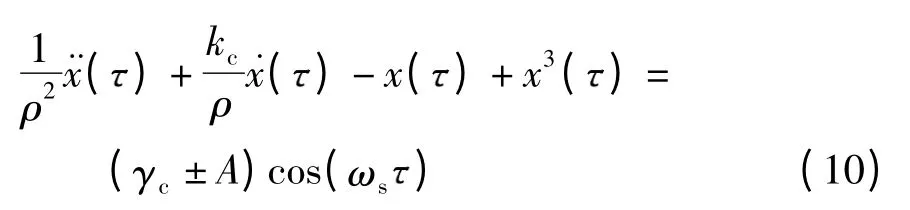
显然，只有对应的发送码元符号为1 时，将BPSK 信号加入到处于临界态的Duffing 系统才会转变为大尺度周期态，而当发送符号0 时，系统会继续保持混沌状态.可见直接将接收到的授权用户信号加入混沌系统进行检测过程中，会存在漏检的情况，因此引入预处理模块.

对接收到的BPSK 信号首先进行平方处理，然后调整系统激振力频率和无量纲系数，将预处理后信号加入系统得

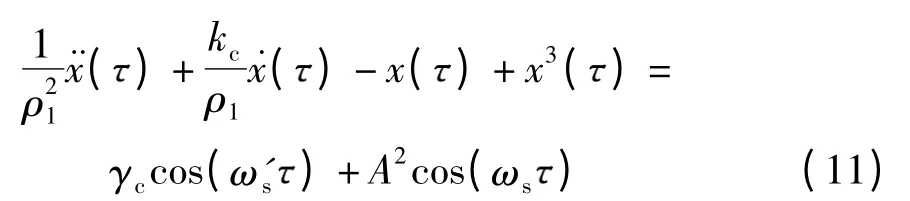
因此只需令ω's=2ωs，ρ1=2ρ，即可保证系统对于经过预处理后的BPSK 信号具有较高的敏感性，从而进行检测.可见通过引入平方预处理，避免了由于BPSK 信号本身特点所导致的误检情况，因此提高了性能.而对于其他形式的调制信号，可采用各自相应的预处理方法.

在阵列式Duffing 振子频谱检测系统中，非常关键的一个环节即识别振子的状态是处于混沌还是大尺度周期，即混沌判据.文中采用相图法与Lyapunov指数法相结合的方式来对振子阵列的状态进行识别.所提出的阵列式Duffing 振子频谱感知系统框图如图1 所示.

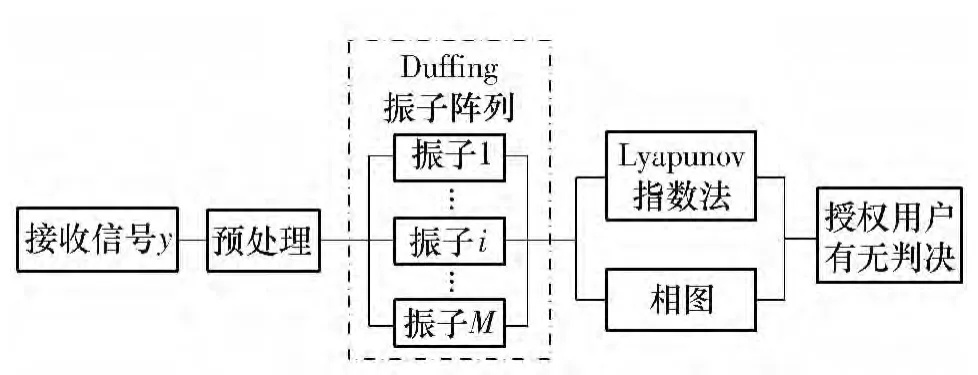
图1 阵列式Duffing 振子频谱感知系统框图Fig.1 Block diagram of array Duffing oscillator spectrum sensing system

具体工作过程为:首先将接收信号送入预处理模块，对于待检测频段ω1～ωM，如果存在授权用户信号，则信号在通过Duffing 振子阵列时，会激发其中的一个或多个振子由初始的临界状态转变为大尺度周期状态.通过Lyapunov 指数法和相图法结合的方式，对振子阵列的状态进行识别，从而可以判决接收信号中是否包含有授权信号，从而完成频谱感知.

文中提出的方法的算法复杂度源于对Duffing方程的求解，这里采用四阶龙格库塔法，对于长度为L 的接收信号，其计算复杂度为O(L3)，相比于传统的能量检测需要的计算复杂度O(L2)而言，虽然有所增加，但是其检测性能得到了很大的提升，具体的检测性能将在下一节数值分析中介绍.

2 仿真与分析

(1)由于图1 中描述的M 个振子阵列结构完全相同，区别只在于各个振子所对应的无量纲变换系数和激振力频率不同，因此先以单个振子为例，通过仿真实验验证文中提出的不同频率激振力振子之间的等效性.

设授权用户发送的信号频率100 Hz，仿真中所采用系统阻尼比k=0.5.由于文中2.3 节已经证明式(5)与式(1)描述的系统等效，而对于式(1)所描述的系统，已经有学者对其在阻尼比k =0.5、周期激振力频率ω=1 时的情况进行了研究［11］，结果表明当周期激振力幅值γ=0.826 时，系统处于由混沌向大尺度周期过渡的临界状态.根据文中结论，设置式(5)中的变换系数ρ =100，激振力频率ωs=100，则γ=0.826 一定也是式(5)对应系统的临界态参数，图2 中的仿真结果验证了这一结论.

图2(a)、(b)分别为式(1)所描述系统在ω =1时的临界态和大尺度周期态相轨迹图，激振力幅值γ分别为0.826 和0.827;图2(c)、(d)分别为式(5)所描述系统在ωs=100，ρ =100，激振力幅值分别为0.826 和0.827 时的相轨迹图，可见，经过无量纲化后，0.826 仍然是式(5)系统的临界态参数.

图2 Duffing 系统相轨迹图Fig.2 Phase portraits of Duffing system

(2)为验证文中提出方法的有效性，采用相图法和Lyapunov 指数法相结合的方式进行了仿真实验，结果表明文中的模型对于授权用户信号在超低信噪比环境下仍然敏感.设定系统参数为临界值k=0.5，γ =0.826，待检授权用户信号为载波频率100 Hz 的BPSK 调制信号，对于BPSK 信号进行平方预处理，故而设置系统的激振力频率为200 Hz.仿真中设信号幅值为0.1，信噪比为-25dB.图3、图4 分别示出了处于临界态的系统加入待测信号前后的相图以及Lyapunov 指数收敛曲线.

图3(a)为文中提出的频谱检测系统处于临界态时的相轨迹图，而图3(b)为在系统中加入包含有授权用户信号的接收信号后系统的相轨迹图，显然加入接收信号后，系统由原来的临界态迅速转变为大尺度周期态.

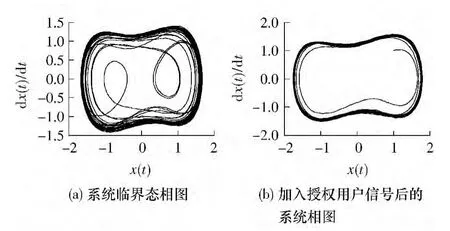
图3 系统相轨迹的变化Fig.3 Change of phase portraits of the system

文中提出的模型可转化为三维自治系统，因而有3 个Lyapunov 指数，并且一个恒为零.在采用Lyapunov 指数法对系统进行混沌识别时，只要最大Lyapunov 指数大于0，即可判定系统处于混沌状态，否则可判定系统处于大尺度周期态.图4(a)表示系统处于临界态时3 个Lyapunov 指数的收敛曲线，由图可见其中一条最终收敛在大于0 的位置，因此在加入接收信号前，系统尚处于混沌状态.而从图4(b)中明显看出，加入接收信号以后，系统转变为大尺度周期态.因此，在实际应用中，结合相图法和Lyapunov 指数法，在超低信噪比环境下也可以实现频谱检测.

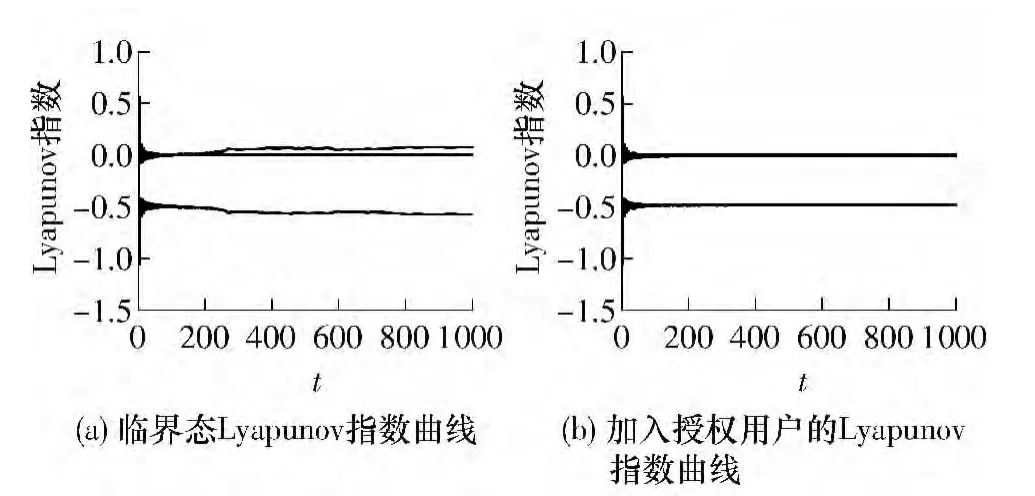
图4 系统Lyapunov 指数收敛曲线Fig.4 Convergence curves of Lyapunov exponent of the system

(3)为体现文中方法的优越性，将阵列式Duffing 振子频谱感知方法与传统的能量检测方法以及文献［2］中的循环谱能量法进行了性能对比.仿真中待检测频段为100～300 Hz，划分分成10 个信道，在σ=0.1 高斯白噪声背景下，信噪比范围为-40～10dB，采用蒙特卡洛仿真法，统计次数为105，3 种方法的检测性能如图5 所示.

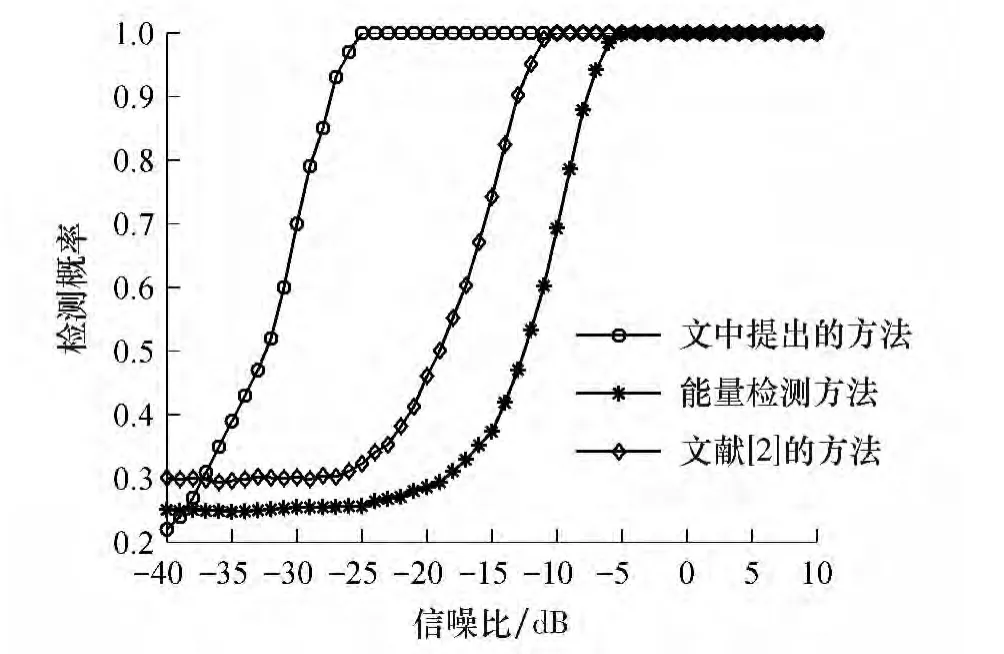
图5 3 种频谱感知方法检测性能对比Fig.5 Comparison of detection performances of three spectrum sensing methods

结果表明，传统的能量检测法在信噪比低于-5 dB后，检测性能急剧下降.文献［2］方法比能量检测方法虽然有了一定的提升，但在信噪比低于-15 dB 后检测性能较差，而文中提出的方法在信噪比达到-25 dB 时仍然保持较高的检测性能，从而实现了认知无线电中的可靠频谱检测.

3 结语

文中将混沌理论与认知无线电频谱感知技术相结合，提出了一种基于Duffing 振子的频谱检测方法.通过引入无量纲系数，建立了不同频率激振力作用下Duffing 振子之间的等效转换，其优点在于在实际应用中需要检测不同频率的授权用户信号时，无需重复计算系统的临界参数，只要通过调整无量纲变换系数，沿用原来的参数，仍然可以使得新系统处于临界状态.然后，通过预处理，建立了阵列式Duffing 振子频谱感知系统模型，为该理论的实际操作提供了解决方案.最后，通过计算机仿真，验证了方法的有效性，并且与传统的能量检测方法以及文献中的循环谱能量检测法做了对比，结果显示相较于这两种方法，文中提出的方法在检测性能方面有很大的提升，且检测过程中只需要将接收信号送入Duffing 振子系统，通过识别振子状态就可完成检测，原理简单易于实现.对于混沌理论与频谱检测的结合，目前国内外尚未有相应的研究基础，文中对于信道环境的分析也均采用较为简单的高斯白噪声信道，对于更加复杂的信道环境中混沌频谱的应用值得进一步研究探讨.

［1］Cabric D，Mishra S M，Brodersen R W.Implementation issues in spectrum sensing for cognitive radios［C］∥Conference Record of the Thirty-eighth Asilomar Conference on Signals，systems and computers.Pacific Grove:IEEE，2004:772-776.

［2］张昊晔，包志华，张士兵.基于循环谱能量的自适应频谱检测算法［J］.通信学报，2011，32(11):95-103.Zhang Hao-ye，Bao Zhi-hua，Zhang Shi-bing.Adaptive spectrum sensing algorithm based on cyclostationary spectrum energy ［J］.Journal on Communications，2011，32(11):95-103.

［3］Tian Z，Tafesse Y，Sadler B M.Cyclic feature detection with sub-Nyquist sampling for wideband spectrum sensing［J］.IEEE Journal of Selected Topics in Signal Processing，2012，6(1):58-69.

［4］沈雷，王海泉，赵知劲，等.认知无线电中基于拟合优度的频谱盲检测算法研究［J］.通信学报:2011，32(11):26-33.Shen Lei，Wang Hai-quan，Zhao Zhi-jin，et al.Blind spectrum sensing based on goodness of fit test for cognitive radio in noise of uncertain power［J］.Journal on Communications，2011，32(11):26-33.

［5］Nevat I，Peters G W，Yuan J H.Blind spectrum sensing in cognitive radio over fading channels and frequency offsets［C］∥Proceedings of 2012 IEEE Wireless Communications and Networking Conference (WCNC).Shanghai:IEEE，2012:1039-1043.

［6］Quan Z，Zhang W Y，Shellhammer S J，et al.Optimal spectral feature detection for spectrum sensing at very low SNR［J］.IEEE Transactions on Communications，2011，59(1):201-212.

［7］Birx D L，Pipenberg S J.Chaotic oscillators and complex mapping feed forward networks (CMFFNS)for signal detection in noisy environments［C］∥Proceedings of International Joint Conference on Neural Networks.Baltimore:IEEE，1992:881-888.

［8］李月，杨宝俊，林红波，等.基于特定混沌系统微弱谐波信号频率检测的理论分析与仿真［J］.物理学报，2005，54(5):1994-1998.Li Yue，Yang Bao-jun，Lin Hong-bo，et al.Simulation and theoretical analysis on detection of the frequency of weak harmonic signals based on a special chaotic system［J］.Acta Physica Sinica，2005，54(5):1994-1998.

［9］高仕龙，钟苏川，韦鹍，等.基于混沌和随机共振的微弱信号检测［J］.物理学报，2012，61(18):181501/1-7.Gao Shi-long，Zhong Su-chuan，Wei Kun，et al.Weak signal detection based on chaos and stochastic resonance［J］.Acta Physica Sinica，2012，61(18):181501/1-7.

［10］胡文静，刘志珍，厉志辉.用于微弱信号检测的改进Duffing 混沌电路性能分析［J］.电机与控制学报，2011，15(9):80-85.Hu Wen-jing，Liu Zhi-zhen，Li Zhi-hui.Weak signal detection performance of improved Duffing circuit ［J］.Electric Machines and Control，2011，15(9):80-85.

［11］魏恒东，甘露，李立萍.基于哈密顿量的Duffing 振子微弱信号检测［J］.电子科技大学学报，2012，41(2):203-207.Wei Heng-dong，Gan Lu，Li Li-ping.Weak signal detection by Duffing oscillator based on Hamiltonian ［J］.Journal of University of Electronic Science and Technology of China，2012，41(2):203-207.

［12］Qu L，Lin J.A difference resonator for detecting weak signals［J］.Measurement，1999，26(1):69-77.

［13］李含青，郭庆，李庆忠.基于迭代支持检测的分布式压缩频谱感知算法［J］.华南理工大学学报:自然科学版，2013，41(1):64-68.Li Han-qing，Guo Qing，Li Qing-zhong.Distributed compressive spectrum sensing algorithm based on iterative support detection［J］.Journal of South China University of Technology:Natural Science Edition，2013，41(1):64-68.

［14］Khattab A，Perkins D，Bayoumi M.Opportunistic spectrum access challenges in distributed cognitive radio networks ［M］∥Cognitive Radio Networks.New York:Springer，2013:33-39.

［15］Zeng Y，Liang Y C，Pham T H.Spectrum sensing for OFDM signals using pilot induced auto-correlations［J］.IEEE Journal on Selected Areas in Communications，2013，31(3):353-363.

［16］Huang G，Tugnait J K.On cyclostationarity based spectrum sensing under uncertain Gaussian noise［J］.IEEE Transactions on Signal Processing，2013，61(8):2042-2054.