多向格型微分和竞争抑制的角点检测改进方法*
2013-08-19马丽红黎剑晖谭幸均
马丽红 黎剑晖 谭幸均
(1.华南理工大学 电子与信息学院,广东 广州 510640;2.海思半导体有限公司 网络架构与系统设计部,广东 深圳 518129)
角点检测是图像目标定位和跟踪处理中的关键步骤.目前的角点检测算法主要分为4类:①基于边缘的角点检测.这类检测算法,如基于链码的检测器[1-2],一般选择曲线中具有高曲率的点作为角点.②基于梯度的角点检测.这类算法选择在多个方向上都具有低相似度的特征点作为角点,经典的梯度角点 算 法 有Harris[3]、Noble[4]和 它 们 的 改 进 算法[5-6],以及尺度不变特征转换算子(SIFT)等[7].③基于外观的角点检测.此类方法直接考察图像块是否具有角点的外观,其中一种具有代表性的检测方法是最小核心值相似区域(SUSAN)[8]算法,该算法采用圆形窗口模板,通过计算模板内相似像素的区域面积来区分角点.④概率学习辅助的角点检测.此类方法使用贝叶斯标记、决策树和支持向量机等方法来训练角点分类器[9-11].
以上算法都基于这样的事实:微分算子沿边缘方向的响应值较小,沿边缘正交方向的响应值较大,而角点在多个方向上具有显著的灰度变化并可通过测量其微分响应来确定.实际上,传统的微分算子主要表达二维图像中的水平和垂直两个方向的梯度值,而4 方向的微分算子则能更准确地检测图像角点.但是,一个点在2 个或者4 个方向上的微分值较大,并不能断定该点就是角点,因为它可能仅为图像边缘点;把8 方向的微分值融合将有助于确定真正角点.不过,因为空间位置离散,8 方向微分算子的表示、计算比较棘手,特别是在不同尺度下,检测结果差异较大.
因此,为构造沿任意方向的图像微分变换,更好地抑制锯齿边缘的伪角点,文中提出一个复合格型分解微分算子.另一方面,由于真实角点附近微分响应往往较强,特别是缓变角点附近,会在一个较小邻域内产生多个紧靠的角点,检测算法可能重复检出角点,为此文中提出一种邻域竞争抑制方法.目前,大部分算法根据邻域尺寸设置阈值来消除误检[1],文中则是根据微分响应值定义不同角点之间的相似度.
1 格型微分算子
除水平、垂直、45°和135°方向外的图像离散边缘呈锯齿状.图1(a)是一条斜率为1/2 的图像边缘,锯齿点水平、垂直和45°方向的灰度变化较大,这些点会被误判为角点.为了去掉线边缘的锯齿角点,文中基于Directionlet 小波分解原理来保证任意有理方向的线边缘不产生伪角点.根据整数格定义,Directionlet 把图像边缘分离成不相交的若干个陪集,每个陪集的点均真实分布在相同斜率的陪线上[12-13].每个陪集的像素点具有两个特点:①像素值接近,因为它们来自同一边缘;②分布在斜率相同的直线上,而且没有锯齿状斜率结构.对于水平、垂直、45°和135°方向,边缘是陪集分解的特例,它们只有一个陪集和一条陪线;其他斜率为有理数r 的图像边缘均可分离成两个或两个以上不相交的陪集.图1(a)的边缘被分离成3 个不相交的陪集,分别用虚线、实线和点线标记,如图1(b)所示,3 条陪线斜率均为1/2.

图1 图像边缘的两种表示方法Fig.1 Two representations of an image edge
1.1 格型陪线微分定义
对于r 斜率上分离的K 个陪集,每个陪集的像素点组成序列fk(n)(k =1,2,…,K)在任何尺度下都是斜率为r 的无锯齿真实直线.定义各陪线的常规微分f'k(n),各陪线微分的均值为格型陪线微分f'(n):

则可定义一个沿任意有理数方向i、斜率为ai/bi的格型微分响应矩阵Gi:

式中,Gi元素f'(n)(n =1,2,…,N)为像素点n 在方向i 的微分值,N 为图像的像素点个数.
1.2 微分方向向量表示
自然图像中存在任意方向边缘,文中采用4 对正交向量来表示格型微分的8 个方向:以待处理像素为中心,将180°角区间均等划分成8 份,任一正交方向对内的两个方向互为陪线最大梯度方向的校验子,这4 对正交向量的斜率分别为:

斜率对Λ1表示两个互为正交方向,斜率分别为0和∞,Λ1、Λ2、Λ3和Λ4的方向示意见图2(a).图2(b)是由正交向量对Λ2生成的整数格,不同的灰度方格代表不同的陪集.

图2 格型微分方向及分解示意图Fig.2 Schematic diagram of latticed differential directions and decomposition
图3 示出了对战斗机图像进行格型微分的结果.图3(a)在Λ3两个方向的微分结果为图3(b)和图3(c);图3(a)在Λ2两个方向的微分结果为图3(d)和图3(e).格型分解使微分真正地沿着有理数方向i进行.从图3(b)可以看出,边缘①上的点能在该边缘方向上获得较小微分值,边缘①的角点能在Λ2两个方向以及Λ3斜率为-1 方向上获得较大微分值.

图3 格型微分结果Fig.3 Latticed differential results
1.3 格型微分角点检测
根据Λ1-Λ4微分响应的组合以及边缘点和角点在微分响应值上的差异,定义多向格型微分算子(DLD)用于区分边缘点和角点.DLD 角点检测算法分为两个步骤:首先获取8 个方向的微分响应矩阵Gi(i=1,2,…,8),再根据矩阵Gi对角点进行判断.其判断准则是:
(1)如果图像中的某个点P(xP,yP)至少在一个微分响应矩阵中的值小于设定的阈值TV,则该点在图像边缘上或者是在图像平滑处;
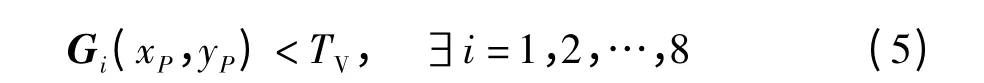
(2)如果P(xP,yP)在所有8 个微分响应矩阵中的值都大于设定阈值,则该点是一个候选的角点.
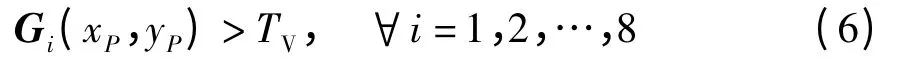
2 微分响应竞争抑制法
DLD 算法的优势在于去除边缘伪角点,但在大尺度缓变角点位置,它与其他角点检测算法一样,误检角点数明显增加,需要附加伪角点抑制步骤.图4(a)是火柴棒图像的格型微分角点检测的局部结果,在真实角点附近存在多个误检角点.由两条粗边缘相交而形成的两个顶点P1(3,3)和P2(5,3)如图4(b)所示,其8 微分响应值都大于阈值,即i=1,2,…,8,Gi(3,3)>TV和Gi(5,3)>TV.这种误检的原因是:①在格型分解中,一条图像边缘被划分为多条陪线,各陪线子集都映射了真实角点的几何结构,因此角点在多个子集中重复检出并不意外;②由于信号的连续性,在最优角点的小邻域内梯度值虽然单调减小,却不一定是跃变,造成真实角点附近同样具有大的梯度值,这是微分角点算法误检的共同原因.由于陪线分解具有同向同偏移的特点,同一结构的角点P1和P2需要合并.

图4 真实角点的重复检出Fig.4 Repeated detection of true corners
为减少误检角点,一般的检测算法直接把邻域尺寸作为阈值,合并该邻域内的所有角点[1],但这种做法在邻域内存在多个真实角点的情况下会造成漏检.文中提出一种更合理的微分响应竞争方案:①同一结构的角点,如图4(b)的P1和P2,它们隶属的陪线集相关,其格型微分响应值是相似的,通过竞争合并;②相异结构的角点,如P1和P3,它们的格型微分响应值存在着差异,需要保留.文中先定义角点相似度,该相似度用于判定两个角点是否为相同结构角点,然后给出竞争检测合并方法合并相似度大的角点.
2.1 角点相似度定义
根据上述同一结构的角点和相异结构的角点在格型微分响应上的差异性,对一个检出角点P 和它的重检角点Q,定义两个角点微分响应间的夹角余弦为相似度S(K,P):
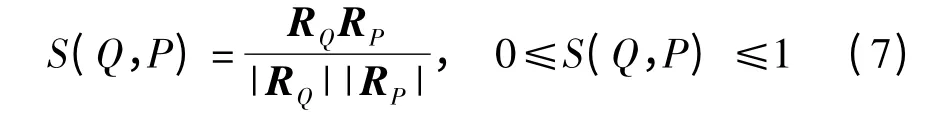
式中,RP是由微分响应矩阵幅值|Gi(xP,yP)|组成的8 维向量,

重检角点由阈值TS确定,如果相似度S(Q,P)比TS大,说明点Q 和点P 在微分响应矩阵中具有幅值相似的微分响应,则这两点是对同一真实角点的重复检出,采取竞争合并,反之则保留.TS∈[0,1],当TS=0 时,邻域响应竞争抑制法退化成根据邻域尺寸合并角点的一般算法;当TS=1 时,邻域响应竞争抑制法不起作用.根据平衡算法由得到的角点的误检率和漏检率选取阈值TS,下文3.2 节实验给出了TS经验值.
2.2 角点竞争合并检测算法
在角点竞争合并中,文中使用“胜者全取”(WTA)算法[14-15].该算法是竞争学习算法,规则为最近邻角点获胜,合并竞争获胜后的两个角点;其合并效果仅受角点距离所限.它用于角点合并时需要先确定最终检出角点数,但信号角点数待测.文中提出新的竞争规则,即先判断邻域尺寸阈值,然后在竞争过程中将获胜角点作为新角点,失利角点作为重检角点,对重检角点进行相似度判断并合并.文中提出的竞争抑制算法的步骤如下.
(1)初始化:设集合V 是DLD 已检出的候选角点集,从其第一个数据P1开始,建立P1的真实角点C1,设定邻域半径m.
(2)竞争合并阶段:选取第j 个数据Pj(j =2,3,…),假定此时已有L 个最终确定的真实角点,其位置分别为Cl(l=1,2,…,L).假设μq(q=1,2,…,L)为输出节点,则有

(3)更新:对第j 个数据Pj更新角点Cl'的位置:
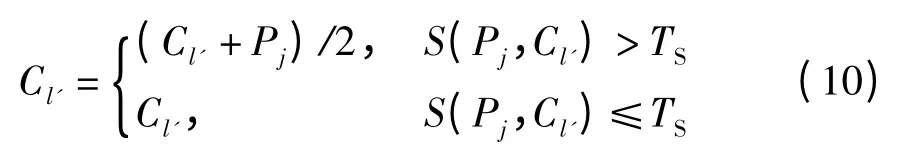
另外,更新候选检点集V=V-{Pj}.
(4)终止条件:V=∅时,角点合并结束.
邻域响应竞争抑制法不再简单地将在小邻域内检测到的角点进行合并,而是根据微分响应值分布对同一真实角点产生的误检角点进行合并,因而有效地避免了将小邻域内出现多个真实角点合并的情况.竞争抑制法的效果会受到竞争距离和相似度阈值TS的影响,TS越大抑制误检角点的能力越弱,反之抑制误检角点能力越强.
3 实验结果与分析
为评估DLD 算法的有效性,从3 个方面进行验证:①格型微分对边缘伪角点的抑制能力;②相似度阈值TS的选择;③不同角点检测算法的性能比较.实验结果采用误检率Re和漏检率Rm来衡量各算法检测角点的精确度,并采用ACU 函数比较误检率和漏检率的均衡程度.ACU 为查准率Na/No和查全率Na/Ng的加权和,ACU 值越大,则说明检测算法的性能越好.具体的错检率和ACU 函数的定义如下[16]:

式中,No为检出角点数,Na为检出角点中的真实角点数(正检角点数),Ng为真实角点数.
实验采用了6 幅测试图像,见图5.图5(a)-(c)为单个目标图像,图5(d)-(f)为多个目标图像,用于提供不同结构邻域角点竞争合并的对比数据.现有角点检测算法容易在图像边缘及背景点状纹理造成误检,其中,图5(b)叶子、图5(c)窗框和屋檐、图5(e)积木棱线、图5(f)火柴棒的边缘,用于检验去除边缘伪角点能力;图5(a)、(d)、(f)具有点状纹理,用于检验缓变角点的准确定位和伪角点抑制能力.真实角点由5 名熟悉角点检测任务,但不了解文中算法的测试者执行标定,如果4 个或以上的测试者在同一3 ×3 像素块内有标定点,则在其坐标平均值处标定一个真实角点.
在DLD 算法中,8 方向的微分把边缘划分到5条陪线上,方案中包含斜率为±2,故文中设置邻域尺寸为11 ×11.

图5 测试图像Fig.5 Test images
3.1 格型微分对伪角点的抑制能力

图6 边缘点的抑制效果Fig.6 Suppression effect of edge points
本实验对采用阶梯状微分方案的经典Harris 算法[3]和采用格型分解微分方案的DLD 算法进行比较,以评估DLD 算法对伪角点的抑制能力.图6 示出了两种算法测试火柴棒图像的结果,两者的检出点数均为214,正检角点数、误检角点数、漏检角点数等结果如表1 所示.从图6(a)可看出,Harris 算法在火柴棒的边缘(图6(a)左上和右中的标记圈处)以及背景的点状纹理(图6(a)左下的标记圈内)上存在伪角点;从图6(b)可看出,未作同陪线角点合并的DLD 算法仅在真实角点附近存在伪角点,与文中第2 节分析一致.对比两种算法的结果可得:格型微分角点检测即使在真实角点附近容易产生误检角点,其对边缘点和纹理点的抑制能力也要明显优于常规微分.
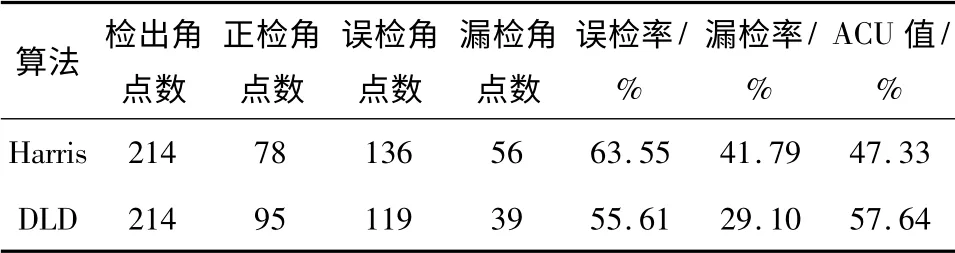
表1 Harris 和DLD 角点检测精度比较Table 1 Corner detection accuracy comparison between Harris and DLD
3.2 阈值TS的选取分析
DLD 算法中设计了两个阈值,其一是相似度阈值TS,其值会影响算法抑制重检角点的性能,不同图像的TS取值影响算法性能的效果较为接近.这是因为相似度由微分响应值决定,在不同图像中,相似角点微分值差异不大,因此相似度阈值TS在不同图像中的取值基本一致.另一个是微分阈值TV,其值会影响算法检出角点的数量,且不同图像受TV值的影响较大.为分析阈值对检出角点精确度的影响,首先对阈值TS进行测试,TS取大值会提高误检率,TS取小值会提高漏检率,根据实验结果选取一个合理TS值,该值应平衡误检率和漏检率,则图像的角点检测结果只由微分阈值TV确定.图7 是阈值TS的测试结果,TS取值范围为[0,1],步长设为0.05.其中图7(a)是固定微分阈值TV=50 时,测试6 幅测试图像得到的Re、Rm、ACU 平均值;图7(b)为4 个不同阈值TV下得到的ACU 平均值.
由图7(a)可得出以下结论:①当TS=1 时,即邻域响应抑制法不起作用,此时角点检测的误检率较大,漏检率较小,这是由于格型微分排除边缘误检点,致使对某一真实角点产生重复检出;②当TS=0时,即邻域响应抑制法退化成根据邻域尺寸合并角点的一般算法,合并效果与GLCP 算法[1]相同,此时误检率较小,但漏检率最大,这是由于仅根据邻域尺寸进行角点合并会将该邻域内的多个真实角点合并原始GLCP 和FAST 算法的结果受其阈值的影响,分别采用5 个不同阈值进行测试,取其误检率、漏检率、ACU 的平均值以体现实验结果比较的公平性.DLD 算法经测试发现其最优阈值TV处于[41,60]内,因此实验中DLD 算法将取TV=41,42,43,…,60共20 个值进行测试,然后取误检率、漏检率、ACU的平均值.图8 为各算法的误检率、漏检率和ACU成一个角点;③TS从0 至1 变化时,邻域内合并的角点数逐渐减少,误检率逐渐上升,而漏检率逐渐下降.

图7 阈值TS的选取Fig.7 Choice of TS
由图7(b)可见,当TS∈[0,0.6]时,ACU 值变化均比较平缓,此时误检率的上升与漏检率的下降处于平衡状态.这是由于随着相似度阈值TS增大,邻域内的多个真实角点得以保留,漏检率下降;此外,阈值的增大将使重检角点抑制效果减弱,误检率上升.当TS>0.6 时,ACU 曲线明显下降,此时误检率成为主导因素.这是由于格型分解致使多条陪线都反映出同一真实角点,导致DLD 算法重复检出角点,误检率上升趋势更为明显.因此,为平衡误检率和漏检率,文中取TS=0.6 用于后续算法性能对比实验.
3.3 不同角点检测器联合DLD 的改进性能比较
3.3.1 联合算法的总体性能比较
实验中与目前推荐的基于曲率的GLCP 检测器[1]和基于决策树的FAST 检测器[10]两种算法进行比较,GLCP 和FAST 均会在图像边缘或平滑区域产生一定的误检角点,DLD 算法能对这些误检角点进行抑制,本节实验将对以下4 种算法进行比较:原始GLCP 算法、引入DLD 的GLCP 联合算法、原始FAST 算法和引入DLD 的FAST 联合算法.值的比较结果,表2 是所有实验图像求得的总平均值结果.由图8 可得出以下结论:

图8 不同算法的精确度比较Fig.8 Accuracy comparison of different algorithms
(1)联合算法的角点检测误检率比原始算法有大幅度的降低,但漏检率有一定的提高,综合评价ACU 值表明联合算法的总体性能优于原始算法.

表2 不同算法的平均精确度比较Table 2 Comparison of average accuracy of different algorithms
(2)从图8(c)的综合评价ACU 值可发现,图5(a)、(d)得到的结果要优于其他图像,这是因为玩具车、战斗机图像的边缘特征明显,而且背景处存在大面积的点状纹理.对于这类具有明显边缘或具有点状纹理的图像,DLD 算法能充分体现其抑制边缘点和平滑区域点的优势,从而误检率降低.总体而言,GLCP+DLD 联合算法的ACU 值比GLCP 算法提高约8%~20%;FAST+DLD 联合算法的ACU 值比FAST 算法提高约5%~10%.
(3)对于图5(b)叶子的叶脉顶点、图5(c)房子的窗户顶点和图5(e)积木的棱线顶点,这些角点与邻近纹理区域的灰度相近,在角点处的DLD 微分响应值较小,而DLD 算法采用全局阈值TV,难以适应局部小变化,造成漏检率增大.总体而言,GLCP +DLD 联合算法的ACU 值比GLCP 算法提高8%~12%;FAST+DLD 联合算法的ACU 值比FAST 算法提高3%~10%.
从表2 可以看出,对于GLCP 检测器,引入DLD算法使误检率降低达34.59%,漏检率提高10.31%,且ACU 值提高12.14%;对于FAST 检测器,这3 个值分别为23.69%、11.05%、6.32%.
3.3.2 联合算法对边缘点的抑制效果
为更好地说明联合DLD 算法的抑制边缘点效果,本节对4 种算法的角点测试结果进行分析,如图9所示.GLCP 算法的阈值T1和T2,以及FAST 算法的阈值T 通过训练获得,选择准则为:检出角点数No和真实角点数Ng满足No≈1.5Ng;调整DLD 算法的阈值TV,使检出边缘点数约为检出角点数No的5%.其中GLCP 算法中的两个阈值分别设置为T1=0.17,T2=0.1,GLCP+DLD 联合算法在该基础上增加DLD 算法微分阈值TV=53;FAST 算法中的阈值设置为T=27,FAST +DLD 联合算法在该基础上增加阈值TV=42.4 种算法的检出角点数、正检角点数、误检角点数、漏检角点数见表3.

图9 不同算法的检测结果Fig.9 Detection results of different algorithms

表3 图9 各结果的精确度数据Table 3 Accuracy data of Fig.9
由图9(a)可见,GLCP 算法的误检主要在背景的点状纹理区域以及玩具车正面的线条上,其检出边缘点有27 个,占检出角点数的21.43%.经过DLD 算法的抑制后,误检角点大部分已被移除,如图9(b),检出边缘点仅2 个,占检出角点数的3.77%,其综合评价指标ACU 值从48.61%提高至64.62%.
由图9(c)可见,FAST 算法的误检主要在图像边缘上,如积木棱线,该算法检出边缘点有22 个,占检出角点数的12.02%.引入DLD 算法后,误检角点数从83 降至17,其中边缘点有6 个,占检出角点数的5.56%.另一方面,FAST 算法没有对邻近的检出角点进行合并,在角点的邻域内存在着重复检出的角点.DLD 算法采用邻域响应竞争法对重检角点进行合并,在积木顶点附近不存在多个检出角点,如图9(d),相应的ACU 值从68.99%提高至80.05%.
4 结论
文中定义了基于Directionlet 分解任意有理方向格型微分运算.基于该算子,文中提出了多向格型微分角点定位(DLD)方法,其能有效去除图像边缘伪角点和平滑区域伪角点.另外,针对真实角点重复检出问题,文中提出使用邻域响应竞争法对重检角点进行合并.实验证明,联合DLD 算法的GLCP 检测器的ACU 值可比原始GLCP 检测器提高12.14%;而联合DLD 算法的FAST 检测器的ACU 值可比原始FAST 检测器提高6.32%.
[1]He X C,Yung N H C.Corner detector based on global and local curvature properties [J].Optical Engineering,2008,47(5):057008/1-12.
[2]Kim S.Robust corner detection by image-based direct curvature field estimation for mobile robot navigation[J].International Journal of Advanced Robotic Systems,2012,9:1-12.
[3]Harris C,Stephens M.A combined corner and edge detector[C]∥Proceedings of the 4th Alvey Vision Conference.Manchester:University of Manchester,1988:147-151.
[4]Noble J A.Finding corners[J].Image and Vision Computing,1988,6(2):121-128.
[5]马丽红,任淼,谭幸均.基于局部熵和方差调整的Noble 角点检测算法改进[J].华南理工大学学报:自然科学版,2011,39(2):51-59.Ma Li-hong,Ren Miao,Tan Xing-jun.Modified Noble corner detection algorithm based on fine tuning of local entropy and variance[J].Journal of South China University of Technology:Natural Science Edition,2011,39(2):51-59.
[6]Ma L H,Tan X J,Tian J.An iterative strategy to approach corners using a new saliency measurement [C]∥Proceedings of IEEE International Conference on Acoustics,Speech and Signal Processing.Prague:IEEE,2011:1021-1024.
[7]Jiang D G,Yi J K.Comparison and study of classic feature point detection algorithm[C]∥Proceedings of 2012 International Conference on Computer Science and Service System.Nanjing:IEEE,2012:2307-2309.
[8]He W,Deng X L.A modified SUSAN corner detection algorithm based on adaptive gradient threshold for remote sensing image [C]∥Proceedings of 2010 International Conference on Optoelectronics and Image Processing.Haikou:IEEE,2010:40-43.
[9]Kumar R,Chen W C,Rockett P.Bayesian labelling of image corner features using a grey-level corner model with a bootstrapped modular neural network[C]∥Proceedings of Fifth International Conference on Artificial Neural Networks.Cambridge:IEE,1997:82-87.
[10]Rosten E,Porter R,Drummond T.Faster and better:a machine learning approach to corner detection [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(1):105-119.
[11]Kienzle W,Wichmann F A,Schölkopf B,et al.Learning an interest operator from human eye movements[C]∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE,2006:1-8.
[12]Velisavljevi'c V,Beferull-Lozano B,Vetterli M,et al.Directionlets:anisotropic multidirectional representation with separable filtering[J].IEEE Transactions on Image Processing,2006,15(7):1916-1933.
[13]Velisavljevi'c V,Vetterli M,Beferull-Lozano B,et al.Sparse image representation by directionlets [J].Advances in Imaging and Electron Physics,2010,161(C):147-209.
[14]张力明.人工神经网络的模型及其应用[M].上海:复旦大学出版社,1993:127-129.
[15]段敏,张锡恩.基于合并思想和竞争学习思想的聚类新算法[J].计算机工程与设计,2006,27(9):1656-1659.Duan Min,Zhang Xi-en.Novel clustering algorithm based on combination idea and competitive learning idea[J].Computer Engineering and Design,2006,27(9):1656-1659.
[16]Mokhtarian F,Mohanna F.Performance evaluation of corner detectors using consistency and accuracy measures[J].Computer Vision and Image Understanding,2006,102(1):81-94.
