传感器选择问题的GSS算法有效性分析与改进*

王小乐 黄宏斌 邓苏 刘明星

(国防科学技术大学 信息系统工程重点实验室，湖南 长沙 410073)

有限的节点能量和网络带宽制约着无线传感器网络(WSN)的性能.在观测物理系统时，节点所获的感知信息存在大量冗余，系统仅需选择部分节点的感知数据就能估计出系统状态.因此，采取合理的节点选择或调度策略，可以在保证估计精度的同时节约节点能量和网络带宽.文中研究了具有层次结构的WSN 节点选择问题(SSP:Sensor Selection Problem［1］or Sensor Scheduling Problem［2］).系统演化的不确定性和传感器观测过程的不确定性使SSP 的建模与求解变得非常复杂.SSP 研究如何从n 个传感器中选择m(1 ＜m ＜n)个传感器，使得融合中心根据这m 个传感器的观测数据估计出的目标系统状态最精确，该问题具有NP 难的复杂度［3］.例如:从n 个传感器中选择m 个传感器，总共有Cmn 种可能的组合，n 和m 较小时可以通过穷举搜索获得最优解，但是当两者较大时求最优解所花费的时间是目前的计算机无法承受的.例如，当n =100，m =25 时大约有1023种可能的解［1］，解空间呈指数增长.文献［4-5］采用贪婪策略提出了一种按顺序选择的算法即贪婪序列选择算法(GSS).从理论上讲GSS 并不能获得最优解，但文献［4］认为通过GSS 算法获得的解为最优解.

目前，求解SSP 的主要方法有:凸优化方法［1，6］、分支定界方法［7］、信息熵［2，8］、动态规划［9］、卡尔曼滤波［10］、粒子滤波［11］、随机场估计［12］等方法.Siddharth 等［1］给出了一种基于凸优化的启发式传感器选择算法，并给出了选择的最优传感器子集和最优性能上界，该算法并不能保证总能够获得与最优解差距较小的解，但是实验结果说明在大多数情况下所获得的解均与最优解差距较小.Mo 等［6］假设传感器的通讯开销远大于感知开销，提出了一种多阶段传感器选择策略，即在多个时刻调度传感器使其卡尔曼滤波器的误差协方差矩阵最小，并采用松弛凸优化的方法进行求解.Maciej 等［13］研究了通过传感器观测数据估计分布式系统参数的问题，目标是使用最少的传感器节点获得最精确的估计，他对问题建立多目标优化模型，并通过基于分支定界的序列二次规划方法对模型进行了求解.Zhen等［8］研究了信息物理融合系统(CPS)最优观测问题，并通过Fisher 信息熵的方法对问题进行建模与求解.Andrey 等［14］考虑了物理过程的不确定性和传感器噪声干扰，采用博弈类型的Riccati 微分方程和动态规划方程对问题进行求解.文献［5］提出了一种分布式在线贪婪算法，以效用函数满足子模块性的报酬递减特性为前提，在模型未知的情况下，通过在线学习的方法优化目标函数.文献［4］研究了任意时间卡尔曼滤波器(AKF)中的度量选择问题，为了获得最佳状态估计，选择过程可以被建模为一个双积分器，该文假设GSS 算法所提供的选择为最优选择，但是该假设并未经过理论证明，在文中仅通过一个特例说明在原文实验中成立.传感器选择主要应用于目标跟踪［15-17］、最优覆盖［18］、信息物理融合系统的最优观测［8，19］等问题中.传感器选择问题的最新研究包括可移动传感器的路径规划［7，20］、带天线的有向传感器网络中面向目标跟踪的传感器调度［21］等.

文中研究了GSS 算法在求解SSP 上的有效性，通过反例证明该算法并不保证获得最优解.通过理论分析了初始解对GSS 算法性能的影响，提出了选择更加有效的初始解的GSS 改进方法，通过仿真实验验证GSS 改进算法的有效性.并以目标跟踪问题为实例进行仿真实验.

1 模型与问题描述

1.1 观测模型

将被观测系统称为目标系统，假设传感器网络中包含n 个传感器，用集合S ={s1，s2，…，sn}表示.假设单个传感器的观测模型描述为

yi=HiX+vi，i=1，2，…，n.

式中:yi为传感器i(i=1，2，…n)，的测量值，可能是数值，也可能是列向量;vi∈Rl(i =1，2，…n)，为第i传感器的高斯白噪声干扰，其均值为零，协方差矩阵为Σi，即vi～N(0，Σi);X 表示目标系统的状态，X∈Rd;l 为观测向量的维度，Hi(i=1，2，…n)为l×d 维观测矩阵.如果观测模型是非线性模型，可以通过泰勒展开的方法将其近似为线性模型.

1.2 状态估计与评价

状态估计就是在目标状态X 未知的情况下，如何通过观测数据Y=(y1，y2，…，yn)T和观测矩阵Hi(i=1，2，…，n)构造系统状态X 的最优估计函数(Y)(简写为).文中假设融合中心对系统状态X并无先验知识，采用最小二乘估计，即通过对残差函数G 求导，令其导数矩阵为零，在解线性方程组便可获得估计函数，过程如下:

估计误差的协方差为

1.3 传感器选择问题

根据1.2 中分析，可将传感器选择问题描述为

由传感器选择问题的模型可知，进行传感器选择的依据是每个传感器的观测矩阵和噪声的协方差矩阵，根据不同的选择计算出目标函数J(z)，使其最大的选择为最优选择.从问题P0可以看出，SSP 为一个组合优化问题，除了穷举搜索算法，通过其他优化算法均不能保证获得最优解.因此，可通过启发式方法寻求一种尽可能好的次优解.

2 GSS 算法分析及改进

2.1 GSS 算法基本思想

GSS 算法是所选传感器个数逐次递增的方法，每次迭代增选一个传感器，使本次迭代增加的传感器与已选传感器构成的子集的标函数最大，通过依次迭代直到选够m 个传感器就可以获得传感器选择的一个解.GSS 算法如下所示:

给定被选择集合S ={s1，s2，…，sn}，初始选择集S'0=，已知m.

文献［4］提出了一个假设，认为通过GSS 算法能够获得最优解，但并没有给出理论证明，该假设是否成立以及这种算法到底是否有效，现有文献并未肯定或否定.文中将通过理论和实验两个方面说明GSS 算法并非保证能获得最优解，但是一种有效的传感器选择算法.

GSS 算法从选择一个传感器开始每次迭代增选一个传感器直到选够m 个传感器，因此，从n 个传感器中选择m 个传感器的时间复杂度为

由式(4)可知，GSS 为线性时间复杂度，它与传感器总数n 呈线性关系.

2.2 GSS 最优性分析

定义1(最优k 子集):在传感器选择问题中，将选择k 个传感器的最优选择子集称为最优k 子集，其中n≥k≥1.

假设1 最优k 子集一定包含最优k-1 子集.

定理1 假设1 成立则GSS 算法为最优选择算法.

证明显然当第一步选择的是最优的子集，后面每次增加的都能保证最优，那么最终选择也一定为最优.

一般情况下，传感器观测噪声的统计特征相同，假设Σi=1 (i=1，2，…，n).

以式(5)为条件通过数学推导很难获得式(6)，但是可以通过举反例很容易证明假设1 不成立.假设d=2，l=1 时，找到如下一组传感器观测向量数据H，采用穷举搜索其最优选择子集，获得的选择结果见表1，H 中第i(1≤i≤10)列表示传感器i 的观测矩阵Hi，

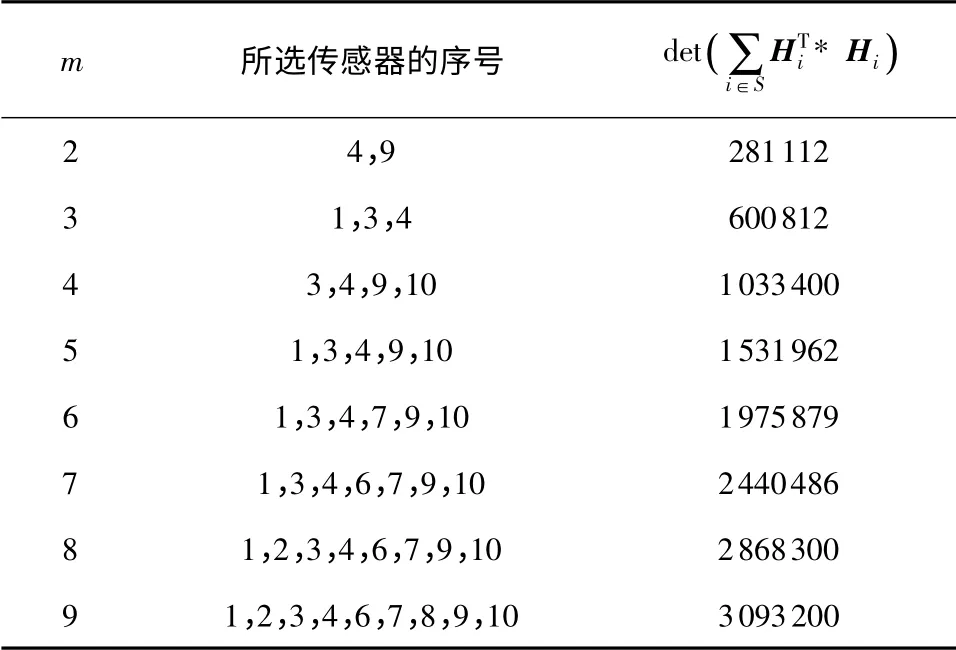
表1 观测矩阵为H 的传感器选择结果Table 1 Sensor selection results of observation matrix H

从表1 中的选择结果可以看出:最优3 子集中不含9，最优2 子集与最优3 子集之间的关系违反了假设1，因此假设1 是不成立的.如果在最优3 子集中选择了传感器4 和9，那么所获得的3 子集就不是最优3 子集1、3、4，从而可以看出GSS 算法并不保证所获得的传感器是最佳选择.

2.3 GSS 算法改进

GSS 算法的起点是从选择1 个传感器开始的，这对于目标系统状态是数值(d =1)的情况是成立的.但是，如果系统状态是向量，并且其维度d≥l时，选择1 个传感器根本无法估计出系统的状态，更谈不上减小误差了，此时目标函数J 为负无穷大，那么就无法比较选择哪个传感器更好，因此导致GSS算法的起点等同于随机选择.

南方丘陵区旱地水稻种植自然水资源微循环灌溉系统试验研究…………………………………………………… 汪跃宏(17.57)

定理2 当传感器观测值为数值(即l=1)时，对于任意一个传感器选择子集S'，当|S'| ＜d 时，对于任何感知矩阵Hi(i=1，2，…，n)都有

证明 定理2 可以理解为当变量个数大于方程个数时，方程有无穷多解.

对于观测为向量的情况(即l ＞1)时，可以将每个传感器认为是由l 个子传感器构成，其中每个子传感器只有1 个观测值.在进行传感器选择时，增加约束条件:这些子传感器要么同时被选择，要么都不选.此时，容易获得推论1.

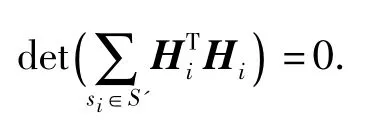
给定被选择集合S ={s1，s2，…，sn}，初始选择集S'0=，已知m.

此处k 较小，一般时间复杂度约为O(nk)，一般情况下k≤4.

3 仿真结果分析

3.1 GSS 改进算法的有效性实验

前文中虽然通过反例证明了GSS 算法并不保证获得最优选择，但在实际中仍是一种高效的算法.假设观测值是数值，目标系统状态向量为2 维向量.

(1)随机产生观测向量，对n = {5，6，7，8，9，10}，m={3，4，…，n-1}通过matlab 进行交叉仿真测试.此处之所以如此设置，是因为测试中需要用穷举搜索计算最优选择以便对比，如果参数n 较大会导致仿真时间过长.进行每组参数设置，进行1 000次蒙特卡洛仿真，根据定理1 只要违反假设1 就不能用GSS 获得最优解，否则就一定能获得最优解.因此，计算违反假设1 的次数，实验结果如图1所示.

图1 GSS 改进算法有效性测试Fig.1 Validity test of improved GSS algorithm

从图1 可以看出，随着选择个数的增加，违反次数递减，随着传感器总数的增加违反次数增大，但是1000 次实验中最多违反次数为80 次，也就是有920次都符合假设1，这说明GSS 改进算法在大多数情况下都能获得最优选择.

(2)如果违反假设，GSS 改进算法所获得的传感器选的目标函数值与最优选择的目标函数值之间的差反应了GSS 算法所获近似解的近似程度.假设在n = {9，10，11，12，13，14，15}的情况下分别对m={3，4，5，6，7，8}几组数据各进行1 000 次测试，计算目标函数J 与最优选择目标函数的误差百分比，结果如图2 所示.目标函数之差的百分比Q 计算由式(7)得到:

式中:J'i表示第i 次蒙特卡洛仿真GSS 改进算法所获得的目标函数，表示第i 次蒙特卡洛仿真的最优目标函数.

图2 GSS 改进算法最优性测试结果Fig.2 Optimal test results of improved GSS algorithm

从图2 可以看出，GSS 改进算法与最优算法的目标函数之差的百分比小于0.35%，而且随着选择数目的增加GSS 获得的解更接近于最优解，当选择数大于5 时误差小于0.05%，可见GSS 改进算法非常近似于最优解.从图2 中也可以看出传感器总数变化对GSS 改进算法的最优性影响并不大.

3.2 GSS 与其改进算法的对比

传感器选择常用于目标跟踪问题中.在本实验中，假设平面上随机均匀部署了多个传感器节点.目标是匀速直线运动(CV 模型)，其系统可以描述为Xk+1=FXk+wk.其中:Xk=(px，vx，py，vy)T，p、v 分别为目标的位置和速度;wk为随机干扰;F 为目标系统状态转移矩阵，在CV 模型中，

式中:ΔT 表示离散化运动模型后的时间片长度;wk为环境噪声干扰，为高斯白噪声，其均值为零，协方差矩阵为R.

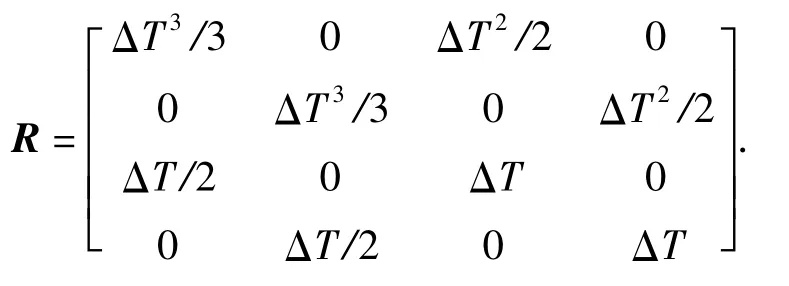
该实验采用的传感器模型为DoA 模型，DoA 模型的传感器观测量是目标到传感器的方位角，如式(8)所示:

设置传感器总数n 为50，每个时刻选择6 个传感器，目标从(0，0)点开始以速度(10 m/s，12 m/s)匀速运动，传感器抽样频率为1 s，系统仿真为50 s，对GSS 算法、GSS 改进算法和距离最近优先选择算法这3 种算法进行传感器选择实验，将选择的目标函数、位置估计误差的均方根(RMSE)进行对比，如图3 所示.图中的最小参考误差是指不进行选择而将所有传感器都激活得到的估计误差，这是系统能达到的最小误差.

图3 目标跟踪误差对比Fig.3 Comparison of target tracking error

从图3 中误差对比可以看出，总体误差基本在1 m 左右，相对目标运动速度根据所选择的传感器估计出的目标位置比较精确，改进GSS 算法比原始算法精度要高.图3 中两边的误差较大，原因是:在目标跟踪问题中，传感器部署在平面区域上，而目标轨迹的前端和后端由于传感器部署密度相对较小且并没有环绕目标，因此造成这种情况的出现.这也恰好说明了案例的合理性.

根据文献［13］可知，观测模型越灵敏所提供的信息量越大，因此，基于距离的传感器选择算法也是有效的，但是SSP 不仅仅看单个传感器灵敏性，还考虑所选传感器之间的组合效应，基于距离的方法在这方面没有考虑，因此较文中所研究的两种方法稍差.

对所选传感器个数m 对估计精度的影响进行了实验分析，设置传感器总数n =100，所选传感器个数m 从2 增加到22，分别进行100 次仿真，计算估计误差的平均值，结果如图4 所示.

图4 选择个数与估计精度的关系Fig.4 Relationship between selection number and evaluation precision

由图4 可以看出，当传感器较少时，增加传感器个数对降低误差的贡献非常大，这也就是SSP 问题的子模块性［22］.从图中还可以看出，存在一个较好的传感器数ħ=6，当选择传感器数大于ħ 时，再增加传感器数对估计误差减少的影响并不明显，称之为Carathéodory 界限［6］，该界限的存在恰好说明了进行传感器选择的意义.

4 结语

SSP 是具有NP 难复杂度的多维组合优化问题，通过分步决策进行选择的GSS 算法是求解SSP 的有效方法.文中对GSS 算法进行分析研究，通过反例证明了GSS 算法不保证得到最优解.GSS 算法的第一步选择影响着算法的最优性，通过分析笔者认为如果第一步能够采用穷举搜索获得最优的初始传感器选择，就能提高算法的最优性.在此基础上提出了一种GSS 的改进算法，GSS 改进算法仍为多项式时间复杂度.GSS 改进算法在大多数情况下能够获得最优解;即便不能获得最优解，所获得的次优解也非常接近于最优解;这证明了GSS 改进算法的有效性.最后将文中算法应用于目标跟踪应用实例，实验表明，GSS 改进算法较原算法获得的选择子集估计精度更高.

［1］Siddharth Joshi，Stephen Boyd.Sensor selection via convex optimization［J］.IEEE Transactions on Signal Processing，2009，57(2):451-462.

［2］Miao Lifeng，Stefanos Michael，Narayan Kovvali，et al.Multi-source neural activity estimation and sensor scheduling:algorithms and hardware implementation［J］.Journal of Signal Processing Systems，2013，70(2):145-162.

［3］Yoo Tae-Sic，St phane Lafortune.NP-Completeness of sensor selection problems arising in partially observed discrete-event systems［J］.IEEE Transactions on Automatic Control，2002，47(9):1495-1499.

［4］Nima Moshtagh，Chen Lingji，Raman Mehra.Optimal measurement selection for any-time Kalman filtering with processing constraints［C］∥John Ballieul，Gao Lei.Proceedings of the Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference.Shanghai:IEEE，2009:5074-5081.

［5］Manohar Shamaiah，Siddhartha Banerjee，Haris Vikalo.Greedy Sensor selection under channel uncertainty［J］.IEEE Wireless Communications Letters，2012，1(4):376-379.

［6］Mo Yilin，Ambrosino Roberto，Sinopoli Bruno.A convex optimization approach of multi-step sensor selection under correlated noise ［C］∥Vincent Conitzer.Proceedings of Forty-Seventh Annual Allerton Conference Allerton House.Champaign:IEEE，2009:187-193.

［7］Christophe Tricaud.Optimal sensing and actuation policies for networked mobile agents in a class of cyber-physical systems［D］.Logan:ECE Department，Utah State University，2010:45-52.

［8］Zhen S，Chen Y Q，Chellury R S，et al.Optimal observation for cyber-physical systems［M］.New York:Springer，2009:14-25.

［9］Li Y，Krakow L W，Chong E K P，et al.Approximate sto-chastic dynamic programming for sensor scheduling to track multiple targets ［J］.Digital Signal Processing，2009，19(6):978-989.

［10］Xiao W D，Wu J K，Xie L H，et al.Sensor scheduling for target tracking in networks of active sensors［J］.Acta Automatica Sinica，2006，32(6):922-928.

［11］Muhammad Naeem，Udit Pareek，Daniel C Lee.Swarm intelligence for sensor selection problems ［J］.IEEE Sensors Journal，2012，12(8):2577-2584.

［12］Weng Y，Xie L H，Xiao W.Sensor selection for random field estimation in wireless sensor networks［J］.Journal of System Science and Complex，2012，25(1):46-59.

［13］Maciej Patan，Dariusz Uciński.Resource-aware sensor activity scheduling for parameter estimation of distributed systems［C］∥George A Bekey，George N Saridis.Proceedings of the 18th IFAC World Congress.Milano:International Federation of Automatic Control (IFAC)，2011:9984-9989.

［14］Andrey V Savkin，Robin J Evans，Efstratios Skafidas.The problem of optimal robust sensor scheduling ［J］.Systems ＆ Control Letters，2001，43(2):149-157.

［15］Zoghi M，Kahaei M H.Adaptive sensor selection in wireless sensor networks for target tracking［J］.IET Signal Process，2010，4(5):530-536.

［16］Tharmarasa R，Kirubarajan T，Sinha A，et al.Decentralized sensor selection for large-scale multisensor-multitarget tracking［J］.IEEE Transactions on Areospace and Electronic Systems，2011，47(2):1307-1324.

［17］Chen Y C，Wen C Y.Decentralized cooperative TOA/AOA target tracking for hierarchical wireless sensor networks［J］.Sensors，2012，12(5):15308-15337.

［18］Gil J M，Han Y H.A target coverage scheduling scheme based on genetic algorithms in directional sensor networks［J］.Sensors，2011，11(2):1888-1906.

［19］Zhen S，Chellury R S，Nazif Cihan Tas，et al.Feasibility analysis on optimal sensor selection in cyber-physical systems［C］∥Chiasson John，Karlene A Hoo.Proceedings of 2009 American Control Conference.Hyatt Regency Riverfront.St.Louis:AACC，2009:5368-5373.

［20］Xing G L，Wang J P，Yuan Z H，et al.Mobile scheduling for spatiotemporal detection in wireless sensor networks［J］.IEEE Transactions on Parallel and Distributed Systems，2010，21(12):1851-1866.

［21］Cai Y L，Lou W，Li M L，et al.Target-oriented scheduling in directional sensor networks［C］∥Robert L Baldwin，Qiao Chunming.Proceedings of IEEE INFOCOM 2007.Anchorage:IEEE，2007:1550-1558.

［22］Andreas Krause.Optimizing sensing［D］.Pittsburgh:School of Computer Science，Carnegie Mellon University，2008:3-15.