基于自适应反步法的自主水下机器人变深控制*

贾鹤鸣 宋文龙† 陈子印

(1.东北林业大学 机电工程学院，黑龙江 哈尔滨 150040;2.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

随着自主水下机器人(AUV)在海洋工程领域的不断应用，通常将AUV 的控制器设计分为3类，即对纵向速度、水平面航向/航迹和深度控制3 个解耦的子系统分别设计控制器［1］.其中AUV 深度控制在海底地形跟踪与测绘、石油管道检测、沉船探测作业中具有重要作用.考虑到海洋环境的复杂多变性和海洋运动体总会受到海流干扰的影响［2］，工程上要求AUV 的深度控制器具有对模型中非线性水动力参数变化的鲁棒性和对外界海流干扰作用的适应性［3］，以满足不同工况下的海底作业需求.

目前，国内外对AUV 的变深控制器的设计大多采用基于线性化模型的方法［4-6］，假设模型在工作点小范围邻域内是稳定的，然后根据不同的工作点对模型进行线性化处理，设计一系列的控制器和切换规则实现对不同工况下AUV 的变深控制;由于未考虑模型中的非线性项和未建模动态的存在，因此无法保证系统的全局渐近稳定.考虑到AUV 模型中的非线性水动力阻尼系数无法精确已知和外界海流干扰作用的存在，文献［7］中提出基于专家知识和模糊函数的扩展自适应模糊滑模深度控制器，其对参数变化和扰动具有一定的鲁棒性.文献［8］中利用模糊神经网络对滑模控制器的增益进行在线调整，保证了系统的鲁棒性，但由于采用梯度法设计自适应规律，无法保证参数收敛速度和系统的全局稳定性.为了实现对模型中的不确定性进行在线估计和补偿，文献［9］中提出构建一种基于S 函数的过程神经元模型控制器，其对非线性参数变化具有一定的鲁棒性，但采用梯度法设计参数学习算法无法保证Lyapunov 稳定意义下的全局收敛性.Li 等［10-11］提出了基于神经网络的自适应深度控制方法，利用神经网络对非线性函数的逼近特性能够对有界扰动和未建模动态进行在线补偿;Zhang 等［12］给出了基于DRFNN 的AUV 运动控制器，与传统神经网络相比，DRFNN 具有更快的收敛速度，并通过DRFNN 对垂直方向上的动态非线性项进行补偿学习，从而实现了AUV 对垂直面曲线的精确跟踪.但文献［10-12］均未考虑存在攻角下的控制器形式，即未充分考虑AUV 模型中的非线性特性.

文中基于反步法迭代设计AUV 变深控制器，针对AUV 模型的运动学和动力学部分分别迭代设计控制器，设计过程中考虑了模型中存在合速度与纵倾角方向不一致时的攻角问题，更加精确地反映AUV 的非线性动力学特性;同时，通过引入神经网络对纵倾运动中的不确定性进行在线辨识，并基于Lyapunov 稳定性理论设计神经网络权重的学习律，以保证存在估计误差时闭环系统的一致最终有界.

1 AUV 垂直面运动模型

忽略横摇运动对垂直面运动的影响，得到简化的垂直面运动方程［3］，并假设AUV 的纵向速度u 由推力系统单独控制保持在稳定航速ud.

运动学方程为［13］

式中:z 为AUV 的下潜深度;攻角α=tan-1(w/u)，w为AUV 的垂向速度;vt为AUV 的合速度，定义为;θw为AUV 升沉运动过程中的潜浮角，θw=θ+α，θ 为AUV 的纵倾角;q 为AUV 的纵倾角速度.

动力学方程为［13］

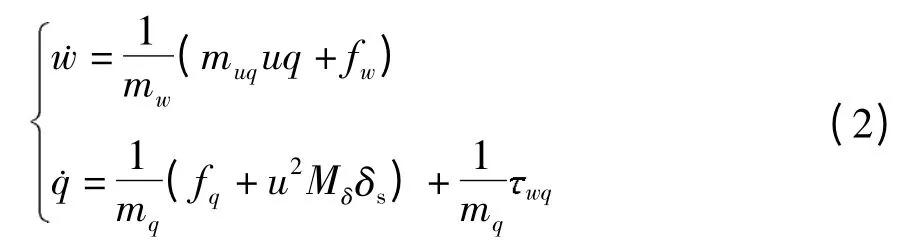
其中，

式中:m、m(·)分别为AUV 的质量和附加质量;Iy为AUV 绕y 轴的转动惯量;Z(·)、M(·)均为非线性水动力阻尼系数;zg为载体坐标系下垂直轴上的重心位置;W 和B 分别表示AUV 受到的重力和浮力;控制输入δs为AUV 的升沉舵角;wq为AUV 的模型不确定项和外界海流干扰.

2 控制器设计

欠驱动AUV 变深控制器的设计目的是根据运动学方程(1)和动力学方程(2)，在保持纵向速度ud＞0 恒定下，对于给定的阶跃深度参考信号zd，设计反馈控制规律和自适应律，使得实际下潜深度z跟踪期望深度zd，即满足其中t 为响应时间，ze为深度跟踪误差.

定义坐标变换如下:

式中，β1和β2分别定义为AUV 的潜浮角和纵倾角速度的虚拟控制量来实现相应子系统的静态补偿，θe为纵倾角误差，qe为纵倾角速度误差.假设AUV速度是非负的，即不能倒车航行，则AUV 在潜浮运动时满足θw∈(-/2，/2)成立.

下面结合反步法迭代构造Lyapunov 能量函数的思想设计虚拟控制量和AUV 变深控制器.

2.1 运动学控制器设计

第一步 结合式(1)、(4)可得

由于存在θw∈(-/2，/2)，使得0 ＜(sinθw)/θw≤1，则式(5)可以变形为

考虑Lyapunov 函数

对式(7)求导得

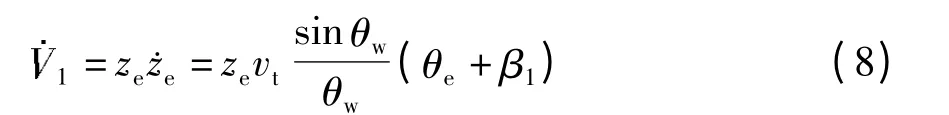
设计虚拟控制量β1=-c1ze，则式(8)整理得

第二步 结合式(7)，选取Lyapunov 函数为

式中，p1是一个正常数.

对式(10)两边求导，并将式(9)代入得

由式(1)、(4)得

代入式(11)得

选取虚拟控制量为

其中，c2＞0.

式(14)变为

需要说明的是，假定AUV 的最大纵向航速为umax，即所有时刻下都存在u≤umax，同时AUV 的垂向速度较小且存在由于vt=则有，即当选择合适的c2大于c1与vt上界的乘积时，可使得成立.

2.2 动力学控制器设计

实际工况下，AUV 在下潜运动时水动力阻尼系数会发生一定范围内的变化，产生AUV 的模型参数摄动，致使出现模型不确定项，这会给控制器设计带来一定困难，再加上AUV 会受到外界海流干扰从而影响控制效果，文中考虑神经网络具有非线性映射和在线学习的特点，采用径向基神经网络(RBF)对模型中的不确定和干扰项进行逼近

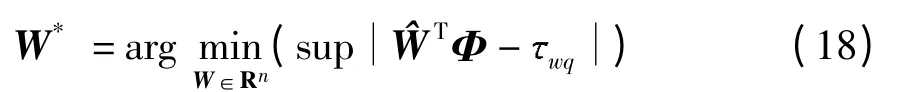
式中:aj为隐含层第j 个基函数的中心;σj为基函数的宽度.

因此，式(2)可以表示为

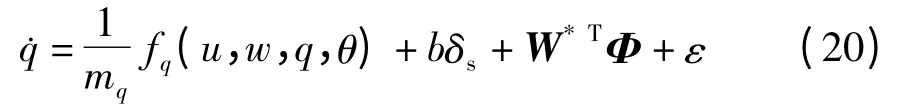
其中，b=u2Mδ/mq.

定理 考虑AUV 的动态模型(1)、(2)和跟踪误差方程(4)，如果设计控制规律为式(29)，神经网络权重的在线学习算法为式(30)，则能够保证闭环系统的所有信号及状态一致最终有界，且收敛到原点附近极小的邻域内.

证明 结合式(10)选取Lyapunov 函数为

设计AUV 动力学等价控制器为

由式(4)和(15)得

其中，

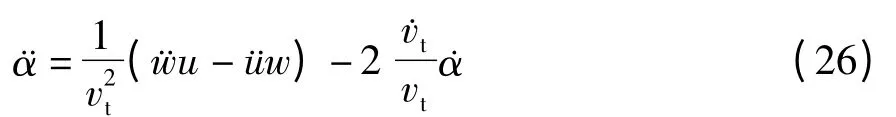
由动力学方程(2)，式(26)可变为

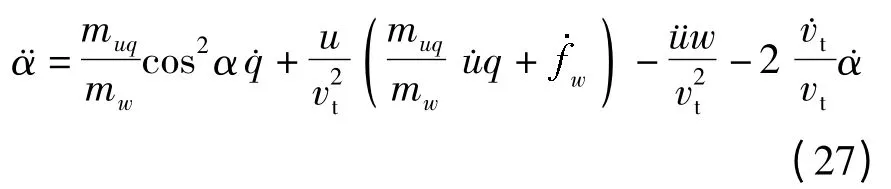
由于式(27)中含有攻角的二阶导数，因此存在状态变量q 的同类项，整理后得到

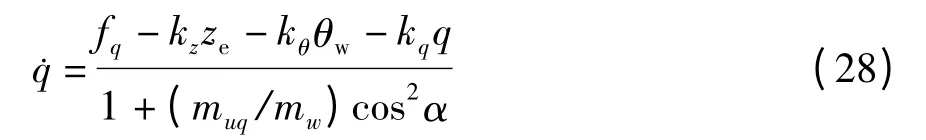
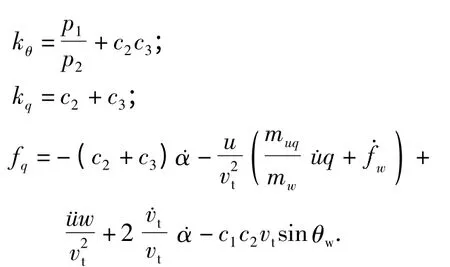
则控制输入和神经网络的自适应律可以选取为

式(23)变为

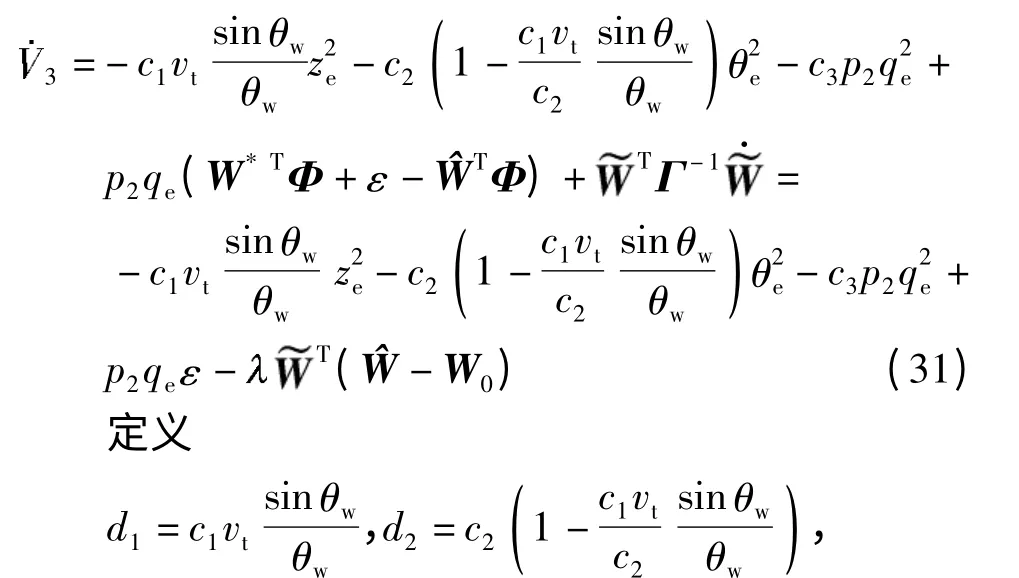
则式(31)变为

由Young’s 不等式［15］得

其中，γ 是一个正常数.进一步，

对不等式进行缩放得

由上式得

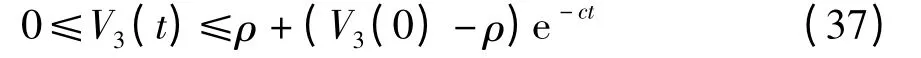
考虑式(36)和(37)，基于Lyapunov 稳定性理论，可知闭环系统的所有信号及状态一致最终有界［15］.

证毕.

3 仿真实验

为验证文中设计的控制器在参考深度变化时的跟踪效果，针对文献［3］中AUV 的数学模型，在相同的初始条件下利用PID 控制器对同一期望跟踪深度信号进行仿真，控制器增益参数选择为c1=0.08，c2=0.2，c3=20，p2=100，PID 控制器的增益参数选择为kP=30，kD=120.5，kI=0.05，期望速度ud=1 m/s，选取RBF 神经网络输入层为3 个节点，隐含层的神经元为12 个，输出层1 个节点，高斯基函数的中心点均匀地分布在［-0.5，0.5］的区间上，神经网络权值的初始值W0=0，σ =，增益参数=1.5，Γ=diag(10，10，…，10).设计两组实验，比较文中设计的控制器在设定控制器增益参数下的系统响应和在扰动作用下的变深控制性能.

实验1 为验证设计的控制器在深度变化时的跟踪效果，选取PID 控制器作为对比，初始条件为［z θ q w］=［0 0 0 0］，参考深度(单位:m)变化为

图1 为AUV 的变深控制响应和深度跟踪误差(ze)曲线.由图1 可以看出，文中设计的控制器能够适应不同的深度变化，实现无超调量的跟踪效果.图2为两种控制器作用下的AUV 各状态变量变化曲线和舵角δ 变化曲线.从图2 中可以看出，文中设计的控制器的舵角变化更为平缓，而PID 控制器的跟踪响应曲线具有一定的超调，导致控制舵角输出具有较大的峰值和出现陷入饱和区的现象.

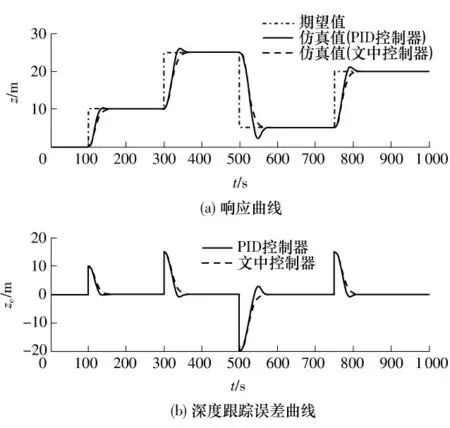
图1 变深控制响应和深度跟踪误差曲线Fig.1 Diving control response curves and tracking error curves

图2 各状态变量变化曲线Fig.2 Changing curves of states

实验2 为验证文中设计的控制器在扰动作用下的鲁棒性，采用与实验1 相同的PID 控制器参数与控制器增益参数时的变深控制效果进行对比.从超调量和调节时间的对比可以看出，传统的PID 控制器在固定工作点下的控制性能能够满足控制指标要求，但当AUV 受到环境干扰力作用或工作点发生变化时的控制效果较差.图3 为扰动作用下变深控制的响应和深度跟踪误差曲线，从图3 可以看出，在不改变控制器参数的前提下，PID 控制器无法实现对扰动作用的抑制，且无法实现变深控制，而文中提出的非线性控制器由于具有自适应机制，所以能够对扰动作用进行补偿，与PID 控制器相比具有较小的稳态误差，跟踪精度较高.图4 为AUV 各状态变量的变化曲线和控制舵角变化曲线.从图中可看出扰动作用下系统状态仍然变化平稳，AUV 可以获得稳定的控制效果.

图3 扰动作用下变深控制响应和深度跟踪误差曲线Fig.3 Diving control response curves and tracking error curves in the presence of disturbances

图4 扰动作用下各状态变量变化曲线Fig.4 States changing curves in the presence of disturbances

4 结语

文中针对水下机器人的变深控制问题，基于反步法和Lyapunov 稳定性理论，迭代设计了AUV 运动学控制器和动力学控制器，并通过设计神经网络控制器保证系统在存在模型参数不确定和外界海流扰动下的稳定性，最后通过数值仿真实验验证了文中提出的控制方法的有效性.由于未对海洋中真实的海流干扰进行建模，故无法模拟真实的海洋环境特性，下一步工作将详细研究真实海洋干扰对AUV 运动控制问题的影响，以期提出相应的控制方法.

［1］蒋薪松，封锡盛，王棣棠.水下机器人［M］.沈阳:辽宁科学技术出版社，2000:55-60.

［2］Bovio E，Cecchi D，Baralli F.Autonomous underwater vehicles for scientific and naval operations［J］.Annual Reviews in Control，2006，30(2):117-130.

［3］Silvestre C，Pascoal A.Depth control of the INFANTE AUV using gain-scheduled reduced order output feedback［J］.Control Engineering Practice，2007，15(1):883-895.

［4］Feng Z，Allen R.Reduced order H∞control of an autonomous underwater vehicle［J］.Control Engineering Practice，2004，12(12):1511-1520.

［5］刘旌扬，冯正平，易宏，等.水下机器人H∞控制系统设计［J］.海洋工程，2008，26(3):70-78.Liu Jing-yang，Feng Zheng-ping，Yi Hong，et al.Design of H∞control system for autonomous underwater vehicles［J］.The Ocean Engineering，2008，26(3):70-78.

［6］汪伟，边信黔，王大海.AUV 深度的模糊神经网络滑模控制［J］.机器人，2003，25(3):209-214.Wang Wei，Bian Xin-qian，Wang Da-hai.Fuzzy neural network sliding-mode control of auto depth for AUV［J］.Robot，2003，25(3):209-214.

［7］Kim H S，Shin Y K.Expanded adaptive fuzzy sliding mode controller using expert knowledge and fuzzy basis function expansion for UFV depth control ［J］.Ocean Engineering，2007，34(1):1080-1088.

［8］Lionel L.Robust diving control of an AUV ［J］.Ocean Engineering，2009，36(11):92-104.

［9］唐旭东，庞永杰，李晔.一种水下机器人运动的过程神经元控制［J］.控制理论与应用，2009，26(4):420-424.Tang Xu-dong，Pang Yong-jie，Li Ye.A process neural control algorithm for autonomous underwater vehicle［J］.Control Theory and Applications，2009，26(4):420-424.

［10］Li Ji-Hong，Lee P M.A neural network adaptive controller design for free-pitch-angle diving behavior of an autonomous underwater vehicle［J］.Robotics and Autonomous Systems，2005，52(2):132-147.

［11］Li Ji-Hong，Lee P M，Jun B H.A neural network adaptive controller for autonomous diving control of an autonomous underwater vehicle［J］.International Journal of Control，Automation，and Systems，2004，2(3):374-383.

［12］Zhang Li-jun，Qi Xue，Pang Yong-jie.Adaptive output feedback control based on DRFNN for AUV［J］.Ocean Engineering，2009，36(10):716-722.

［13］李殿璞.船舶运动与建模［M］.北京:国防工业出版社，2008:11-12.

［14］Polycarpou M.Stable adaptive neural control scheme for nonlinear systems［J］.IEEE Transactions on Automatic Control，1996，41(3):447-451.

［15］程代展.应用非线性控制［M］.北京:机械工业出版社，2006:82-86.