二阶多智能体系统的跟随者-多领导者聚集控制*

刘学良 胥布工

(华南理工大学 自动化科学与工程学院，广东 广州 510640)

近年来，多智能体系统或群体系统协调控制问题已成为控制界研究者关注的焦点.这主要是因为协调控制在多机器人编队控制［1-2］、群集运动［3］、一致性［4-5］、分布式传感器网络［6-7］、混沌系统的同步［8-9］等方面有着重要的应用.

聚集控制是多智能体系统协调控制中的基本问题之一，指的是空间分布的几个个体或者智能体通过邻居之间的局部信息交换，最终聚集于一个期望的目标区域内.在多智能体系统协调控制中，协调的目标可能是一个，也可能是多个，或者是多个目标组成的一个集合.聚集控制问题中存在多个(虚拟)领导者，这些领导者只能发送它们的状态信息给邻居跟随者，而跟随者不能将自己当前的状态信息反馈给领导者.在实际应用(如异类机器人避障、狼群对鹿群捕食、蚁群搬运食物等)中，领导者可能不会是一个简单的个体，而会是一个区域，故将这个目标区域模拟成多个领导者组成的集合.在聚集控制中，一个关键的问题是如何设计一个分布式控制协议使得一个多智能体系统聚集于一个期望的目标区域内.国内外学者已对群体系统的聚集控制进行了大量的研究.Hu 等［10］提出了一阶连续时间线性多智能体系统的静态聚集控制模型;Li 等［11］研究了有向连接通信拓扑下高阶智能体系统的包容控制问题，分别讨论了连续时间和离散时间两种情形，并基于邻居相对输出状态构造了一个新的降阶控制协议，给出了降阶控制协议的设计方法;文献［12］和［13］分别基于外心算法和人工热能函数方法给出了能保持网络的连通性的聚集控制算法;此外，Shi 等［14］分析了智能体动态是非线性和网络通信拓扑是时变情形下的聚集控制问题.但是，对于二阶多智能体系统和网络存在通信时延、噪声等不确定性的聚集控制问题则很少涉及.

对于实际的多智能体网络，因为网络时延、通信噪声、丢包、带宽受限等诸多不确定性的存在，致使智能体之间不能获得准确的邻居状态信息，并可能导致整个多智能体系统不稳定甚至实现不了期望的群体行为模式;另一方面，一些实际系统(如无人驾驶飞机、水下机器人等)都是通过它的加速度而非速度来调整它的运动，使得研究具有二阶或者更高阶的多智能体系统的动态十分必要.然而，尽管通信网络拓扑包含一个有向生成树，二阶多智能体系统仍然可能实现不了期望的整体行为，因此，研究具有网络通信时延的二阶或高阶动态的多智体系统聚集控制问题是非常有意义的.

文献［15］讨论了一个含有时变通信时延的一阶多智能体系统的聚集控制问题，文中将在文献［15］的基础上考虑一个二阶连续时间多智能体系统跟随者-多领导者聚集控制问题，并利用频域分析、矩阵理论和Nyquist 判据研究网络没有通信限制(零通信时延)和网络含有通信时延情形下的集合聚集控制;最后应用数值实例对新的控制协议进行验证.

1 预备知识

2 控制协议

考虑一个由m 个领导者和N 个跟随者组成的多智能体网络，不妨将这些跟随者记为1，2，…，N，领导者记为N+1，N +2，…，N +m.用一个有向图来模拟这N +m 个智能体之间的通信拓扑关系，N个跟随者之间的通信拓扑记为.为了研究方便，文中将这m 个领导者组成的多边形区域看成一个广义的领导者.在这里，图包含一个有向生成树意味着对任意的跟随者i(i =1，2，…，N)都存在一条由广义领导者到跟随者i(i=1，2，…，N)的有向路径.

领导者k 的动态表示如下:

跟随者i(i=1，2，…，N)的动态特性表示为式中，xi(t)∈Rn，vi(t)∈Rn和ui(t)∈Rn分别表示跟随者i 的位置状态、速度状态和控制输入.为了解决聚集问题，对于第i 个跟随者文中提出两种情形下的分布式控制协议.

1)零通信时延情形

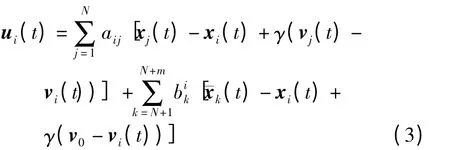
2)有通信时延情形

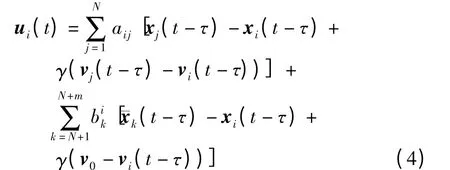
文中的目标是使N 个跟随者都能够聚集于m个动态领导者组成的凸形区域内，即当t ∞时，任意的xi(t)(i=1，2，…，N)到m 个领导者位置状态组成的凸组合co{N+1(t)，N+2(t)，…，N+m(t)}的距离趋向于零，对任意的vi(t)(i =1，2，…，N)最终趋向于领导者的速度状态v0，用数学表达式表示为

式中，In是一个n ×n 的单位矩阵，Im是一个m ×m的单位矩阵，1m、1N分别是m、N 维列向量且其每一个元素都是1表示矩阵的Kronecker 积，=+(1mIN)=［N+1N+2…N+m］，其中，k∈RN×N表示以非负元素(i=1，2，…，N)为对角项的对角矩阵.类似地，将协议(4)代入系统(2)并结合系统(1)写成多变量形式，得:

3 收敛性分析

为了方便得到文中的主要结果，下面先介绍3个重要的引理.

证明 根据文献［16］，只要将多个领导者组成的集合看成一个虚拟的领导者即可证得此引理.

因此有

即证.

引理3［17］对于如下的二次复系数多项式矩阵g(h)=h2+(a1+ib1)h +a0+ib0，i 为虚数单位，a0、a1、b0、b1∈R，则g(h)的根位于左半平面当且仅当a1＞0 且

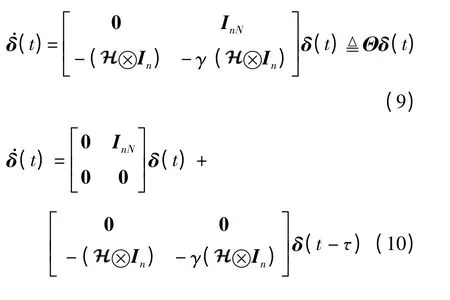
文中主要结果如下所示.

定理1 对于多智能体系统(1)、(2)，在控制协议(3)下，如果网络通信拓扑包含一个有向生成树且γ ＞γ*，其中，

ηi是矩阵的第i 个特征根，则所有的跟随者能够聚集于多个动态领导者组成的凸多边形区域内，即

证明 由式(9)可知，N 个跟随者能够聚集于m 个领导者组成的凸形区域内当且仅当Θ 的特征根全小于零.下面通过解det(I2nN-Θ)=0 来寻找Θ 的特征根.注意到

比较式(12)和(13)可得

故Θ 的特征根满足

令ηi=α+βi，α，β∈R+，代入式(14)得

根据引理3 可知，式(14)的根位于左半平面当且仅当γα ＞0 且又因为γ ＞0，结合引理1可知当图包含一个有向生成树且γ ＞γ*时i±的实部均小于零，其中γ*在式(11)中给出.故当t ∞时，δ(t) 0，则系统(9)渐近稳定.从而，x(t)

下面研究当跟随者接收的邻居的状态信息含有通信时延时的聚集控制问题.

定理2 对于多智能体系统(1)、(2)，在控制协议(4)下，如果耦合系数γ ＞0 且连接拓扑包含一个有向生成树，则所有的跟随者能够聚集于多个动态领导者组成的凸多边形区域内的充分条件是

证明 对系统(10)的分量两边取拉普拉斯变换得:

式中，ξ(s)和ζ(s)分别是ξ(t)和ζ(t)的拉普拉斯变换.上述方程可改写为

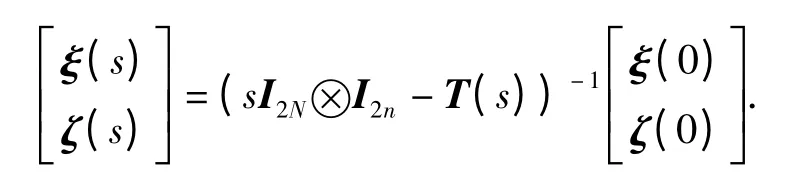
式中

因此，得到关于T(s)的特征方程

注意到

结合式(16)和(17)得

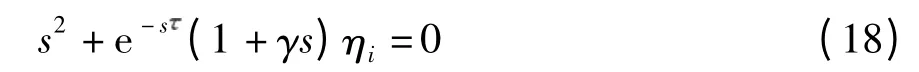
从而可以得到

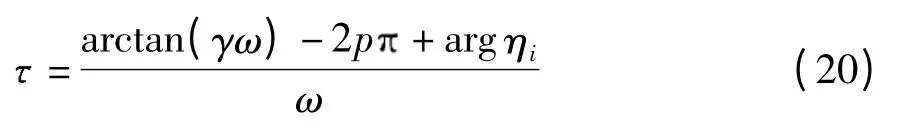
对式(19)两边取模得

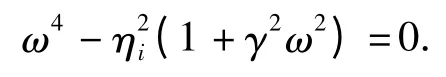
因此

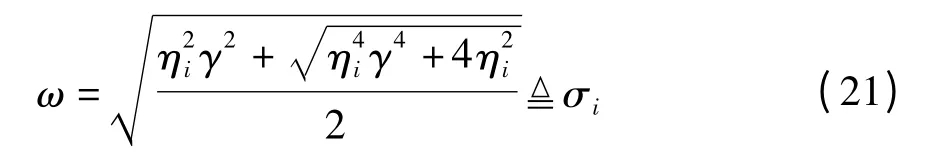
结合式(20)和(21)可得

类似地，对于ω ＜0，可以得到与ω ＞0 相似的结论.因此，只要＜*，式(16)的根都位于左半平面.故当t ∞时，δ(t) 0，则系统(10)渐近稳定.从而

接下来证明最终每个跟随者都能进入到动态领导者组成的凸形区域内.因证明过程与定理1 后面部分类似，故略去.

4 数值实例

本节给出两个数值实例来验证文中主要结果.图1 表示两个具有多个领导者的通信拓扑图1、1和2、2.显然，图1和2都包含一个有向生成树.

例1 采用图1(a)所示的多智能体网络，其由2 个领导者和5 个跟随者组成，假定每个智能体都在一个水平线上运动且智能体之间的通信没有时延.取γ=1，给定领导者的初始条件¯x1(0)=0 m，2(0)=1 m，v0=0.5 m/s.跟随者的位置和速度状态初始条件分别在区间［2，10］和［1，5］中随机选取.图2 给出了5 个跟随者跟随2 个领导者的位置和速度状态轨迹.由图2 可知，5 个跟随者都能够聚集于领导者1 和2 组成的长度为1 的动态区间内.

图1 两个有向图的拓扑结构Fig.1 Two directed interaction topologies

图2 图1 下2 个领导者和5 个跟随者的状态轨迹Fig.2 State trajectories of two leaders and five followers under topology1

例2 采用图1(b)所示的多智能体网络，其由4 个领导者和5 个跟随者组成.假设智能体之间的通信有时延且它们都在一个平面上运动.给定跟随者和领导者的初始位置和速度条件:

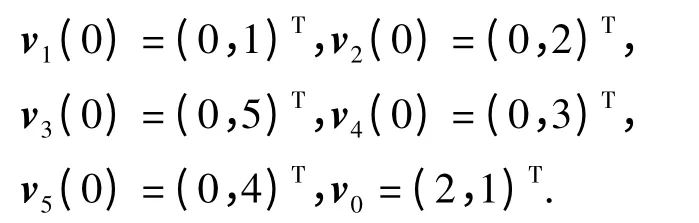
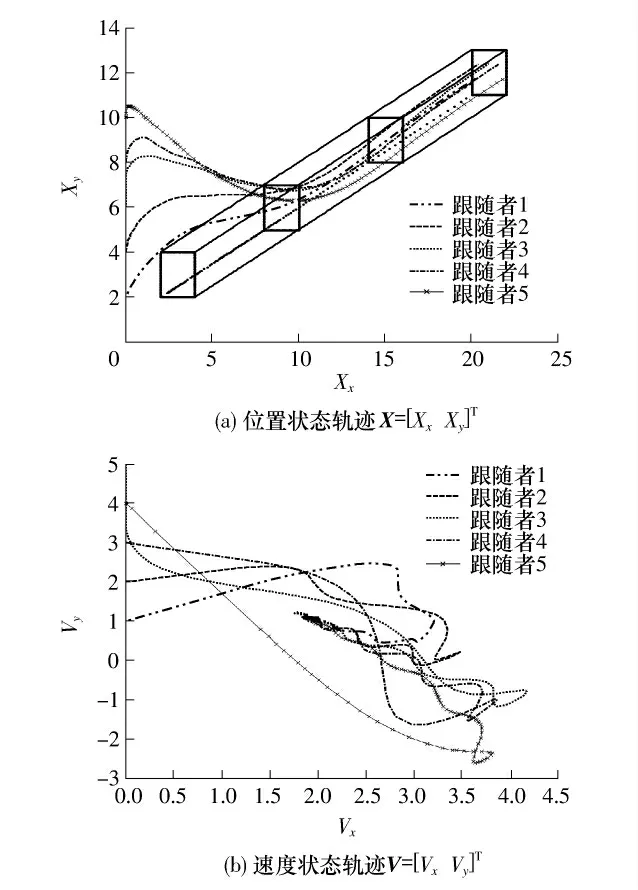
图3 在时延 =0.2000 和通信拓扑2 下的5 个跟随者和4 个领导者的状态轨迹Fig.3 State trajectories of five followers and four leaders under the topology2 and =0.2000

图4 在时延 =0.2450 和通信拓扑2 下的5 个跟随者和4 个领导者的状态轨迹Fig.4 State trajectories of five followers and four leaders under the topology2 and =0.2450

5 结语

文中分析了一个二阶连续时间多智能体系统跟随者-多领导者聚集控制问题.针对网络零通信时延和含有网络通信时延的情形，分别得到所有的跟随者最终都能进入由多个动态领导者组成的凸多边形区域内的充分条件.结果表明，只要智能体之间的通信时延不超过最大时延上界，所有的跟随者最终都能够聚集于多领导者组成的凸组合内.数值仿真实例表明了文中所提方法的可行性和正确性.在实际的通信网络中，时延可能是时变的，也可能是多时变的，通信拓扑可能是变化的，因此，网络含有时变时延或者变化的通信拓扑是我们进一步研究的问题.

［1］Fax J A，Murray M.Information flow and cooperative control of vehicle formations［J］.IEEE Transactions on Automatic Control，2004，49(9):1465-1476.

［2］Yang P，Freeman R，Lynch K.Multi-agent coordination by decentralized estimation and control［J］.IEEE Transactions on Automatic Control，2008，53(11):2480-2496.

［3］Saber R O.Flocking for multi-agent dynamic systems:algorithms and theory［J］.IEEE Transactions on Automatic Control，2006，51(3):401-420.

［4］Saber R O，Murray R M.Consensus problem in networks of agents with switching topology and time-delays ［J］.IEEE Transactions on Automatic Control，2004，49(9):1520-1533.

［5］谭拂晓，关新平，刘德荣.具非平衡拓扑结构的多智能体网络系统一致性协议［J］.控制理论与应用，2009，26(10):1087-1092.Tan Fu-xiao，Guan Xin-ping，Liu De-rong.Consensus protocol in networked multi-agent systems with non-balanced topology［J］.Control Theory ＆ Applications，2009，26(10):1087-1092.

［6］Rew W，Beard R W，Kingston D B.Multi-agent Kalman consensus with relative uncertainty［C］∥Proceedings of the American Control Conference.Portland:IEEE Press，2005:1865-1870.

［7］曾明，危阜胜，陈冠升，等.面向目标跟踪的WSN 协同调度策略及拓扑控制［J］.华南理工大学学报:自然科学版，2010，38(6):60-65.Zeng Ming，Wei Fu-sheng，Chen Guan-sheng，et al.Collaborative scheduling strategy and topology control for target tracking in wireless sensor networks ［J］.Journal of South China University of Technology:National Science Edition，2010，38(6):60-65.

［8］Sorrentino F，Bernardo M D，Garofalo F.Synchronizability and synchronization dynamics of weighed and unweighed scale free networks with degree mixing［J］.International Journal of Bifurcation and Chaos，2007，17(7):2419-2434.

［9］Duan Z S，Chen G R，Huang L.Complex network synchronizability:analysis and control ［J］.Physical Review E，2007，76(5):056103/1-5.

［10］Hu J P，Yuan H W.Collective coordination of multiagent systems guided by multiple leaders［J］.Chinese Physics B，2009，18(9):3777-3782.

［11］Li Z K，Ren W，Liu X D，et al.Distributed containment control of linear multi-agent systems with multiple leaders and reduced-order controllers［C］∥Proceedings of 50th IEEE Conference on Decision and Control and European Control Conference.Orlando:IEEE Press，2011:771-776.

［12］Cortes J，Bullo F.Robust rendezvous for mobile autonomous agents via proximity graphs in arbitrary dimensions［J］.IEEE Transactions on Automatic Control，2006，51(8):1289-1298.

［13］Su H S，Wang X F，Chen G R.Rendezvous of multiple mobile agents with preserved network connectivity［J］.Systems ＆ Control Letters，2010，59(5):313-322.

［14］Shi G，Hong Y G.Global target aggregation and state agreement of nonlinear multi-agent systems with switching topologies ［J］.Automatica，2009，45(5):1165-1175.

［15］刘学良，胥布工，谢立华.具有通信时延的跟随者-多领导者聚集控制［J］.控制理论与应用，2012，29(5):649-654.Liu Xue-liang，Xu Bu-gong，Xie Li-hua.Multileader set aggregation control of multi-agent systems with communication delays［J］.Control Theory ＆ Applications，2012，29(5):649-654.

［16］Hu J P，Hong Y G.Leader-following coordination of multi-agent systems with coupling time delays ［J］.Physica A，2007，374(2):853-863.

［17］Parks P C，Hahn V.Stability theory ［M］.New York:Prentice Hall，1993.