线阵TDI探测器成像中扫描速度偏差影响

李 军，修吉宏，黄 浦，李友一

(中国科学院长春光学精密机械与物理研究所，中国科学院航空光学成像与测量重点实验室，吉林长春130033)

1 引言

线阵TDI探测器在现代靶场测试和航空、航天遥感遥测等领域具有广泛的应用，可在低照度时捕获目标的相关信息。通过多级时间积分来延长积分曝光时间，使用线阵TDI探测器不仅大大提高相机光通量，而且提高了相机的灵敏度和信噪比，降低了光能量对相机相对孔径的要求，有利于降低重量和成本［1］。

由于TDI探测器的工作方式比较特殊，要求它的同步脉冲周期与目标的运动速率应严格同步，否则无法保证同一列上的每一个像元都能对同一地面目标成像，从而造成在延迟积分时间内的像移。事实上，由于扫描成像系统存在速度波动，实现严格同步是不可能的。因此以系统的运动调制传递函数为基础，提出对扫描速度波动程度的限制条件，可为扫描系统设计提供依据。近年来的研究结果表明，调制传递函数仍然是评价光学系统TDI探测器成像质量的可靠方法，因此分析扫描速度波动与系统运动调制传递函数的关系，并以此提出对扫描速度偏离程度进行限制是合理有效的［2－4］。本文以某型航空相机为基础，给出系统达到指定运动调制传递函数时，扫描速度与期望值间偏差的限制条件，为航空相机中扫描系统提供设计输入条件。

2 运动光学传递函数推导

在航空相机扫描成像过程中，线阵TDI探测器的同步脉冲周期需要与地面景物在像面上的移动速度对应，其满足式(1)约束。其中，T为线阵TDI探测器的同步脉冲周期，b为探测器像元尺寸，f光学系统焦距，θ0为期望的镜筒旋转的角速度。

当扫描速度与探测器的同步脉冲周期完全匹配时，地面景物在像面成像与探测器间是保持相对静止的，不会造成成像质量下降。但航空相机工作时受轴系摩擦、载机横滚等多种因素影响，镜筒的实际转速θ会与期望值θ0间存在偏差，这种偏差会导致线阵多级TDI探测器不同级敏感区对目标景物的临近区域进行曝光，降低系统的分辨能力。因此在应用线阵TDI探测器进行航空相机系统设计时需要考虑该偏差的影响。

扫描速度与期望值对系统成像质量的影响可以使用运动光学传递函数描述。

对于线阵多级TDI探测器，第i级敏感区在像面上的位置为xi_det=(i－1)·b，因此镜筒扫描速度偏差引起的目标景物图像相对探测器的位移函数为

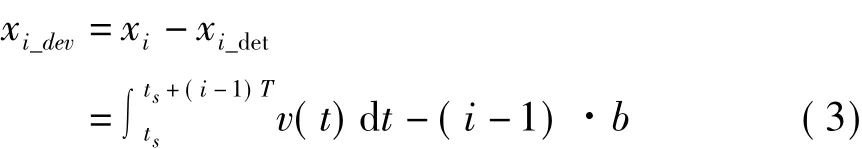
xi_dev描述了使用多级TDI探测器进行成像时目标景物图像在像面上的分布，将其称为图像位置偏差函数。由图像位置偏差函数可计算出像面不同位置出目标图像分布的概率密度函数p(x)。探测器同步脉冲周期与镜筒扫描速度不匹配只导致一个方向的图像分辨能力下降，使用线扩散函数即可描述图像分辨能力的下降。概率密度函数p(x)即为镜筒速度不匹配产生的线扩散函数，对其进行傅里叶变换可得到镜筒扫描速度偏差产生的运动光学传递函数，如式(4)所示，其中ω为空间角频率。

文献［5］中给出了基于统计距的由图像位置偏差函数计算系统运动光学传递函数的算法。本文中描述的图像位置偏差xi为离散量，系统运动光学传递函数可用式(5)进行计算，其仅为xi的函数。其中，mn为图像位置偏差的n阶统计距。

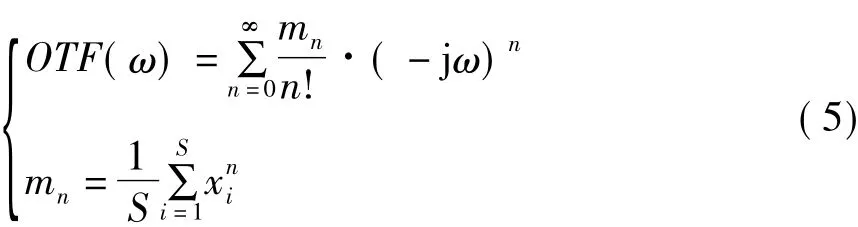
当图像位置偏差函数xi无法用解析式进行表示时，为获得系统的运动光学传递函数需要计算无穷级数。在实际应用中需要进行N阶截断，截断误差为［5］:，其中N为偶数。

在实际应用中，同步脉冲周期T一般为亚毫秒量级，镜筒扫描速度在T时间内几乎不变，可认为在T时间内为恒定值。此时，像面位置偏差函数xi_dev可改写为式(6)形式。

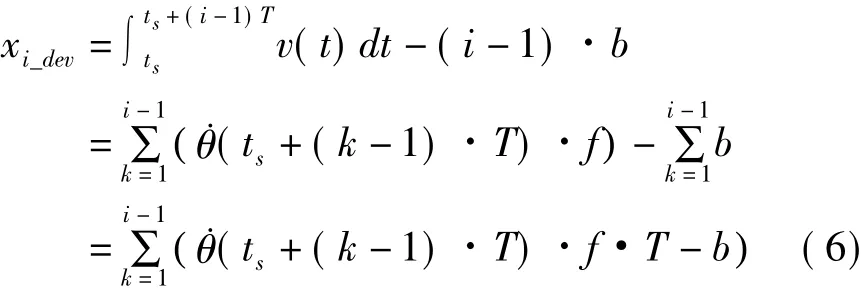
由式(1)可得:

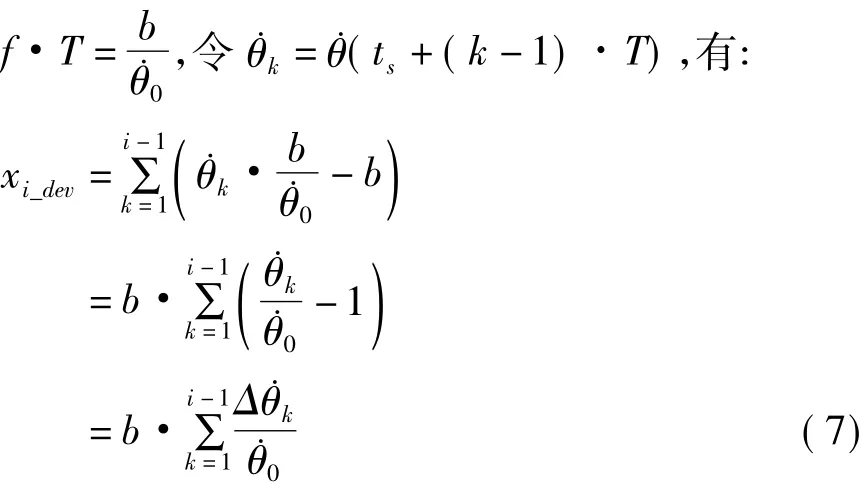
由式(7)看出，探测器不同级敏感元件对应的图像位置偏差仅与探测器像元尺寸、探测器积分级数和速度波动的相对偏差有关，而与系统的焦距无关。另外，Δθk还依赖于曝光起始时刻ts，系统的运动光学传递函数为一个随机过程［6］。在获得系统的运动光学传递函数后，可使用式(8)获得系统的运动调制传递函数。

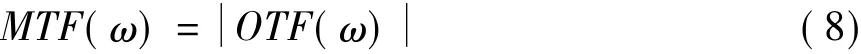
3 数值计算及实验结果分析

3.1 数值计算结果

首先，计算镜筒转速偏差为恒定值时系统运动调制传递函数结果。选择镜筒扫描速度期望值为θ0=10°/s，探测器器像元尺寸为b=24 μm，探测器积分级数为I=6，相对偏差误差分别为5%、10%和15%，计算不同相对偏差误差对应的运动调制传递函数。图1(a)为相对误差为10%时选择不同像元尺寸对应的数值计算结果，可看出在扫描转速相对偏差固定的情况下，选择像元尺寸大的探测器并未提高系统在空间乃奎斯特频率处的运动调制传递函数;相反，在相同空间分辨率处，像元尺寸越大对应的光学系统运动传递函数下降越快。这是因为在相同条件下像元尺寸大对应探测器同步脉冲周期长，对应的图像位置偏差也变大。图1(b)为像元尺寸相同时不同相对误差对应的系统运动调制传递函数，可以看出系统运动调制传递函数随相对误差增大而下降。因为相对误差越大，在相同的同步脉冲周期内图像位置偏差也越大。

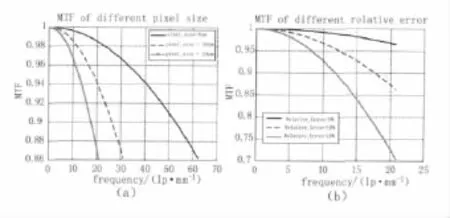
图1 相对误差恒定时系统运动调制传递函数

其次，计算镜筒扫描速度波动对系统运动调制传递函数影响。图2给出了镜筒转速稳定时的某一次测量结果，镜筒的扫描速度围绕期望值10°/s上下波动。式(7)中图像位置偏差函数xi_dev与拍照起始时刻ts相关且为随机变量，由此计算的系统运动调制传递函数是依赖拍照起始位置的随机过程。拍照起始时刻在0～2 s范围内选择，计算不同速度波动对应的系统运动调制传递函数。图3给出了探测器积分级数为32，不同曝光起始时刻对应的运动调制传递函数曲线。从图3中看出，在不同时刻开始曝光，系统运动调制传递函数差别很大，为给出合理的结果应计算调制传递函数的概率为99%的界限，如图3中菱形曲线所示结果，即在不同起始时刻曝光时99%的调制传递函数高于此界限。

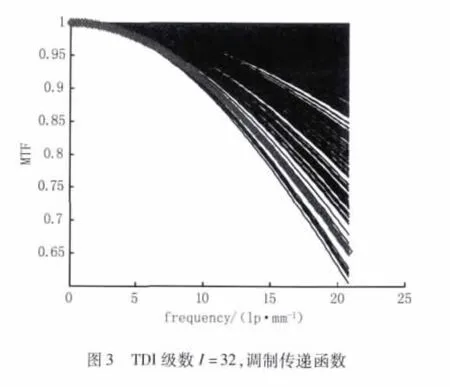
使用RMS值可描述镜筒转速的波动程度，计算镜筒转速不同RMS值对应的调制传递函数结果，可了解系统传递函数对镜筒转速波动的限制。图4给出探测器积分级数为16，镜筒扫描速度RMS值为0.045、0.089、0.178、0.357 对应的传递函数 99%界限。看出随扫描速度波动增大，在截止频率处系统运动调制传递函数急剧下降。

图4 TDI级数I=16，调制传递函数

计算探测器不同级数时，在截止频率处获得指定的运动调制传递函数值所对应的扫描速度波动程度，可用于指导制定扫描速度控制系统稳定精度的量化指标，为控制系统设计提供设计输入依据。表1给出了不同积分级数、截止频率处不同调制传递函数值所对应的扫描速度相对波动程度。

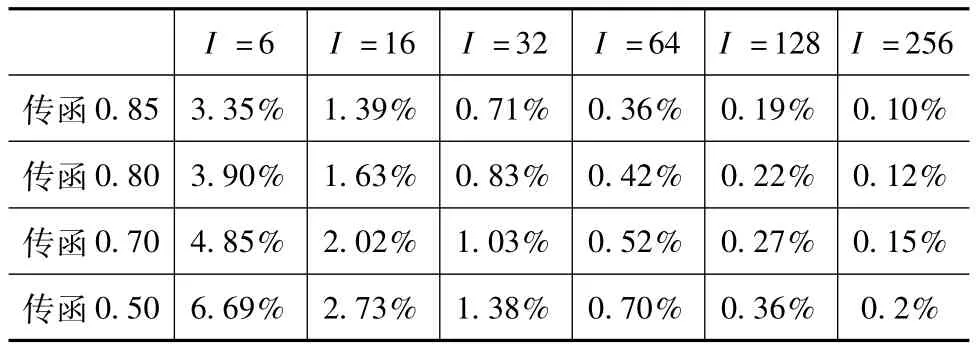
表1 不同级数对应扫描速度相对精度

数值计算的结果表明，影响系统截止频率处的运动调制传递函数值的主要因素为探测器积分级数和扫描速度的相对误差。当传递函数要求相同时，镜筒相对误差容限与积分级数近似成反比。提高探测器积分级数可以提高系统的探测灵敏度和信噪比，但对扫描速度的转速稳定精度要求也大大提高。在进行系统设计选择探测器积分级数时要考虑控制系统所能达到的控制性能，否则系统将很难达到设计的分辨能力。

3.2 实验测量结果

为验证线阵多级TDI成像中扫描速度波动产生的运动调制传递函数计算方法的正确性，使用线阵扫描装置对探测器截止频率处的传递函数值进行了测量。先测量静态系统光学传递函数，再测量动态扫描成像时系统调制传递函数，通过两者运算可得到系统的运动调制传递函数。但对于线阵TDI探测器而言，无法测量静态光学传函，因此使用系统镜头的传递函数代替系统的静态光学传函，此时得到的系统运动调制传递函数包含了探测器离散化的影响。这可能导致测量结果偏低。

实验装置如图5所示，系统的焦距f=119.8 mm，探测器像元为0.024 mm，探测器级数选择为I=16，探测器同步脉冲周期为T=1.148 ms，转台转动速度期望值为10°/s。图6(a)为光学镜头的调制传递函数测量结果，在截止频率处的传递函数为0.30。图6(b)为拍摄的黑白等间隔条纹构成的鉴别率板图像，所以其对应的调制对比度函数为系统的CTF，需将其转换为MTF。将换算后，系统扫描成像在截止频率处对应的调制传递函数值为0.26，即系统的运动调制传递函数为0.87，而使用数值计算获得的运动调制传递函数为0.90。因此，数值计算与实际测量结果间的相对误差为3.33%，说明文中介绍的运动调制传递函数计算方法是有效的。

图6 光学传递函数实验测量结果

4 结论

本文推导介绍了线阵TDI探测器扫描成像中扫描速度偏差与系统运动光学传递函数的关系，通过数值计算方法分析了扫描速度偏差对系统调制传递函数影响。数值计算的结果表明，影响线阵TDI探测器成像系统截止频率处的运动调制传递函数值的主要因素为探测器积分级数和扫描速度的相对误差。当传递函数要求相同时，镜筒相对误差容限与积分级数近似成反比。提高探测器积分级数可以提高系统的探测灵敏度和信噪比，但对扫描速度的转速稳定精度要求也大大提高。在进行系统设计选择探测器积分级数时要考虑控制系统所能达到的控制性能，否则系统将很难达到设计的分辨能力。实验结果表明，使用统计的方法计算扫描速度波动的影响是科学合理的，数值计算结果与实际测量结果相对误差在5%以内，本文给出的扫描速度波动的限制条件计算方法，为航空相机总体传递函数分配提供有效支持。

［1］Yang Bingxin．Research of the static MTF for the aerospace TDICCD camera［J］．Spacecraft Recovery ＆ Remote Sensing，2004，25(3):22 －24．(in Chinese)

杨秉新．航天TDICCD相机静态调制传递函数的研究［J］．航天返回与遥感，2004，25(3):22 －24．

［2］Zhang Lin，Wu Xiaoqin，Tang Gongmin．Analysis of synchronization error for time delayed integration(TDI)CCD imaging system based on MTF［J］．Journal of Applied Optics，2006，27(2):167 －170．(in Chinese)

张林，吴晓琴，汤宫民．基于MTF的时间延迟积分CCD成像系统同步误差分析［J］．应用光学，2006，27(2):167－170．

［3］Wu Hongshen，Pan Ning，Zhai Linpei．Image motion compensation error analysis for TDI CCD panoramic aerial camera［J］．Optics and Precision Engineering，2003，11(6):545 －549．(in Chinese)

吴宏圣，潘凝，翟林培．TDI CCD全景式航空相机的像移补偿误差分析［J］．光学 精密工程，2003，11(6):545－549．

［4］O Hadar，I Dror，N S Kopeika．Image resolution limits resulting from mechanical vibration．Part IV:real time numerical calculation of optical transfer functions and experimental verification［J］．Opt．Eng．，1994，33(2):566 －578．

［5］A Stem，N S Kopeika．Analytical method to calculate optical transfer functions for image motion using moments and its implementation in image restoration［J］．SPIE，2004，2827:191－202．

［6］A Papoulis．Probability，Random Variables，and Stochastic Processes［M］．New York:McGraw － Hill，1984．

［7］O Hadar，M Fisher，N S Kopeika．Numerical calculation of image motion and vibration modulation transfer function［J］．SPIE 1991，1482:79 －91．