基于Matrix Pencil的低频振荡辨识及PSS优化配置研究

张军财 金 涛

（福州大学电气工程与自动化学院，福州 350108）

电力系统低频振荡的传统分析方法是建立在小干扰稳定分析基础上的，在平衡点线性化处理得到近似的状态空间方程，继而求解系统矩阵的特征值。互联的电力系统无疑是庞大而复杂，为高阶系统，参数繁多。因而，建立准确的数学模型并求解高维数的系统矩阵无疑是非常困难的[1]。基于辨识的振荡模态识别方法能够直接从系统输出的受干扰轨迹的信号中提取系统的模态信息。

PSS抑制电力系统低频振荡是目前公认的最为经济的，有效一种手段[2]。在PSS优化设计过程中除了PSS参数设计重要外，PSS的地点配置亦是一个重要课题[3]。在实际电力系统中每台机组都安装PSS是不现实的，而且过多的控制器之间也有可能产生耦合效果，会降低控制效果。因此，研究如何在复杂多机系统的低频振荡中PSS的优化配置是有意义的，为合理的安装PSS阻尼控制器提供指导，提高电力系统的稳定性。在多机电力系统的低频振荡中，通常认为对其中参与振荡主导模态的发电机组安装PSS进行控制。

在对PSS配置地点的问题研究中，通常是基于特征值分析法的基础上，对系统矩阵以及控制和输出矩阵进行一定的变化，分解出主导振荡模态在各输出量上可观性向量和控制量上的可控性向量。此类方法有最早的右特征向量法[4]，以及后来发展而来的参与因子法等[5-6]。然而特征值分析是需对电力系统进行建模前提下进行的，这必须要有所研究的电力系统的完备的参数以及复杂而处理、计算，显然不太现实。文献[7]提出用传递函数留数进行PSS和SVC的选址方法，无需对电力系统建模，能定量评价系统状态变量的可控性和可观性指标。

在给定的已知干扰信号情况下，本文研究了基于Matrix Pencil算法的建立系统低阶近似传递函数，并对建立的系统低阶近似传递函数输出与仿真系统输出对比验证该方法的有效性。并在此基础上，对系统传递函数基于SVD分解分析系统各输出和输入量对电力系统的主导振荡模态的影响，找出对主导振荡模态能观性显著的输出状态量，和对主导振荡模态能控性显著的输入量，从而找出最适合的PSS安装机组，对分析结果进行仿真试验验证其有效性。

1 基于Matrix Pencil的传递函数辨识

对于一个单输入单输出的线性时不变系统，输入输出满足如下关系：Y( s)为输出，G( s)为传递函数，I( s)为输入。

因为是线性时不变系统，传递函数G( s)可写成含特征值和对应留数的形式，如下：

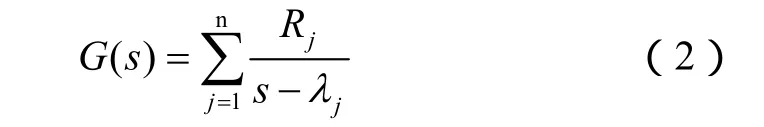
式中，jλ为系统特征值，Rj对应的留数。

对于输入I( s)，可给予如下特定特征的信号，由一系列延迟信号相加而成，表示如下：

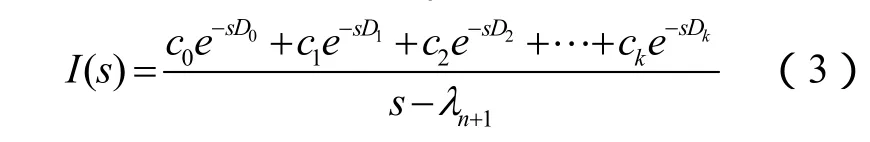
式中，D0=0，λn+1输入信号特征值，Dk为延迟信号时间常数，ck延迟信号的幅值。

则输出Y( s)根据是式（1），求得为

按部分式展开得：

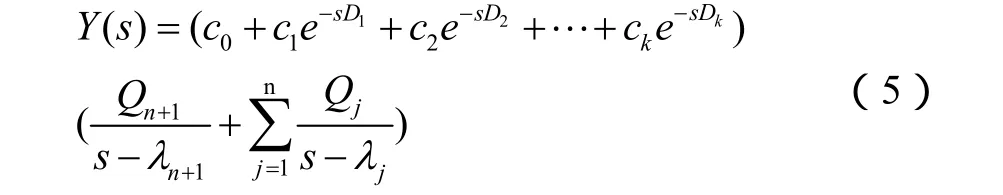
其中：

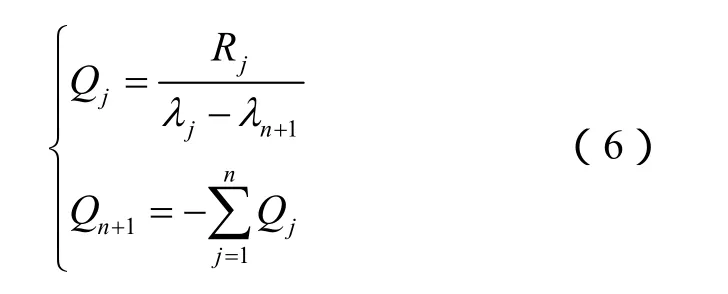
对Y( s)进行拉普拉斯变换，

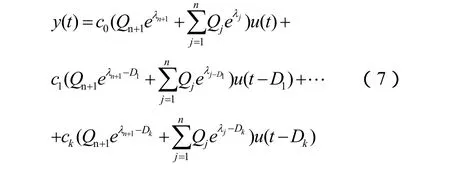
在t≥Dk时，输出信号y( t)可以简化为下式：

对输出信号，可以利用Matrix Pencil算法对获得的输出数据进行低频振荡辨识分析，求得各振荡模态的振荡频率、阻尼系数、振荡幅值和相对相位等有关信息。

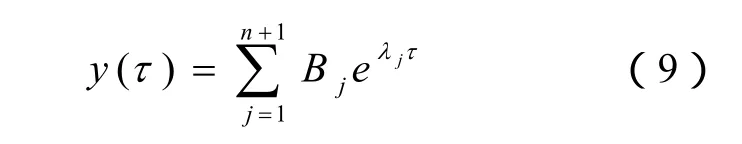
将辨识得到的输出信号与式（8）对比，得

因此，传递函数留数Rj则据下式可求：

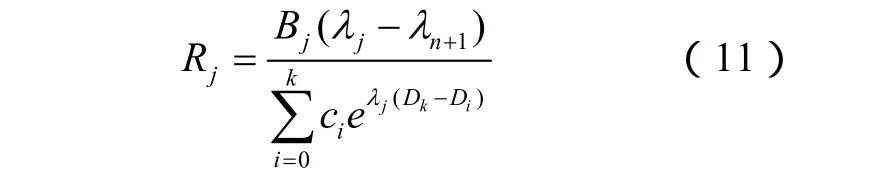
在本文中对于输入信号I( s)，令 λn+1=0，c1=-c0，ck=0 （ k = 2 ,3,…） 。所以输入信号简化为I(s)=

2 奇异值分解分析PSS优化配置

n×n的多输入多状态变量输出之间的传递函数有如式（12）成立

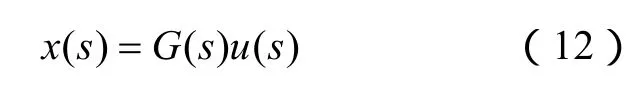
对传递函数进行奇异值分解如下：

U(s)=[U1( s), … ,Un(s )]为G(s)奇异值分解后左奇异值向量，V(s)=[ V1( s) ,… ,Vn( s )]为右奇异值向量，且满足

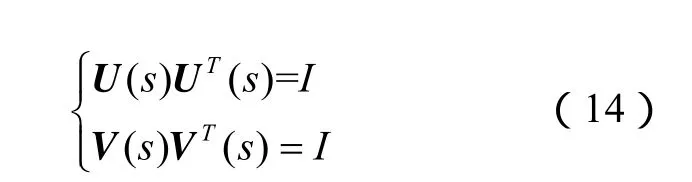
Λ(s) = diag (Λ1(s ),… ,Λn(s ))为G(s)奇异值分解得到的奇异值矩阵。

如此，左右奇异值向量则构成n维状态输出空间与n维输入空间的标准正交基，Λ(s)则是输入向量和输出状态在各自的酋空间中的各对应坐标值之间的增益。

在低频振荡中，只考虑低频振荡主导振荡模态i，其振荡频率 w ，将s=jw带入G(s)得G(jw)，得到的G(jw)即为主导振荡模态的矩阵。对G(jw)进行奇异值分解如下：

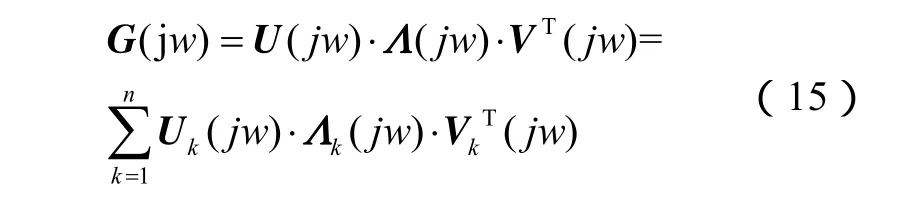
式中，Λ(jw)是由G(jw)的奇异值构成

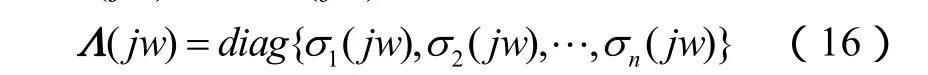
且满足有关系：

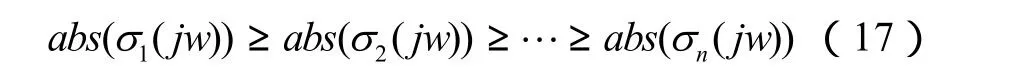
U(jw)和VT(jw)则为对应于G(jw)的左、右奇异值向量。

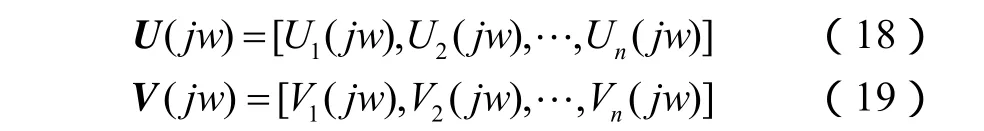
若abs(σ1(j w))≫ abs(σ2(j w))

则有：

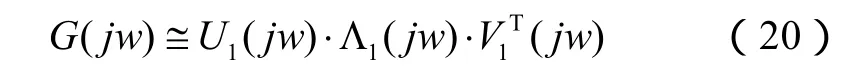
U1(j w)反映了输出状态量x对模态i的能观性，反映了输入量对模态i的能控性。

3 仿真实验分析

3.1 求辨识传递函数

对于如图1所示的4机2区域系统，对机组1的励磁参考电压在1s时刻施加幅值为0.05，持续时间为0.1s的方波脉冲干扰，则输入信号拉普拉斯变换为I( s)=。用Matrix Pencil方法分别对干扰消失后的 4机转速变化曲线拟合求取y(τ)。求出的信号极点如图2所示，从此图可以看出有一对极点在复数图的右半平面，系统不稳定。

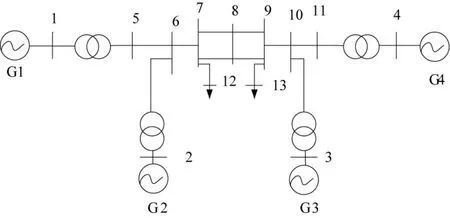
图1 4机2区域电力系统

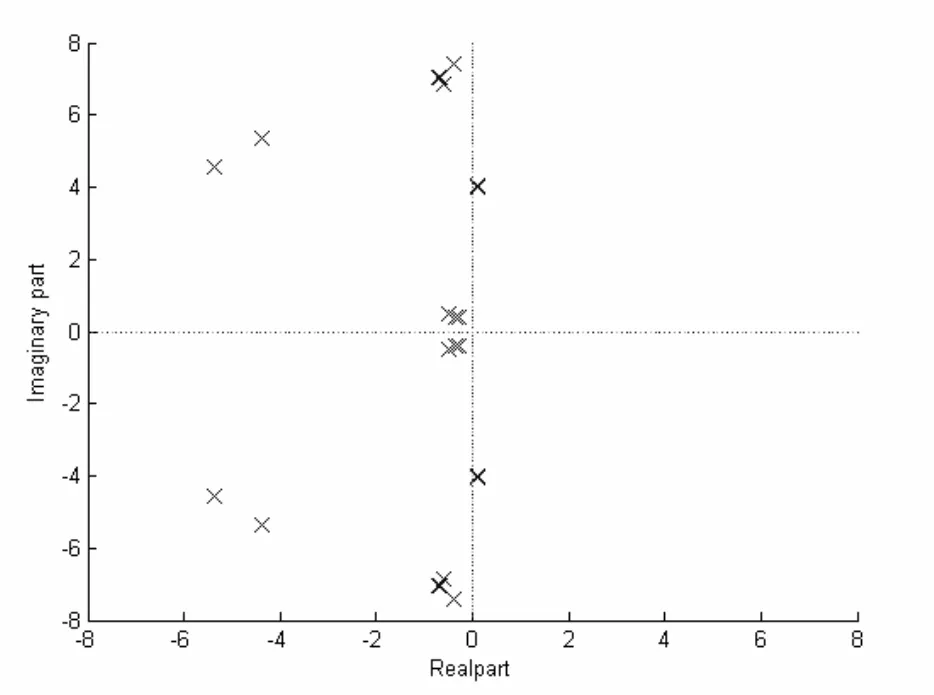
图2 信号极点分布图

根据前文中的方法求取低阶近似辨识传递函数，取4阶近似。分别以G11、G12、G13、G14表示以机 1的励磁参考扰动电压为输入，4台发电机的转速变化为输出建立的传递函数。表1给出了辨识传递函数的参数，Num、 Den分别为传递函数分子、分母。

表1 机1的励磁参考扰动电压为输入，4机的转速变化为输出的传递函数

将求得的辨识传递函数给以的输入和系统对于4机2区域系统的机组1的励磁参考电压给以的输入一样：在 1s时刻受到幅值为 0.05，持续为 0.1s的方波脉冲干扰信号输入，然后对比输出如图3所示。从图3可以看出，降阶辨识传递函数的输出与4机 2区域系统的转速变化输出基本一致。在开始受到干扰的时刻出时段，输出误差比较大，原因是辨识传递函数是降阶的拟合，忽略掉了不是弱阻尼的振荡模式，在干扰后一段时间（4～5s后），拟合度越来越好，原因是弱阻尼振荡模式衰减较快，经过一段时间衰减到很小。

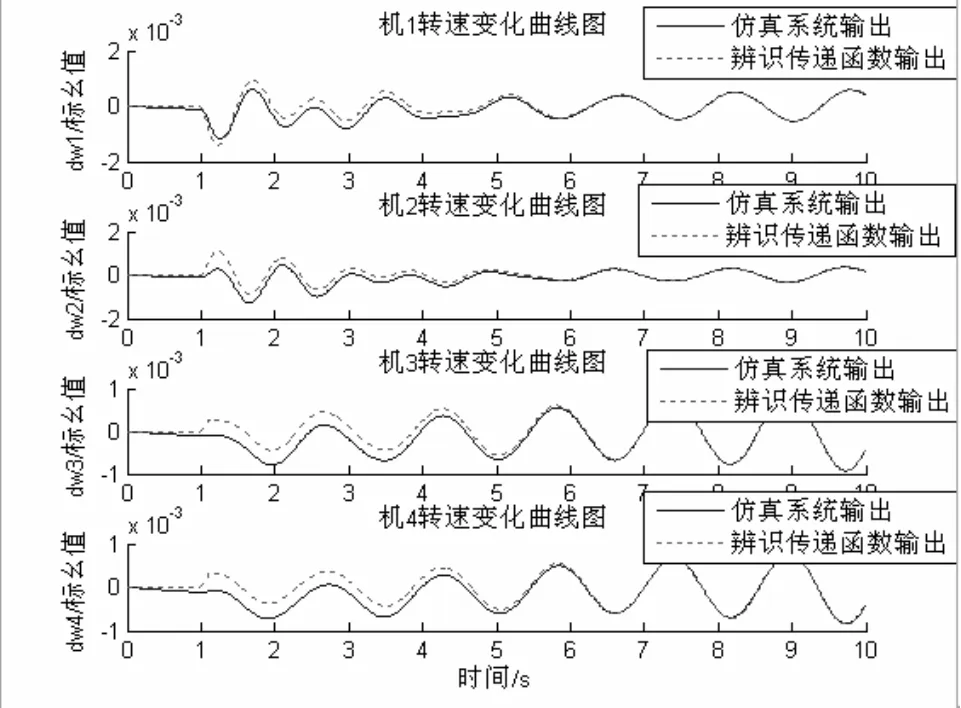
图3 辨识传递函数输出与4机2区域系统输出比较

用同样的方法，分别以机2、3、4的励磁参考扰动电压为输入，4机组的转速变化为输出求取低阶近似辨识传递函数，建立4×4的多输入多输出系统的传递函数。

3.2 SVD分解分析PSS配置

用 Matrix Pencil分析输出干扰轨迹得到振荡主导模态的角频率w=2×pi×0.65rad/s。图4是4×4低阶近似辨识传递函数的幅频特性曲线特性曲线，从图4也可以看出系统的在角频率w=4.095rad/s附近最大。

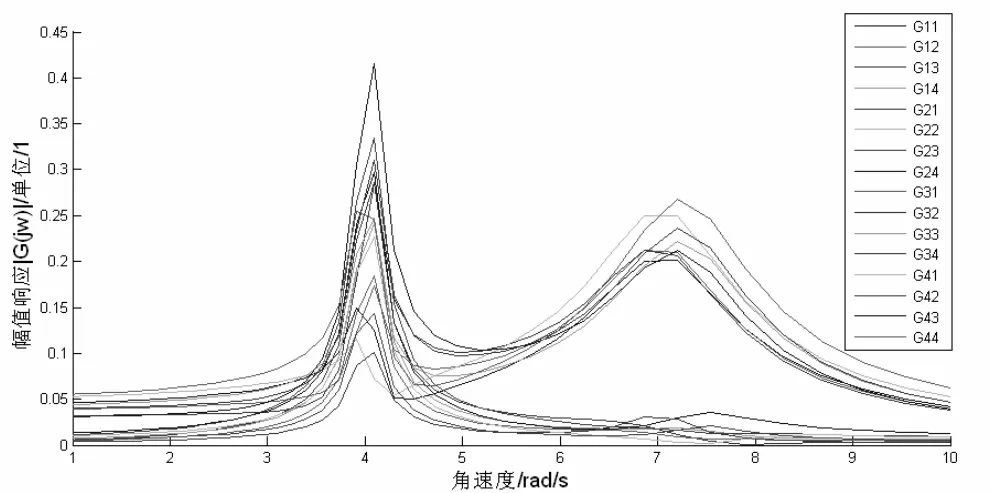
图4 4×4传递函数的幅频特性曲线

基于SVD分解主导振荡模态的矩阵G(jw)可得到Λ(jw)、、分别如下：

Λ( jw)=diag(1.1555, 0.1198,0.0947,0.0170)

左奇异向量

右奇异向量

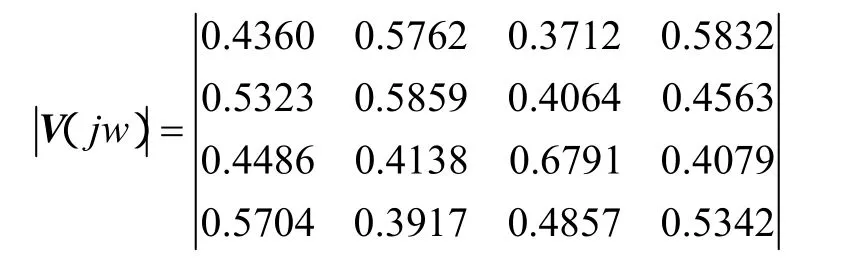
对应于最大奇异值，从左右奇异值向量分别取绝对值后的第一列，可以看出，机3的主导模态的能观性最好，机2的主导模态的能观性最差；机4的主导模态的能控性最好，机1的主导模态的能控性最差。本文的 PSS的反馈信号采用各自的机组转速变换信号，因此将左右奇异向量点乘取绝对值，并除以向量中最大的值，得[0.5936,0.4254,0.9626,1]。从该向量可以看出配置PSS效果好的机组是机3、4，效果差的是机1、2。

对上述分析结果进行仿真验证。分别在机1、2、3、4上单独装设以各自的转速变化为输入的PSS控制器。PSS采用IEEE标准的单通道PSS模型，结构框图如图5所示，包含放大环节、隔直环节、两个相位补偿环节和限幅环节四个环节。本文实验设计PSS参数采用留数法设计，得到的各机PSS参数见表2。

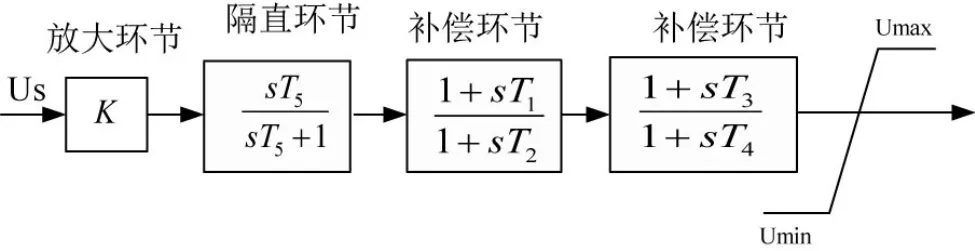
图5 IEEE单通道PSS模型

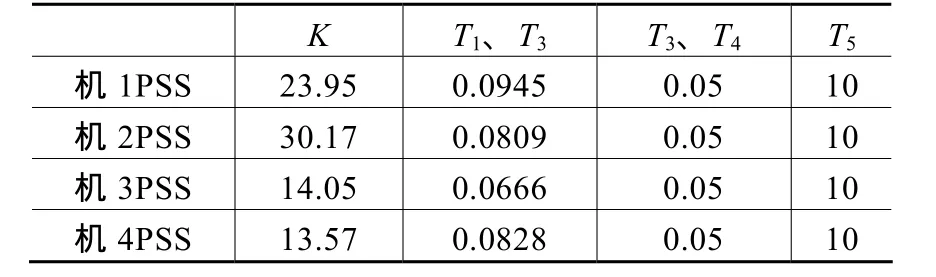
表2 4机PSS的参数表

实验条件则仍在机1上施加小脉冲干扰，1s时刻受到幅度为0.05，持续时间为0.1s励磁电压干扰信号，观察其各自抑制振荡效果。图6是显示的是联络线上功率振荡曲线图。从图6中的PSS效果可以看到，在机4上装设PSS效果最好，其次是机3，机1、2效果不好，不能很好地抑制区域间振荡。说明基于 SVD分解法的能够定量地分析多机系统中各机组参与振荡主导模态的程度，并据此配置 PSS是实现低频振荡抑制是合理的。

图6 不同PSS配置点下的联络线上功率振荡曲线

电力系统安全稳定运行一般要求系统阻尼比不小于0.05，大约5个周波振荡要衰减至很小。考虑到机3、4参与区间振荡模式程度深，于是在机3、4装PSS并设计好参数。仿真运行比较无PSS、全部装PSS，机3、4装PSS联络线功率振荡曲线如图7所示。从图可知在机3、4上装可以抑制低频振荡，满足稳定运行的要求。

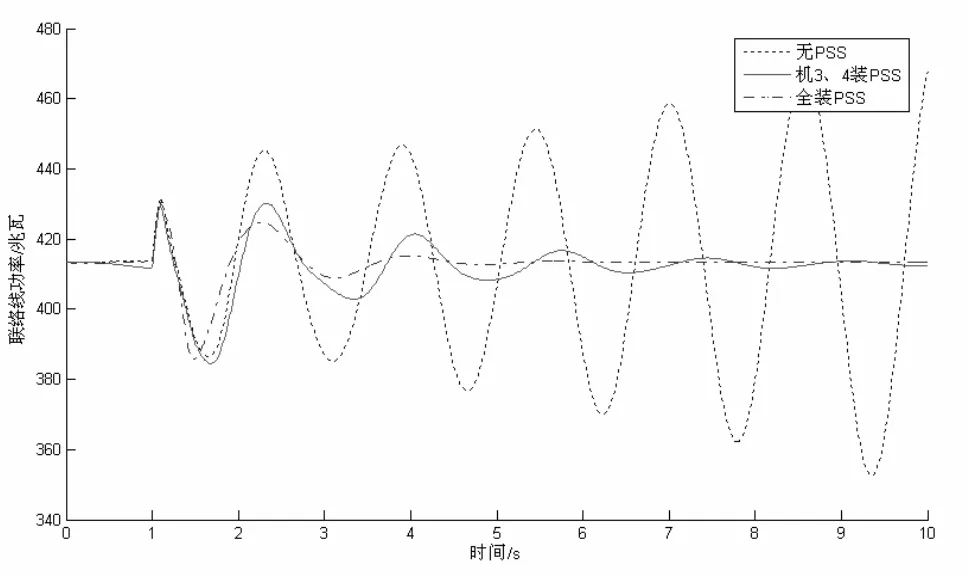
图7 不同PSS配置点下的联络线上功率振荡曲线

4 结论

本文通过基于Matrix Pencil方法的传递函数辨识，并对建立的系统低阶近似传递函数，并与4机2区域系统输出对比，结果验证该方法能准确地得到系统低阶近似传递函数模型；并在此基础上，对系统传递函数基于SVD分解方法分析了多机系统PSS优化配置，并实验仿真分析结果说明基于SVD分解方法的多机系统PSS优化配置是可行有效的。

[1]王宇静,于继来. 电力系统振荡模态的矩阵束辨识法[J]. 中国电机工程学报,2007, 27(19): 12-17.

[2]陈刚,程林,孙元章,张放.采用相量测量单元实测扰动数据的电力系统稳定器参数设计[J]. 高电压技术.2011, 37(3):694-699.

[3]孙勇.电力系统附加阻尼控制器的优化配置与设计方法研究[D]. 哈尔滨:哈尔滨工业大学电气工程系, 2009.

[4]DE MELLO F P, NOLAN P J, LASKOWSKI T F, et al.Coordinated application of stabilizers in Multimachine power system[J]. IEEE Trans on PAS, 1980,99 (3):892-901.

[5]HSU Y Y, CHEN CL. Identification of optimum location for stabilizer applications using participation factors [J]. IEEE Proc on Gener, Trans & Distrib 1987,134 (3):238-244.

[6]PAGOLA F L, PEREZ-ARRIAGE I J, VERGHESE G C. On sensitivities, residues and participations:application to oscillatory stability analysis and control[J]. IEEE Trans on Power System, 1989, 4(1):278-285.

[7]MARTINS N, LIMA L T G. Determination of suitable locations for power system stabilizers and static VAR compensators for damping elector mechanical oscillation in large power system [J]. IEEE Trans on Power System, 1990, 5 (4):1455-1469.