传感器网络时间差双曲线目标定位方法＊

程远国 陈 云 杨津骁

（海军工程大学电子工程学院 武汉 430033）

无线传感器网络（wireless sensor networks，WSN）自组织、自适应和高冗余设计等特性使得其特别适用于目标的定位与跟踪［1］，而对目标的准确定位是目标跟踪的前提.与传统的传感器（如雷达等）相比，WSN节点的软硬件资源有限，要求运行其上的定位算法计算简单、时间和空间复杂度低.目前目标定位方法主要有基于信号到达不同节点的时间的 TOA（time of arrival）方法［2］、基于信号到达不同节点的角度的DOA（direction of arrival）方法［3］、基于信号到达不同节点的时间差的 TDOA（time difference of arrival）方法［4－5］.TOA方法定位精度高，但算法对时间同步要求较高，对节点的硬件和功耗的要求较高.DOA方法易受外界环境影响，且需要额外硬件，在硬件尺寸和功耗上不适用于大规模的WSN应用.TDOA方法具有较高的定位精度，且降低了时间同步的要求，不失为一种可行的WSN目标定位方法.本文采用一种基于声传感器节点的TDOA目标定位方法，目标发出声信号，多个节点接收信号后，估计出信号到达的时间差TDOA，一个TDOA估计值对应的是2个传感器节点为焦点的一对双曲线，多个TDOA估计值对应多条双曲线，这些双曲线的交点即为被测信号源的位置.针对基于TDOA的目标定位问题，文献［6］提出一种利用两点确定声源曲线、利用三点确定声源范围三角，最后采用质心算法确定目标位置的方法.为简化计算，其用于确定声源曲线的两点位于X轴上且对称分布，这在节点随机部署的WSN中不能得到保证.为提高算法的适应性，本文在文献［6］的基础上，建立绝对与相对坐标系，绝对坐标系指的是传感器网络所在区域的地理坐标，依靠节点自定位技术，每个节点能确定自己的位置.相对坐标系指的是在具体定位过程中，数量有限的几个传感器之间建立的局部坐标系.首先选择2点建立相对坐标系X轴，为进一步简化计算，选择位于Y轴上的第三点确定声源范围三角.对目标的定位，是在各传感器节点已经知道自身绝对或相对坐标的基础上开始的.在进行定位时，需要在相对坐标系中计算出目标位置后，再转换到绝对坐标系，最终确定目标的位置.

1 定位方法

1.1 根据2点确定目标曲线

为简化计算，选择2个节点S1，S2建立X轴，见图1.目标T在t时刻发出声信号，在t时刻后，节点S1，S2会相继收到目标传来的信号.

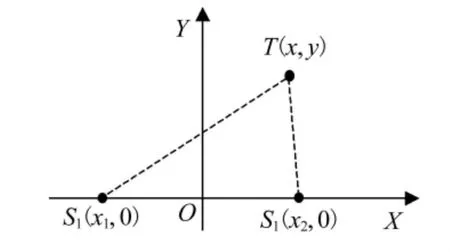
图1 两个传感器确定目标位置曲线

声信号传播速度设为v，信号到达2个传感器网络节点S1，S2的时间差为Δt，则目标T到2个节点的距离之差Δd为

则目标的位置坐标就在这条双曲线上.

1.2 根据3点确定目标坐标

1.1 中，已经用2个已知位置坐标的传感器确定了目标的坐标曲线，如果再建立一个范围，那么这2个范围的交集就是该目标t时刻的位置.如图2所示，增加一个无线传感器网络节点S3（0，y1）.

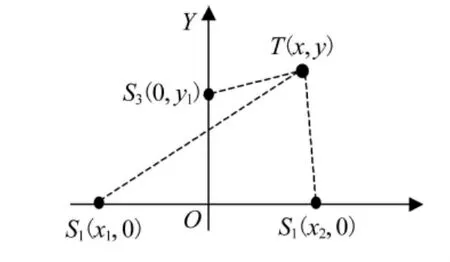
图2 三点确定目标坐标

t时刻目标的信号在之后的不同时刻分别被节点S1，S2，S3收到，在每2个节点之间都产生了距离差值，分别记为ΔdS1S2，ΔdS1S3，ΔdS2S3对应的3条双曲线分别为

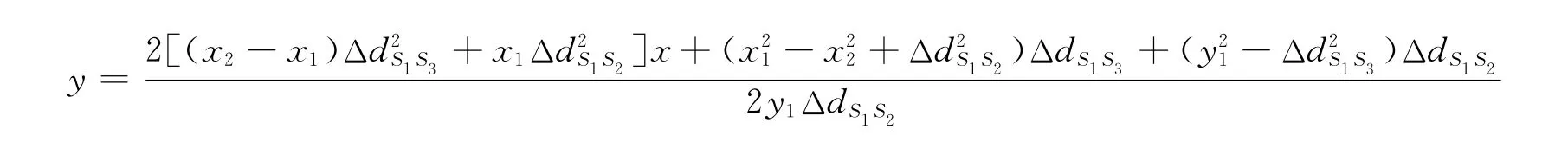
在取定坐标和距离差参数时，要满足B2－4AC≥0，才能使得方程有解.所以根据到达时间差的正负，舍去负根之后有

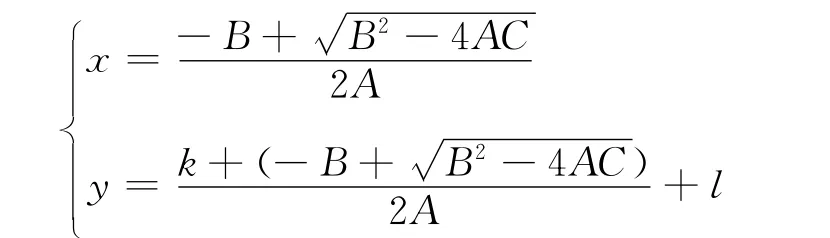
同理，可求得另外2个交点.理想情况下式（4）～（6）会交于一点，该点即为目标位置，但由于存在时间差测量误差等误差，距离差双曲线不会相交于一点，而是两两相交形成三角形.这时可采用质心算法来近似估计目标所在的位置（x，y）.

1.3 坐标转换

在相对坐标系中解算出的目标位置需要转换到绝对坐标系中，见图3.XOY是由传感器节点S1，S2，S3所确定的相对坐标系，而 X′O′Y′是整个传感器网络所在区域的绝对坐标系.其中，S1，S2，S33点的绝对坐标分别设为（xS1，yS1），（xS2，yS2），（xS3，yS3）相对坐标系原点O 的绝对坐标为（xO，yO），α是相对坐标与绝对坐标X 轴之间的夹角.

图3 绝对与相对坐标转换

坐标转换可分为旋转和平移两个步骤.先将相对坐标系以O点为中心旋转成坐标轴与绝对坐标系轴平行的坐标系，这里利用极坐标方程.相对坐标系的极坐标方程为

设旋转后得到的坐标系极坐标方程为

由式（7）、（8）可得

平移时需要首先利用S1或S2，S33点的绝对坐标（xS1，yS1）或（xS2，yS2）、（xS3，yS3），求解出O的绝对坐标，由图3可得

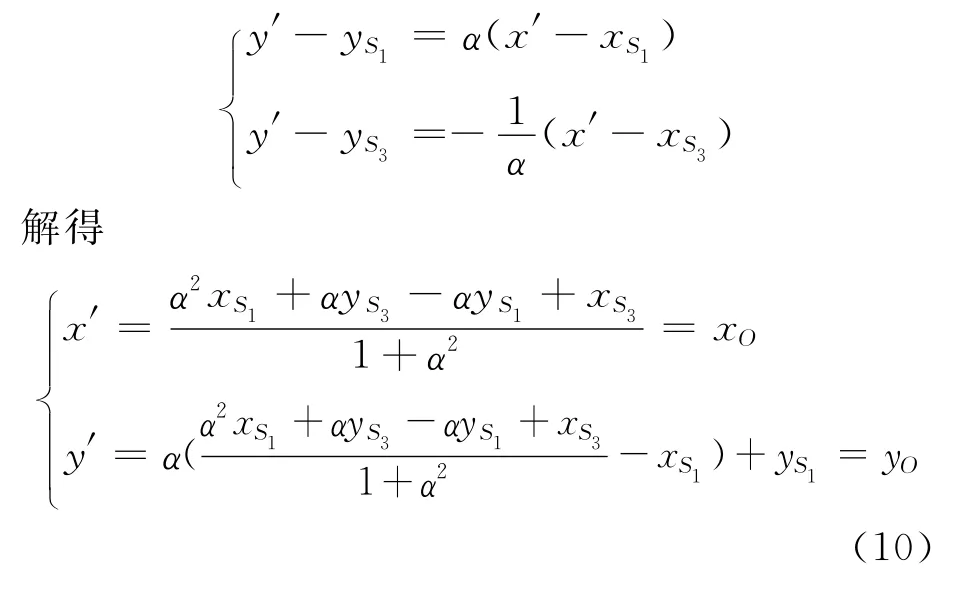
由式（8）和（10），就可以计算出目标T在绝对坐标系X′O′Y′下的坐标为

2 仿真分析

在Matlab中对上述坐标解算进行了模拟，传感器监测区域为1 000×1 000（平方单位），分成121个小方格，121个带有声传感器的节点部署在这些小方格的顶点，传感器通信模型采用文献［7］中的概率0.9模型，通信半径为100长度单位.坐标原点位于左边界中点，目标运动轨迹为正弦函数曲线y＝400sin（π／500vt），速度v0＝50长度单位／s.波速vS为340长度单位／s，按照图1～2原则选取3个传感器节点来计算目标位置，目标到第i（i＝1，2，3）个节点的时间差按照Si／vS计算，其中Si为目标到第i个节点的欧氏距离.分别计算t取20以内整数目标的真实位置和计算位置，见图4.

图4 标解算位置与真实位置

从图4可以看出，目标解算位置与真实位置的误差较小，定位效果较好.

3 结 论

本文根据声信号到达不同传感器时所形成的一组时差，经过解算确定目标位置.为简化计算，选取了位于相对坐标系坐标轴上的3个特殊的传感器节点来生成各自的声源双曲线，计算目标在相对坐标系中的位置，再通过坐标转换，得到目标的绝对坐标系位置，从而实现目标定位.简单的数值仿真表明，这种方法具有较好的定位精度.然而，需要建立更贴近实际的节点能耗和通信模型，设置较复杂的定位场景，进行进一步模拟仿真以评估算法在实时和能耗等方面的性能.

［1］王 伟.无线传感器网络若干关键技术研究［D］.武汉：华中科技大学，2011.

［2］HARTER A，HOPPER A，STEGGLES P，et al.The anatomy of a context－aware application［C］／／Proceedings of the 5th Annual ACM／IEEE International Conference on Mobile Computing and Networking，Seattle：ACM Press，1999：59－68.

［3］BULUSU N，HEIDEMANN J，ESTRIN D.GPS－Less low cost outdoor localization for very small devices［J］.IEEE Personal Communications，2000，7（5）：28－34.

［4］PRIYANTHA N，CHAKRABORTHY A，BALAKRISHNAN H.The cricket location－support system ［C］／／Proceedings of International Conference on Mobile Computing and Networking （MobiCom2000），Seattle：ACM Press，2000：32－43.

［5］陈维克，李文锋，首 珩，等.基于RSSI的无线传感器网络加权质心定位算法［J］.武汉理工大学学报：交通科学与工程版，2006，30（2）：265－268.

［6］张丽霞，汪文勇，李 炯.无线传感器网络的目标定位问题研究［J］.电子科技大学学报，2006，35（2）：239－241.

［7］周红波.无线传感器网络的目标跟踪算法研究［D］.武汉：海军工程大学，2011.