散货船极限强度的标准化非线性有限元分析＊

刘 斌 吴卫国

（武汉理工大学交通学院1） 武汉 430063） （高速船舶工程教育部重点实验室2） 武汉 430063）

0 引 言

船体结构传统的安全设计标准总是以满足船体强度下的最小剖面模数为依据，同时考核船体的局部强度.这些指标都是基于经典的线弹性理论，没有真正地估算出船体达到崩溃的承载能力，很难确定结构真实的安全性.所以，研究散货船的极限强度，并对其进行极限强度分析是相当必要的.这对评估船体结构的真正安全余量，对充分合理利用材料、减轻船体结构重量、增加装载能力，从而提高船舶的经济性都具有重要的实用价值.如今，船体结构极限承载能力作为反映船舶安全可靠的重要指标，已成为船舶界关注和研究的热点问题.相应试验及仿真已经证明了运用大型非线性有限元软件进行极限强度计算的有效性［1－3］.

1 船体概述

该船为国内航行散货船，入级中国船级社（CCS），所装载的货物以煤为主，亦可载运性质类似的其他散装固体干货.主体具有双层底、完整的连续上甲板，采用普通钢、AH32高强度钢和AH36高强度钢.全船共设5个货舱，货舱区域均设计成双舷侧并有底边舱和顶边舱的双壳体结构.肋骨间距从船尾至Fr.11和从Fr.209至船首为600mm，Fr.11至Fr.209为800mm.

表1 船体主尺度 m

2 舱段结构静强度分析

2.1 总括

根据文献［4］规定，运用MSC.Nastran有限元软件对散装货船主要构件进行强度直接计算，为了减少边界条件的影响，模型范围选取货舱区的1／2个第2货舱＋1个第3货舱＋1／2第4个货舱，纵向从Fr.88到Fr.160，垂向范围为船体型深整个舱段有限元模型共有14 467个节点，16 460个板单元，11 426个梁单元.由于舱段结构和计算载荷对称于中纵剖面，因此舱段模型仅取左舷.计算模型见图1.

2.2 边界条件

根据文献［4］在Fr.88剖面（A剖面）和Fr.160剖面（B剖面）中和轴处分别建立刚性点A，B，在刚性点上施加弯矩.舱段模型边界条件见表2.

2.3 计算工况及载荷

根据文献［4］及实际装载情况，选取LC01满载工况进行计算.最大吃水时，货舱装载满货，压载舱为空舱，见表3.

图1 舱段有限元模型

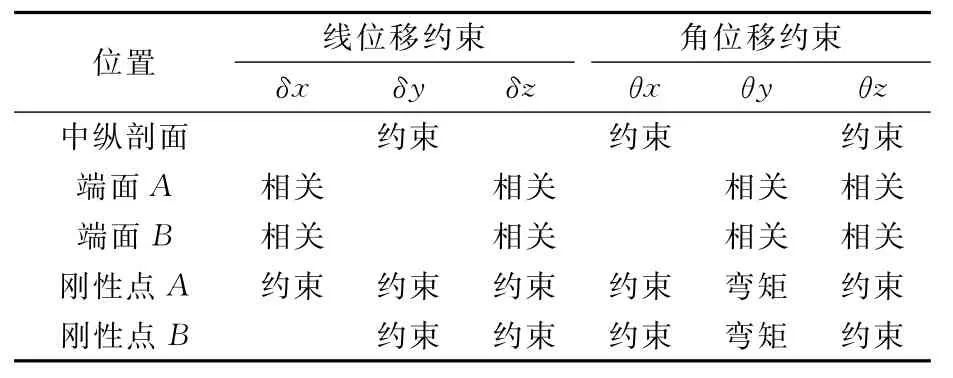
表2 边界条件施加表（载荷对称边界）

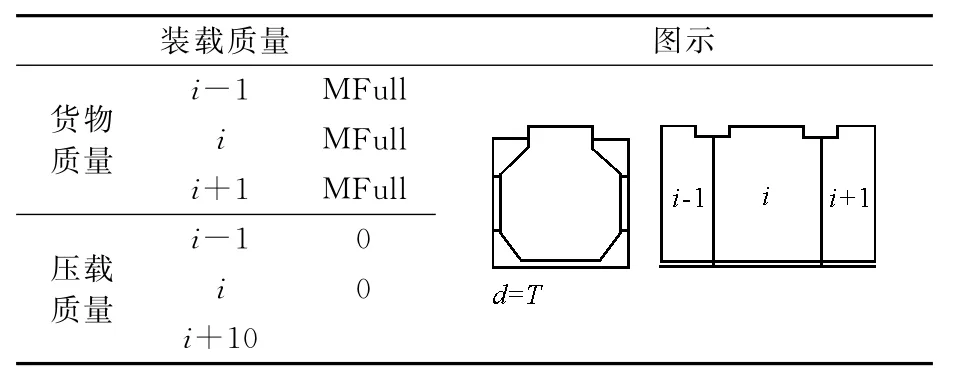
表3 计算载荷工况

Ms和Mw分别为静水和波浪弯矩，中拱为正.舱内货物压力，舷外水压力和端面弯矩，端面弯矩由静水弯矩Ms、波浪弯矩Mw和修正弯矩Mr3部分组成：

根据文献［4］给出的计算公式，由于舱段模型仅取左舷，加载时只取端面弯矩的一半：

2.4 有限元计算结果及分析

根据文献［4］，强度评估采用中间一个货舱（含舱壁）的结果.考虑舷外水压力、舱内货物和压载水压力等情况进行了数值计算，各构件在LC01满载工况下的最大计算von Mises应力汇总见表4，计算结果显示，模型各构件单元的最大相当应力满足规范要求，图2为中间舱段的von Mises应力云图.通过MSC.Nastran进行舱段有限元静强度计算，舱段模型最大von Mises应力为232 MPa.

由于高应力区的受力构件都为高强度钢，当最大von Mises应力达到355MPa时，视为结构出现初始屈服，则该模型屈服所需载荷为1.603 5×106kN·m.但是，运用线弹性理论进行应力分析得到的结果，不能真实评估船舶的极限强度，需要进一步同时考虑到船体结构的非线性——材料非线性（屈服和塑性变形）和几何非线性（屈曲和大挠度）.因此，下面对舱段模型进行极限强度非线性有限元分析，得到结构的极限承载能力.

图2 舱段von Mises应力云图

表4 货舱区主要构件应力情况 N·mm－2

3 舱段结构极限强度分析

3.1 总括

运用MSC.Marc非线性有限元法对该散货船进行极限强度分析，计算模型与上述模型相同，考虑材料和几何的非线性因素.该散货船采用普通钢、AH32高强度钢、AH36高强度钢3种钢材.运用Riks－Ramm弧长法和全Newton－Raphson迭代方法来分析有限元模型，考虑大变形，有限应变和跟随力，材料定义为理想弹塑性材料，使用屈服应力分别为235，315和355MPa的3种理想弹塑性材料，弹性模量为210GPa，泊松比为0.3.

3.2 边界条件及载荷

约束条件和上述模型相同.LC01满载工况为初始载荷，通过不断增加端面弯矩，来计算舱段的极限强度.

3.3 非线性有限元计算结果与分析

通过非线性有限元计算，设置适当的步长及收敛准则，得出下列结果.图3为舱段有限元模型在极限载荷作用下的von Mises应力云图.图4为舱段有限元模型的弯矩－变形曲线.从图4可以看出，对应于它的极限弯矩加载系数是0.755 0，则

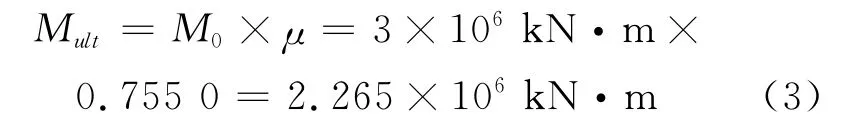
式中：Mult为舱段有限元模型的极限弯矩；M0为施加端面弯矩；μ为极限加载系数.

图3 舱段在极限载荷下的应力云图

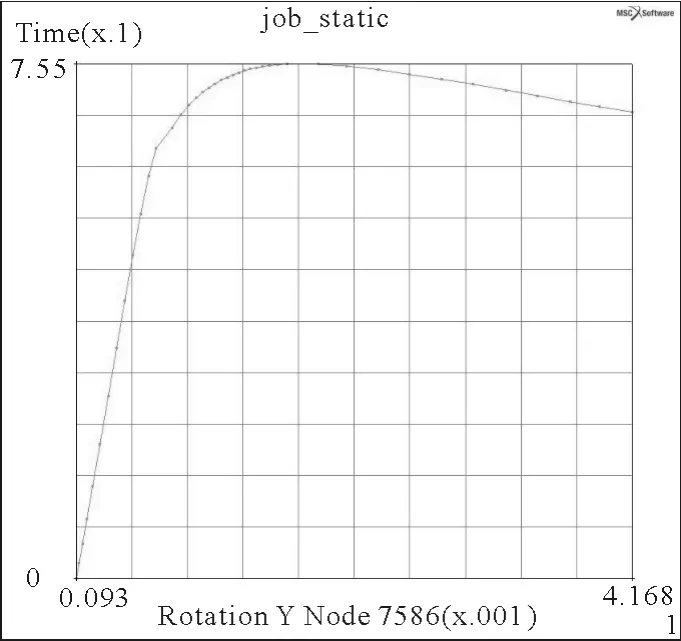
图4 舱段的弯矩－变形曲线

基于线弹性应力计算的有限元分析没有考核船体的真正极限承载能力.在船体结构强度计算中，非线性有限元分析能够确定船体真实的极限弯曲强度，即最大抵抗外加荷载的能力.在这个基础上，最终可以确定船体极限承载能力与最大期望弯曲能力之间的真实安全余量.极限强度是初始屈服强度的1.413倍.由于散货船的工况太多，加载太复杂，通过一算例仅加载端面弯矩，对散货船舱段进行极限强度计算.图5为舱段有限元模型在极限载荷作用下的von Mises应力云图.图6为舱段有限元模型的弯矩－变形曲线.从图6可以看出，对应于它的极限弯矩加载系数是0.752 2，则

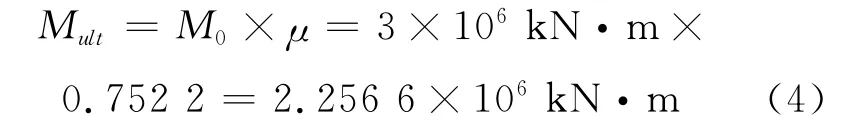
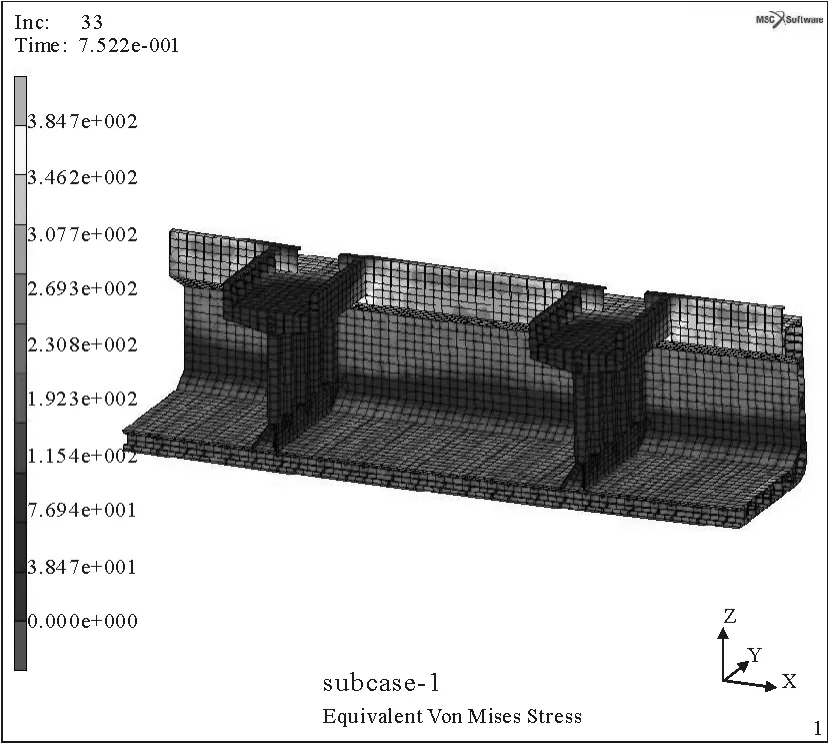
图5 舱段在极限载荷下的应力云图（简化工况）

图6 舱段的弯矩－变形曲线（简化工况）

两个计算结果非常接近，由此可见，只加载端面弯矩计算散货船极限强度，同样能够达到精度要求.这种方法简化了模型的加载，节省了工作量，便于极限强度计算的标准化.

4 结束语

运用同一个模型进行计算，可以实现运用以结构极限强度为基础的非线性设计与以结构静强度为基础的线弹性设计相结合的方法进行船体结构设计.进行散货船结构设计时，考虑腐蚀及破损后的强度，结构强度都留有很大的余量.通过船体极限强度计算，可以得到船体真实的安全余量.进行舱段极限强度分析时，只需考核端面极限弯矩，而不需根据各种工况进行加载.

［1］LIU Bin，WU Weiguo，HUANG Yanling.Ultimate strength test study of SWATH ships［C］∥Proceedings of International Offshore and Polar Engineering Conference，Osaka，Japan，June，2009：114－121.

［2］LIU Bin，WU Weiguo.Study on ultimate strength analysis method for SWATH ships［C］∥Proceedings of International Conference on Ocean，Offshore and Arctic Engineering，Honolulu，Hawaii，May，2009：1021－1029.

［3］SUN Haihong，GUEDES S C.An experimental study of ultimate torsional strength of a ship－type hull girder with a large deck opening［J］.Marine Structures，2003（16）：51－67.

［4］中国船级社.双舷侧散货船结构强度直接计算指南［M］.北京：人民交通出版社，2004.