基于实测数据的路段可靠性近似算法研究＊

高爱霞 陈艳艳

（北京警察学院治安系1） 北京 102202） （北京工业大学交通工程北京市重点实验室2） 北京 100022）

在路网中没有异常事件发生的情况下，交通系统的随机性主要由交通流量［1－3］的变化导致的，因此常态下，对于确定的路网而言，其可靠性主要是由交通流量及其变化决定.本文利用实测数据分析交通流量的变化规律，研究在流量波动范围固定的情况下，饱和度与可靠度之间的关系，从而简化可靠度的计算，使该指标更方便的应用于交通管理和规划.

1 交通流量的变化规律分析

为了分析典型时段的流量分布特征，选择高峰时段为分析对象.分析所用数据是北京市2011年4月～6月期间利用视频检测设备采集得到的快速路和主干路流量数据，共计90d.首先对2011年4月～6月不同月份工作日的早高峰时段路段流量的概率分布进行拟合.其中，工作日选取周一至周五的数据，早高峰时段设为07：00～09：00，选择每个工作日的最大15min高峰交通量换算为相应的高峰小时流率，然后进行采集时间内的同一高峰时段的流量分布检验，交通流量概率分布拟合和检验的基本步骤如下.

步骤1 进行数据预处理，研究常态下的交通流量的变化规律，须剔出异常情况下的流量数据，需对数据进行质量控制.

步骤2 选择路段流量作为数据样本，对该数据样本做频数分析，勾画流量的直方图，对流量的概率分布征进行初步分析.

步骤3 进行正态分布的Kolmogorov－Smimov检验（K－S检验）［4］.K－S检验可以检验样本数据是否服从指定的正态分布.K－S检验的结果用统计量D对应显著性水平来判断.若相伴概率p值大于指定的显著性水平（通常取0.05），则接受本数据服从正态分布的零假设；如果小于指定的显著性水平，则拒绝假设.

对快速路、主干路早高峰时段的流量数据概率分布进行曲线拟合，结果见图1～6.

图1 西直门－积水潭

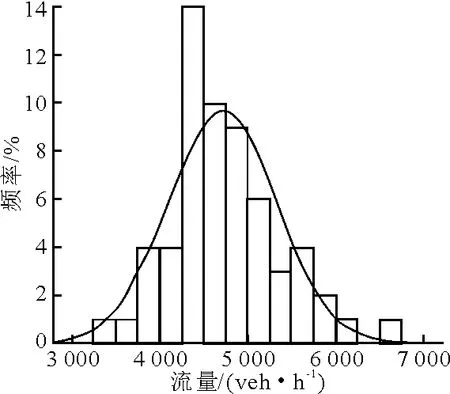
图2 积水潭－西直门

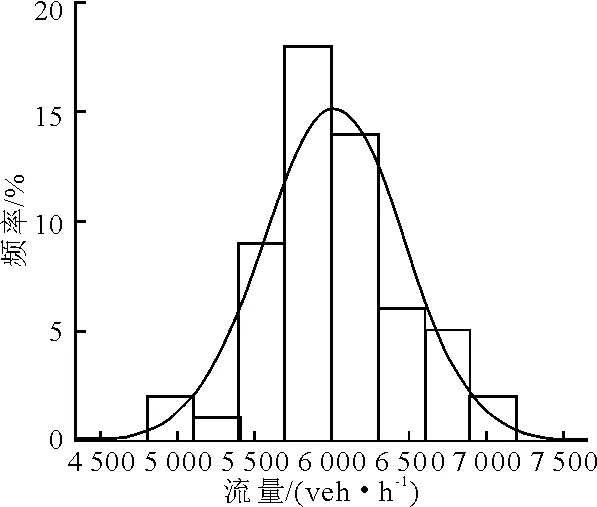
图3 联想桥－四通桥

图4 四通桥－联想桥

图5 地铁路

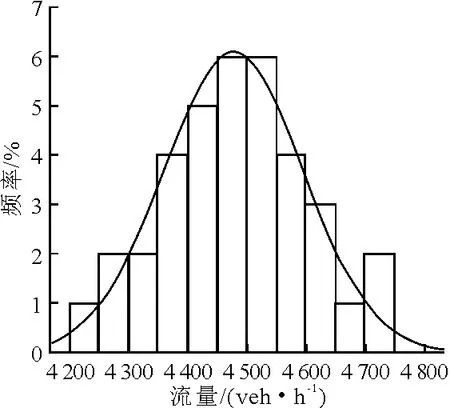
图6 平安大街

K－S检验结果见表1.

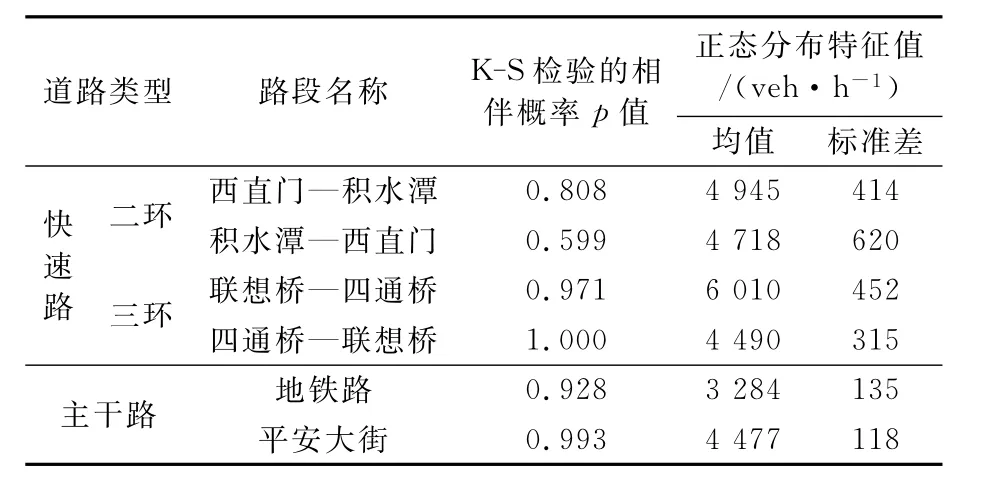
表1 不同等级路段高峰小时流量正态分布检验结果及特征值

由表1可见，6条路段的p值均大于0.05，则6条路段均通过“交通流量服从正态分布”的K－S检验.因此，可以假设快速路和主干路交通流量的概率分布为正态分布.

2 速度－流量关系分析

本文利用速度参数计算可靠度，为了确定可靠度与饱和度之间的关系模型，首先寻找速度－流量关系.根据统计数据，绘制速度－流量散点图，见图7.

图7 快速路流量－速度散点图

图8 主干路流量－速度散点图

从实测数据的速度－流量散点图7、图8可以看出：速度－流量散点的分布形式呈抛物线状，这与 Greenshields所指出的速度－流量曲线［5－6］形状基本相同，但是在阻塞流阶段，当流量趋于零时，速度值并不是趋于零.用spss统计分析软件拟合速度－流量关系曲线，通过数据拟合得出了快速路与主干道速度－流量曲线模型的参数值范围、检验判定系数和曲线模型形式见表2.模型的检验判定系数R2达到了0.85以上，这说明曲线的拟合效果是比较好的.

表2 速度－流量关系曲线拟合模型

3 饱和度及流量波动与可靠性的关系研究

根据交通流量的正态分布特性以及流量－速度的关系模型，可以计算在交通流量波动范围（流量标准差与其均值的比值）一定的情况下，每一个平均饱和度值所对应的速度参数，利用此速度参数根据畅通可靠度的计算方法［7］计算对应的可靠度值，从而可以得到平均饱和度与可靠度之间的一一对应值.图9～图11为计算得出的不同流量波动范围内，饱和度与可靠度的对应值.其中可靠度为路网处于基本畅通常态的可靠度［8］，相当于单位距离出行时间阈值为2.0min／km.

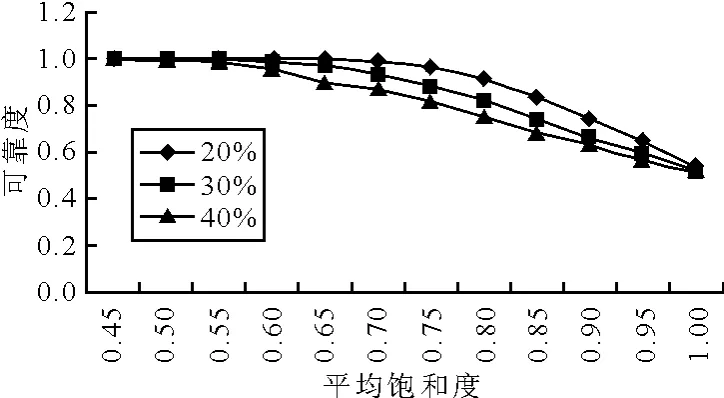
图9 快速路的饱和度（欠饱和）及流量波动与其可靠度的对应值

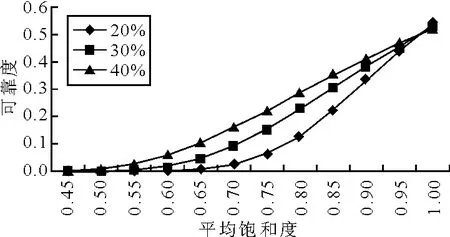
图10 快速路的饱和度（超饱和）及流量波动与其可靠度的对应值

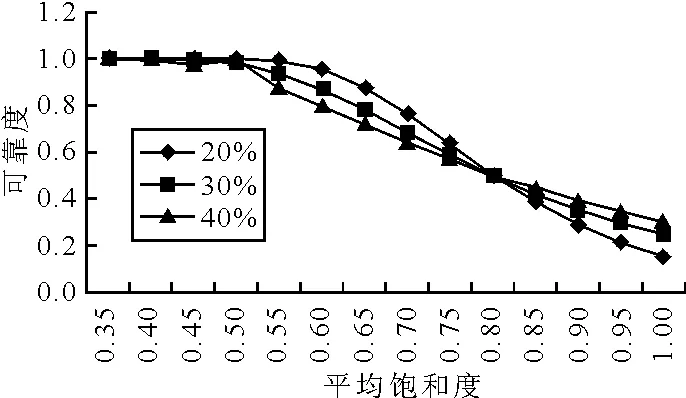
图11 主干路的饱和度（欠饱和）及流量波动与可靠度的对应值

由图9可以见，不同的流量波动，对于同一饱和度，对应的可靠度不同.波动范围越大，可靠性越差.同时在欠饱和的情况下，随着饱和度的升高，可靠度下降，当饱和度趋近于1时，可靠度下降至0.5左右，表明路网处于临近饱和的状态下，可靠性大大降低，有近50%的车辆速度达不到标准畅通速度.由图10可见，当超饱和度达到0.5以下，可靠度接近0，即此刻状态下所有车辆的速度都达不到标准畅通速度.由图11可见，当饱和度接近于1时，可靠度下降至0.2左右，接近80%的车辆车速达不到标准畅通状态.利用spss软件进行曲线回归，得到快速路和主干路的饱和度与可靠度的关系见表3.

表3 快速路、主干路饱和度（S）与可靠度（R）的函数关系

4 模型的验证

根据得到的饱和度与可靠度的函数关系，可以求得快速路与主干路其他路段的可靠性，然后与利用统计法［9］得到的可靠度值（参考值）比较，验证该算法在其他路段的适应性.利用该算法与统计法分别得到的可靠度值见表4.

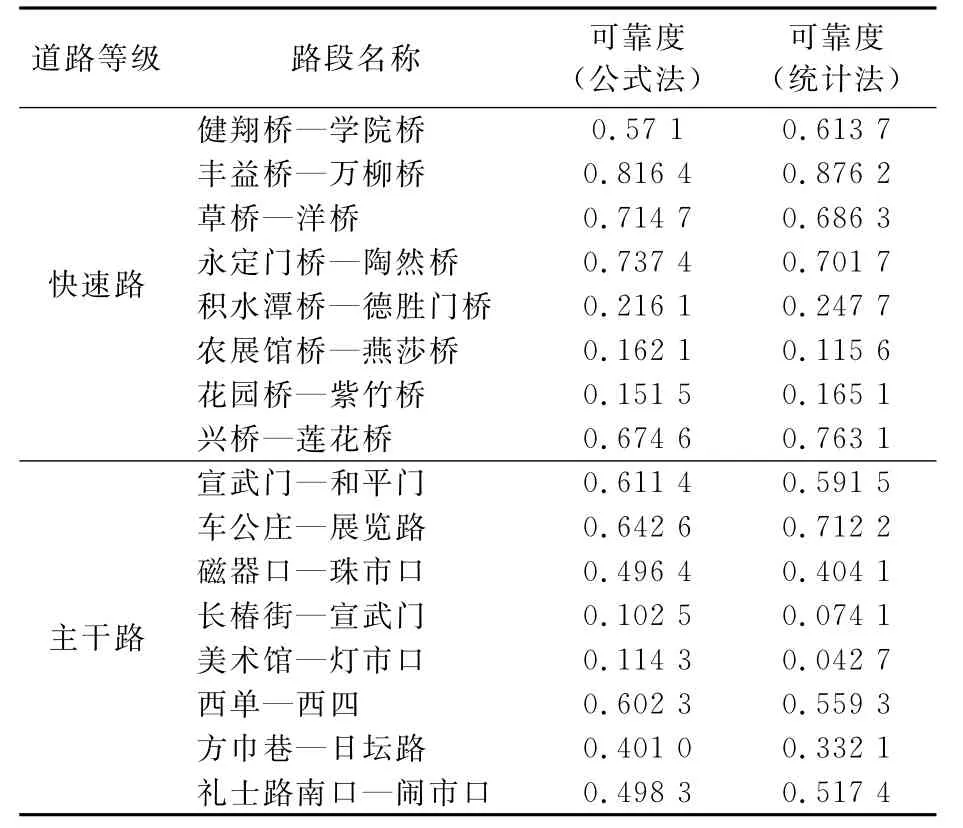
表4 可靠度的计算值与参考值比较

由表4可见，快速路中利用公式法与利用统计法得到的可靠度最大相差0.088 5；在主干路中用不同方法计算得到的可靠度值最大相差0.092 3.这是由于流量－速度模型的标定及饱和度与可靠度的函数关系拟合过程中都有不同程度的近似，导致最终的计算值与实际值会有不同程度的差别.但是最大误差没有超过10% ，因此在可靠度计算中可以采用该方法.

5 结束语

本文提出的算法与以往的算法相比，计算较为简单，已知饱和度和流量波动范围，就可以很容易的获得路段的可靠度值.此方法运用于路网的规划、设计与管理中，可有效地对规划设计方案及管理措施进行可靠性评价，为设计及管理部门决策提供支持.

［1］IIDA Y.Basic concept and future directions of road network reliability analysis［J］.Journal of Advanced Trnsportation，1999，33（2）：125－134.

［2］ASAKURA Y，KASHIWADANI M.Road network reliability caused by daily fluctuation of traffic flow［C］∥19thPTRC Summer Annual Meeting，Proceedings Seminar G，1991：73－84.

［3］高爱霞，陈艳艳.异常事件下路网恢复可靠性研究［J］.武汉理工大学学报：交通科学与工程版，2010，33（2）：517－520.

［4］阮桂海，蔡建平，刘爱玉.数据统计与分析：spss应用教程［M］.北京：北京大学出版社，2005.

［5］高爱霞.城市路网可靠性及其保障技术研究［D］.北京：北京工业大学，2010.

［6］任福田.新编交通工程学导论［M］.北京：中国建筑工业出版社，2011.

［7］陈艳艳，刘小明，梁 颖.可靠度在交通系统规划与管理中的应用［M］.北京：人民交通出版社，2006.

［8］梁 颖.城市交通系统畅通可靠性分析与优化［D］.北京：北京工业大学，2005.

［9］唐茜茹，陈艳艳，段卫静.城市路网畅通可靠度计算方法及其应用［J］.城市交通，2011（1）：40－46.