基于集值统计法在项目评估中的可信性检验

余 彬， 朱永忠

(河海大学理学院，江苏南京211100)

实际生活中，许多项目在实施前需要被客观地评价，然而在整个评价过程中会出现很多不确定性因素。如果评估者在评价时，采用传统的概率统计手段，给出的是一个估计值，用刚性的“点”去描述，往往不能很好地描述事物的真实性［1］。若能用一个模糊地区间去评价它，这样在评价时就能降低评估者在赋值时的主观性［2］。汪培庄教授首次提出了集值统计方法，在概率统计实验中，每次得到的实验结果是象空间的一个模糊子集，称这种实验为集值统计实验［3］。评估过程中的各种不确定因素是集值统计法在评估时的有利因素，它的区间评价很好地满足了评估者的模糊心理。

近年来，集值统计法有了很大发展。一方面集值统计法在教学评估、项目决策、气象预测等不同的领域得到了较好的应用。邢云磊、张喜将集值统计法应用到了大型客运站的风险评估研究上［4］，陈斯、陈岗将其应用到了项目融资上［5］，罗晓芳将其应用到了教学评估上［6］，廖文来、何金平将其应用到大坝安全的监测上［7］。另一方面，对集值统计法的改进也取得了较大进展。一是对评估者给予了不同的权重。孙九春、史家均利用评估者给出的评价区间的相似性与差异性给出专家权重的赋权方法［8］。二是对各项方案中指标权重的改进。钟小伟、傅鸿源［9］和王炜［10］等人采用层次分析法来确定指标的权重［9］，陈骥采用特尔菲法和层次分析法相结合来确定指标的权重［11］。也有人采用专家调查法、判断矩阵法和区间打分法给出指标权重的计算方法。但是传统的集值统计法在对评估结果进行检验时，往往也只是一个模糊的评断标准。例如，当结果的可信度大于90%时，就相信评估结果是可信的。可是在很多情况下，即使这些评估区间中出现一些异常的区间，得到的可信度仍大于90%，这时应该选择哪一个方案呢?没有出现异常区间的方案还是出现了异常区间的方案呢?很显然，传统的集值统计法中的检验方法已经行不通了。

文中在传统的集值统计法基础上，建立了在数据删除模型下的可信性检验，通过对区间的检验，判定出给评估结果带来不利影响的异常区间，根据带来的影响程度的高低，对相应的评估值赋以不同的权重，得到最终的评估结果。结果显示，通过改进后的集值统计法得到的评估结果可信度更高。

1 基于集值统计法的评价模型

假设共有n位评估者，对i项方案进行评估，每位评估者对每项方案给出一个区间估计值，记为位评估者对方案j的评价值可得一个集值统计序到一个评估矩阵，见表 1所示。

表1 评估者给出的评估矩阵Tab.1 Evaluation matrix given by the evaluator

其中，ajk(1≤j≤i，1≤k≤n)表示第k位评估者对第 j个方案所作出的评价值，其

将这n个区间叠加在一起则形成覆盖在评价值轴上的一种分布。这种分布可用下式描述:

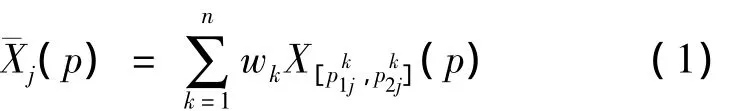
其中，wk是n位评估者的权重，

由式(3)，(4)，(5)得

由式(1)，(3)，(6)，(7)可推得

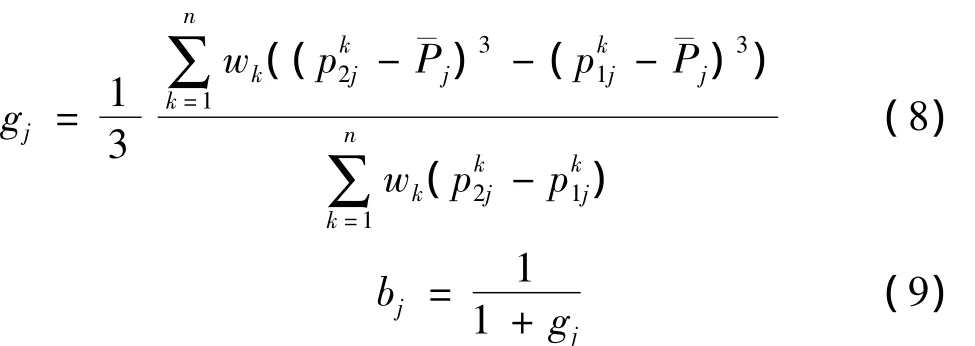
2 传统集值统计法的缺陷

传统的集值统计法在对评价结果进行可信性检验时，往往是根据评价函数得到的b值来判定，当b值大于0.9时，就相信评价结果是可信的。但是，当遇到几项方案的平均成绩相差无几，而评价函数得到的b值又都大于0.9时，又该如何取舍呢?为了方便说明，举出下面例子。

假设现在有4套方案，由5位评估者进行打分，所得到的评估矩阵如表2所示。

由表2可以看出，有一些方案中，并不是每一位评估者给出的评价区间都是相同的，由于评估者的专业性等原因而出现这种差距，是可以理解的。若按孙九春的文章中提到的由评价区间的相异性与差异性求评估者的权重，刚好每一位评估者出现一次异常的评估，为了方便起见，暂且认为每位评估者的权重是相同的。经过计算得到方案1，2明显大于方案3，4，但是到底选择方案1还是方案2，这儿遇到了问题:

方案1的平均估计值和可信度分别为

方案2的平均估计值和可信度分别为

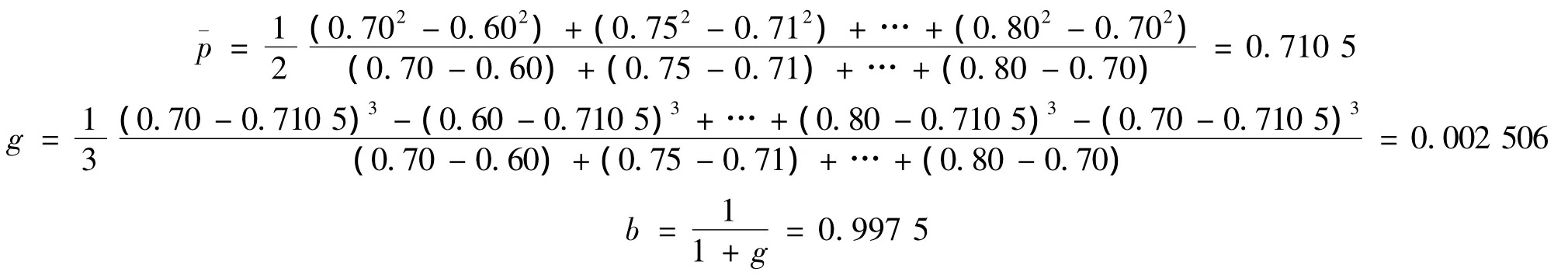
表2 5位评估者对4套方案的评估Tab.2 Four schemes＇evaluation given by the five evaluators

由结果知道，两者的可信程度均在0.99以上，具有很好的可信度，两者的平均值，也相差无几。到底选择哪一个方案，传统的评估准则已经不能很肯定地给出一个令人信服的答案。从这里可以看出，异常区间的出现打乱了传统的评估方法。文中尝试找出一个好的办法，对异常区间进行处理，使评价结果更符合实际情况。

3 数据删除模型下的集值统计可信性检验

数据删除模型是统计诊断的基本模型，比较删除模型与未删除模型相应统计量之间的差异是统计诊断最基本的方法。下面结合集值统计法对评估区间进行检验。

给定一组评估区间集 Z={z1，z2，…，zn}，检验第i个区间zi是否为异常区间。如果区间zi是异常区间，那么删除该区间之后，所得结果的可信度bi值与未删除该区间时的b值相比，将变大;同时得到的值将更趋近真实情况，如果区间的异常程度越高，得到的bi值会越大值越接近真实值。

基于数据删除模型，知道当可信度的变大时，这个时候得到的平均值也更接近真实水平。通过删除模型的检验，已经知道了区间中的异常区间，通过对异常区间Δbi的相对改变量对相应的赋予权重wi，最终的综合评价值

实例分析:为了说明改进后模型的有效性，对上文的两方案用该模型进行检验，得到的结果见表3和表4，b值表示未删除区间时的平均估计值和可信度，bi值表示删除第i个区间zi后的值)。

从表3和表4可以看出，由数据删除模型从可信度的改变量看，方案1的可信度所有区间在删除后都是减小的，而方案2有两个区间在删除后可信度是变大的，即所给区间中有两组是异常区间，第一组和第五组。那么方案2最终结果会有变化，由公式(10)得到改进后的最终综合评价值:

表3 方案1评估区间删除前后的比较Tab.3 Difference of the result after the first scheme's evaluation interval delete

表4 方案2评估区间删除前后的比较Tab.4 Difference of the result after the second scheme's evaluation interval delete

由此可以看出，反而出现了异常区间的方案2得到的最终评价值大于方案1。为了检验方案2最终评价值的可信度，已知在忽略评估者自身权重差异的情况下，即对每位评估者给出的区间赋予相同的权重，那么在删除两组异常区间后得到的综合值是最接近真实值的，删除两组数据后得到的平均值:

4 结语

在评估者对评价指标进行评估时，由于评估者本身和评价对象含有的各种不确定性因素，文中采用集值统计法对指标给出一个区间估计，并针对这些区间出现的异常区间，对这些区间进行处理，处理后发现评价结果的可信性更高，更能反映评估者的真实意图，使评价结果更符合实际情况。通过举例分析，发现当两个方案在均值相同的情况下，并不一定是出现异常区间的方案更差。但值得注意的是，对异常区间的处理过程还比较繁琐，找出一种更简洁的方法将是笔者进一步的研究方向。

［1］宗金峰，赵淑芹.引入集值统计改进德尔菲法中数据处理过程［J］.统计与决策，1997，13(3):10-11.ZONG Jin-feng，ZHAO Shu-qin.Introducing set-valued statistics modified delphi method in the process of data processing［J］.Statistics and Decision，1997，13(3):10-11.(in Chinese)

［2］汪培庄.模糊集与模糊集落影［M］.北京:北京师范大学出版社，1985.

［3］刑云磊，张喜.基于集值统计的大型客运站风险评价研究［J］.铁路计算机应用，2009，19(1):5-6.XING Yun-lei，ZHANG Xi.Study on risk assessment of large passenger station based on set-valued statistical method［J］.Railay Computer Application，2009，19(1):5-6.(in Chinese)

［4］陈斯，陈岗.基于集值统计的项目融资技术方案评价［J］.科技与市场，2009，9(16):64-66.CHEN Si，CHEN Gang.The evaluation of technical scheme of project financing based on set-valued statistics［J］.Technology and Marked，2009，9(16):64-66.(in Chinese)

［5］罗晓芳.基于集值统计的模糊综合评判及其应用［J］.数学的实践与认识，2005，35(9):42-44.LUO Xiao-fang.Fuzzy synthetic evaluation based on set-valued statistics and its application［J］.Mathematic in Practice and Theory，2005，35(9):42-44.(in Chinese)

［6］廖文来，何金平.集值统计法在大坝安全巡查量化分析上的应用［J］.人民长江，2005，36(4):68-71.LIAO Wen-lai，HE Jin-ping.Set-valued statistics in the quantitative analysis of dam safety patrol［J］.Yangtze River，2005，36(4):68-71.(in Chinese)

［7］孙九春，史家均.加权集值统计理论和重心决策理论在桥梁评估中的应用［J］.桥梁工程，2001(4):21-22.SUN Jiu-chun，SHI Jia-jun.Weighted set-valued statistics theory and center of gravity decision theory in the evaluation of bridge［J］.Bridge Construction，2001(4):21-22.(in Chinese)

［8］钟小伟，傅鸿源.基于集值统计的综合评价模型及方法［J］.统计理论与方法，2012，27(4):88-90.ZHONG Xiao-wei，FU Hong-yuan.Interval comprehensive evaluation and its application based on set-valued statistics［J］.Staticstics Information Forum，2012，27(4):88-90.(in Chinese)

［9］陈骥.基于集值统计的科研项目立项评审方法及其应用［J］.科技进步与对策，2011，28(19):29-31.WANG Wei.Research on the synthetic evaluation method grounded on mass statistics to define the profit sharing rate of patent assets［J］.Science and Technology Management Research，2011，28(19):29-31.(in Chinese)

［10］王炜.基于集值统计的专利资产利润分成率综合评价法研究［J］.科技管理研究，2011(11):34-36.CHEN Ji.The evaluation method of research project based on set statistics and its application［J］.Science Technology Progress and Policy，2011(11):34-36.(in Chinese)

［11］陈骥.基于集值统计的科研项目立项评审方法及应用［J］.科技进步与对策，2011，28(19):29-31.CHEN Ji.The evaluation method of research project based on set statistics and its application［J］.Science Technology Progress and Policy，2011，28(19):29-31.(in Chinese)