透空式防波堤在渔船避风港中的综合研究

闫少华， 陈德春*， 马 林

(1.河海大学 港口海岸与近海工程学院，江苏 南京 210098;2.镇江市航道管理处，江苏 镇江212000)

渔港是沿海渔区十分重要的基础设施，21世纪以来超强台风沿我国东海岸线频频登陆，以致渔民生命与财产遭受损失，为使渔港成为沿海防灾减灾体系的有机组成部分，推动渔区经济、社会、文化发展，首要解决渔船在台风期避风和安全锚泊问题［1］。

透空式防波堤属新型结构，具有结构简单、适用软基、堤身下部透空，有利于堤后水域内外水体交换，减少港区泥沙淤积的优点。近20多年来，国内对透空堤建设已有一些研究及工程实践。

麻志雄等［2］以上海吴淞口炮台湾船舶基地高桩承台透空堤工程为例，在风浪水槽中进行透浪系数物理模型试验，得到该透空堤透射波高与水深、波要素、堤宽、挡浪板入水深度的关系。文献［3］给出了透空式防波堤结构与透浪系数Kt的计算公式。陈德春等［4］在威格尔对直板透浪系数研究基础上，采用微幅波理论推导不同间距挡板的透空堤透浪系数计算公式，并基于广东省海安新港荔枝湾防波堤物理模型试验研究，得出透浪系数计算值与规范值及试验值变化趋势是一致的，当挡板入水深度与堤前水深之比(t/d)在0.35～0.50时与规范值吻合相对较好。

浙江省台州市大陈渔港位于大陈岛［5］，其规模较小，无法满足渔船安全避台风的需要。而该岛中咀湾三面环山，西面临海，是一个适合渔船避风的海湾，因地质为深层淤泥，需建设透空式防波堤以形成渔船避台风锚地。

我国透空堤工程实践表明［6-8］，透空堤的透浪系数与工程区域的水深、波浪要素和透空堤结构尺度有关。中咀湾的水深与波要素关系不在规范给出的透浪系数Kt计算公式范围内，文中通过物理模型试验测定拟建中咀湾透空堤断面的透浪系数Kt，确定合理的透空堤挡板入水深度。同时考虑渔船能够进出方便及得到有效的锚地面积，进而研究透空堤透浪系数与合适的建设长度，以达到透空堤整体防浪效果。

1 透空堤断面透浪系数物理模型试验

中咀湾位置示意如图1所示，其透空堤设计断面(见图2)为高桩墩台式结构［5］，堤身两侧设置挡浪板，每榀排架设4根600×600 mm预应力混凝土组合桩，4根桩组成两对斜度为4∶1的叉桩。

图1 中咀湾位置示意Fig.1 Schematic diagram of Zhongzui bay’s location

图2 中咀避风港透空式防波堤断面Fig.2 Sectional drawing of the permeable breakwater in Zhongzui bay fishing boats haven

1.1 水位和波要素

透空堤具有上部结构挡浪，下部过流，减少堤后水域泥沙淤积的优点。为最大限度发挥上部结构消波性能，试验中考虑了极端高水位▽5.71 m、设计高水位▽4.41 m和水位▽2.50 m，3级水位50年一遇波况下，透空堤设计波要素见表1。

表1 透空堤设计波要素Tab.1 Design wave elements of the permeable breakwater

1.2 试验条件和方法

遵循模型相似理论，依重力相似准则进行设计，考虑实验室内波浪水槽尺度与透空堤设计断面尺寸、堤前水深、设计波要素等因素，试验断面取正态模型、比尺为 1 ∶24［9－11］。

分析设计断面(见图2)，透空堤设计断面两侧均设挡浪板，由于挡浪板入水深度对透浪系数的影响较大，因此，试验中研究了透空堤4种挡浪板入水深度方案的消浪效果。

4种挡浪板入水深度分别为:

1)两侧挡浪板入水深度至▽0.9 m;

2)两侧挡浪板入水深度至▽1.1 m;

3)两侧挡浪板入水深度至▽1.3 m;

4)两侧挡浪板入水深度至▽1.5 m。

1.3 各方案透空堤断面波浪透浪系数试验结果

在3级水位与不规则波浪作用下，透空堤不同挡浪板入水深度时透浪系数见表2，其对应的堤后有效波高沿程分布如图3所示。

表2 不规则波作用下透空堤透浪系数Tab.2 Transmission coefficients of the permeable breakwater under the action of irregular waves

图3 不规波作用下透空堤堤后有效波高沿程分布Fig.3 Significant wave height distributions along the path after the permeable breakwater under the action of irregular waves

分析透空堤断面透浪系数试验结果表明:

1)水位对透浪系数的影响。随水位自极端高水位▽5.71 m下降到▽2.50 m水位时，透浪系数逐渐增大。

2)挡浪板入水深度对透浪系数的的影响。由于挡浪板入水深度对入射波浪的阻挡作用，穿过透空堤断面的堤后波高已明显发生改变，相同水位波浪条件下，挡浪板入水深度增大，堤后波高值减小，透浪系数下降，消浪效果增强。

3)透空堤后纵向有效波高分布。由于渔船功率一般在448 kW以内，确保其锚泊安全的抗浪性能控制指标为有效波高Hs≤1.0 m。经透空堤挡潮消浪后，堤后最大波高位于透空堤后5 m处，堤后纵向120 m范围内有效波高值是沿程减小，且小于1.0 m。

1.4 透空堤断面推荐方案

透空堤挡浪板不同入水深度对透浪系数的影响较为明显，挡浪板入水深度大，消浪效果好。但是，随着挡浪板入水深度增大，外侧波浪近似于立波，波浪水平作用力也随之增大，不利于堤身自身安全;同时，挡浪板入水深度增大，也会影响透空堤下部过流，增大湾内淤积。因此，文中推荐方案3为透空堤设计断面，即挡浪板低高程(入水深度)定为▽1.3 m。

2 透空堤整体防浪掩护数值计算

透空堤整体防浪掩护效果以最不利水位时，堤后水域有效波高Hs≤1.0 m面积最大为参考。当波浪传入湾内时，一种方式是波浪透射穿过堤身进入(以透浪系数判断)，另一种方式是波浪经过透空堤堤头绕射进入，湾内波浪由这两部分叠加。为确定合适的渔船进出口门宽度、透空堤建设长度，堤后水域满足渔船安全锚泊的面积范围，需采用MIKE 21 BW模块进行透空堤整体防浪掩护效果数值计算。

2.1 MIKE 21 BW的基本方程

MIKE 21 BW 基于 Madsen 和 Sorensen［12］提出的改进的Boussinesq方程数值解，包括两个模式:2DH BW波浪模块和1DH BW波浪模块。其中，2DH BW模式用于计算波浪在港口以及海岸地区的分布情况。

2DH BW波浪模块求解Boussinesq改进方程中的自由水面高程ξ、沿深度积分的速度分量P和Q。Boussinesq方程为

连续性方程:

x方向动量方程:

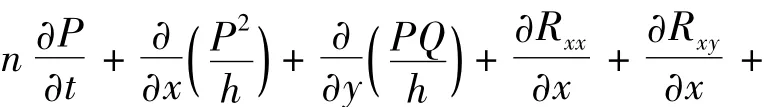
y方向动量方程:

式中:ψ1，ψ2为Boussinesq项;P为x方向的流密度;Q为y方向的流密度;Fx为x方向的水平力;Fy为y方向的水平力;h为总水深;n为孔隙率;C为谢才系数;α为层流阻尼系数;β为紊流阻尼系数。

2.2 模型计算参数设置

选择W和WSW两个对防浪掩护影响较大的波浪来波方向进行数值计算，由于透空堤模型设置的关键参数是透浪系数，由波浪水槽测定的透空堤透浪系数是来波与透空堤断面正交条件下的结果，也是最不利条件下的透浪系数。再根据推荐设计断面尺寸，计算透空部分所占整个断面面积的比率。透空堤的透浪系数见表3。

表3 透空堤的透浪系数Tab.3 Transmission coefficient of the permeable breakwater

2.3 防波堤口门大小的数值模拟

《渔港总体设计规范》［13］要求防波堤口门有效宽度为船长的1.0～1.5倍，由于中咀湾口天然宽度为296 m，考虑渔船的进出安全，数值计算分别研究了口门宽度120 m、透空堤堤长176 m;口门宽度100 m、透空堤堤长196 m;口门宽度80 m、透空堤长216 m 3种不同口门宽度的透空堤防浪掩护效果，并选择最不利水位5.71 m与波高变化比较显著并且可以传到中咀湾湾顶的W波向和WSW波向进行数值计算。为比较锚泊面积范围，在港内设置25个点位采集波高，分析不同方案时透空堤整体防浪掩护效果，湾内水域测波点布置如图4所示，不同来波方向与不同口门宽度时堤后水域波高分布如图5～图7所示，表4为不同口门宽度对应的港内锚泊面积。

图7 极端高水位下，不同方向的港内波高柱形图Fig.7 Columnar diagram of the wave height with extreme high water level and different wave direction

表4 不同口门宽度时港内锚泊面积Tab.4 Mooring area under different widths of the permeable breakwater’s entrance

2.4 结果分析

分析不同来波方向与不同口门宽度时堤后水域波高分布，不同口门宽度时港内锚泊面积，可知:

1)港湾内W方向除了个别点外(有浅滩等原因导致的波能集中)，绝大部分点的波高随着口门宽度的减小而减少，从模拟的波高数据分析可知口门宽度减小对W方向的波高起着显著的阻止作用;另从泊稳面积上看，随着口门宽度的减少，W方向港域内泊稳面积也相应地增加(见表4)。

2)从WSW方向柱形图上可以看出，在口门处1，2，3点随着口门宽度的减小，波高反而增大。这是由于防波堤长度的改变，口门入口处防波堤波能集中后移，使得入口处波高不降而增。但是港湾后面的点的波高基本上都是随着口门宽度的减小而减小的，并且泊稳面积和泊稳面积百分比也符合口门宽度越小泊稳面积越大的规律(见表4)。

综上所述，两个波向在港湾内波高值基本上均随着口门宽度的减小而减小，泊稳面积随着口门宽度的减少而增大。为保证渔船进出安全，推荐口门宽度取100 m。

3 结语

分析波浪断面物理模型试验与整体防浪掩护数值计算结果，得到:

1)透浪系数随水位下降逐渐增大。

2)相同水位、波浪条件下，挡浪板入水深度增大，堤后波高值减小，透浪系数下降。

3)随着防波堤建设长度增加、口门宽度减小，湾内有效波高Hs≤1.0 m泊稳面积增加。

［1］浙江省海洋与渔业局.浙江省沿海标准渔港布局与建设规划［R］.杭州:浙江省海洋与渔业局海洋利用规划处，2007.

［2］麻志雄.透空式防波堤消波性能试验研究［J］.水运工程，1990，10(28):3-8.MA Zhi-xiong.Test and study on the effects of wave dissipation for a permeable breakwater［J］.Port and Waterway Engineering，1990，10(28):3-8.(in Chinese)

［3］交通部第一航务工程勘察设计院.JTJ 298-98防波堤设计与施工规范［S］.北京:人民交通出版社，1998.

［4］陈德春，茆福文，沈丽宁，等.桩基挡板式透空堤透浪系数计算及试验研究［J］.水利水运工程学报，2012(5):83-87.CHEN De-chun，MAO Fu-wen，SHEN Li-ning，et al.Calculation of wave transmission coefficient and experimental study of a permeable breakwater on pile foundation［J］.Port and Waterway Engineering，2012(5):83-87.(in Chinese)

［5］陈德春.台州市椒江中咀避风港防波堤断面波浪模型试验［R］.南京:河海大学，2008.

［6］陈德春.浙江省舟山市定海区西码头渔港扩建工程初步设计总报告［R］.南京:河海大学，2003.

［7］陈德春.洪泽湖16号避风港工程透空堤试验研究［R］.南京:河海大学，2003.

［8］陈德春.广东省海安新港荔枝湾码头一期工程透空式防波堤断面波浪试验研究［R］.南京:河海大学，2004.

［9］南京水利科学研究院.JTJ/T 234-2001波浪模型试验规程［S］.北京:人民交通出版社，2001.

［10］交通部第一航务工程勘察设计院.JTJ 213-98海港水文规范［S］.北京:人民交通出版社，1998.

［11］杨春平.近岸波浪传播变形数值计算方法比较［D］.南京:河海大学，2007.

［12］Madsen P A，Sφrensen O R.A new form of the Boussinesq equations with improved linear dispersion characteristics，part 2:a slowly-varying bathymetry［J］.Coastal Engineering，1992，18(3-4):183-204.

［13］中国水产科学研究院.SC/T 9010-2000渔港总体设计规范［S］.北京:中国标准出版社，2001.