基于人工免疫算法的污水处理系统节能优化*

许玉格 宋亚龄 罗飞 张雍涛 曹涛

(华南理工大学自动化科学与工程学院，广东广州510640)

随着我国经济飞速发展，水资源的短缺和水污染问题的日益加剧，使得提高污水处理厂的污水处理能力和效率成为亟待解决的问题．污水处理厂在保证出水水质达标的前提下，尽可能降低污水处理过程中的能源消耗，是提高污水处理厂污水处理能力和实现节能减排的主要方法．

目前国内外学者在污水生化处理过程的节能优化方面取得了一定的研究成果．日本东芝公司提出了基于分层的最小成本优化控制策略［1］，降低运行成本．瑞典的Amand等［2］通过改变出水氨氮浓度反馈控制器的参数，实现了在入水负荷变化条件下，平均出水氨氮浓度保持在某理想值附近的同时鼓风量最小．西班牙的Cristea等［3］提出一种混合非线性预测控制算法，在满足随时间变化的氧气需求量与出水限制条件下降低能耗．Zhang等［4］采用混合遗传算法设计了一种以实现出水水质限制和使运行成本最低为目标的前馈-串级控制器，对溶解氧浓度和污泥浓度进行控制．史雄伟等［5］采用层级式结构的优化控制系统，用改进的粒子群优化算法确定溶解氧浓度和硝酸氮浓度的设定值，实现对氧传递系数和内循环流量的控制．叶洪涛等［6］设计出了新型的免疫选择算子，应用于简化的污水生化处理状态方程模型上，实现了污水处理过程运行费用的最优控制．

在污水生化处理过程节能优化控制中，如何确定控制变量的最优设定值，是实现系统优化的关键问题．为了避免一般优化算法在寻找最优设定值的过程中遇到“早熟”问题，引入人工免疫算法．它是一种全局寻优算法，利用免疫系统的多样性产生和维持机制来保持群体的多样性，能有效克服“早熟”，同时能增强系统鲁棒性［7］．文中提出一种基于人工免疫算法的污水生化处理过程节能优化策略，通过在不同天气(晴天、雨天和暴雨天)进水数据情况下的仿真实验，验证了该算法的有效性和鲁棒性．

1 污水生化处理系统的节能优化控制

1．1 污水生化处理系统动态数学模型的选择

建立合适的污水生化处理系统动态数学模型是节能优化控制策略实施的前提和基础．首先必须选择能够客观、准确描述污水处理的生物化学反应机理和工艺特点的动态数学模型，然后在此基础上进行节能优化控制策略的设计和仿真实验，这样便可以对所研究的优化策略进行客观、公正的评价．

在研究污水处理系统节能优化的初期阶段，学者们大多采用简化的单变量或两变量活性污泥处理过程基本状态方程作为数学模型［8-9］，由于污水生化处理的非线性、时变、时滞和不确定性，简化的基本状态方程很难全面和准确描述污水反应过程．随着污水生化处理系统动态建模研究的不断发展，能够完整和准确描述污水处理过程的复杂动态数学模型逐步成熟和被认可，该类复杂动态数学模型已经成为当前优化控制算法验证的有效客观平台．

文中采用国际水协会(IWA)提供的基准仿真模型BSM1作为动态数学模型．IWA与欧盟科学技术合作组织(COST)合作开发建立的对污水厂控制策略进行模拟评价的平台BSM1，在国内外学者的研究中被广泛使用，它定义了污水处理的设备布局、仿真模型、污水负荷、测试程序和评价标准．图1为BSM1设备的总体布局，它以IWA活性污泥1号模型为基础［10］，是典型的前置反硝化活性污泥污水处理工艺(A/O工艺)．BSM1模型由2个缺氧池、3个好氧池和1个二沉池构成．它利用悬浮在污水中的微生物群体即活性污泥的吸附和新陈代谢作用来净化污水．在曝气池内活性污泥吸附有机物作为营养源，经氧化和同化作用被微生物利用，其中硝化细菌能在好氧条件下通过硝化反应将氨氮转化为亚硝酸氮和硝酸氮，接着通过混合液回流，硝酸氮在缺氧池中反硝化细菌的作用下被转化为氮气和水．污水经过5个生物反应池后在二沉池中进行污泥沉淀，最上层可作为处理后的出水排入江河，最底层的污泥一部分作为剩余污泥进一步处理，另一部分回流到第一个反应池被重复利用．

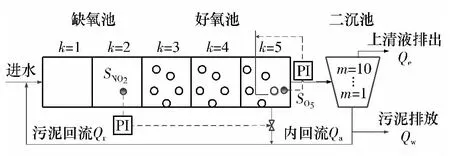
图1 BSM1设备布局Fig．1 Overview of the BSM1 plant

1．2 基于人工免疫算法的节能优化控制策略

1．2．1 污水生化处理系统节能优化策略

在污水生化处理系统中，鼓风机能耗、内回流泵送能耗和污泥外回流泵送能耗是最主要的能源消耗类型．由于污泥外回流量的改变很容易造成二沉池的水力扰动，造成出水水质恶化，污水厂常常维持污泥外回流量恒定或者与进水量成比例控制［11］．因此，文中把节能优化的目标确定为最小化鼓风机能耗和内回流泵送能耗．

污泥生化反应中，好氧池的溶解氧(DO)浓度和缺氧池的硝酸氮浓度是影响硝化和反硝化进程的重要参数，溶解氧浓度的调节是通过调节好氧池末端的氧传递系数来控制DO浓度稳定，氧传递系数和鼓风能耗相关;硝酸氮浓度是通过调节内回流流量Qa来控制缺氧池末端的硝酸氮浓度稳定，内回流量和泵送能耗相关．而鼓风机和泵送的能耗分别占污水处理厂设备能耗的50%～70%和10%～25%［12］，因此，如何合理控制溶解氧浓度和硝酸氮浓度是实现节能降耗的关键．

目前，当前很多污水处理厂的溶解氧和氨氮浓度设定值都是恒定值，它们在相当长时间内(例如一个月或一个季度)保持恒定，包括我们的仿真平台Benchmark模型自带的PI控制器的设定值也是恒定的(它们的设定值分别为2和1 g/m3)．而经过分析可知，针对不同天气状况，不同时间的污水入水数据有很大差异，若溶解氧浓度PI控制器和硝酸氮浓度PI控制器的设定值始终保持不变，则处理后的出水水质和能耗都无法实现最优化．因此，必须对溶解氧浓度SO5(下标5表示5号池)和硝酸氮浓度SNO2(下标2表示2号池)的PI控制器设定值进行最优化设计．根据BSM1模型的建议，首先建立好氧池末端溶解氧浓度SO5的PI控制器和缺氧池末端硝酸氮浓度SNO2的PI控制器，再综合考虑出水水质和运行能耗，结合人工免疫算法对前置反硝化污泥生化处理系统进行优化控制，寻优求解SO5和SNO2的动态设定值，让两个PI控制器跟随优化设定值对氧传递系数和内回流量进行控制，在保证出水水质达标的前提下，最小化能耗成本．

首先定义污水生化处理系统的节能优化目标函数．设一段时间［t，t+T］内的运行能耗E为

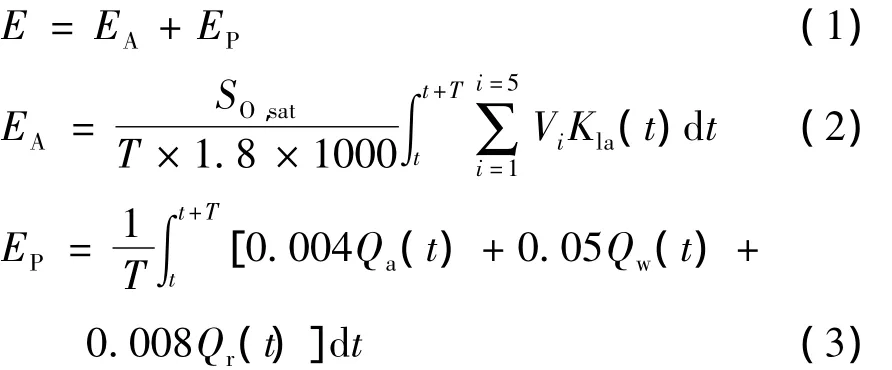
式中，EA为鼓风能耗，EP为泵送能耗，Kla为氧传递系数，Vi为各反应池体积，SO，sat为饱和溶解氧浓度，Qw为污泥排放量，Qr为污泥回流量．

根据IWA的定义，污水生化处理后的出水水质必须满足以下条件:总氮浓度TN＜18 g/m3、化学需氧量COD＜100 g/m3、氨氮浓度 SNH＜4 g/m3、固体悬浮物浓度TSS＜30g/m3、5天生化需氧量BOD5＜10g/m3．

针对污水出水水质必须达标这个约束条件，采用惩罚因子法［13］对出水浓度越限的情况做惩罚处理，使平均浓度越限部分乘以一个较大的惩罚因子．这样一来，越限较大的控制其相应的优化目标函数J值也较大，在寻优过程中就会被淘汰掉．因此优化问题的总目标函数为

式中，ci(i=1，2，…，5)为惩罚因子．

1．2．2 最优设定值的人工免疫优化算法

免疫算法(IA)采用的是群体搜索策略，强调群体中对个体评价的全面性［7］．它对个体的评价是通过计算亲和度得到的，也以此为基础进行个体的选择．个体的亲和度包括抗体-抗原之间的亲和度(匹配度)和抗体-抗体之间的亲和度(相似度)，它们反应了真实的免疫系统的多样性．同时，借助克隆选择、免疫记忆等机理，对抗体的产生进行促进或抑制，即高亲和力抗体受到促进，高浓度抗体受到抑制，体现了免疫反应的自我调节功能，保证了个体的多样性．

定义溶解氧浓度设定值SO5，ref和硝酸氮浓度设定值SNO2，ref为待优化问题的最优解抗体，系统计算输出的目标函数值J为抗体的亲和度．优化过程如下:

(1)令起始时间t=0，优化周期为T．

(2)产生抗体群．在两个设定值取值范围(0 ＜ SO5，ref＜3，0 ＜ SNO2，ref＜4)内随机产生初始抗体种群，将该抗体群中的每个抗体依次赋值给BSM1模型的两个寻优参数 SO5，ref和 SNO2，ref．

(3)运行BSM1系统的 Simulink模型［t，t+T］天，计算得到相应各抗体的性能指标J值，并通过比较输出最优抗体对应的J值(即种群中最小的J值)到IA中作为该抗体的亲和度，同时记录该抗体为最优抗体．

(4)根据免疫操作机理对抗体种群进行更新操作，包括抗体产生的促进和抑制、记忆细胞库的产生以及抗体的选择、克隆和变异．首先将J值最低的若干抗体存入记忆库，同时按期望选择概率从大到小排列抗体，再根据所选的克隆因子决定每个候选克隆抗体的克隆数(与抗体的期望选择概率成正比)，最后依据变异因子对抗体种群进行变异操作．

(5)判断是否达到最大进化代数，若没有则重复步骤(2)-(4);若达到迭代次数或精度要求则退出该次设定值的寻优．输出第t天内最优的SO5，ref和SNO2，ref设定值及J值．至此，第t天的优化进行完毕．

(6)令时间t=t+T，返回步骤(2)进行下一天参数设定值的寻优，直到完成全部所需优化总天数的寻优操作．具体IA优化两个设定值的过程示意图如图2所示．

在步骤(4)抗体的促进和抑制过程中，每个抗体的期望选择概率由抗体与抗原间的亲和度和抗体浓度两部分共同决定，即个体亲和度越高，则期望选择概率越大;个体浓度越大，则期望选择概率越小．这样，在保留高亲和度个体的同时，进一步确保了抗体的多样性，能避免早熟现象［14］．需要说明的是，个体浓度表示某个个体与其他所有个体的相似度，可以通过阈值来实现．文中用con表示个体浓度，J表示抗体亲和度，Pexc为期望选择概率，M为种群规模，第i个抗体的期望选择概率计算公式为

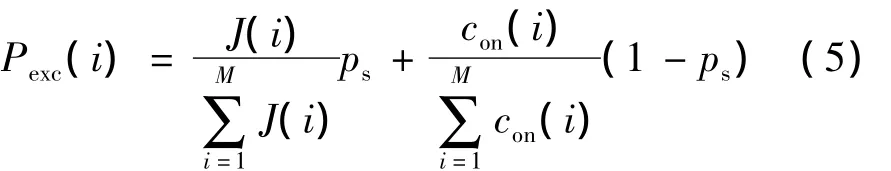
式中，ps为多样性评价参数．

同时考虑到，在抑制高浓度个体时，与抗原亲和度最高的抗体也可能因其浓度高而受到抑制，从而导致已求得的最优解丢失，因此采取精英保留策略，在每次更新记忆库时，先将与抗原亲和度最高的若干抗体存入记忆库中，再按照期望选择概率将其他优秀个体存入记忆库．

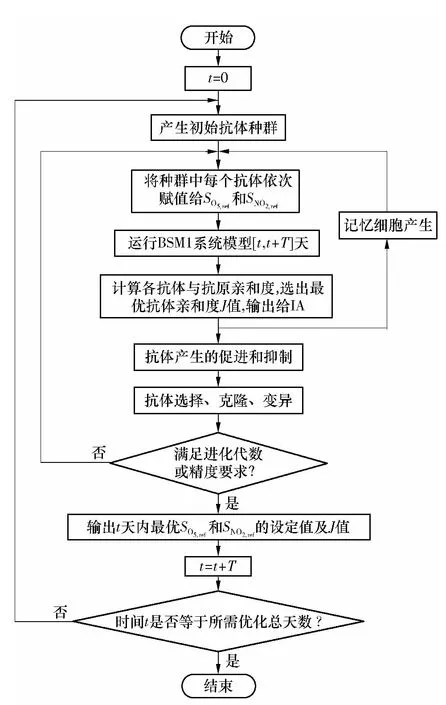
图2 污水处理人工免疫算法流程图Fig．2 Flow diagram of wastewater treatment by using artificial immune algorithm

2 仿真实验和结果分析

为了验证文中提出的污水生化处理系统节能优化控制策略运行效果，在污水生化处理基准仿真模型BSM1上进行了大量仿真实验．BSM1模型的仿真条件如下:缺氧池体积V1=V2=1000m3，好氧池体积V3=V4=V5=1333m3，饱和溶解氧浓度 SO，sat=8g/m3，好氧池氧传递系数Kla3=Kla4=240，污泥回流量Qr=18446m3/d，污泥排放量Qw=385m3/d．

采用IWA与COST提供的城市生活污水数据集进行实验，包括晴天、雨天和暴雨天3种情况，这些污水数据都是由真实操作得到．每组数据由2周的采样数据组成(0～7d表示第一周的周一到周日，7～14 d表示第二周的周一到周日)，采样间隔为15min．图3给出了BSM1模型给定的晴天入水流量曲线，可以看出，周一至周五的数据规律相似，周六和周日入水流量有下降趋势．雨天和暴雨天的情况则在入水流量和持续时间上都有所改变．图4给出了入水水质SNH、TN、BOD5、COD和TSS 5个指标的变化曲线，以便与优化控制后的出水水质作对比．

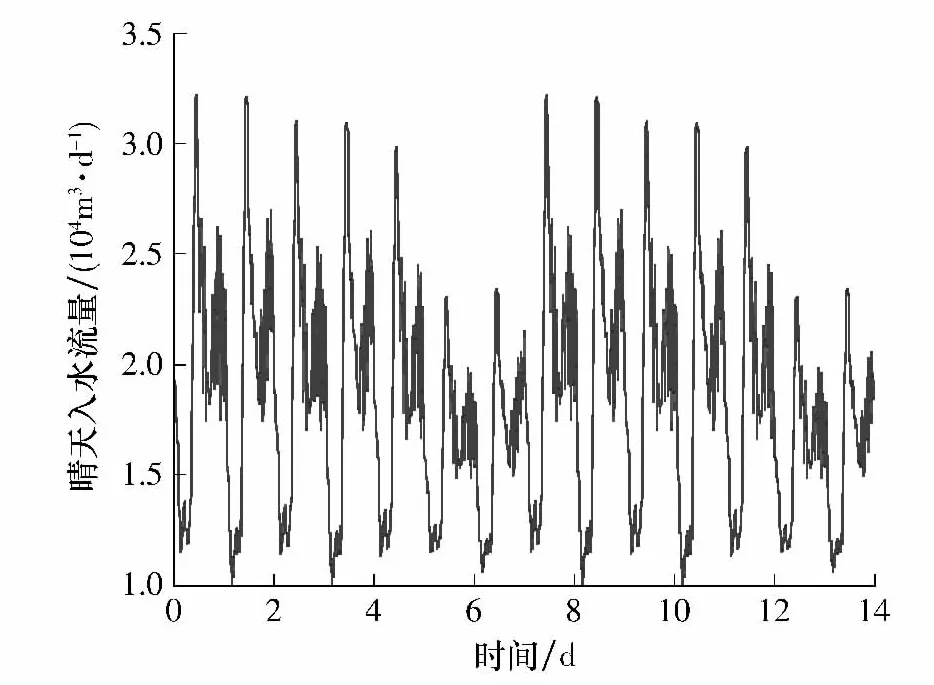
图3 晴天入水流量变化曲线Fig．3 Influent flow rate curve of dry weather

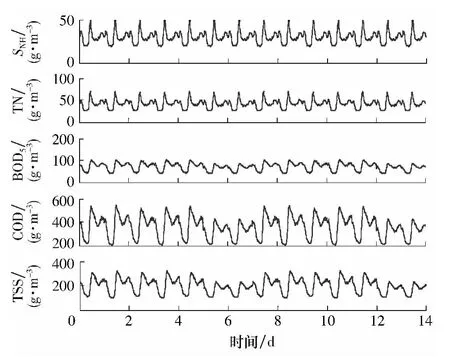
图4 晴天入水污染物浓度变化曲线Fig．4 Influent pollutant concentration curves of dry weather

考虑到污水生化处理系统存在较大的滞后性，不是越高强度的优化频率就能达到越好的控制效果．根据BSM1的模型设计，晴好天气条件下日平均进水流量为18446m3/d，生化反应池和二沉池的总体积为 12000m3，则模型的水力停留时间约为 14．4h［15］．因此，在寻优过程中文中将在优化周期的基础上加入0．6d的滞后时间作为某次寻优的运行时间，以期得到更接近客观实际的最优设定值．同时，根据入水数据以天为单位具有一定的周期性，文中选定优化周期T=1d，即针对任意为期两周的入水动态数据，将分别寻找出针对每一天的溶解氧浓度SO5和硝酸氮浓度SNO2优化设定值，从而得到各参数14d内的动态调整曲线．

本次实验免疫优化算法的基本参数选定为:种群规模M=20、记忆库容量m=6、迭代次数Gen=20、克隆因子 Pc=0．1、变异因子 Pm=0．5、多样性评价参数ps=1．2，同时通过反复实验可知，TN和SNH的越限几率较大，文中根据经验选取惩罚因子c1=c2=500，c3=c4=c5=100．

文中分别在晴天、雨天和暴雨天3种情况下，以式(4)为总优化目标函数，进行了好氧池溶解氧浓度SO5的PI控制器和缺氧池硝酸氮浓度SNO2的PI控制器最优设定值的寻优计算，求出最优设定值后，把计算出的最优值赋值给两个PI调节器的给定端，调节氧传递系数和内回流量，简称优化控制Ⅰ．当整个污水处理过程运行完成后，计算污水系统整体能耗数值并分析结果．为了方便对比分析，文中采用好氧池溶解氧浓度SO5的PI控制器设定值恒为2g/m3、缺氧池硝酸氮浓度SNO2的PI控制器设定值恒为1g/m3的常规控制策略［16］进行同样的仿真实验，简称常规控制．

优化控制Ⅰ算法在晴天情况下按人工免疫优化方法可以得到2周内每天的SO5和SNO2最优设定值，其整体走势如图5所示．由图5中可知，每天的最优SO5和SNO2设定值都不相同，设定值在周一至周五处于高位波动，周六和周日随着入水流量的减少有下降趋势，周二处于最高位．这是由于周末设定值减小和周一的入水流量增加，造成在周二的污水处理量达到最高值，把相应的控制器设定值调高，才能保证污水处理正常运行并使出水水质达标．图6为5个出水水质指标两周内的波动情况，与图4比较可看出系统的去污效果显著．

图5 晴天时优化控制Ⅰ的SO5和SNO2的最优动态设定值Fig．5 Best setting values of SO5and SNO2in dry weather condition after the optimal controlⅠ

图6 晴天时优化控制Ⅰ的出水水质Fig．6 Effluent concentration curves of dry weather condition after the optimal controlⅠ

表1给出了3种天气情况下出水水质指标排放浓度的平均值．表2列出了能耗对比情况．

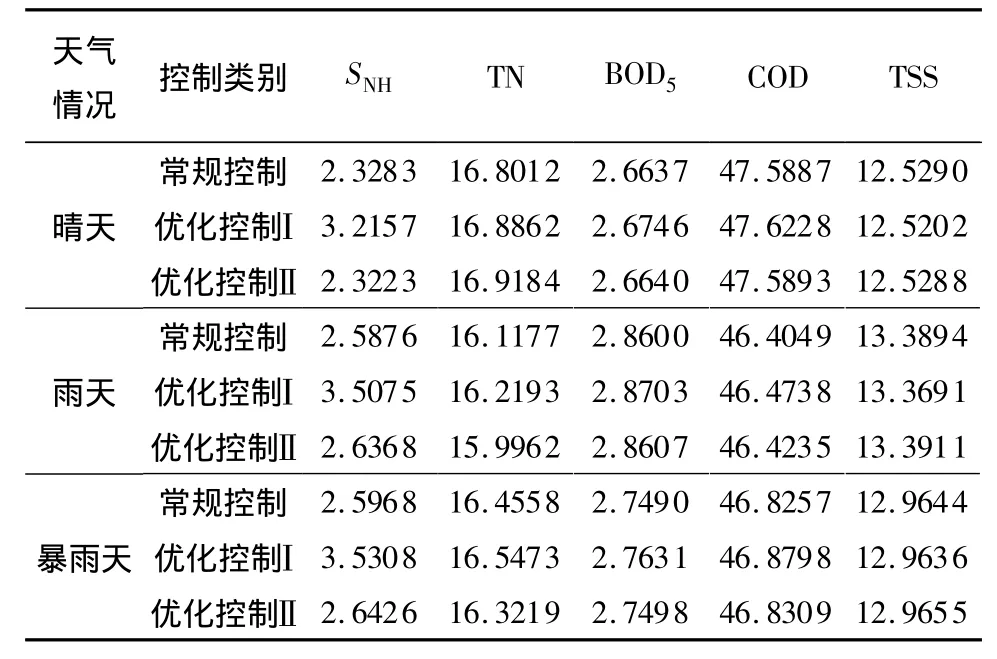
表1 3种天气条件下的出水水质平均浓度Table 1 Average effluent concentration under three weather conditions g/m3

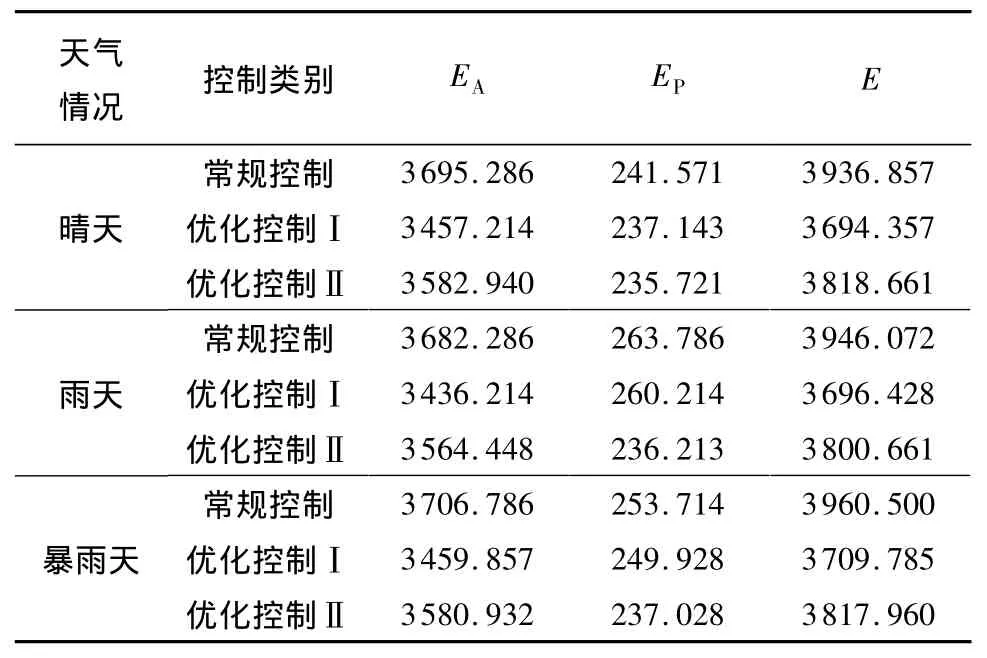
表2 3种天气条件下的能耗比较Table 2 Energy consumption comparison underthree weather conditions kWh/d

晴天条件下，优化控制Ⅰ和常规控制的出水水质均能达到排放标准，其中出水硝酸氮浓度在优化控制Ⅰ下有所升高，但也满足SNH＜4 g/m3的出水水质标准．鼓风能耗比常规控制下减少了6．44%，泵送能耗减小了1．7%，每日总运行能耗减少了6．16%．同样地，在雨天和暴雨天气条件下，出水水质均能达到排放标准，出水硝酸氮浓度在优化控制Ⅰ下接近但不超越硝酸氮的出水水质标准临界值．雨天鼓风能耗比常规控制下减少了6．68%，泵送能耗减小了1．36%，每日总运行能耗减少了6．34%;暴雨天的鼓风能耗比常规控制下减少了6．66%，泵送能耗减小了 1．5%，每日总运行能耗减少了6．33%．这表明文中提出的人工免疫优化控制策略在保证出水水质不越界的前提下，在3种天气情况下都能实现节能．

分析优化控制Ⅰ和常规控制的仿真结果可知，以晴天为例，在常规PI控制下，处理后的出水水质参数硝酸氮SNH平均值约为2．3 g/m3，而优化控制Ⅰ下约为3．2 g/m3，即出水水质浓度有所上升．该值虽然满足IWA的出水水质要求(SNH＜4 g/m3)，但对于判断文中优化算法的节能效果会产生一定的干扰．为了更加客观地验证文中优化算法的节能效果，对优化总目标函数进行修改，将式(4)改写成:

其他仿真条件不变．该算法简称优化控制Ⅱ．目的是使常规控制和优化控制Ⅱ的出水水质都保持在相同的指标上，再进行能耗对比．仿真实验仍采用两周的晴天、雨天和暴雨天气3种数据进行测试，结果见表1和表2．

对比优化控制Ⅱ和常规控制结果发现，两种控制策略下的出水水质均能达到排放标准．在晴天条件下，优化控制Ⅱ的出水水质在达到与常规控制下相近时，鼓风能耗比常规控制下减少了3．04%，泵送能耗减少了 2．42%，每日总运行能耗减少了3．00%;雨天的鼓风能耗比常规控制下减少了3．20%，泵送能耗减少了10．45%，每日总运行能耗减少了3．68%;暴雨天的鼓风能耗比常规控制下减少了3．40%，泵送能耗减小了6．58%，每日总运行能耗减少了3．60%．由此证明了文中提出的优化控制策略在保证相同出水水质指标前提下在节能方面的有效性．

优化控制Ⅱ是为了客观对比两种控制策略的节能效果而进行的实验，而在实际污水处理系统中，往往是希望控制出水参数接近但不超过满足IWA要求的限制值的同时，尽可能地降低能耗，因此，优化控制Ⅰ的实用价值和意义更大．

3 结语

以IWA提供的基准仿真模型BSM1为基础，综合考虑出水排放标准和运行能耗，建立污水生化处理系统的节能优化目标函数，将人工免疫算法引入污水生化处理过程的优化控制中，对好氧池末端溶解氧浓度的设定值和缺氧池末端硝酸氮浓度的设定值进行动态调整．该免疫算法利用了免疫系统的多样性产生和维持机制、克隆及记忆机理来保持群体的多样性，实现全局最优．与常规控制策略相比，在3种入水数据条件下，污水排放均符合标准，且污水处理过程能耗都有明显降低，显示了该优化方法的有效性和鲁棒性．

［1］Yamanaka O，Obara T，Yamamoto K．Total cost minimization control scheme for biological wastewater treatment process and its evaluation based on the cost benchmark process［J］．Water Science and Technology，2006，53(4/5):203-214．

［2］Amand L，Carlsson B．Optimal aeration control in a nitrifying activated sludge process［J］．Water Research，2012，46(7):2101-2110．

［3］Cristea S，Prada C，Sarabia D，et al．Aeration control of a wastewater treatment plant using hybrid NMPC［J］．Computers and Chemical Engineering，2011，35(4):638-650．

［4］Zhang P，Yuan M，Wang H．Improvement of nitrogen removal and reduction of operating costs in an activated sludge process with feedforward-cascade control strategy［J］．Biochemical Engineering Journal，2008，41(1):53-58．

［5］史雄伟，乔俊飞，苑明哲．基于改进粒子群优化算法的污水处理过程优化控制［J］．信息与控制，2011，40(5):698-703．Shi Xiong-wei，Qiao Jun-fei，Yuan Ming-zhe．Optimal control for wastewater treatment process based on improved particle swarm optimization algorithm ［J］．Information and Control，2011，40(5):698-703．

［6］叶洪涛，罗飞，许玉格，等．基于新型免疫算法的污水处理过程最优控制［J］．华南理工大学学报:自然科学版，2010，38(2):139-141．Ye Hong-tao，Luo Fei，Xu Yu-ge，et al．Optimal control of wastewater treatment process based on novel immune algorithm［J］．Journal of South China University of Technology:Natural Science Edition，2010，38(2):139-141．

［7］莫宏伟，左兴权．人工免疫系统［M］．北京:科学出版社，2009:580-581;187-192．

［8］冯裕钊，龙腾锐，郭劲松，等．变参数活性污泥系统的最优鲁棒控制法［J］．中国给水排水，2003，19(3):14-16．Feng Yu-zhao，Long Teng-yue，Guo Jin-song，et al．Optimal robustness control method of activated sludge system based on uncertain parameters［J］．China Water and Wastewater，2003，19(3):14-16．

［9］彭永臻，王宝贞，王淑莹．活性污泥法的多变量最优控制［J］．环境科学学报，1998，18(1):12-19．Peng Yong-zhen，Wang Bao-zhen，Wang Shu-ying．Multivariable optimal control of activated sludge process［J］．Environment Science，1998，18(1):12-19．

［10］Henze M，Jr C G，Gujer W，et al．Activated sludge model No．1 ［R］．London:IAWQ Scientific and Technical Report No．1，1986．

［11］Gustaf Olsson．污水系统的仪表、控制和自动化［M］．马勇，彭永臻，译．北京:中国建筑工业出版社，2007:102-107．

［12］曹珊，曹秀芹．城市污水处理厂能耗分析及节能降耗途径研究 ［J］．给水排水，2012，38(S1):90-92．Cao Shan，Cao Xiu-qin．The research on energy consumption analysis and energy saving approach of urban wastewater treatment plant［J］．Water＆ Wastewater Engineering，2012，38(S1):90-92．

［13］蒋金山，何春雄，潘少华．最优化计算方法［M］．广州:华南理工大学出版社，2007．

［14］Dasgupta D．Artificial immune systems and their applications［M］．BerIin HeideIberg:Springer-VerIag，1999．

［15］Jeppsson U，Rosen C，Alex J，et al．Towards a benchmark simulation model for plant-wide control strategy performance evaluation of WWTPs［J］．Water Science and Technology，2005，53(1):287-295．

［16］王晓莲，彭永臻，马勇，等．污水厂控制策略的国际评价基准［J］．中国给水排水，2004，20(11):32-35．Wang Xiao-lian，Peng Yong-zhen，Ma Yong，et al．International evaluation benchmark on control strategies of wastewater treatmentplan ［J］．ChinaWaterand Wastewater，2004，20(11):32-35．