小角前向散射激光测粒仪探测器偏心对颗粒粒径测量的影响

王玉

小角前向散射激光测粒仪探测器偏心对颗粒粒径测量的影响

王玉

(上海第二工业大学理学院,上海201209)

基于Mie散射理论的小角前向散射激光测粒技术已广泛应用于各种领域。在该测粒技术中要求光电探测单元中心与入射光轴严格对中,以保证测得的散射光能分布及所得粒径分布的准确性,然而在实际测量中很难保证精确对中。利用Mie散射理论,通过模拟计算研究对中不良(主要是偏心)对测量结果的影响,并对结果进行了分析。

前向散射;颗粒测量;Mie散射理论;偏心;模拟计算

0 引言

随着科技的日益进步和发展,在诸如能源、动力、机械、医药、化工、轻工、冶金、建材等行业中出现了越来越多的与细微颗粒密切相关的技术问题,颗粒粒径的测量则是其中最基本也是最重要的一个方面。因此,众多颗粒测试技术应运而生,包括筛分、显微镜成像、沉降、电感应、光散射等。其中,前向小角度激光散射测粒技术最为成熟,得到了广泛的应用[1]。该技术利用Mie散射理论(或Fraunhofer衍射理论),在前向小角度范围内接收散射光,经数据处理后得到待测颗粒的粒径大小及分布信息。

小角前向散射测粒技术中的对中问题很早就引起了人们的重视并作了模拟计算研究,得出一些对实际测量有价值的结果。其方法为:对于某粒径的颗粒,利用Mie散射理论计算对中不良时光电探测器各环接收的光能分布,将所得光能分布作为模拟量进行优化反演;反演时在初始试探粒径的基础上通过不断迭代寻求一个粒径,使其对应的对中良好时的光能分布与被测粒径对应的对中不良时的光能分布最为接近,则该粒径即为最终测量出的粒径;最后把测量结果与实际粒径进行比较分析[2]。对中良好和对中不良状态下光能分布的计算和比较只考虑了单个粒径(理想的单分散系)的情况。然而,在实际应用中,颗粒系并不是单一粒径的,通常分布在一定的粒径范围内。另外,即使是单一粒径的颗粒,其散射光在偏心情况下的分布也不对应严格对中情况下单一粒径的散射光分布。因此,本文通过颗粒粒径分布的计算机模拟计算,研究光电探测器的偏心问题。

1 小角前向散射测粒技术的基本原理

激光散射测粒技术的装置如图1所示。由激光器发出的光束经针孔滤波及扩束器后成为一平行单色光。当该平行光照射到测量区中的颗粒群时会产生光散射现象。散射光的强度分布与入射光波长、测量区中被照射的颗粒直径和折射率有关。散射光信号经过傅里叶透镜后投射到位于焦平面上的多元光电探测器并转换成相应的电信号。电信号经放大和模数转换后送入计算机。根据测得的各个探测单元上的散射光能,通过反演算法可快速得出被测颗粒的粒径大小及其分布。

光电探测元件一般由数十个半圆环组成,中心开有一个小孔供对中之用,与之同心的半圆环则分别接收不同散射角范围的散射光能,如图2所示。

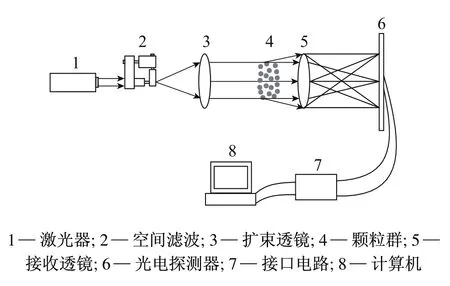
图1 激光测粒技术原理图Fig.1 Schematic diagram oflaser particle analyzer

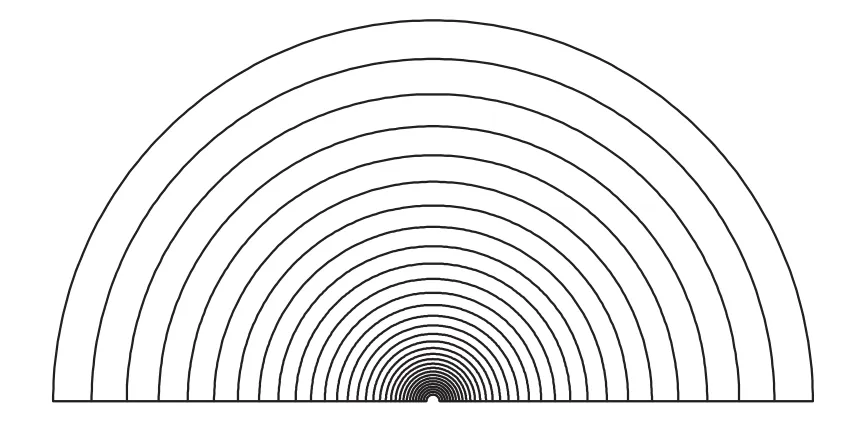
图2 多元光电探测器示意图Fig.2 Sketch map of Mutli-elementphotodetector

为了能准确测量待测颗粒的粒径大小及其分布信息,光电探测元件应与入射光轴严格对中,对中不良会带来测量误差。通常情况下,光电探测器的对中依靠中心设置的小孔,如图2所示的半圆环状探测器。有些颗粒测试仪器在光电探测器的中心设置几个对称的探测单元,例如德国Sympatec公司在光电探测器中心设置了3个探测单元(见图3)。平行入射光经透镜会聚后在焦点上形成一个艾里斑,当严格对中时,这3个探测单元上的光能应相互一致。然而,这两种不同的对中装置都存在各自的缺点。前者由于中心孔径自身的大小难以确保严格对中,其偏心范围与中心孔径的半径有关。对于后者,由于光束自身的质量等问题也会导致一定程度的偏心。而且,在测量时投射到这些探测单元上的光很强,会对光电探测器内侧几环的测量带来影响。

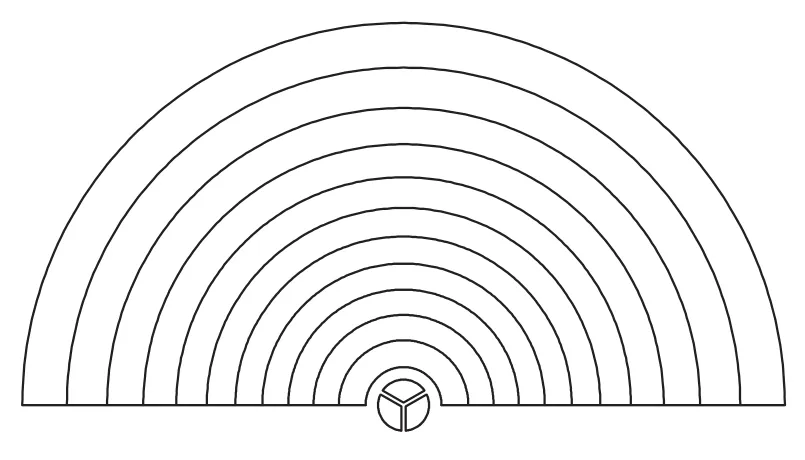
图3 用于对中调整的中心探测器Fig.3 Center photodetector for alignment

根据Mie散射理论[3],当一束强度为I0的自然光入射到各向同性的球形颗粒时,其散射光强为

式中:λ为入射光在粒子周围介质中的波长;R为散射体(颗粒)到观察点的距离;i1、i2分别为垂直及平行于散射平面的散射强度函数;θ为散射角;α=πx/λ为无因次尺寸参数,x为颗粒粒径; m=n-iη为粒子相对于周围介质的复数折射率(虚部不为零时表示粒子有吸收),实部n(称为折射系数)反映了介质的折射(散射)特性,虚部η(称为吸收系数)反映了介质对光波的吸收特性。

由式(1)可求出单个颗粒在多元光电探测器第i环上的散射光能

式中:i12(α,m,θ)=i1(α,m,θ)+i2(α,m,θ);C为常数;θin,i(θout,i)为第i环内半径(外半径)对应的散射角;ρin,i(ρout,i)为第i环的内半径(外半径);f为透镜焦距;φ为方位角。对于具有一定分布的颗粒系,可以得到

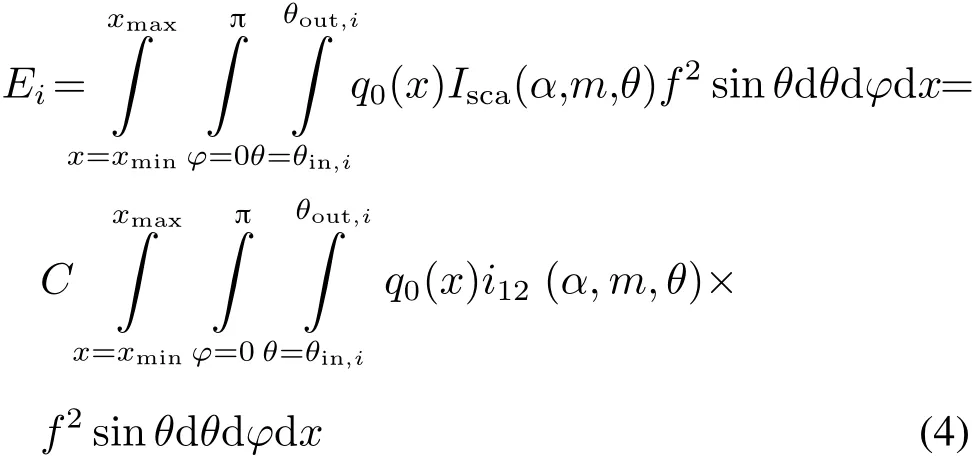
式中,q0(x)为颗粒粒径的分布函数。在小角前向散射测粒技术的反演计算中,一般采用颗粒粒径的二维分布函数q2(x)(即颗粒面积或表面积分布函数)[4]。因此,式(4)又可以表示为

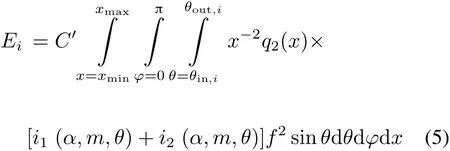
式中,C′为常数。在小角前向散射测粒技术中,颗粒系的粒径分布是从散射光能的分布得到,而不是由散射光能的绝对大小决定。因此,这些常数可忽略不计。式(5)是第一类Fredholm积分方程,在实际应用中通常作离散化处理[5]。

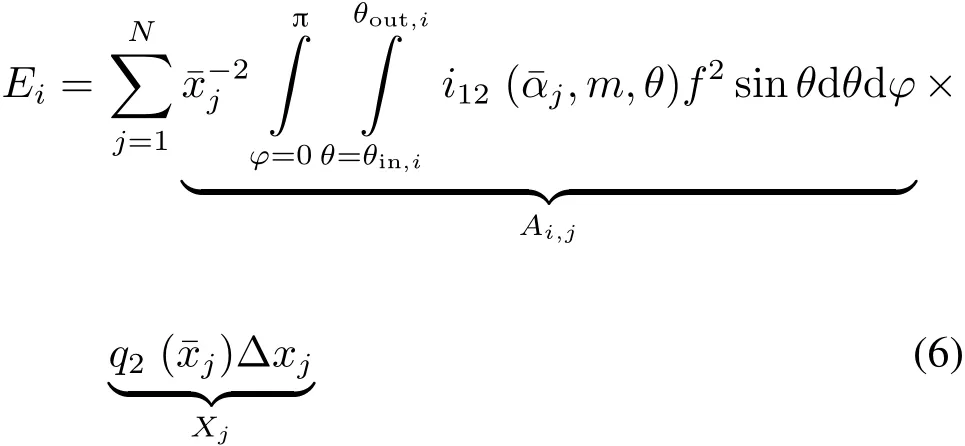
式中:¯xj是第j个粒径区间的平均粒径;¯αj=π¯xj/λ是对应于¯xj的无因次平均尺寸参数;Δxj是第j个粒径区间的宽度;Ai,j是对应于第i个环和第j个粒径区间的矩阵元,由Mie理论计算得到;Xj是粒径分布。式(6)最终可写成

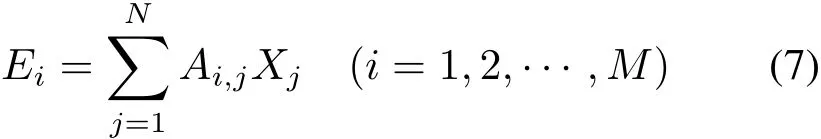
式(7)给出了散射光能分布和颗粒粒径分布之间的一种联系,散射光能分布从实验中测得后,通过反演计算可得颗粒粒径分布。但由于对中不良,导致了散射光能分布偏离对中良好时的光能分布。因此,通过反演计算得到的粒径分布必然也产生偏差。

本文中光电探测元件的中心小孔半径为0.149 mm,半圆环数为31,各环内外径参数见表1。

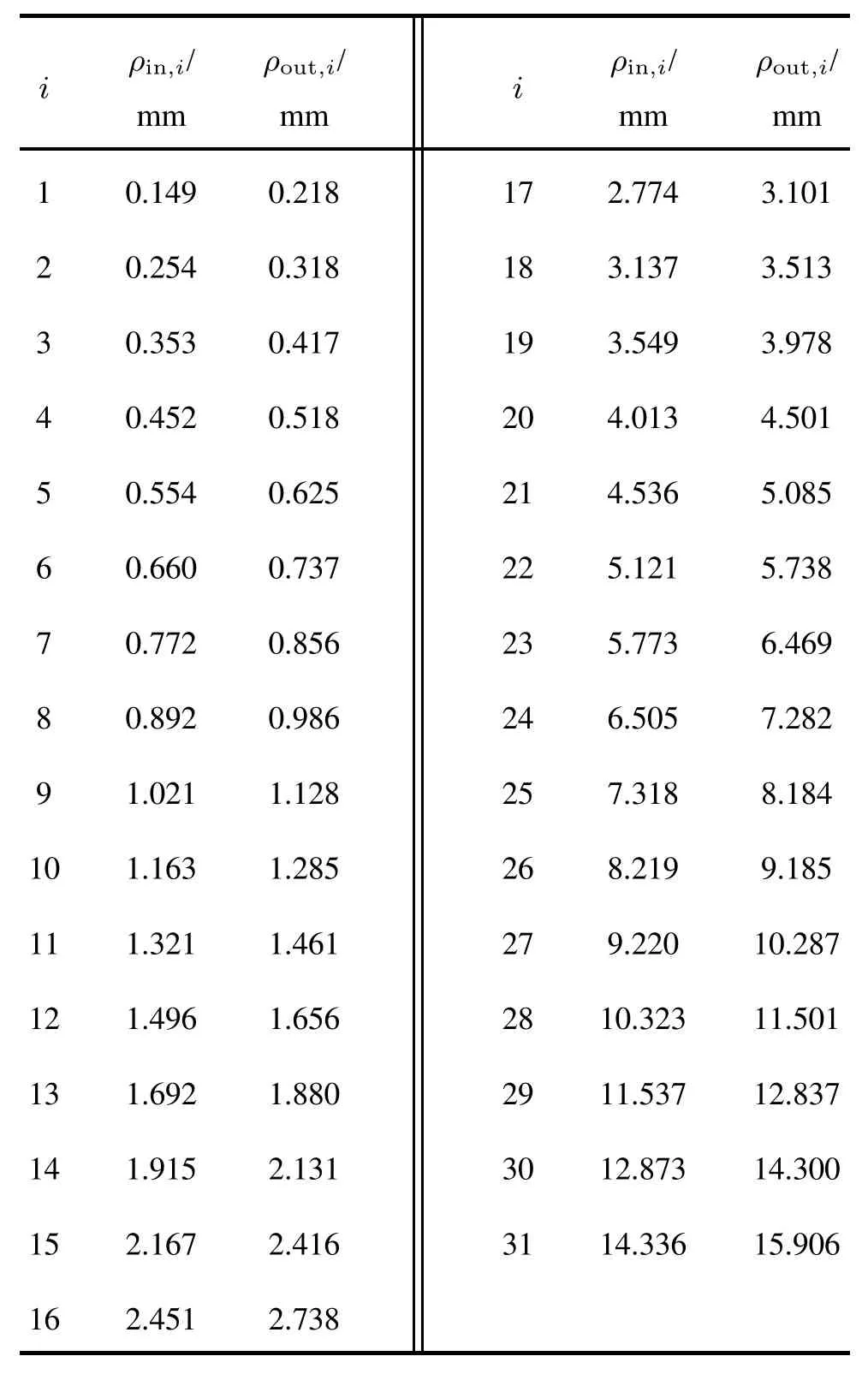
表1 光电探测器尺寸Tab.1 Dimension ofmutli-elementphotodetector

2 对中误差的计算模型

小角前向散射测粒仪的对中不良一般分为偏心和倾斜两种情况,即光电探测器中心偏离光轴和光电探测器与入射光轴不垂直。通常情况下,偏心导致的误差比倾斜导致的误差大[2]。因此,调节光电探测元件的对中以降低偏心程度显得更为重要,本文仅对偏心情况加以讨论。

图4给出了对中良好情况在笛卡尔坐标系中的示意图,O为坐标原点,入射光轴(OV)与Z轴重合。多元光电探测器位于XY平面内,与Y轴对称且沿Y轴正向放置,此时多元光电探测器各环的几何中心与坐标原点O重合。

图5为偏心情况下的示意图,图5(a)为三维图,图5(b)为图5(a)的俯视图。D为光电探测元件受光面上的任意一点,ρ为OD的长度,φ为OD与X轴的夹角,V为入射光轴与光电探测元件接收平面的垂直交点,称为入射光的偏心点(一般情况下V点总是位于小孔内部);ψ为OV与X轴的夹角(称为偏心角),r为偏心点离原点O的距离(称为偏心距)。偏心的存在导致实际测得的颗粒散射光能分布与对中良好时对应的光能分布存在偏差,其光能分布的计算公式可由严格的理论推导得到。

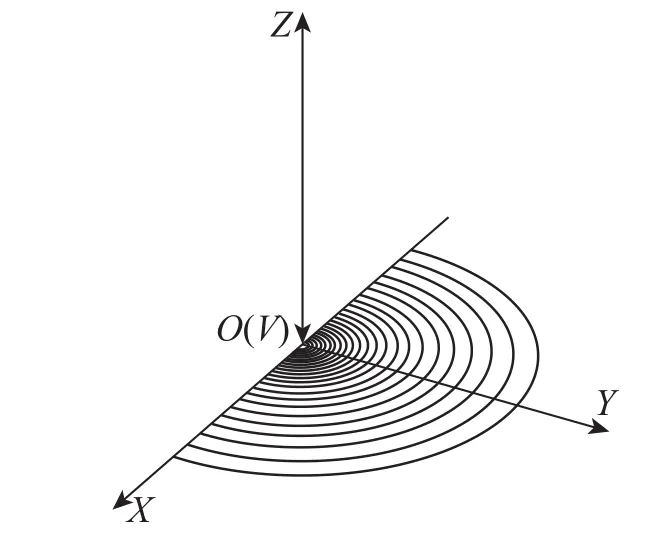
图4 对中良好情况的示意图Fig.4 Sketch map of good alignment

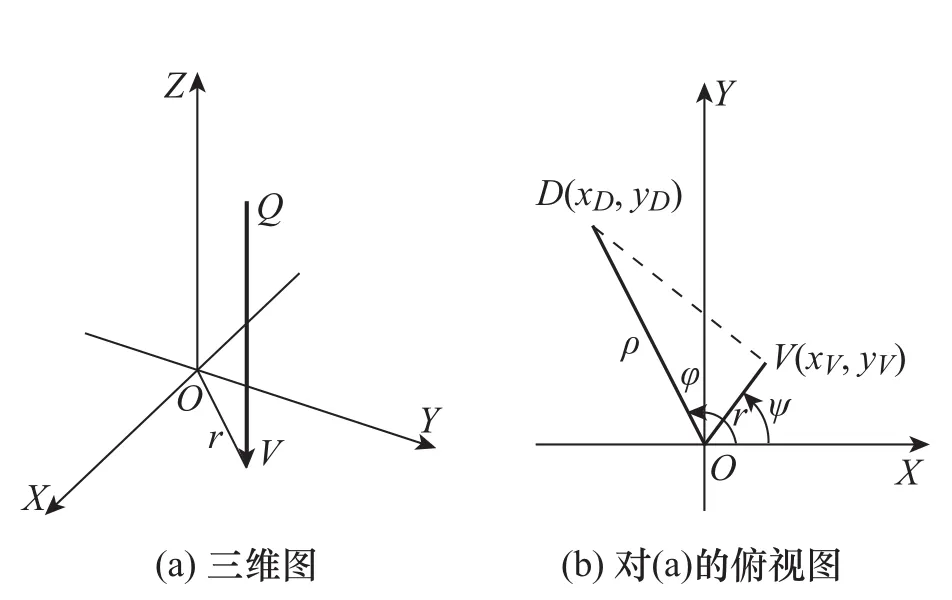
图5 偏心情况的示意图Fig.5 Sketch map of eccentricity

首在给出V点在极坐标系中的表示:

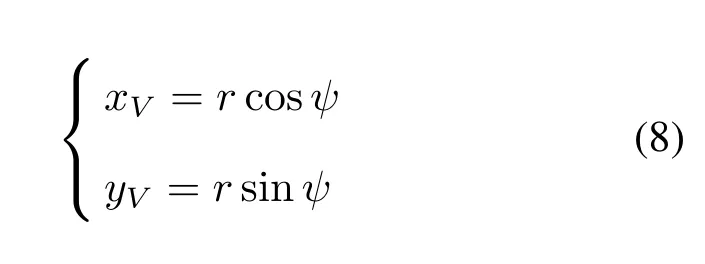
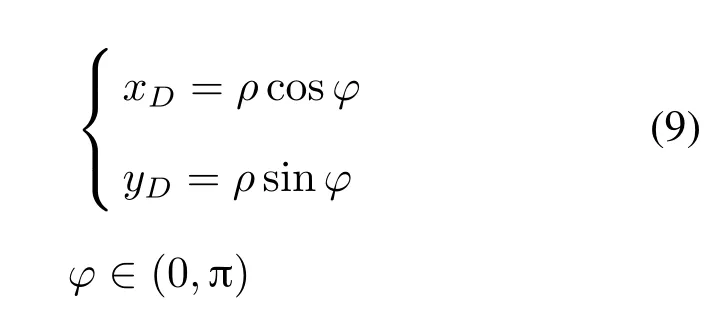
由此可得DV的长度:

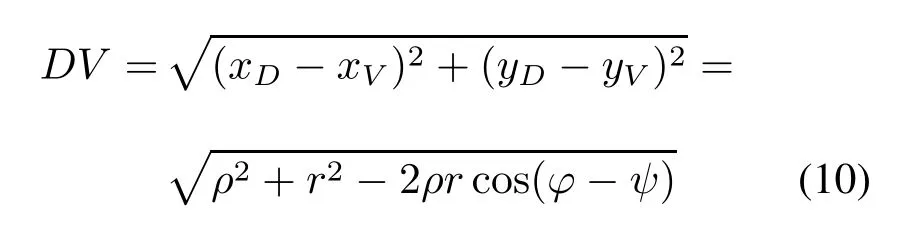
和偏心时散射角

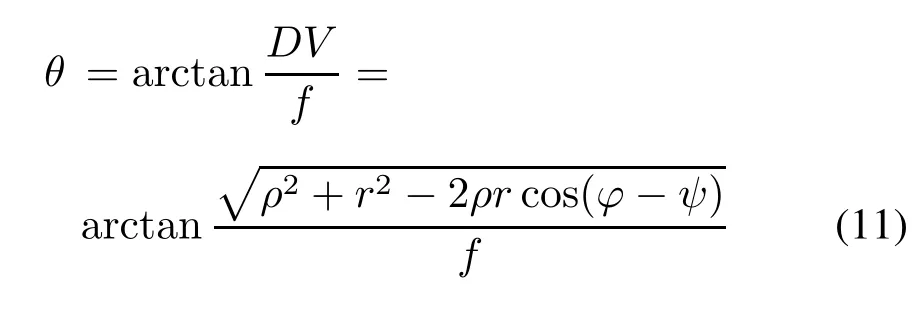
通过式(1)可计算偏心情况下的散射光强。其中,散射颗粒到接收点的距离为

由式(8)～(12)可得单个颗粒在偏心情况下各探测单元的散射光能

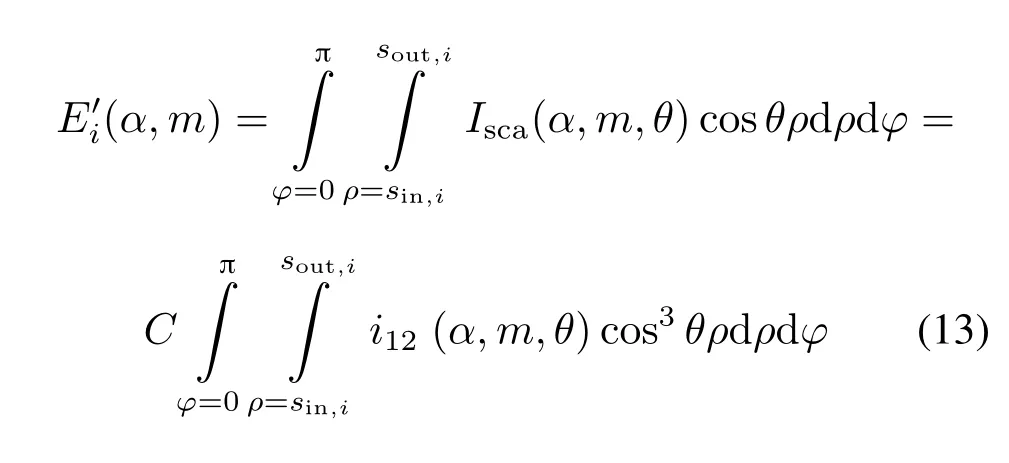
类似式(2)～式(5)的分析,同样可以得到偏心情况下颗粒系在各探测单元的散射光能

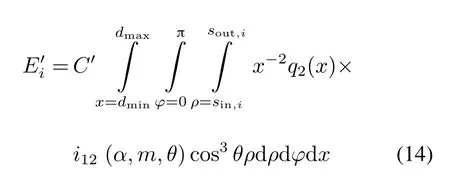
由式(14)可模拟计算出偏心情况下颗粒系散射光能在光电探测元件各环上的实际分布情况。

3 计算机模拟计算过程及结果分析

为简便起见,本文的模拟计算只考虑颗粒的二维分布服从高斯分布的情况。具体模拟过程如下:

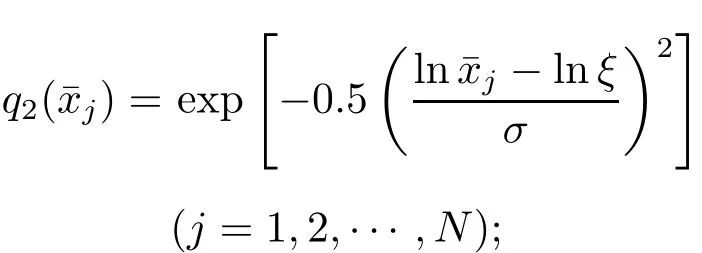
(2)计算Sauter平均粒径

(3)设定具体参数f,m;

(4)选取一种偏心情况,即选定偏心距r和偏心角ψ;

(5)利用式(14)计算出偏心情况下颗粒散射光能在光电探测器各环上的分布E′i,并作为模拟量用于反演计算;

(6)将E′i取代式(7)中的Ei,得到

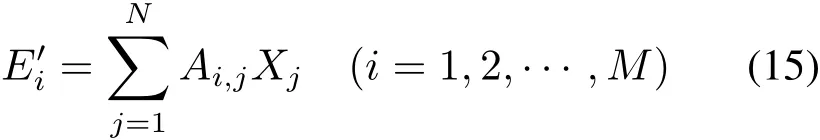
(7)采用独立模式反演方法计算式(15),最终反演出粒径分布Xj及其Sauter平均粒径,本文中采用了chahine反演方法[6]。

计算机模拟结果如下。

图6是焦距为63 mm、折射率为1.33、偏心角为-90°时,不同平均粒径ξ的情况下,光电探测器偏心对单分散系的粒径分布及Sauter平均粒径的影响。可以得出:

(1)对于同一颗粒系,所得粒径分布随着偏心距r的增大逐渐地偏离无偏心时所得的粒径分布。

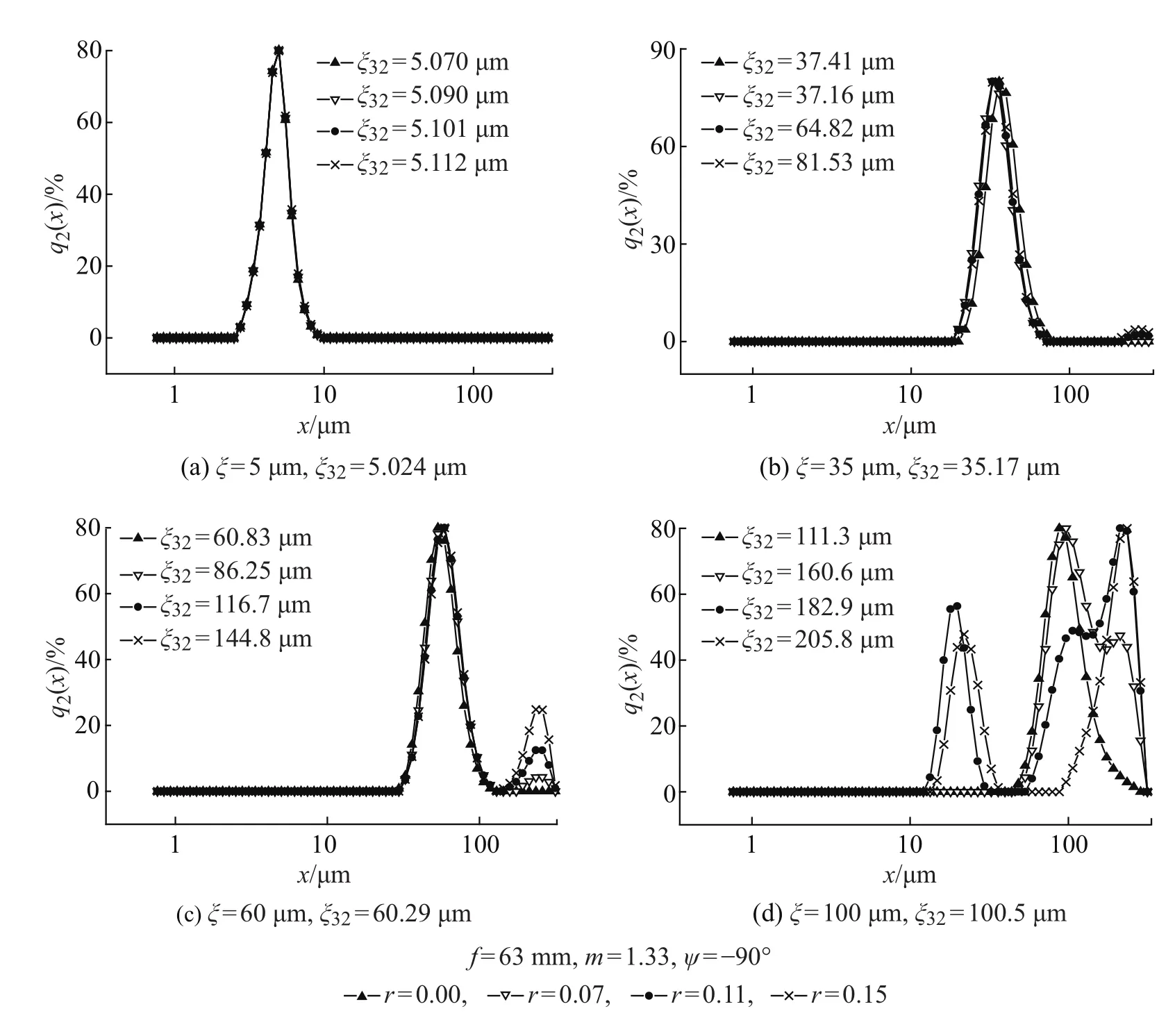
图6 负偏心角时偏心对不同平均粒径的单分散颗粒系的影响Fig.6 Influence of negative eccentricity on results of measurementfor differentmonodisperse particle systems

(2)对于不同的颗粒系,图6(a)是平均粒径为5µm、ξ32=5.024µm的情况下,偏心时所得粒径分布与无偏心时所得粒径分布重合得很好;图6(b)是平均粒径为35µm、ξ32=35.17µm的情况下,偏心时反演出的粒径分布在大粒径范围新出现了一个小的分布,在整个粒径范围呈现微弱的双峰分布,与无偏心时反演出的粒径分布有较小的偏离;图6(c)是平均粒径为60µm、ξ32=60.29µm的情况下,偏心时反演出的粒径分布在大粒径范围出现了一个较大的分布,在整个粒径范围呈现出明显的双峰分布,与无偏心时反演出的粒径分布有较大偏离;图6(d)是平均粒径为100µm、ξ32=100.5µm的情况下,偏心时反演出的粒径分布明显与无偏心时反演出的粒径分布有更悬殊的偏离。这说明,在同样的偏心情况下,所得颗粒粒径分布与无偏心时粒径分布的偏离程度以及颗粒的平均粒径有关,颗粒越大,偏离程度越大。

(3)与颗粒粒径分布相对应,Sauter平均粒径也呈现出相应的偏离规律。偏心时所得的Sauter平均粒径要比无偏心时的Sauter平均粒径偏大。对于同一颗粒系,Sauter平均粒径随着偏心距r的增大逐渐地偏离无偏心时的值。在同一偏心距的情况下,不同颗粒系的Sauter平均粒径的偏离程度随平均粒径的增大而增大。

因此可以得出:测量的颗粒越大,偏心导致的影响越大;偏心距越大,偏心导致的影响越大;负偏心角时,反演出的粒径分布的Sauter平均粒径偏大。

图7是焦距为63 mm、折射率为1.33、偏心角为90°时,不同平均粒径情况下,光电探测器偏心对单分散系的粒径分布及Sauter平均粒径的影响。可以看出:

(1)从粒径分布的角度,图7(a)是平均粒径为5µm、ξ32=5.024µm的情况下,偏心时反演出的粒径分布与无偏心时反演出的粒径分布重合得很好;图7(b)是平均粒径为35µm、ξ32=35.17µm的情况下,偏心时反演出的粒径分布在基本保持单分散系分布的基础上向小粒径方向有微小偏移,与无偏心时反演出的粒径分布偏离较小;图7(c)是平均粒径为60µm、ξ32=60.29µm的情况下,偏心时反演出的粒径分布与35µm情况相比,向小颗粒方向偏移得较多;图7(d)是平均粒径为100µm、ξ32= 100.5µm的情况下,偏心时反演出的粒径分布与60µm情况相比,向小颗粒方向偏移更多;另外,类似负偏心角情况,在正偏心角时,随着偏心距的增大,偏心时反演出的粒径分布也在逐渐地偏移无偏心时反演出的粒径分布,并且这种偏离的程度随着平均粒径的增大而增大。

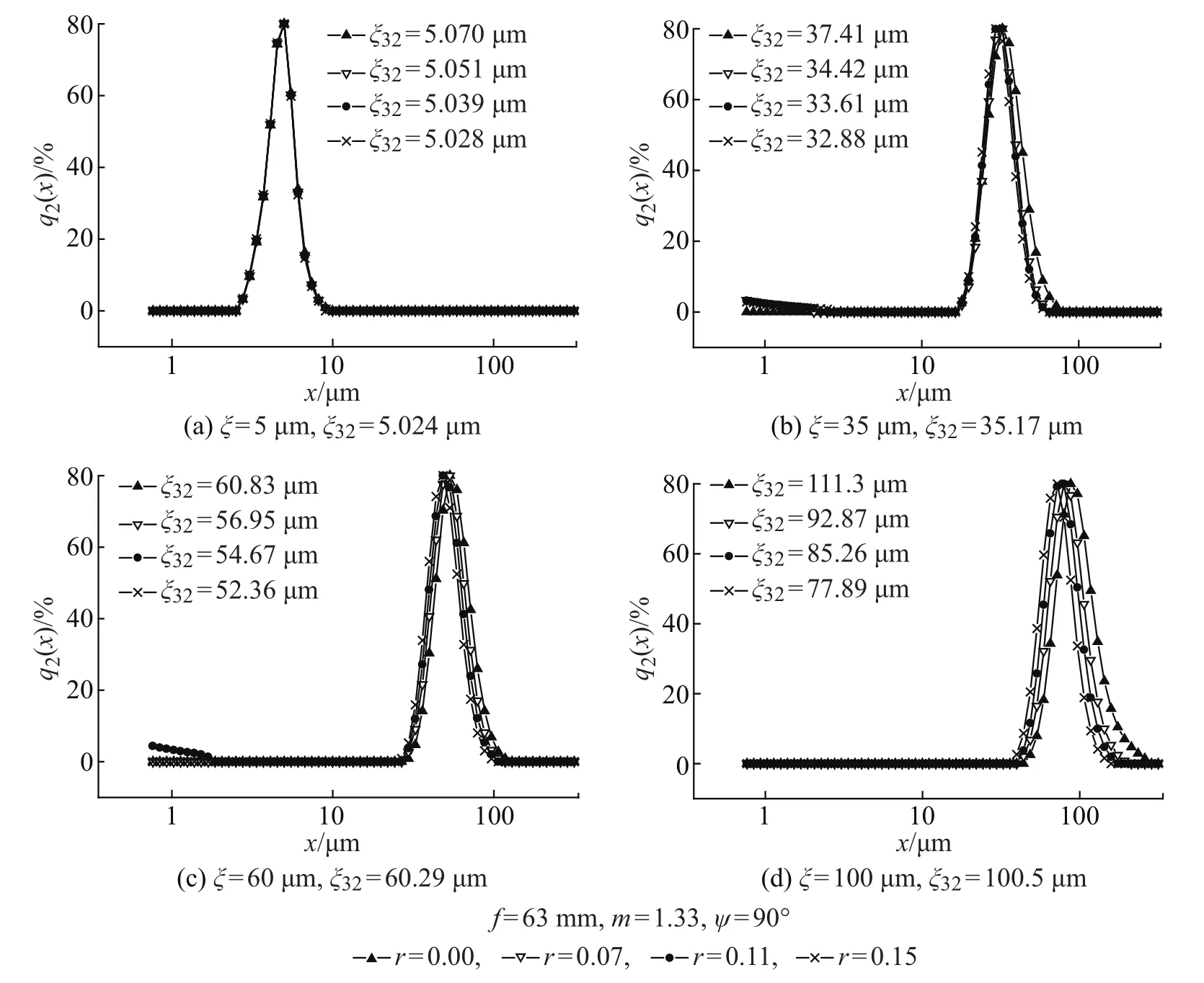
图7 正偏心角时偏心对不同平均粒径的单分散颗粒系的影响Fig.7 Influence of positive eccentricity on results of measurementfor differentmonodisperse particle systems

(2)从Sauter平均粒径的角度,偏心时反演出的粒径分布的Sauter平均粒径要比无偏心时反演出的粒径分布的Sauter平均粒径偏小。同一平均粒径,随着偏心距r的增大,反演出的粒径分布的Sauter平均粒径越加地偏离无偏心时的情况。另外,由于偏心距导致的Sauter平均粒径的偏离程度随着平均粒径的增大而增大。

因此可以得出:测量的颗粒越大,偏心导致的影响越大;偏心距越大,偏心导致的影响越大;正偏心角时,反演出的粒径分布的Sauter平均粒径偏小。

比较图6和图7还可以得出:由于偏心距的存在,图6中随着平均粒径的增大,反演出的粒径分布及其Sauter平均粒径均较快且严重地偏离无偏心时的情况,而图7中随着平均粒径的增大,反演出的粒径分布及其Sauter平均粒径均较慢且轻微地偏离无偏心时的情况。因此可以得出:负偏心对粒径测量的影响明显大于正偏心对粒径测量的影响。

图8给出了焦距为63 mm、折射率为1.33、粒径为60µm、ξ32=60.29µm、偏心距为0.15 mm和0.07 mm时不同偏心角对粒径分布及其Sauter平均粒径的影响。可以看出:

(1)从粒径分布的角度,图8(a)在偏心距为0.15 mm、偏心角为-90°时,反演出的粒径分布呈现较明显的双峰分布,与无偏心时反演出的粒径分布有较大偏离;偏心角为0°时,反演出的粒径分布在基本保持单分散系的基础上向小粒径范围偏移;偏心角为90°时,反演出的粒径分布与0°时情况相比,偏移量增加很小;图8(b)在偏心距为0.07 mm时、除了在偏心角为-90°时呈现出微弱的双峰分布以外,其余偏心角时反演出的粒径分布与无偏心时反演出的粒径分布从图上也很难区分。

(2)从Sauter平均粒径的角度,在两种偏心距的情况下,随着偏心角绝对值的增大,反演出的粒径分布的Sauter平均粒径越加偏离无偏心时的情况。另外,与0.07 mm时相比,偏心距为0.15 mm时反演出的粒径分布的Sauter平均粒径更严重地偏离无偏心时的情况。

因此可以得出:偏心情况下,反演出的粒径分布及其Sauter平均粒径偏离的主要原因是偏心距。偏心角对粒径测量的影响要明显小于偏心距对粒径测量的影响;随着偏心角绝对值的增加,反演出的粒径分布及其Sauter平均粒径与无偏心时相比,偏离量增加得很小。

图9给出了平均粒径为60µm、ξ32=60.29µm的情况下,偏心对不同吸收性颗粒测量的影响(图6(c)给出非吸收性颗粒的情况)。可以明显地看出:

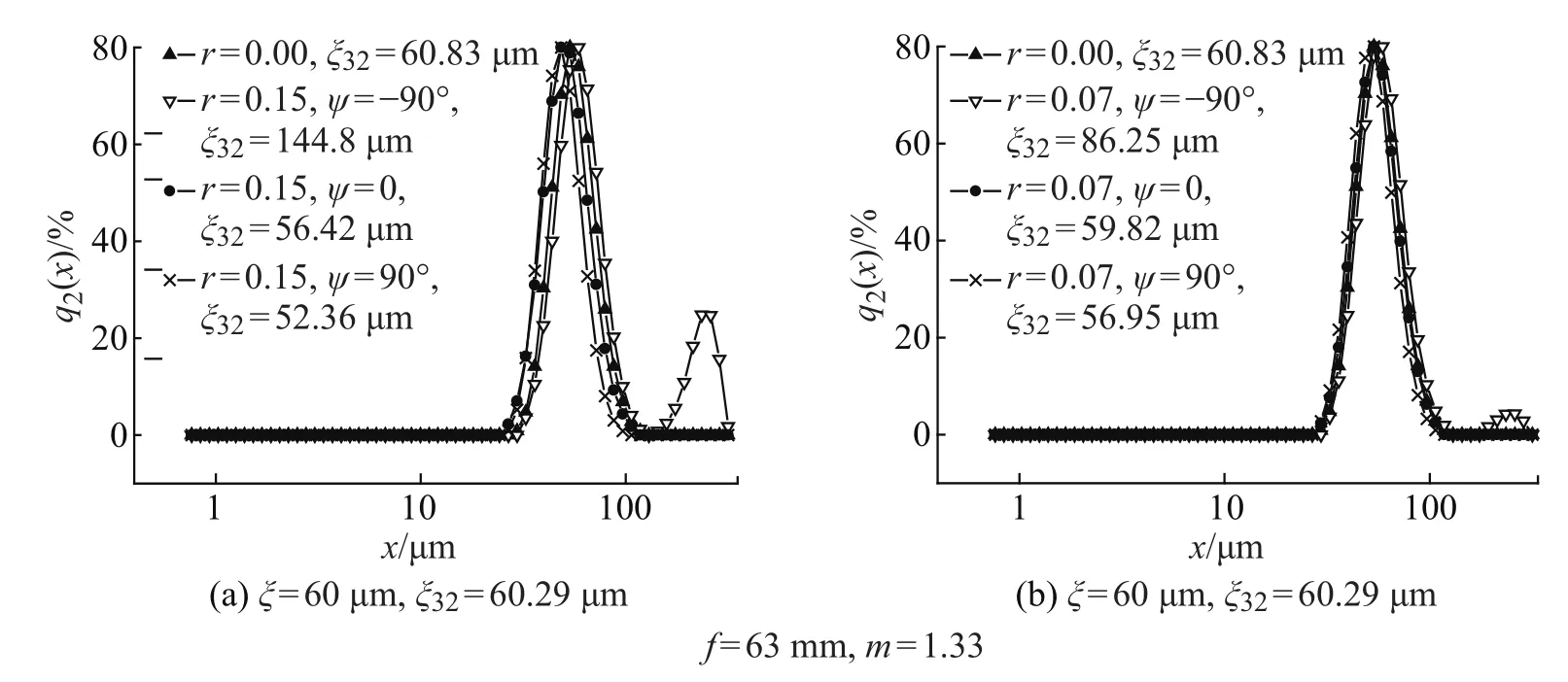
图8 不同偏心角对粒径分布的影响Fig.8 Influence of angle of eccentricity on results of measurementfor a monodisperse particle systems

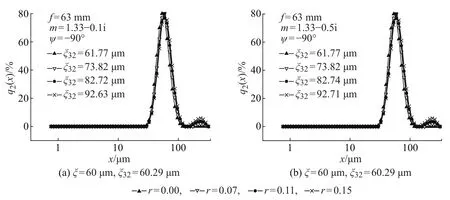
图9 偏心时颗粒吸收性对粒径分布的影响Fig.9 Influence of eccentricity on results of measurementfor transparentand absorptive particles

(1)从粒径分布角度,对于非吸收性颗粒(见图6(c)),偏心时反演出的粒径分布出现明显的双峰分布,与无偏心时反演出的粒径分布偏离较大;对于吸收性颗粒(见图9(a)、图9(b)),偏心时反演出的粒径分布只出现微小的双峰分布,与无偏心时反演出的粒径分布偏离较小。

(2)从Sauter平均粒径角度,对于非吸收性颗粒(见图6(c)),随着偏心距的增大,反演出的粒径分布的Sauter平均粒径较快且严重地偏离无偏心时的情况;对于吸收性颗粒(见图9(a)、图9(b)),随着偏心距的增大,反演出的粒径分布的Sauter平均粒径较慢且轻微地偏离无偏心时的情况。

(3)比较图9(a)和图9(b)可见,对于不同吸收能力的颗粒,偏心时反演出的粒径分布及其Sauter粒径基本相同,没有很明显的差别。

因此可以得出:偏心对吸收性颗粒测量的影响要小于对非吸收性颗粒测量的影响。

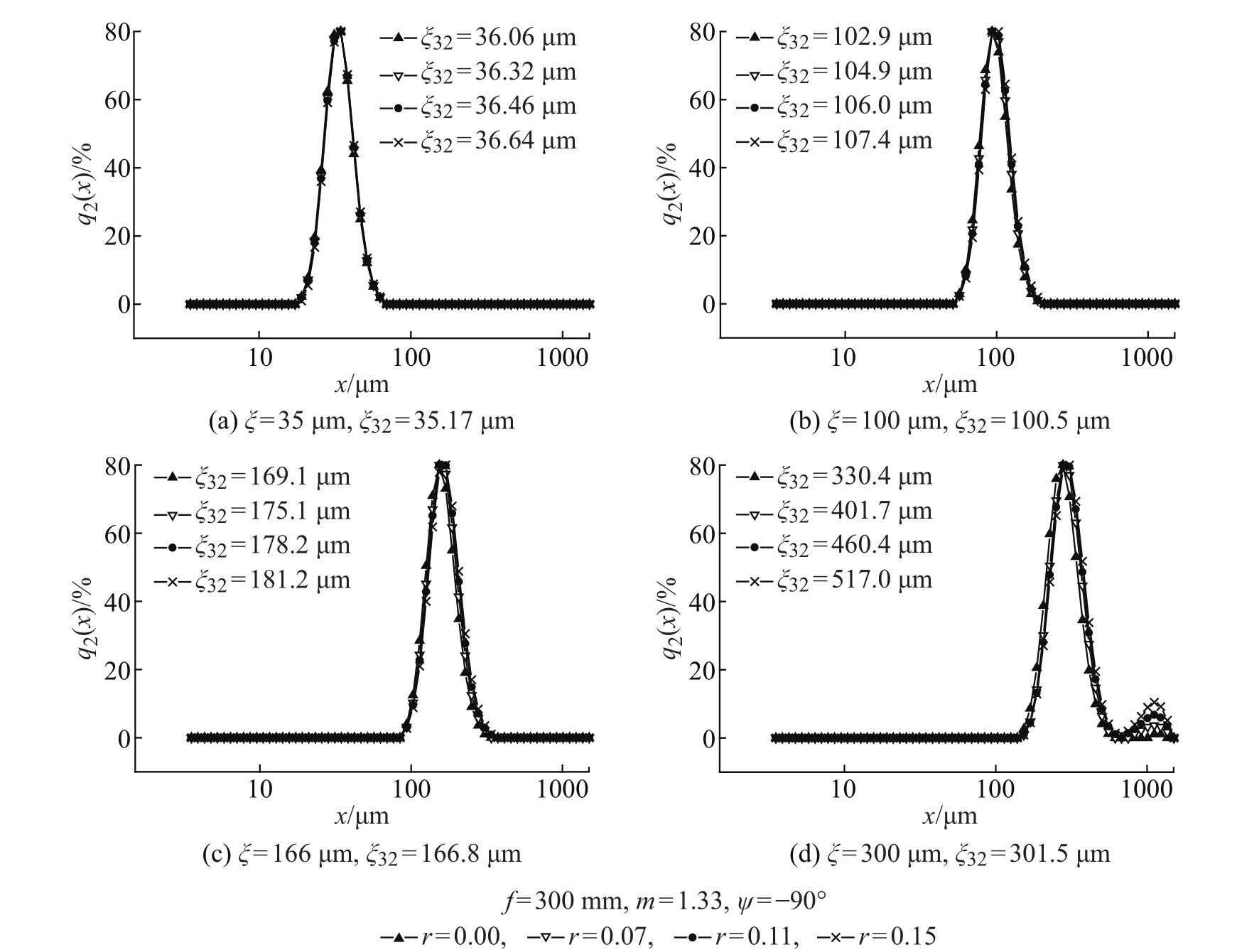
图10偏心时不同焦距对粒径分布的影响Fig.10 Influence of eccentricity on results of measurementin the case of differentfocus length

图10 给出了焦距为300 mm、折射率为1.33、偏心角为-90°时,平均粒径为35µm、100µm、166µm、300µm,ξ32为35.17µm、100.5µm、166.8µm、301.5µm的情况下,光电探测器偏心对单分散系的粒径分布及Sauter平均粒径的影响。可以看出:

(1)图10(a)、图10(b)与图6(b)、图6(d)相比,在不同焦距的粒径测量范围重叠区域,焦距越长,偏心时反演出的粒径分布及其Sauter平均粒径均越接近于无偏心时的情况。

(2)从图10中可以看出,随着平均粒径增大,偏心时反演出的粒径分布及其Sauter平均粒径越加地偏离无偏心时的情况。当颗粒处在长焦距粒径测量范围的大颗粒区时(见图10(d)),偏心时反演出的粒径分布及其Sauter平均粒径也会与无偏心时情况偏离较大。

因此可以得出:由于不同焦距测量时粒径范围有重叠区域,考虑到偏心情况,优在采用长焦距。

4 结论

在相同焦距、相同折射率和相同粒径的情况下,负偏对粒径分布及其Sauter平均粒径的影响要明显大于正偏情况下的影响。在负偏情况下,反演出的粒径分布当粒径较小时与无偏心时较接近,随着粒径的增大则较快且严重地偏离单分散系分布,当颗粒较大时则出现双峰甚至多峰分布,严重偏离无偏心时的情况;反演粒径分布的Sauter平均粒径比无偏时的情况大。在正偏情况下,反演出的粒径分布当粒径较小时与无偏心时较接近,随着粒径的增大则在基本保持单分散系分布的基础上向小颗粒方向逐渐偏移;反演出的粒径分布的Sauter平均粒径比无偏心时的情况小。

在相同焦距、相同折射率、相同粒径的情况下,偏心距或偏心角越大,反演出的粒径分布及其Sauter平均粒径越偏离无偏心的情况,但是偏心距的影响要明显大于偏心角的影响。

在相同焦距、相同折射率的情况下,偏心对大颗粒测量的影响要大于对小颗粒测量的影响。在小颗粒情况下,偏心时反演出的粒径分布及其Sauter平均粒径与无偏心时较为接近;而在大颗粒情况下,偏心时反演出的粒径分布及其Sauter平均粒径均较严重地偏离无偏心时的情况。

在相同焦距情况下,偏心对非吸收性颗粒测量的影响要大于对吸收性颗粒测量的影响。特别在较大颗粒情况下,非吸收性颗粒的偏心时反演出的粒径分布及其Sauter平均粒径较严重地偏离无偏心时的情况,而吸收性颗粒的偏心时反演出的粒径分布及其Sauter平均粒径较轻微地偏离无偏心时的情况。

在不同焦距测量范围有重叠区域情况下,长焦距对颗粒测量的影响要小于短焦距对颗粒测量的影响。在利用短焦距测量较大颗粒时,偏心时反演出的粒径分布及其Sauter平均粒径较严重地偏离无偏心时的情况,而长焦距测量相同粒径颗粒时,偏心时反演出的粒径分布及其Sauter平均粒径与无偏心时情况较接近。因此,在利用基于Mie理论的小角前向散射激光测粒技术时,为了最大幅度地减小偏心导致的影响,在减小偏心距和偏心角的前提下,尽可能地使偏心点处于正偏心的区域内。并且,在焦距测量范围允许的情况下,尽量选用长焦距来测量颗粒。

需要说明的是,由于光靶孔径的限制使得最大偏心距离不会超过0.15 mm。在如此小的距离内,很难把光电探测元件中心置于某个确定的偏心位置,很难利用实验来验证偏心的影响。因此,本文仅通过模拟计算研究在小角前向散射激光测粒技术中偏心对颗粒粒径分布测量的影响。

[1]王乃宁.颗粒粒径的光学测量技术及其应用[M].北京:原子能出版社,2000.

[2]WANG N N,SHEN J Q.A study of the influence of misalignmenton measuring results for laser particle analyzers [J].Part.Part.Syst.Charact.,1998,15(3):122-126.

[3]VAN DE HURST H C.Lightscattering by smallparticles [M].New York:Dover Publications,1981.

[4]HIRLEMAM E D.Optimal scaling of inverse fraunhofer diffraction particle sizing problem:the linear system pro-duced by quadrature[J].Part.Charact.,1987,4:128-133.

[5]SHEN JQ,SUMX,LIJF.A new algorithm ofrelaxation method for particle analysis from forward scattering light [J].China Particuology,2006,4(1):13-19.

[6]CHAHINE M T.Determination of the temperature profile in an atmosphere from its outgoing radiance[J].J.Optic Soc.Amer.,1968,58(12):1634-1637.

The Influence ofthe Eccentricity ofthe Small-Angle Forward Scattering Laser Particle Sizer

WANG Yu
(Schoolof Science,ShanghaiSecond Polytechnic University,Shanghai201209,P.R.China)

Based on the classical Mie scattering theory,the technology of the small-angle forward scattering laser particle sizer has been widely used in various fields.In order to ensure the accuracy of the measured scattering light energy distribution and the particle size distribution,the center of photoelectric detection unit and incident optical axis must strictly centring.However itis very difficult in actualmeasurement.Based on the Mie scattering theory,the simulations on the influence of the bad centring(mainly eccentric)are shown,and the results are analyzed.

forward scattering;particle sizing;Mie scattering theory;the eccentricity;simulation

O436.2

A

1001-4543(2013)04-0301-10

2013-06-03;

2013-11-05

王玉(1964–),女,辽宁人,副教授,学士,主要研究方向为力学、电磁学,电子邮箱wangyu@sspu.edu.cn。