运用类比法进行离散数学教学探究①

李世群，袁梓瀚，马千里

(1.湖南科技大学数学与计算科学学，湖南湘潭411201;2.华南理工大学计算机科学与工程学院，广东广州510006)

“所谓类比法是指研究和认识新对象时联想和它类似的已知对象，并根据新对象与已知对象之间部分属性的相似性得到其他属性也相似的推断，从而导致发现新规律的思维方法，其整个思维过程是以“联想”为前提，以相似性为向导，以发现新规律为目的。

类比的对象是同一层次上的两类不同事物，一方面，在同一层次上是保证类比的可行性，另一方面，这两种不同类事物之间具有相似性。两个事物之间的相似性是类比能够进行过渡的环节或逻辑中介，没有相似性就无法进行类比。类比的最大价值就是在两类不同事物之间建立起由已知到未知的桥梁。

目前我国的教育管理部门虽然都开始重视课堂教学改革，但由于教师的科研任务繁重等原因，填鸭式教学方式充斥课堂，教师照本宣科的现象还很严重，他们忽视了学生的自主学习，忽视了数学学习过程中猜测的力量，忽视了学生数学思维能力的培养。导致了大学生数学能力发展不全面，缺乏创新精神与实践能力。大学教师在数学课堂教学中运用类比法进行教学，合理选择学生熟知的类比对象，分析概括类比对象与新授知识的共同本质，不仅可以使学生容易理解新知识，而且能够极大激发学生的学习兴趣，使学生掌握自主学习的方法，大面积提高数学课堂教学质量，更有利于学生数学思维能力的培养。

一 用类比法进行数学课堂教学的现实意义

(一)用类比法教学有利于培养学生数学思维

著名教育家布鲁纳认为:“所谓知识是过程，，不是结果”，现在对大学进行数学教学的目的，不是只教会学生学会什么，更重要的是使学生看到学习这些知识的发生及推演过程，培养学生的数学思维能力，这种思维过程的学习比结果的学习更重要。

运用类比法进行数学教学，能够更好地揭示相关数学知识之间的内在关联，有利于学生从整体上理解数学，构建数学认知结构.同时，由于“类比是合情推理的一种思维形式，即是由两个或两类思考对象在某些属性上的相同或相似，从而推出它们在另一属性上也相同或相似的一种推理方法”［1］，因此，这种这种思维推理方法对于学生进行自主的数学学习及其他生产生活知识的学习都是非常重要的，用类比法进行教学，学生不仅掌握了数学专业知识，还学会了如何用类比思维思考问题的方法。

(二)用类比法教学有利于学生接受新知识

在数学教学中，许多概念对于初学者显得比较抽象，学生难以接受，而这些数学概念之间往往在特征、结构方面有相似之处，“类比法恰好是将已有的知识和新的学习活动联系起来的一种重要方法”［2］，所以，运用类比方法进行新概念的教学时，通过与熟悉概念的类比，就能帮助学生去认识和理解新概念，建立起适当的心理表征，可以使学生温故而知新、完成新知识的学习。如在离散数学教学中，数理逻辑中的命题公式、公式的真值指派、谓词等概念对学生会感到抽象和陌生，由于函数对于每个学生都是很熟悉的是中学学过的知识，我们选择函数作为类比对象，学生立刻感到有一种已经熟悉而亲切的感觉，他们会发现新概念的特征与过去的已知的概念相似，思维马上就会处于一个兴奋点，教师只要把新的概念与对应的函数中的已有的对象联系起来进行类比，新概念就成为容易理解的和容易把握的。

(三)用类比法教学有利于学生掌握学习程序

由于类比推理是一种开放性的思维过程，它为学生提供了一处非常开阔而且多彩的思维境界，按事物发展的阶段进行层次性类比，有助于我们加深对事物发展一般规律的认识，开拓知识体系.可以使我们摆脱在学习中完全受命于人(课本、教师)的被动学习方式，使学生掌握学习程序，把握学习规律，将学习的主动权掌握在学生自己手里，比如，在进行数理逻辑的一阶逻辑的教学时，由于前一阶段学生已经学习过命题逻辑，此时将命题逻辑作为类比对象，引导学生回顾命题逻辑的发展阶段:

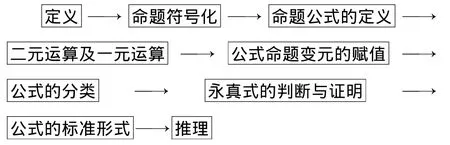
类比命题逻辑的程序，引导学生猜想可得到与命题逻辑完全对应的一阶逻辑的学习程序。

(四)用类比法教学有利于激发学生探索和创新

“在科学研究中，人们利用因果类比、数学类比、模型类比，使其充分显示了强大的发现、创造功能，例如，在近代科学史上，开卜勒受几何图形类似的启发，提出行星运动三定律;麦克斯韦也曾得益于类比，建立了麦克斯韦电磁理”［3］。

在大学阶段的学生的思维已经发展到了一个更加活跃、推理能力更强的阶段，学生具有很强的主动性和独立性，因此数学教学过程中运用类比法教学，可以使学生学习运用类比思维进行探索，有利于学生进行探索和创新，达到培养创新型人才的目的。

(五)有利于学生终身学习

现代社会经济发展的需要，决定了每个人都要终身进行学习，这种终身学习就要靠自己学会合情推理，而类比思维方法正是合情推理的一种重要思维方法。类比思想方法不仅可以用到数学学习中，而且用到日常生活、生产等各方面，现代社会要求每个公民应具有类比思维方法进行实验观察、获取信息、数据处理、合情推理、预测猜想、探究创造，等等［4］。运用类比法进行教学正是培养了学生的这种思维。

二 用类比法教学的策略

(1)选择恰当的类比对象

要运用类比法进行数学教学，首先是要选择恰当的类比对象。要使类比对象的选择恰当，一是要研究学生的数学现实，了解学生原有的数学知识结构，使得选择的对象符合学生的数学现实［5］。学生的数学现实与数学理论(即数学教学目标)之间存在一个“中间地带”，相当于维果斯基所提出的“最近发展区”，“采用化归、迁移、类比、同化等手段对“数学现实”进行连续不断地“建构”已是数学教师运用娴熟、学生也予以普遍接受的教学方式“［6］.同样的内容对于不同专业和不同年级的学生选择的类比对象也会有所不同。二是要选择相似度高的类比对象，使得类比对象具有与所要学习的对象的本质特征基本相同。例如，以李世群、马千里的《离散数学》［7］为教材的在命题逻辑教学中，要使学生理解命题公式、真值指派、真值表、公式的类型及公式的等价，我们选择类比对象——函数，由于函数对于每个专业每个年级的学生都是很熟悉的对象，将这些教学内容进行类比函数中对应的内容，便可以得到新概念的结构，当然，命题逻辑中每一个具体概念还要在函数这个大的类比对象中再次选择具体的类比对象，我们将具体类比对象与原对象列成下面对照表:

(2)把好抽象与提炼关

恰当地选择好一个学生熟悉的类比对象后，就要引导学生分析新概念的特征。抽象提炼的过程大致可分三个阶段，“第一阶段是从一系列思维过程搜索出另一个或一类具体的类比对象，其次，对已确定的、具体的类比对象进行科学加工，对类比对象的本质和属性加以概括的提炼，最后，在创造对象和类比对象之间找到共同点或相似点，实现创造对象和类比对象的抽象统一”［4］，这个过程也是类比教学的关键点，通过分析提炼和类比猜想，会很快达到问题的实质，而且要符合学生认识水平，便于学生接受和理解。如在进行两个公式A与B等价A⇔B当且仅当A↔B为永真式的教学过程中，学生往往不理解，而且还容易将概念A↔B与A⇔B混淆，我们选择函数f=g作为类比对象，将运算符号“↔”与减法符号“－”类比;永真式与常函数0进行类比，然后分析提炼，找出A⇔B与f=g的共同点:

f=g当且仅当f－g为常函数0;

A⇔B当且仅当A↔B为永真式(本质类似常函数);

学生很快就理解并掌握了。

(3)用类比法进行复习课教学

复习课的一个任务之一是要帮助学生完成一个阶段的已学知识的整体结构的认识，其中包括认识知识之间的联系，相似之处，帮助学生强化已学知识，而这种强化过程又不能做简单的重复，要达到这个目标，用类比法教学是一个非常有效的方法，一方面引导学生在两个已学的新知识的结构和性质之间类比，用类比法将两种对象的本质和属性加以概括提炼，在新对象和类比对象之间找到共同点或相似点，实现创造对象和类比对象的抽象统一，帮助学生建立新知识之间的联系，还可以帮助学生减轻记忆负担。另一方面将新知识和以前(包括中学学过的)知识之间进行类比，能够帮助学生强化对这一阶段新知识的认识。

如学习欧拉定理以后，将欧拉定理与握手定理进行结构性类比，即将握手定理:“各顶点的度数之和等于边数的两倍”类比欧拉定理:“平面图的所有面次数之和等于边数的两倍”。又如在二元关系的复习总结课的教学中，将偏序关系、相容关系与等价关系进行类比，对三个条件进行差异性类比:等价关系具有反身性，对称性，传递性;而偏序关系具有反身性，反对称性，传递性，它们仅第二个性质存在差异;而在集合这一章的复习课教学中，将集合的交、并、求余等运算律与数理逻辑中的合取、析取、非等运算律进行类比，通过这种类比，强化了关于这些知识的认识。

(4)要注意差异性

用类比法进行教学时要提醒以下几点:一是两个可比对象性质并非完全一样，在教学中，要让学生明确它们哪些方面可以类比，哪些方面不可类比.二是只有本质相同或相似的事物才能进行类比.如果把仅仅形式上相似而本质上都不相同的事物类比，就会造成错误.三是要让学生清楚类比的结果并非完全可靠，只是形成猜想的一种思维方法，猜想的结果是否正确还需证明与验证，必要时还需对猜想进行修正。

如将n元命题公式类比学生已知的n元函数，它们相同的函数特征是有自变量和因变量，而差别在于n元命题公式的自变量的定义域为{0，1}n，值域属于{0，1}，而一般n元函数的定义域和值域是实数域R的连续子集。

［1］汤慧龙.关于学生“数学现实”的研究［J］.数学教育学报，2004(2).

［2］邓理进.试论数学类比教学的作用［J］.常州师专学报，2002(6).

［3］仲秀英.波利亚的类比思想与数学课程改革［J］.重庆师范学院学报(自然科学版)，2003.

［4］张奠宙.关于“现实数学”和“数学现实”［J］.数学教育学报，2008(2).

［5］丁 荃.类比是一种重要的创造性思维方法［J］.科学技术与辩证法，2000(2).

［6］孙杰远.类比:比较教育研究及其创新的思维本质［J］.西南师范大学学报(人文社科版)，2005.

［7］李世群，马千里.离散数学［M］.天津:天津大学出版社，2010(6).