基于人工蜂群算法的波达方向和多普勒频率联合估计

张志成，林 君，石要武，孙晓东

（1.吉林大学 通信工程学院，长春 130012；2.吉林大学 仪器科学与电气工程学院，长春 130061）

0 引 言

近年来，波达方向（DOA）和多普勒频率联合估计技术在多个领域引起了广泛的关注和研究，但估计精度、运算量和参数配对等问题一直是DOA和多普勒频率联合估计算法的主要制约因素。现有的DOA和多普勒频率联合估计方法大多由一维的子空间分解类算法发展而来。文献［1－5］基于ESPRIT算法实现了对DOA和多普勒频率的联合估计，虽然其中一些算法实现了参数的自动配对，但其无法达到最佳的估计精度，且只适用于均匀线阵的情况，在低信噪比或采样快拍数较小的条件下，其参数估计性能较差。文献［6］提出了一种简单有效的频率－空间－频率（FSF）的树状结构，利用三次一维 MUSIC／ESPRIT算法实现了对DOA和多普勒频率的联合估计，且参数可以自动配对，但该方法得到的估计结果依然不是最优估计。最大似然方法是一个性能优良的最优估计方法，但其求解过程需要进行非线性的多维搜索，大大增加了算法的复杂度。文献［7］利用最大似然方法实现了DOA和多普勒频率的联合估计，并将多维最优化问题转换成多个一维最优化问题，简化了计算，但其估计误差较大且需要额外的参数配对运算。文献［8－9］利用重要性采样技术降低了求解似然函数最大值的计算量，并实现了DOA和多普勒频率的参数自动配对，但其需要根据信噪比的不同而不断调整重要性采样函数，且算法所需要的控制参数较多，不利于实际应用。

本文将状态空间模型和最大似然方法相结合，提出了一种基于最大似然方法的DOA和多普勒频率联合估计算法。利用状态空间模型能够分析和处理时变系统的特性，将待估计的参数转换到状态空间模型的系统矩阵中，利用Hankel矩阵构造数据协方差矩阵来抑制噪声，进而通过最大似然方法得到信号角度和多普勒频率的估计值，并利用人工蜂群算法对似然函数求解进行优化。该方法可得到渐近无偏的参数估计，参数能够自动配对，且大大减小了最大似然方法的计算量。

1 角度和多普勒频率联合估计

1.1 接收数据模型

假设接收阵列为具有M个阵元的线列阵，以阵列的第一个阵元作为基准，阵元间距为（0，d1，…，dM－1），共有P个远场窄带信号源，其中M ＞P，设波达方向为 （θ1，θ2，…，θP），且假设所有的信号都具有相同的载频，则阵列接收到的信号可写为

式中:v（t）为复噪声向量，假设为高斯白噪声；sp（t）为信号的复包络，可写成sp（t）＝αpej2πfpt，其中αp为复幅度，fp为第p个信号源的多普勒频率；θp为第p个信号源的到达角度；a（θp）表示θp的方向向量，其定义为

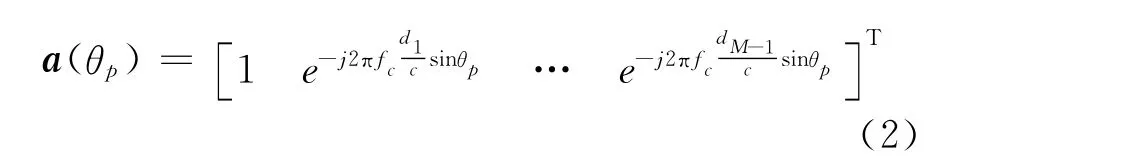
式中:fc为信号的载频；c为信号传播速度。

利用归一化频率来描述多普勒频率，式（1）可写成下列矩阵形式

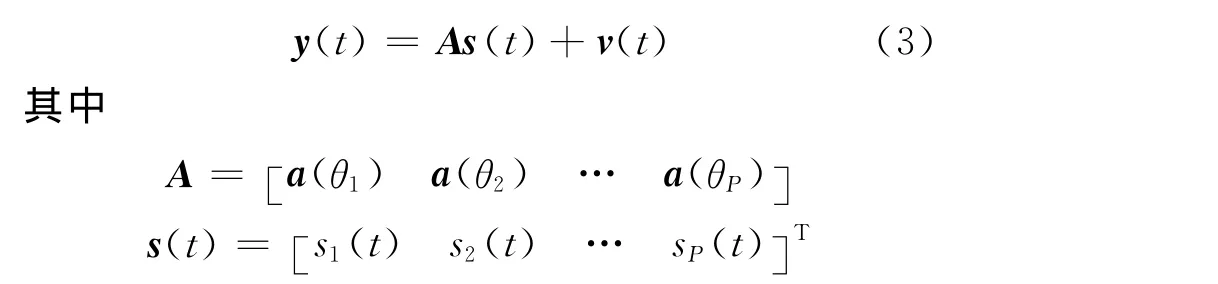
由此可以得到如下形式的状态空间模型

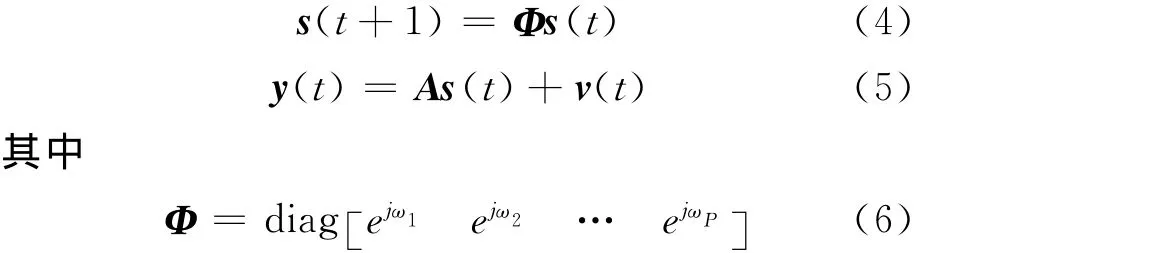
式中:ωp＝2πfp。

1.2 信号参数的估计

为了对噪声进行抑制，并能够准确地对波达方向和多普勒频率进行估计，本文方法从构造Hankel矩阵开始。

定义阵列接收数据和噪声数据Hankel矩阵如下

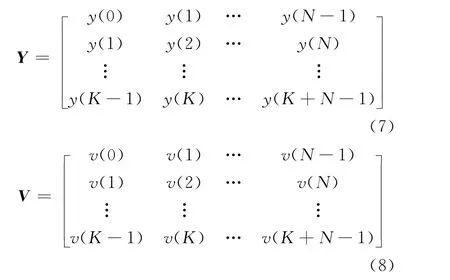
式中:N、K分别为构成Hankel矩阵的行数和列数；N＋K为采样快拍数。

定义信号采样向量为

则式（4）（5）的状态空间模型可以被写成

式中:ΓK为广义可观测矩阵，其具有如下的形式

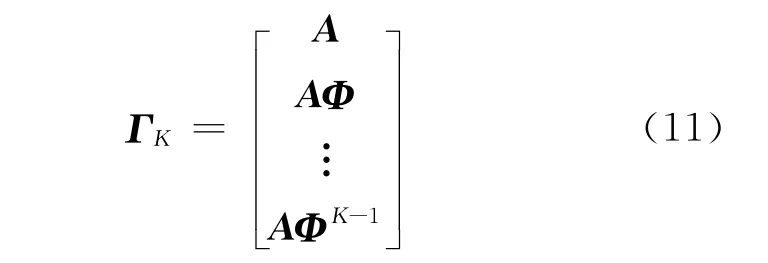
式（10）具有与阵列接收数据矩阵相同的形式，其可被定义为一种经过扩展的阵列接收数据矩阵。Hankel矩阵Y可表示为采样快拍数为N的阵列接收数据矩阵，其每一列可被视作一次采样，则式（10）可写作

式中:ΓK已包含了待估计的角度和多普勒频率信息。

取观测数据Y（n）的对数似然函数:

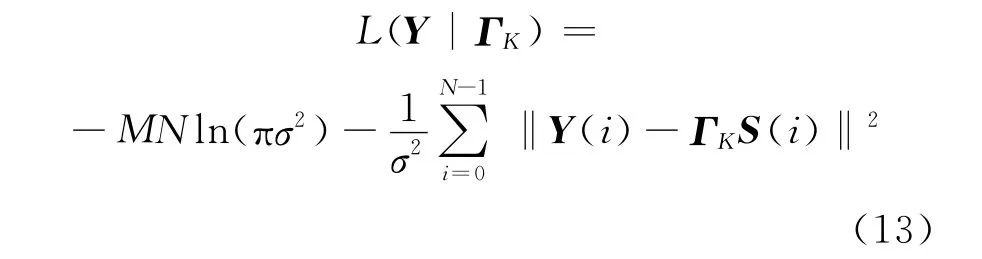
式（13）是一个关于未知参量θ、ω、σ2和S（n）的非线性函数，其中未知参量σ2和S（n）的确定性最大似然估计分别为

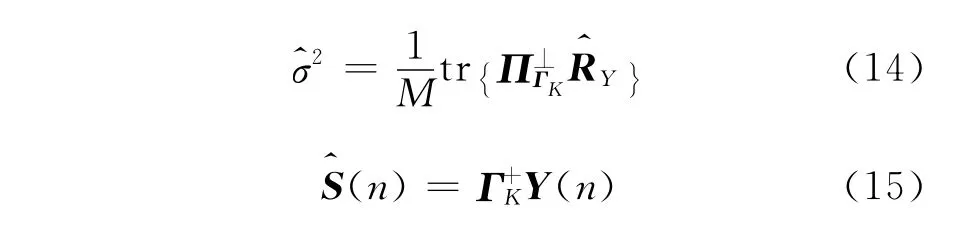
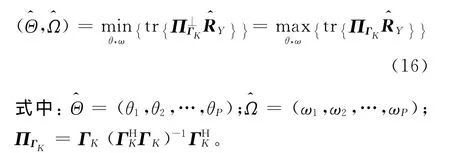
式（16）的求解需要通过非线性多维搜索实现，由于ΓK是包含DOA和多普勒频率信息的已知结构矩阵，因此在搜索过程中可实现DOA和多普勒频率的自动配对。

2 似然函数的全局优化

2.1 人工蜂群算法

人工蜂群算法（Artificial bee colony alogrithm，ABCA）是一种基于群体智能的启发式搜索算法［10－11］，它模仿自然界中的蜂群总能寻找到最好的蜜源这种行为，具有控制参数少、易于实现、计算简洁等优点，在求解组合优化、多峰函数求极值等问题中显现出了优良的特性。

人工蜂群算法将蜜蜂种群分为三部分:采蜜蜂、待工蜂和侦察蜂。对于函数优化问题，蜂群中的每个采蜜蜂对应着一组解。开始搜索时，由侦察蜂随机搜索解空间内的解，然后侦察蜂变成采蜜蜂，将所搜索到的解按照由好到坏（根据适应度函数的高低）排序，并对其邻域进行搜索。如果邻域搜索到的解优于现有的最优解，则替换现有的解，反之则保持现有的解不变。在所有的采蜜蜂都完成邻域搜索后，采蜜蜂将所搜索到的解信息与待工蜂共享。待工蜂根据一定的概率选择采蜜蜂进行邻域搜索，适应度高的采蜜蜂吸引更多的待工蜂。待工蜂搜索到的邻域解与采蜜蜂的现有最优解进行比较，如果优于现有最优解则替换该解；反之则保持现有解不变并继续进行邻域搜索。邻域搜索不能无限制地进行，当搜索达到一定次数但搜到的解仍没有改善时，这组解将被放弃，所对应的采蜜蜂变成侦察蜂重新开始随机搜索一组新的解。

在人工蜂群算法中，三种不同蜜蜂扮演了各自不同的角色。采蜜蜂用来保持优良的解集；待工蜂用来加快全局最优化的收敛速度；侦察蜂有助于跳出局部最优解。整个蜂群分工协作，直到找到全局最优解。

2.2 基于人工蜂群算法的似然函数优化

假设蜂群总数为LS，其中采蜜蜂和待工蜂数量分别为LE和LO（令LE＝LO），搜索维数为2P，角度和多普勒频率的搜索范围分别为（－90°，90°） 和 （－π，π）。每一组解（i＝1，2，…，LE）为一个2P维的向量，所有的初始化解均由侦察蜂按照下面的公式进行随机搜索

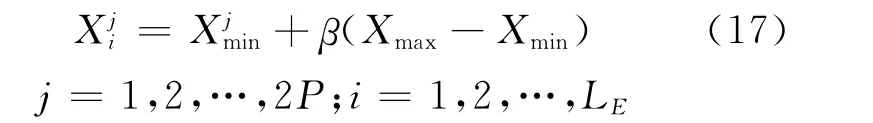
式中:Xmin和Xmax分别为搜索范围的最小值和最大值；β为在（0，1）范围内的随机数。由此可以得到初始解集X2P。

侦察蜂在完成初始化搜索后转变为采蜜蜂，并进行邻域搜索。邻域搜索可按照下式进行:

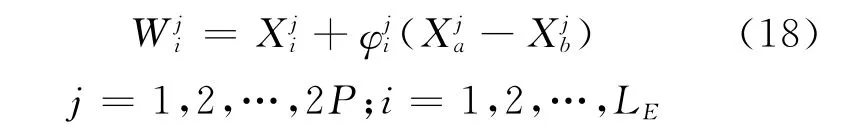
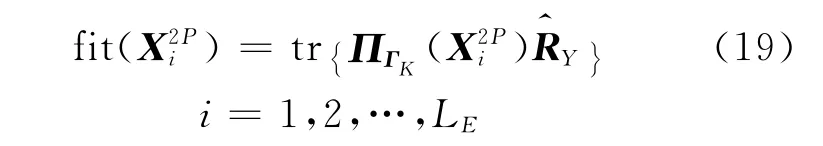
式中:ca和cb为在（0，1）范围内的概率系数，其取值大小将决定待工蜂选择变为采蜜蜂的概率。适应度高的解将吸引更多的待工蜂，适应度低的解将吸引少量的待工蜂或者根本吸引不到待工蜂。

如果某一组解经过一定次数的邻域搜索仍然无法提高其适应度，该组解将被放弃，其所对应的采蜜蜂将转变为侦察蜂重新随机搜索一组新的解。

按照以上的步骤进行迭代，最终将得到适应度最高的一组解，该组解即为使似然函数最大的一组角度和多普勒频率的估计值。

2.3 计算量分析

最大似然算法需要通过多维网格搜索实现，其计算复杂度为O｛［（θmax－ θmin）（ωmax－。其中，（θmin，θmax）和Δθ分别为角度搜索范围和搜索步长；（ωmin，ωmax）和Δω分别为频率搜索范围和搜索步长。利用人工蜂群算法实现参数估计的计算复杂度约为O（2PLSIN＋LS）。其中，LS和IN分别为蜂群数量和迭代次数。

表1给出了两种算法在不同信源数情况下的计算量比较。其中，角度搜索范围和搜索步长分别选取 （－90°，90°） 和0.5°；频率搜索范围和搜索步长分别选取 （－π，π）和0.01rad；蜂群数量和迭代次数分别选取100和200。

表1 网格搜索与人工蜂群算法计算量比较Table 1 Computation load comparison of grid search and artificial bee colony algorithm

由表1可以看出，人工蜂群算法的计算量远小于网格搜索，特别是当信源数增加时，网格搜索的计算量呈指数增长，而人工蜂群算法的计算量呈线性增长。当信源数较多时，人工蜂群算法的优势更加明显。

3 仿真验证

仿真实验采用线列阵，阵元数M＝10，采样快拍数为100。在高斯白噪声背景下，采用100次独立Monte Carlo实验，以如下均方根误差（RMSE）作为衡量算法性能的标准:

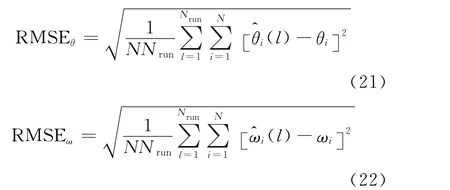
实验1 分别采用人工蜂群算法、微分进化算法和遗传算法对似然函数进行优化求解。由于种群数量和迭代次数是决定群体智能优化算法的关键参数，分别选取相同的种群数量和迭代次数可使以上三种优化算法的计算量大致相等。因此，选取种群数量为50，迭代次数为100次。仿真实验取入射信号数P＝2，入射信号的入射角度分别为（20°，30°），入射信号的归一化多普勒频率分别为（0.7，0.9）。

图1和图2分别给出了三种算法在信噪比变化时DOA估计和多普勒频率估计的均方根误差的变化。从图1、图2中可看出，人工蜂群算法能够很好地实现对似然函数的优化，每次优化均可以找到似然函数的最大值，具有很好的鲁棒性。对于微分进化算法和遗传算法，由于种群数量和迭代次数的限制，算法无法保证每次都能找到全局最优解，要想获得更好的函数优化性能，必须增加种群数量和迭代次数，这将大大增加算法的计算量。由此可见，人工蜂群算法可以用较小的计算量实现对似然函数较精确的求解。

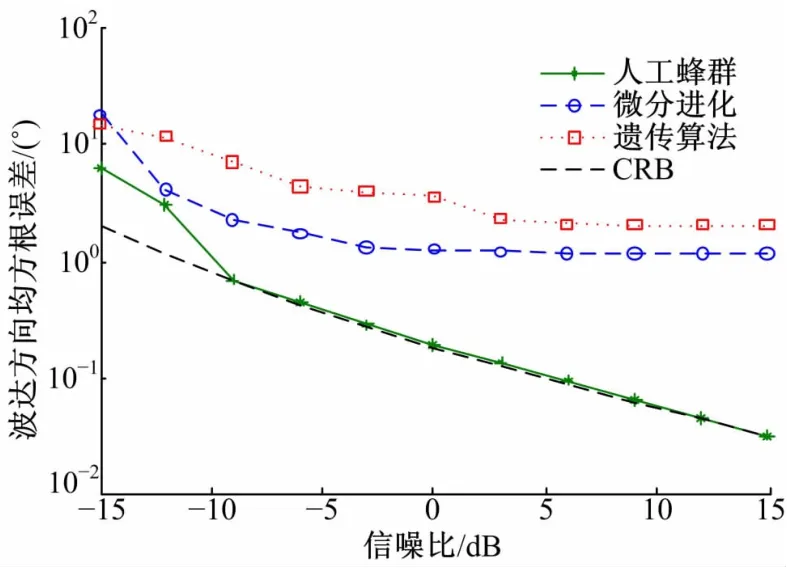
图1 不同优化算法DOA估计均方根误差比较Fig.1 RMSE of DOA estimation compared with other optimization methods

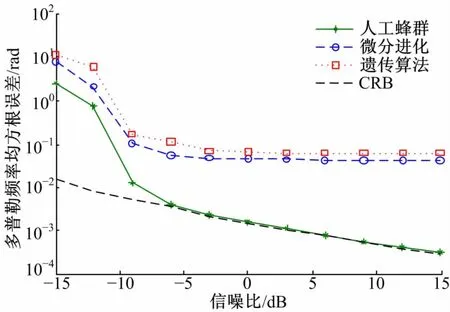
图2 不同优化算法频率估计均方根误差比较Fig.2 RMSE of frequency estimation compared with other optimization methods

实验2 选取两个较具代表性的DOA和多普勒频率联合估计算法:JAFE［5］算法和 FSFMUSIC［6］算法，与本文算法进行比较。由于以上两种算法只适用于均匀线阵，故采用均匀线阵对算法进行仿真。考虑入射信号数P＝3的情况，信号源的波达方向分别为（20°，30°，40°），信号源的归一化多普勒频率分别为（0.7，0.9，1）。图3和图4分别给出了三种算法在信噪比变化时DOA估计和多普勒频率估计的均方根误差的变化。从图3、图4中可以看出，本文算法的估计性能优于其他两种算法，尤其在低信噪比下，本文算法能够更早地贴近克拉美罗界。这主要得益于本文所使用的最大似然方法可得到渐近无偏的参数估计。

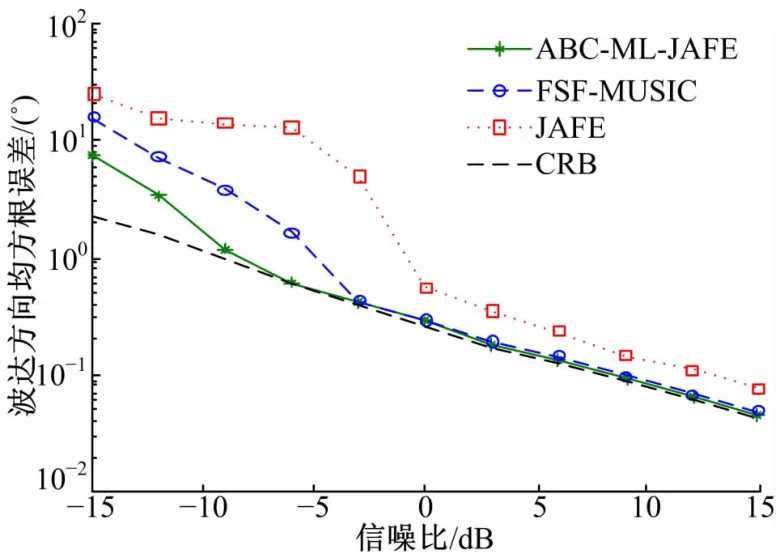
图3 不同联合估计算法DOA估计均方根误差比较Fig.3 RMSE of DOA estimation compared with other joint estimation methods

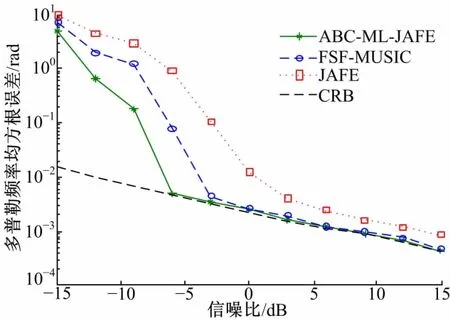
图4 不同联合估计算法频率估计均方根误差比较Fig.4 RMSE of frequency estimation compared with other joint estimation methods

实验3 考虑三个入射信号源中的两个信源参数比较接近的情况。信源参数选择如表2所示，取SNR＝0dB，对JAFE算法、FSF－MUSIC算法和本文算法的估计性能进行比较。由表2可见，本文算法能够比较准确地区分出各个信源的波达方向和多普勒频率信息，而其他两种算法的参数估计性能均受到了不同程度的影响，不能够准确分辨出参数比较接近的信号源。

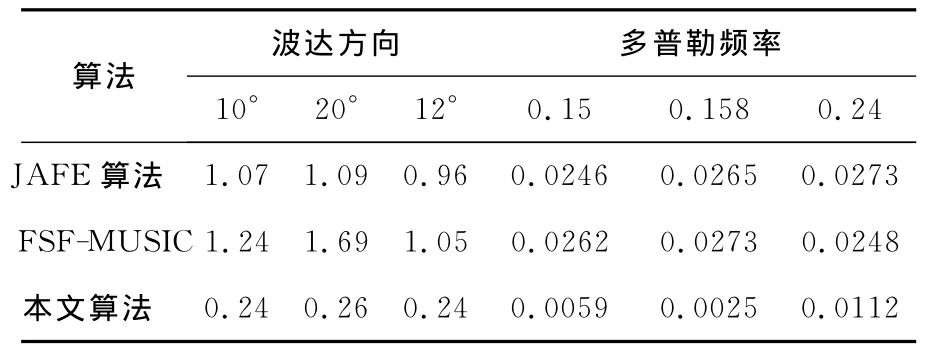
表2 信号参数较接近时的RMSETable 2 RMSE when parameters are close

4 结束语

针对波达方向和多普勒频率联合估计问题，将人工蜂群算法与最大似然估计相结合，提出了一种基于人工蜂群算法的DOA和多普勒频率联合估计方法。该方法利用状态空间模型将所要估计的参数转换到广义可观测矩阵中，再通过最大似然方法得到信号到达角和多普勒频率的估计。由于求解似然函数计算量巨大，本文将人工蜂群算法应用于似然函数的优化求解中，大大减小了算法的计算量。与其他DOA和多普勒频率联合估计算法相比，本文方法具有估计精度高、控制参数少、鲁棒性好、参数自动配对等特点，且在低信噪比和小样本下依然能够得到较满意的估计结果。

［1］Haardt M，Nossek J A.3－D unitary ESPRIT for joint 2－D angle and carrier estimation［C］∥IEEE International Conference on Acoustics，Speech and Signal Processing，Munich，1997.

［2］Lemma A N，van der Veen A J，Deprettere E F.Joint angle－frequency estimation using multi－resolution ESPRIT［C］∥IEEE International Conference on Acoustics，Speech and Signal Processing，Seattle，1998.

［3］Viberg M，Stoica P.A computationally efficient method for joint direction finding and frequency estimation in colored noise［C］∥The Thirty－Second Asilomar Conference on Signal，Systems and Computers，Pacific Grove，1998.

［4］Lemma A N，van der Veen A J，Deprettere E F.A－nalysis of ESPRIT based joint angle－frequency estimation［C］∥IEEE International Conference on A－coustics，Speech and Signal Processing，Istanbul，2000.

［5］Lemma A N，van der Veen A J，Deprettere E F.Analysis of joint angle－frequency estimation using ESPRIT［J］.IEEE Transactions on Signal Processing，2003，51（5）:1264－1283.

［6］Lin Jen－der，Fang Wen－hsien，Wang Yung－yi，et al.FSF MUSIC for joint DOA and frequency estimation and its performance analysis［J］.IEEE Transactions on Signal Processing，2006，54（12）:4529－4542.

［7］Atheley F.Asymptotically decoupled angle－frequency estimation with sensor arrays［C］∥The Thirtythird Asilomar Conference on Signal，Systems and Computers，Pacific Grove，1999.

［8］王惠刚，刘强.多普勒方位联合估计的蒙特卡洛算法［J］.电子学报，2009，37（9）:1965－1970.Wang Hui－gang，Liu Qiang.A Monte Carlo method for joint estimation of Dopplers and DOAs［J］.Acta Electronica Sinica，2009，37（9）:1965－1970.

［9］Wang Hui－gang，Steven Key.Maximum likelihood angle－Doppler estimator using importance sampling［J］.IEEE Transactions on Aerospace and Electronics Systems，2010，46（2）:610－622.

［10］Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization:artificial bee colony （ABC）algorithm［J］.Journal of Global Optimization，2007，39（3）:459－471.

［11］Karaboga D，Basturk B.On the performance of artificial bee colony（ABC）algorithm［J］.Applied Soft Computing，2008，8（1）:687－697.