基于流固耦合的冲焊型液力变矩器焊接强度分析
2013-08-16马文星卢秀泉
谭 越,马文星,卢秀泉
(1.吉林大学 汽车仿真与控制国家重点实验室,长春 130022;2.吉林大学 机械科学与工程学院,长春 130022)
0 引 言
液力自动变速器(AT)是目前及未来一段时间内车辆自动变速器中市场占有率最高的产品。冲焊型液力变矩器是液力自动变速器(AT)的核心部件。国外轿车冲焊型液力变矩器已成为研究热点,美国、韩国、日本等国家的汽车企业和高校的研究机构都投入了大量的人力物力进行冲焊型液力变矩器研究[1-3]。此种变矩器的设计和制造难度较大,其焊接结构的可靠性将直接影响变矩器的工作性能并对整个传动系的运转安全有重大影响。因此在设计时应着重对冲焊型液力变矩器焊接叶轮强度进行计算和分析。
目前国内对液力变矩器强度和结构优化的研究主要以铸造型为主,北京理工大学魏巍等[4]对液力变矩器叶片进行单向FSI强度分析,得到了叶片的变形和应力分布状态;闫清东等[5]采用周期性模型对大功率液力变矩器叶轮的FSI进行研究,为叶轮强度分析提供一种较为有效的方法。此外,同济大学陆忠东等[6]对冲焊型液力变矩器叶片的FSI作用进行了数值模拟,并对涡轮叶片结构进行了优化设计。
为了更准确地计算冲焊型液力变矩器焊接强度问题,本文基于单向FSI的方法,对某型冲焊型液力变矩器叶轮耦合系统采用整体离散和整体求解的方法进行焊接强度分析。
1 单向流固耦合分析方法
单向FSI是在固体的变形微小、忽略其对流体影响的情况下,只考虑流体应力对结构的作用[7]。单向FSI分析流程如图1所示。流场的CFD数值仿真和结构的FEA分析求解在时间上是两个相对独立的过程。CFD计算结果中耦合面上的压力值通过网格映射转化为相应的结构载荷施加到结构的耦合面上,从而进行结构的有限元计算[8]。
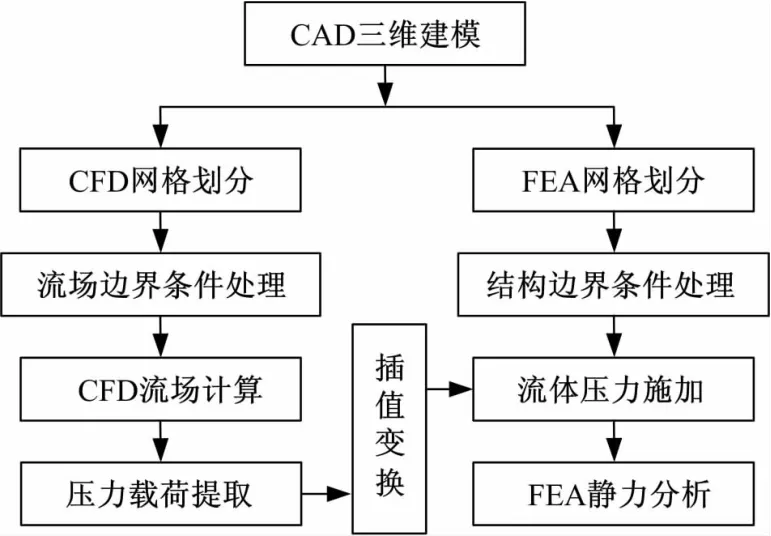
图1 单向FSI分析流程Fig.1 Flow chart of one way FSI analysis
针对本文研究的冲焊型液力变矩器叶轮的焊接强度问题,假设变矩器叶轮及叶片的变形量对流场的影响较小,所以采用单向FSI分析方法。叶轮焊接强度计算是在内部流场计算的基础上进行的。
2 计算模型的建立
2.1 CFD计算模型的建立
本文首先采用CFD软件对某冲焊型液力变矩器内流场进行数值仿真。该变矩器循环圆有效直径为255mm,其中泵轮叶片数为21个,涡轮叶片数为28个,导轮叶片数为17个。图2为工作腔的流道几何模型和网格模型。
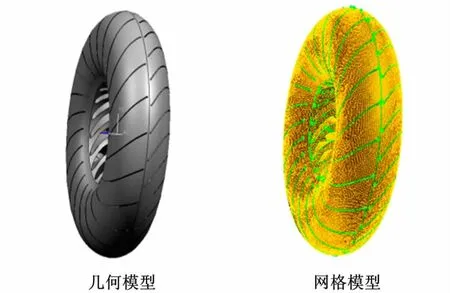
图2 流道几何模型和网格模型Fig.2 Geometric model and grid model of flow channel
计算采用分离式求解器;压力速度耦合算法采用SIMPLE算法;空间离散格式采用二阶迎风格式;边界条件采用壁面边界(Wall)和交互面(Interface)两种;采用滑动网格技术来解决流体计算中两个不同区域的相互交互作用[9]。湍流模型采用大涡模拟(LES)。其基本思想是:用瞬时的Navier-Stocks方程组直接模拟湍流中的大尺度涡,而小尺度涡对大尺度涡运动的影响则通过建立亚格子尺度模型来模拟。通过前期大量计算,发现采用大涡模拟计算出的扭矩与实验值误差较小,并且三个叶轮平衡扭矩最接近0值,说明采用大涡模拟时力的计算结果与实际最为接近。
图3为制动工况下,工作流场中提取出的涡轮叶片工作面和非工作面上的静压力分布图。其上的流场压力通过FSI作用的边界面施加给叶片结构。
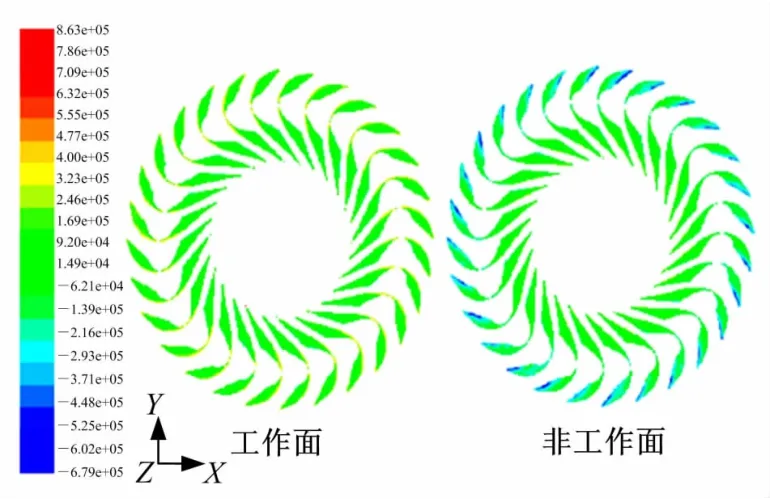
图3 涡轮叶片静压力分布Fig.3 Static pressure distribution of turbine blades
2.2 插值变换
在FSI计算中,由于CFD和FEA计算网格在交换界面上的网格节点不相匹配,需对两个物理场耦合面上非匹配网格进行插值变换。本文利用Matlab中的插值命令TriScatteredInterp来完成网格差值变换。该方法避免了大量繁琐的狄洛尼三角的构建,在不需要重新进行三角化的前提下可以对样本点的数据值进行调整。此种插值算法稳定性好、速度快、精度高,能够得到较好的插值效果。
对液力变矩器的工作流场进行CFD数值计算后,将流场耦合面上的各节点压力值及对应的节点坐标以ASCII文件类型输出。在CFD数值计算中泵轮流道和涡轮流道将沿着Interface面做相对滑移,所以在做流体网格和结构网格的插值映射前,需通过坐标变换,将CFD和FEA模型的耦合边界面相对应。在CFD仿真中提取计算前耦合面上的各节点坐标与计算后相对应的节点压力值用于插值变换。在流固耦合面上,对流体网格和结构网格进行插值映射,可以得到作用在焊接叶轮耦合面上较为准确的流体压力载荷。
2.3 FEA模型的建立
(1)建立网格模型
本文研究的某型冲焊型液力变矩器采用钎焊的焊接方法,焊接工艺和焊接填充金属强度对叶片与内外环连接处的强度有重要影响,而叶片与内外环的滚铆连接会使计算更加复杂,难以保证计算精度,因此本文暂未考虑叶片与内外环的滚铆连接,在有限元前处理软件中对液力变矩器及其焊缝结构进行了简化处理。依据涡轮结构特点,采用自适应网格划分方法划分四面体网格。叶片两侧焊缝与内外环采用共节点处理。建立接触面、目标面、约束面、叶片载荷面的节点组件。涡轮结构网格模型如图4所示,其中四面体单元采用SOLID185单元模拟;所选内外环材料为10F,叶片材料为08Al,焊点材料为H68。材料属性如表1所示。
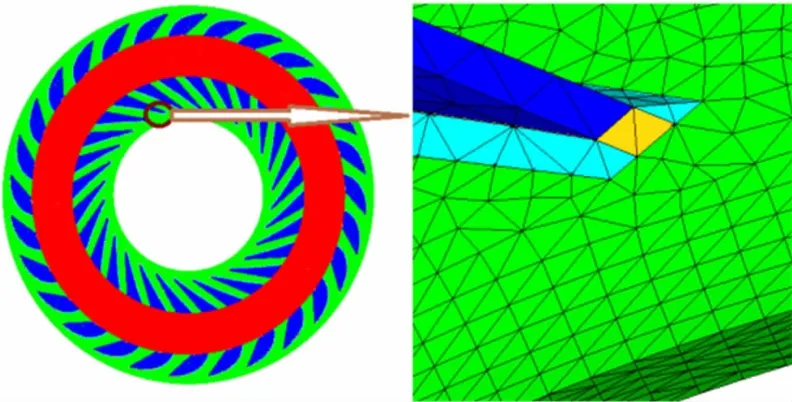
图4 网格模型图Fig.4 Grid model diagram
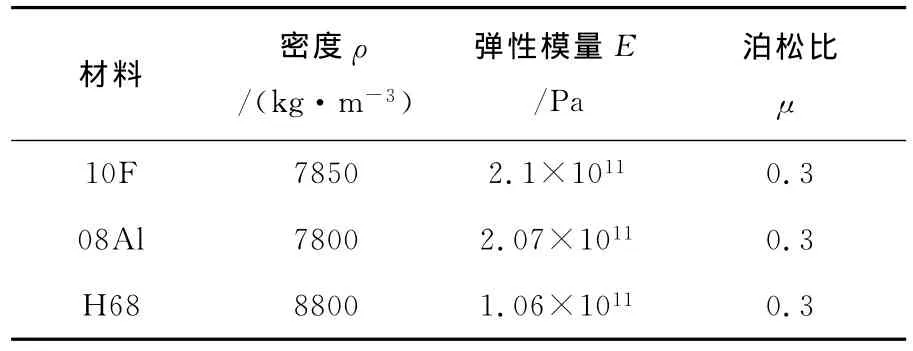
表1 材料属性Table 1 Material properties
(2)定义接触
接触问题是一种高度的非线性问题。接触问题的关键在于接触体之间的相互关系,包括接触前后的法向关系和切向关系。在法向上必须实现接触力的传递和接触面间没有穿透。
本文研究的某型冲焊型液力变矩器,叶片与内外环是通过钎焊衔接为一体的。为真实模拟各部件间的传递力,应用ANSYS软件对叶片和内外环结构进行面-面的非线性接触设置,计算中采用扩展的拉格朗日乘子法,使用Targe170和Conta173来定义3-D接触对。模型中共28个叶片,分别与内外环接触,共计56个接触对,如图5所示。
(3)施加约束
对于变矩器叶轮结构,泵轮与泵轮轴、涡轮与涡轮轴的连接均在叶轮中心的圆柱面上,因此,本文在涡轮轴孔处施加全约束。
(4)施加载荷
液力变矩器叶轮在工作时承受的载荷主要包括两种:①在高速旋转中叶轮自身重量形成的结构惯性离心力;②工作腔内循环流动的工作液体作用在叶轮上的流体压力。本文以典型的涡轮制动工况为例进行分析,转速比i=0,涡轮不承受离心力,仅施加流体压力载荷。
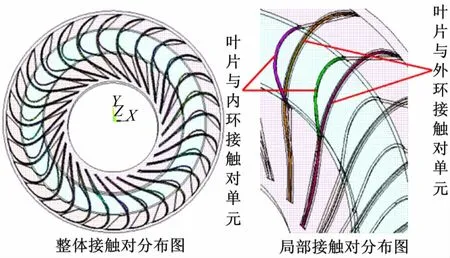
图5 接触对分布图Fig.5 Distribution map of contact pair
3 结果分析
3.1 整体位移和应力云图
如图6所示,叶轮最大变形为0.01057mm,位于叶片进口靠近外环侧及外环靠近进口端。由图7可知,涡轮结构的最大应力为42.4MPa,发生在叶片出口与内环相接的根部。
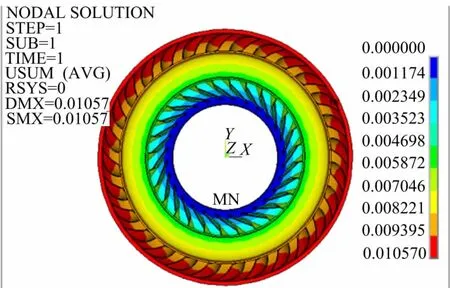
图6 涡轮结构位移云图Fig.6 Deformation contours of turbine structure

图7 涡轮结构应力云图Fig.7 Stress ontours of turbine structure
3.2 焊缝处应力云图
图8为叶片两侧与内环衔接的焊缝结构应力云图,最大应力值为29.2MPa,出现在叶片出口靠近内环的端部,为应力集中。原因是由于模型中该处非圆滑过渡简化造成的。内环焊缝工作面处的整体应力由中间向进出口两侧递增,在出口段应力最大。
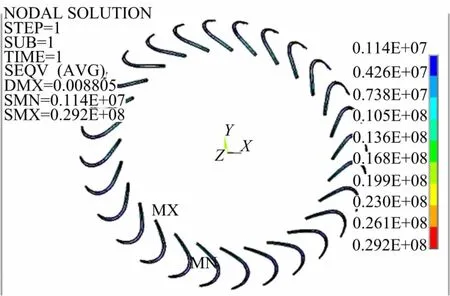
图8 内环焊缝结构应力云图Fig.8 Stress contours of inside ring weld structure
图9为叶片两侧与外环衔接的焊缝结构应力云图,最大应力值为11.4MPa,出现在叶片出口靠近外环的端部附近,应力面积较大,但应力级别小,整体应力分布同内环结构。
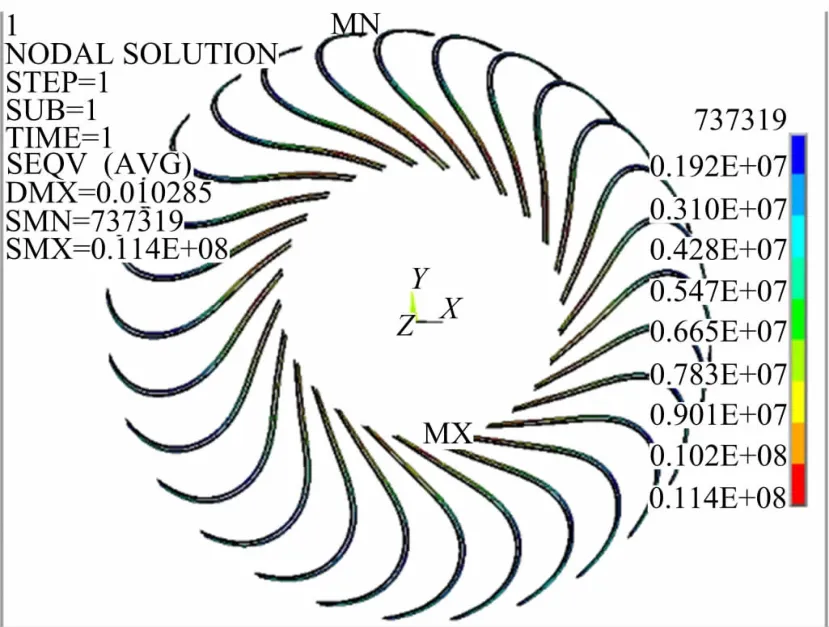
图9 外环焊缝结构应力云图Fig.9 Stress contours of outside ring weld structure
3.3 接触应力云图
图10为叶片与内环接触面的接触应力图,最大接触应力值为58.9MPa,出现在叶片中间位置处,为内环滑动接触;图11为叶片与外环接触面的接触应力图,最大接触应力值为56.4MPa,出现在叶片端部处,为外环滑动接触。由接触应力云图可知,制动工况下涡轮结构面与面的平均接触应力在12MPa左右。
从上述的分析结果可以看出:在流体压力载荷作用下,叶轮的总体变形量较小(最大值为0.01057mm,且结构与流场直接作用区域的变形量更小),不会对流场造成明显扰动,所以本文按照单向FSI理论对某冲焊型液力变矩器叶轮系统的焊接强度进行分析是合理的。
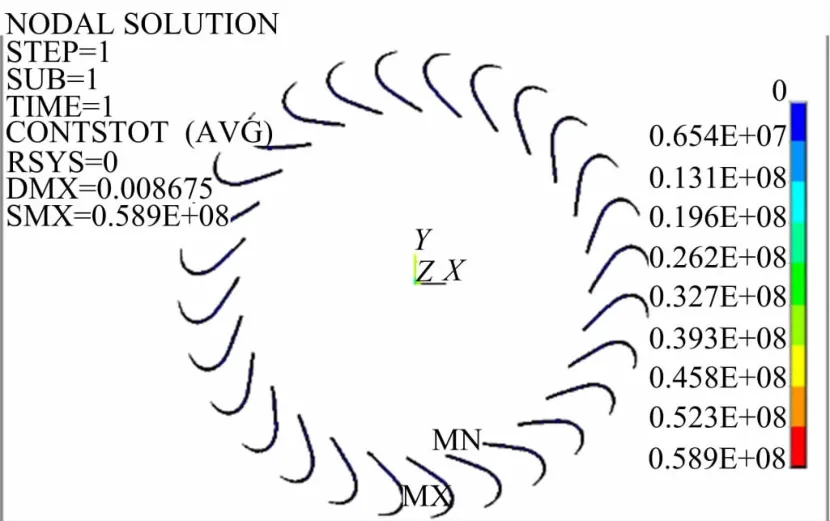
图10 叶片与内环接触应力云图Fig.10 Contact stress contour of blade and inside ring
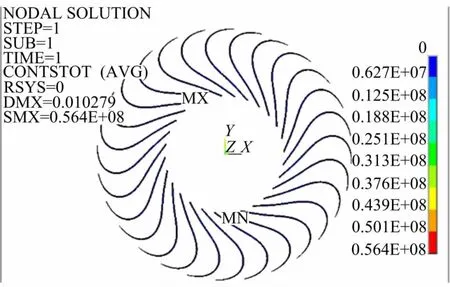
图11 叶片与外环接触应力云图Fig.11 Contact stress contour of blade and outside ring
本文研究的冲焊型液力变矩器内外环材料的屈服极限为232MPa;叶片材料的屈服极限为215MPa;焊点材料的屈服极限为269MPa。而在制动工况下涡轮结构极限应力值为42.4MPa,极限接触应力为58.9MPa,远小于材料的屈服极限值,强度满足要求。
4 结 论
(1)提供了一种对冲焊型变矩器焊接强度的计算方法。对叶片两侧焊缝与内外环采用共节点的方法模拟焊接结构;叶片与内外环部件间采取接触设置,进行接触非线性分析。通过该方法可真实模拟构件传力,更好地掌握结构变形情况和应力分布。
(2)采用单向FSI分析方法对冲焊型液力变矩器叶轮的焊接强度分析是可行的。本文的研究工作对冲焊型液力变矩器的结构设计及分析具有重要的指导意义和参考价值。
[1]Tomasz Kietlinski,Michael Fingerman.248mm elliptical torque converter from daimlerchrysler corpo-ration[C]∥SAE Paper,2007-01-0241.
[2]Kim B S,Ha S B,Lim W S,et al.Performance estimation model of a torque converter partⅠ:correlation between the internal flow field and energy loss coefficient[J].International Journal of Automotive Technology,2008,9(2):141-148.
[3]Toru Ochi,Hiroaki Takeuchi,Hiromichi Kimura,et al.Development of a super-flat torque converter for the new Toyota FWD 6-speed automatic transaxle[C]∥SAE Paper,2006-01-0149.
[4]魏巍,闫清东,朱颜.液力变矩器叶片流固耦合强度分析[J].兵工学报,2008,29(10):1158-1162.Wei Wei,Yan Qing-dong,Zhu Yan.Strength analysis of fluid solid interaction field of hydrodynamic torque converter vanes[J].Acta Armamentarii,2008,29(10):1158-1162.
[5]闫清东,刘树成,姚寿文,等.大功率液力变矩器叶轮强度有限元分析[J].兵工学报,2011,32(2):142-146.Yan Qing-dong,Liu Shu-cheng,Yao Shou-wen,et al.A finite element analysis of blade whell strength of a high-powered torque converter's[J].Acta Armamentarii,2011,32(2):142-146.
[6]陆忠东,吴光强,殷学仙,等.液力变矩器流固耦合研究[J].汽车技术,2009(2):37-41,57.Lu Zhong-dong,Wu Guang-qiang,Yin Xue-xian,et al.Study on fluid-solid interaction of torque converter[J].Automobile Technology,2009(2):37-41,57.
[7]王彬,杨庆山.弱耦合算法的实现及其应用[J].工程力学,2008,25(12):48-52,59.Wang Bin,Yang Qing-shan.The realization and application of loosely coupled algorithm[J].Engineering Mechanics,2008,25(12):48-52,59.
[8]王洋,王洪玉,张翔,等.基于流固耦合理论的离心泵冲压焊接叶轮强度分析[J].农业工程学报,2011,27(3):131-136.Wang Yang,Wang Hong-yu,Zhang Xiang,et al.Strength analysis on stamping and welding impeller in centrifugal pump based on fluid-structure interaction theorem[J].Transactions of the CSAE,2011,27(3):131-136.
[9]刘春宝,马文星,朱喜林.液力变矩器三维瞬态流场计算[J].机械工程学报,2010,46(14):161-166.Liu Chun-bao,Ma Wen-xing,Zhu Xi-lin.3Dtransient calculation of internal flow field for hydrodynamic torque converter[J].Journal of Mechanical Engineering,2010,46(14):161-166.
