班车站点及路线的优化设计

冯存梅 李 威 沈 忱

（1.上海电机学院 电子信息学院，中国 上海201306；2.上海电机学院 机械学院，中国 上海201306）

0 研究背景

班车站点及线路的优化设计是属于典型的车辆路径问题（Vehicle Routing Problem,即VRP 问题）。VRP 问题在国外最早是由Dantzing 和Ramser[1]于1959 年首次提出的。早在1962 年，Balinski 等人就提出集分割[2]，直接考虑可行解集合并在此基础上进行优化建立了最简单的VRP 模型。1971 年，Eilon 等人[3]提出将动态规划法用于固定车辆的VRP,通过递归方法求解。1991 年，Gendreau 等人[4]将禁忌搜索方法应用于VRP。M.L.Fisher 于1995 年 在 “Vehicle Routing Handbooks in Operations Research&Management Science”[5]中对车辆路径问题作了总结，他把车辆路径问题的研究方法归结为三个阶段。第一个阶段，是20 世纪60 年代到70 年代，这个阶段主要是应用一些简单的启发式方法来研究车辆路径问题，研究的重点主要局限于局部搜索和交换技术；第二个阶段，是20 世纪70 年代到80 年代基于启发式方法的设计阶段，这个阶段主要是利用不同于一般启发式方法的近似优化算法来求解车辆路径问题。到了第三阶段，即20 世纪80 年代至今，研究的重点主要放在精确的优化算法和新兴的人工智能算法，包括模拟退火算法、禁忌搜索算法、遗传算法和人工神经元网络方法[6]。

在国内对VRP 研究最早的是郭耀煌教授，1989 年郭教授与其学生就多车场多车型等问题进行了研究[7]。1999 年姜大立等人[8]建立了VRP 的遗传算法。2001 年，李嘉等人[9]设计了遗传算法和禁忌搜索启发式的混合算法。2004 年崔雪丽等人基于人工蚂蚁系统给出了快速求解VRP 的蚂蚁搜索算法。还有不少研究者均对VRP 的研究做出了很大的贡献。单这些研究都是理论的东西，能够更好的解决实际问题才能说明研究的价值。所以这些研究应该更偏向实际问题。

1 符号说明

M 企业或单位乘车总人数

L 总车辆数(k 表示第k 辆车)

Z 总站点数

N 总路径数

C 每辆车的容量

Si第i 条路线

Pi第i 个站点

Yi第Si条路线的总乘客数

ωijk车辆k 从Pi站到Pj站的路程

Tijk车辆k 从Pi站到Pj站经历的时间

2 班车站点设置的数学模型

设置站点的第一步是统计企业或单位的所有乘客的住址坐标（即住址所在的经纬度可利用google earth 标出）。记每位乘客的住址坐标为（ri，ci）（ri为经度ci为纬度）。假设共要设置站点Z 个,第j 个站点的坐标为（xj，yj）（xj为经度yj为纬度）。[10]

为使每位乘客到达站点距离的总路程最短及每位乘客到达站点的距离均衡以下给出总距离函数和最大距离与最小距离之差函数：

在设置站点的过程中还要考虑乘客到达站点所能承受的最大距离。假设乘客所能承受的最大距离为d1则有：

在衡量总距离与最大最小距离偏差时可在两函数前加权重系数以更清楚地反映实际情况，综合以上，可建立如下班车站点设置的数学模型：

3 路线的优化设计

线路的设计优化模型建立过程中我们从多样性角度出发并结合实际情况建立了两种线路的模型。和多数研究者不同我们考虑了实际班车站点和路线在不同企业或单位中有些比较复杂但有些比较简单，复杂的问题往往会有更多的目标和约束条件，解的过程也要复杂很多这是一种情况。在相对简单的情况若仍按照复杂模型的思路和计算方法不仅得不到较好的结果还会浪费过多的时间和精力，是不经济也是不实际的。因此我们建立了根据站点数量不同而路线安排也不同的两种模型。即以下的模型一和模型二。

模型一：

此模型是针对一些乘客人数较少，站点较少或运输资源有限等条件下建立的单一车辆单一路经的数学模型。仅仅适用于小型企业或单位，这种模型相对简单但在实际应用中却是经常要用到的。

在建立此模型中我们假设只有一辆车，车的容量足够容纳所有乘客。在站点已知且站点数目不是很多（说明：站点不多是指在总乘客数小于车容量下站点数一般小于20 个，此处20 只是对一般情况的假定，实际中具体个数应按实际需要设定）的情况下要求：①车要经过所有站点②车的路线最短③车辆行驶时间最短④除特殊情况外每个站点只经过一次（说明：特殊情况是指如不再次经过此站点车辆无法返回）。

从以上要求中可以看出此问题应属于TSP （Travelling Salesman Problem）问题。此问题仍属于NP-Complete 难题，许多学者在此问题上都花费了大量的精力但目前仍没有彻底解决该问题的方法。这并不意味着此处是做无用功，在简化数据和理想化一些条件后仍有一些有效的解决方法。

在上述要求中没有提及成本问题，其实对于单一车辆单一路径，车辆的成本是固定的。剩余的就只有运行的成本，运行的成本只与路程有关即只要求。

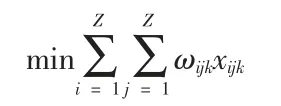
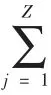
由以上要求可建立模型如下：

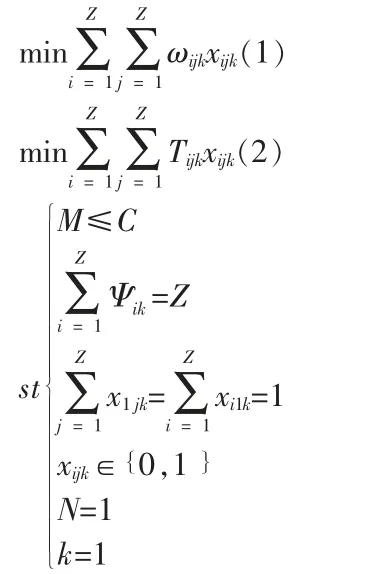
对目标函数（1）（2）其中（1）表示车辆行驶总路程最短（2）表示车辆行驶时间最短。对单一路径来说当车速一定时，路程和时间是成正比的。但为什么此处既对路程进行约束又对时间进行约束在此说明一下。在下文中会涉及道路饱和度的因素当满足（1）时在某些情况下会因为道路达到饱和而使运行时间过长，此时就会受到（2）的约束改变路线即使行驶路程增加但行驶的时间却比原先减少了，这样更有利于车辆运行效率，也更符合实际情况。第一个约束条件表示乘客总数不大于车的容量。第二个约束条件表示车必须经过每一个站点。第三个约束条件表示车从1 站点出发必须回到1 站点（假设1 站点为目的地）。第四个约束条件表示变量x 的0-1 约束。第七第八约束条件分别表示只有一条路径和只有一辆车。

模型二：

此模型较模型一要复杂，是更具有广泛性和实用性的一般性模型。模型二是针对多人员多站点多线路多种因素综合考虑建立的。因为是一般性模型所以模型二较模型一相比具有多条线路，多车辆。在设置好站点后我们先用floyd 算法求出所有站点之间的最短路，由最短路依次从距原点最远，第二远…第N 远为起点设置N 条线路，设置线路按两条原则一是尽量走最短路二是所有线路尽量囊括所有站点对有些特殊情况则另作分析。具体方法见模型算法设计。

在多条路线中车辆数既不能少于总需求量也不能过多，车辆数是决定成本的重要因素所以目标函数首先应满足使总车辆数达到最少。即：

车辆达到最少是首先决定因素其次是使所有车辆行驶总路程最短，因为除车辆的固定成本外路程所决定的运行成本从长期来看也是重要的因素。即：

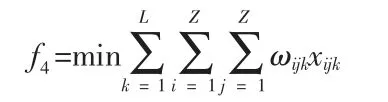
同样在保证总路程最短的前一约束下还要使时间达到最小化。设定时间的约束原因如模型一中设定时间约束的一样，同样是因为道路饱和度的考虑，其约束如下：

在所有路线中为出于对乘客满意度和公平性的考虑应使最长路线与最短路线的差值在一定的可接受范围内，假定最大差值为d2则有：

综合以上模型可建立如下：

min（α2f2＋α3f3＋α4f4＋α5f5）

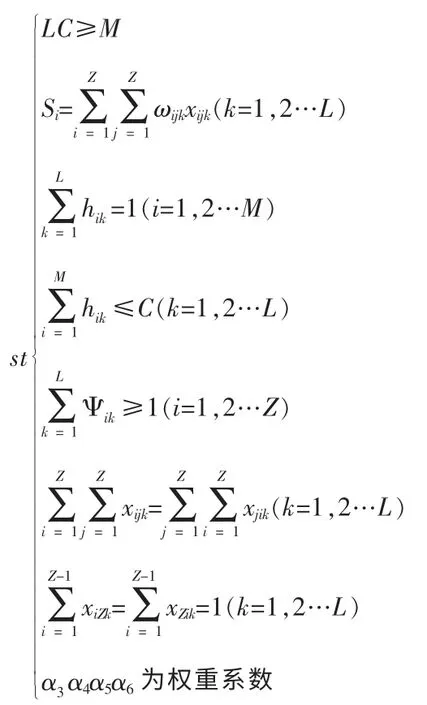
以上模型中目标函数的意义在上文中已说明此处说明一下约束条件的意义：约束条件一表示运载能力的限制即最大运载量要大于总人数。约束条件二表示每条路线的距离。约束条件三表示任意一位乘客只能乘坐一辆车。约束条件四表示每辆车的载客量不超过车的容量。约束条件五表示任意站点至少有一辆车经过。约束条件六表示同一辆车可以从pi站到pj站也可以从pj站到pi站即下行方向为上行方向的反向。约束条件七表示上行方向各路线的目的地为终点站下行方向各路线的发车点为终点站（假设第Z 站为终点站）。

4 道路饱和度的考虑

此处道路饱和度并没有用符号在模型中表示出来是出于对模型求解可行性的考虑，因为就算没有考虑道路饱和度此模型的求解也相当困难。但是道路饱和度是实际问题中不得不考虑的一项因素，特别是在大城市的上下班高峰期，往往会因为交通堵塞浪费大量时间这是很不合理的。此处对道路饱和度的考虑，实际上也是对路线的修正因为在有些已达到饱和的道路再安排车辆通行就不满足时间的约束，就需要对线路进行调整。因为道路什么时候达到饱和往往与时间有关，这就要根据对不同环境的实际经验来判定。当道路达到饱和时即通行时间远超正常通行的时间，就在此时刻对此线路采用绕道而行的调整方案。

例如车辆k 在某时刻t 从pi站到pj站，在时刻t 此时道路ωijk达到饱和。则车辆k 在pi站与pj站途中绕经pα站，若满足Tiαk＋Tαjk＜Tijk原来的路径就改为车辆K 从pi站到pα站再到pj站。这样虽然多走了一些路程但却节省了一部分时间从效率角度讲这样做是合理的。

但对时刻t 模型和算法中是无法给出的，因为其一t 的数值无法确定其二t 具有不稳定性即每天情况可能不一样，只有根据实际经验才能确定。模型算法最终给出的结果只要根据实际经验来作调整即可，所以此处只做说明。

5 站点设置的算法设计

因为对不同的案例站点的设置千变万化，无法给出一个能保证最优最精确的解，所以站点设置算法我们采用一般情况下的启发式算法。如上文所描述模型思想按照算法步骤在一般情况下均可得到较满意的结果。

（1）输入：乘客到达站点所能承受的最大距离d1以及距离函数与距离偏差函数的权重系数α1，α2；

（2）在地图上标注出每一位乘客的住址（ri，ci）（实际操作可用google earth 由经纬度标注出）；

（3）在地图上建立合理的坐标系将乘客住址的经纬度转换成坐标系中的实际坐标；

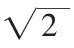
（5）统计出总的区域个数Z 和每个区域的住址点数及乘客数M；

（6）计算出每个圆或矩形的中心（此中心为该区域总路程最短的中心或住址点的重心），并将这些点的坐标作为站点的地理位置；

（7）输出：所有的站点位置的坐标及每个站点的人数。

6 路线模型一的算法设计

对于路线一可看做是简化的TSP 问题,在图论中有类似像哈密尔顿图以及二次逐次修正法这样解决行遍性问题的一般方法。哈密尔顿图的定义：设G＝（V，E）是连通无向图，经过G 的每个顶点正好一次的路径称为G 的一条哈密尔顿路径，经过G 的每个顶点正好一次的圈称为G 的哈密尔顿圈或H 圈，含H 圈的图称为哈密尔顿图或H 图。[11]

在推销员问题中经过每个顶点至少一次权最小的闭通路称为最佳推销员回路。一般来说最佳哈密尔顿圈不一定是最佳推销员回路，最佳推销员回路也不一定是最佳哈密尔顿圈。像模型一这样求单车路程最短不适合用求哈密尔顿图的方法，而二次逐次修正法虽然是近似解法却往往能给出满意的结果。但二次逐次修正法的前提是要求所解图必须是完备图，对于车辆站点路线来说很少有满足此要求的路线图。这里我们对于不满足条件的图用替代的方法构造成完备图。即用最短路代替没有相邻的点之间的路径。具体算法如下：

1）标记所有站点（v1v2…vi…vj…vn）并计算出所有连通站点之间的距离，做出站点路线图的带权邻接矩阵W。

2）由邻接矩阵W 应用Floyd 算法计算出此站点路线图的最短路。

3）任取初始H 圈：C0＝v1v2…vi…vj…vnv1。

4）由于任取的初始H 圈中有些排列相邻的站点之间在实际中并不直接相邻，所以对这些站点之间的权值由（2）中所求最短路代替。

5）对所有i，j，1＜i＋j＜n 若W（vi，vj）＋W（vi＋1vj＋1）＜W（vivi＋1）＋W（vjvj＋1）则在C0中删去边（vivi＋1）和（vjvj＋1）加 入边（vi，vj）和（vi＋1vj＋1），形成新的圈C，即：C＝v1v2…vivjvj－1…vi＋1vj＋1…vnv1。

6）对C 重复步骤⑷直到条件不满足为止，最后求得的C 即为最佳H 圈。

7）将所求H 圈中站点序列从发车站依次记录最终所得站点序列的路径即为模型一的车辆路径。

7 路线模型二的算法设计

模型二是属于多线路的一般性模型，对于此类模型的求解大部分研究者都用了像遗传算法，启发式算法，蚁群算法，动态优化法等算法。本文也不例外采用了启发式算法，因为这个模型本身就比较复杂再由于实际情况的各种变化，很难给出能解出稳定结果的算法。启发式算法虽然不一定能给出准确结果，却能根据实际经验在复杂的环境中给出让人较为满意的结果。其算法过程具有可调节性，在不同条件下很容易根据实际情况调整，使其更切合实际。具体算法如下：

1）输入：最长路线与最短路线的差值的极限值d2，客车容量C，各个站点的坐标位置和各站点人数。

3）由Floyd 算法根据个站点路线图计算出最短路。

4）在最短路中取距终点最远的L 个站点，根据距终点的距离由大到小分别计为线路S1S2…SL的起始站点。

5）从S1开始按最短路到终点确定第一条路线，依次确定L 条路线。

6）调整从S2到SL的L－1 条路线，调整的原则为：①将未在路线中的站点调整至路线中；②站点调整时只将此站点纳入据此站点最近的路线中；③调整过程中路线以走最短路为优先原则。若所有未在路线上的站点均调整在了路线中则转（7）。

7）在所有站点均考虑的前提下，计算出每条路线的路程分别计为S1到SL的实际值，若max（Si－Sj）＞d2则转至（6）重新调整路线直至max（Si－Sj）≤d2则转至（8）。

8）计算每条路线上总乘客数，有多条路线经过同一站点时只将此站点计算至其中一条路线。若Yi＞C 则将Si中Yi－C 个乘客交换到其他路线（以有重合站点的一对路线为优先原则进行交换）。直至对所有路线均有Yi≤C。

9）输出：S1至SL中L 条路线的站点路线以及每条路线所包含的站点，每个站点的上车人数在不同路线的分配。

［1］Dantzig, Ramser. The truck dispatching Problem, MgtSci[M]. 1959, 6: 81-85.

［2］Balinski M, Quand R. On an integer program for a delivery problem [J].Operations Research, 1962,12: 300-304.

［3］Eilon S, Watson -Gandy C DT, Christofides N. distribution management:mathematical modeling and practical analysis [M].London: Griffin, 1971.

［4］Gendreau M, Hertz A, LaporteG A. tabu search heuristic for the vehicle routingproblem[M]. Montreal: Publication#777, Centre de recherchesur lestranspors,1991.

［5］M.L.Fisher.Vehicle Routing Handbooks in Operations Research & Management Science. Vol8, 1995[S].

［6］金燕波.校车路径优化问题研究[D].吉林大学,2006.

［7］郭耀煌.安排城市卡车行车路线的一种新算法[J].统工程学报,1989,4(2)70-78.

［8］姜大立,等.车辆路径问题的遗传算法研究[J].系统工程理论与实践,1999(6):40-45.

［9］李嘉,等.一类特殊车辆路径问题(VRP)[J].东北大学学报:自然科学版,2001,22(3):245-248.

［10］张富朱泰英.校车站点及线路的优化设计[J].数学的实践与认识,2012-02-23.

［11］Herbert Fleischner.欧拉图与相关专题[M].科学出版社,2012-04.