概率密度估计中的核非方法及应用研究

文仕军

(贵州大学 计算机科学与技术学院，贵州 贵阳550025)

0 引言

以统计数据分析为主要目的学习问题被分为三个基本问题：模式识别、回归估计和概率密度估计。在解决学习问题的传统理论中，模式识别和回归估计都是建立在概率密度估计的基础上的。概率密度估计通常采用参数估计和非参数估计的方法[1]。参数方法是根据经验，假定总体的分布为某种特定的形式，如高斯分布、瑞利分布等，而未知总体分布的某些具体参数值，然后再用样本计算出这些未知的参数值。但在实际应用中，样本数据总是有限的，有时并不能确定总体的具体分布。当对总体的分布形式无法做出大致正确的判断时，需要采用一种非参数方法更为合理，直接从样本入手进行估计，即非参数估计方法。非参数统计方法几乎不对总体设立限制条件，非参数估计可以处理所有类型的数据[2]。

概率密度估计是统计学中的一个核心问题，得到概率密度，就可以解决概率有关的问题。因此，求解概率密度问题在理论研究和实际问题中都有重要的意义。在非参数密度估计中，常用的方法有Parzen窗法和SVM 等。Parzen 窗估计需要尽可能多的估计样本，窗宽的取值也影响估计的精度；SVM 估计需要采用非线性规划的手段实现，虽然在样本有限的情况下也能达到一定的精度，但是算法复杂，样本规模较大时训练速度较慢。本文介绍一种简单有效的估计方法，称为核非线性回归（KNR，Kernel-based Nonlinear Regression）法。

1 密度估计的经典方法

1.1 概率分布及概率密度

对于随机变量X 的分布函数F(x)，存在非负函数f(x)，使对于任意实数x 有：

则称X 为连续型随即变量，其中函数f(x)称为X 的概率密度函数。

1.2 概率密度估计的经典方法

1.2.1 极大似然估计

对于独立同分布的样本数据x1，x2，…，xN，定义似然函数为：

其中，密度是θ 的函数。

将似然函数（2）表示成对数形式：

则最大似然函数的估计量即为式(3)表示的微分方程的解[2]。

1.2.2 经验方法：统计直方图[3]

设X1，X2，…，Xn是取自总体X 的样本，x1，x2，…，xn表示样本观测值，令：

其中i=1，2，…，n，j=1，2，…，k，则得到：

式（7）为采用经验方法估计得到的密度函数。

2 密度估计的核非法

2.1 Parzen 窗法

定义以原点为中心，半径为1/2 的邻域函数为：

式（9）为Parzen 窗密度估计，其中h 为窗宽[3]。

2.2 基于SVM 的密度估计

用SVM 方法来估计概率密度，就是从概率密度的定义出发，直接求解该线性算子方程。它结合了不适定问题的理论、传统的非参数统计学以及统计学习理论等方面的思想。支持向量机是通过事先选择好的某一个非线性变换，将输入向量x 映射到高维空间Z，在这一特征空间中，构造一个最优超平面[4,5]。

利用SVM 求解概率密度估计问题，主要是首先在像空间中定义相应的回归问题，然后利用支持向量机法构造求解回归问题的核函数K(xi，xj)和交叉函数κ(xi，t)，最后根据核函数，利用支持向量机方法求解回归问题，找出支持向量和对应的系数，具体过程为：

使用SVM 方法解线性算子方程：

方程（10）的解可以表示成如下形式：

将式（11）表示成函数集的形式：

在式（12）最小化泛函，即寻找目标函数。通过算子A，该函数集映射为：

定义像空间中的核函数为：

利用SVM 方法解线性算子方程就可以表达为利用核函数和数据对(x1，Fl(x1))，…，(xl，Fl(xl))在像空间中进行回归估计，获得w，并通过交叉核函数得到线性算子方程的解：

其中，κ(xi，x)为核交叉函数，式（16）是对未知的概率密度f(x)进行回归估计得到的结果[4-5]。

2.3 基于KNR 的密度估计[6-9]

KNR 是一种非线性核回归算法，在图像处理、模式识别中有广泛的应用。再生核k 定义为：设H 是Hilbert 函数空间，其元素是某个抽象集合B 上的实值或复值函数，设k(t，s)是B×B 上的二元函数，对于任何的s∈B，k 作为t 的函数是s 的元素，而且对于任何s∈B 及fk∈H有：

则称设k(t,s)为Hilbert 函数空间的再生核。定义再生核函数为：

则密度函数f(x)为多个核函数叠加而成，表示如下：

其中N 表示样本个数，x 表示样本元素，a 为系数向量，由最小二乘准则估计出向量a 如下式：

符号“+”表示矩阵的Moore-Penrose 广义逆，并且K 中的第p 行q列的元素为：

其中，x 表示训练向量。

式（20）中，y 表示为：

3 实验结果分析

首先给定高斯分布中的参数值，用高斯分布密度产生100 个随机数，由分布密度（23）产生100 个随机样本，采用正态分布，用极大似然函数法求参数μ 和σ。

其中σ=0.5，μ=3。

用参数法估计的μ=3.0615，σ=0.5812，但这是在已知数据分布的基础上，对已知分布的部分未知参数采用极大似然法进行估计。然后用Parzen 估计、SVM、及KNR 方法法得到估计曲线，与理论曲线进行了对比。由图1 可知，经验密度估计过程中，不需要先验知识，将样本数据的取值范围分成若干个区间，然后把落在每个区间内的数据数目用直方图表示出来，但是估计概率密度精度不高。图2 采用Parzen 核密度估计的方法，根据样本数据得到了概率密度曲线，在核密度估计过程中，窗宽h 的取值会影响估计曲线的光滑程度，h 较大，将有较多的样本点对x 处的密度估计产生影响，Parzen 核密度估计为了提高估计精度，需要尽可能多的样本。由图3 支持向量机概率密度估计曲线可知，支持向量机估计时对样本数据依赖较小，需要少数的支持向量即可，图3 中* 号表示支持向量，估计精度较高时需要的支持向量也较多，支持向量较少的部分估计误差很大，同时由于算法涉及大量矩阵运算，样本训练时间长。由图4 可知，采用KNR 方法后，能够提高估计精度，算法简单，提高了执行速度。

图1 经验密度估计曲线（直方图）

图2 parzen 核估计概率密度曲线

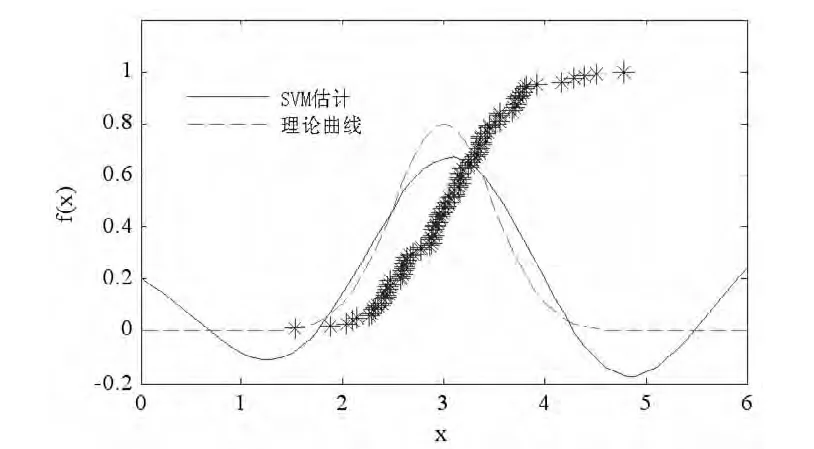
图3 支持向量机估计概率密度曲线

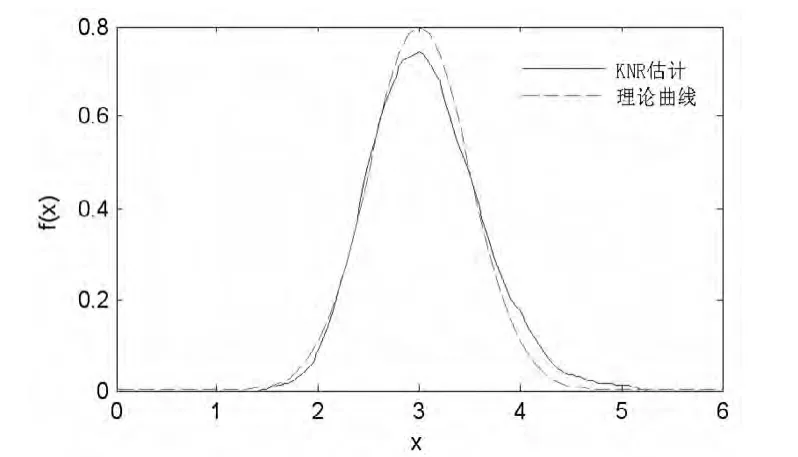
图4 核非法概率密度曲线

4 结论

在对极大似然法、Parzen 等传统的方法进行研究的基础上，采用了一种KNR 的密度估计方法。得到了相关方法估计结果和理论估计结果的对比曲线，由结果可看出，与参数法求解概率密度相比，非参数法可以处理任意形式的概率密度，不存在模型失配问题，但是为了得到精确的概率密度，需要得到大量的训练样本；KNR 方法能够在有限样本的情况下得到较为精确的密度估计。

［1］Vladimir N. Vapnik 著.统计学习理论的本质[M].张学工，译.北京：清华大学出版社，2000.

［2］边肇祺，张学工.模式识别[M].北京：清华大学出版社，2000.

［3］周品.MATLAB 概率与数理统计[M].北京：清华大学出版社，2012.

［4］Weston Jason, Gammerman Alex, Stitson Mark, et al. Advances in Kernel Methods： Support Vector Learning[M]. Cambridge, MA： MIT Press,1999.

［5］张炤，张素，章琛曦，等.基于支持向量机的概率密度估计方法[J].系统仿真学报，2005，17(10)：2355-2357.

［6］Jing Zhang, Benyong Liu, and Hao Tan, A kernel-based nonlinear representor for eigenface classification[J]. JESTC，2004，2(2)：19-22.

［7］Benyong Liu and Jing Zhang. Eigenspectra versus eigenfaces： Classification with a kernel-based nonlinear representor[J]. LNCS, 3610,2005：660-663.

［8］胡业刚，刘本永.小图像放大：算法与评价[J].贵州大学学报：自然科学版，2010，27(2)：78-82.

［9］刘本永.斜投影核鉴别器的增量学习：理论及算法[OL].[2012-10-29],中国科技论文在线,http：//www.paper.edu.cn/ releasepaper/content/201210-288.