一种H桥级联型多电平逆变器SVPWM通用算法实现

朱玉琼，朱方田，方蒽，伍小杰

（中国矿业大学 信息与电气工程学院，江苏 徐州 221008）

1 引言

近年来，多电平逆变器以高耐压和优良的谐波特性广泛应用于大功率场合。SVPWM因其在优化开关顺序和数字实现方面的优势，广泛应用于两电平和3电平控制。对于n电平逆变器，含有3n(n-1)+1个电压空间矢量和n3种不同的开关状态。当电平数多于3电平时，由于含有较多的冗余矢量和开关状态，SVPWM控制策略实现起来相对复杂。对于二极管钳位型逆变器，冗余矢量用来平衡直流侧的电容电压，而对于H桥级联型逆变器，电容均压问题简单，重点考虑减小输出电压谐波和降低器件平均开关频率。

对于多电平逆变器，论文大多采用载波相移调 制 SPWM(CPS-SPWM)技 术［1－2］， 可 实 现 较高的等效开关频率，且调制策略简单，在高压、大功率场合有很好的应用前景。而SVPWM相对于SPWM，直流电压利用率提高15%，且易于数字实现，并可以优化器件开关顺序。文献［3］针对3电平逆变器提出了简化SVPWM算法，将3电平转化为两电平的计算，简化了运算，但应用于多电平时，算法仍然很复杂。

本文实现了一种简单通用的SVPWM算法，并成功应用在3电平H桥级联型逆变器中。理论分析表明，这种方法开关频率较低，仿真结果表明，这种方法输出的电压电流谐波含量小，仿真和实验结果验证了算法的有效性。

2 参考矢量位置的确定和基本矢量作用时间的计算

图1为3电平H桥级联模块，采用独立的直流电源给H桥供电。图2为3电平、5电平、7电平在第1扇区的空间矢量图。例如对于5电平逆变器，共有61个冗余矢量，125种开关状态。

图1 3电平H桥级联模块Fig.1 Three level H bridge cascaded module

图2 3，5，7电平在第1扇区的空间矢量图Fig.2 The space vector diagram of three，five and seven level in the first sector

随着电平数的增加，传统的两电平和3电平的SVPWM算法很难在多电平调制中推广实现。 本文基于 g-h坐标系［4－5］， 实现多电平SVPWM调制，具体步骤如下。

1）坐标变换。将电压参考矢量Vref从 坐标系转化为 g-h 坐标［vrg，vrh］T，再按照小矢量的长度将变换后的矢量归一化，将基本矢量变换到g-h坐标系中。

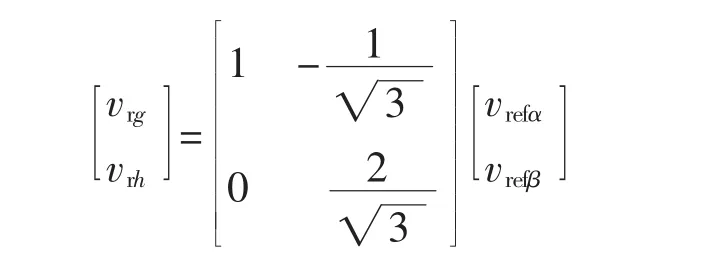
2）确定距离参考矢量最近的3个矢量。为快速确定参考矢量的位置，对参考矢量向上和向下取整，得到4个电压矢量。如图2所示，4个电压矢量分别为

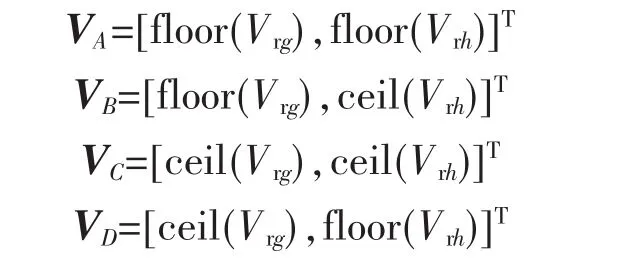
式中：ceil()和floor()函数分别表述对变量向上和向下取整。

再对参考矢量进行逻辑判断，得到最近的3个矢量，即为合成目标矢量的空间矢量：

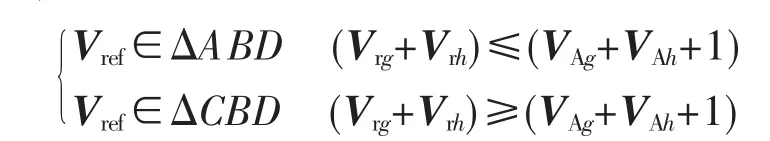
式中：Vxg和Vxh分别表示矢量在g-h坐标系下的坐标。

3）计算矢量的作用时间。在确定了3个基本矢量后，根据伏秒原理求出各个矢量的作用时间。

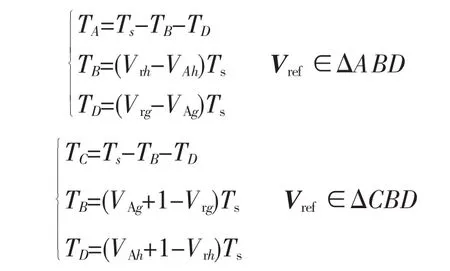
式中：TA，TB，TC，TD是矢量 VA，VB，VC，VD对应的执行时间；Ts为PWM周期。

由矢量作用时间的计算可以看出，容易确定参考矢量的位置和作用时间，且这是一种对任意电平逆变器都通用的算法。

3 基本矢量对应的开关状态

可由通用表达式计算出基本矢量对应的开关状态，设基本矢量V=(Vg，Vh)T，对应的开关状态S=（Sa，Sb，Sc）T。 设电平数为 n，定义 m=(n-1)/2，则

表1 5电平逆变器的开关状态表Tab.1 The switch status of five level inverter

表1为5电平对应的开关状态表。对于5电平而言，开关状态 Sa，Sb，Sc的值均只可以取-2～2之间的整数，因此，随差（Vg+Vh）值的增大，开关状态组合（Sa，Sb，Sc）的种类越少。 如果矢量（1，1）对应的开关状态为（0，-1，-2）、（1，0，-1）和（2，1，0） 3 种，而矢量（2，2）对应的开关状态仅为（2，0，-2）一种。

4 开关状态的选择

在多电平逆变器中，一个空间矢量对应的开关状态可能不止一种。随着电压电平数的增加，同一点对应的冗余矢量增加，这就给多电平开关状态的选择带来困难。如图2所示，若主电路为7电平拓扑，则对于A点，共对应(3,0,1)，(2,-1,0),(1,0,-1),(0,-1,-2),(-1,-2,-3)这 5种开关状态，它们输出的电压幅值和相位均一致。若主电路为5电平拓扑，则A点对应的开关状态只有(2,-1,0),(1,0,-1),(0,-1,-2)3种。

在一个PWM周期中，参考矢量越靠近原点，有越多可供选择的开关状态。若选择的开关状态为3～4种，则时间次序图为1～2电平；若开关状态为5～7种，则时间次序图为2～3电平；若开关状态为 8～10种，则时间顺序为 3～4电平等［6］。如图2所示，若参考矢量位于T1中，即参考矢量在矢量(1,1),(2,1),(1,2)围成的三角形中。若主电路为5电平拓扑，在一个PWM周期中，共含有7种开关状态，三相时间次序图均为3电平，如图3所示。因而在多电平SVPWM调制中，如果使用所有的开关状态，则需要多组调制波与载波比较完成，算法复杂。

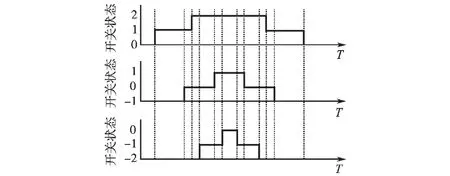
图3 采用全部矢量的调制Fig.3 Modulation by using all vectors

本文针对级联型H桥拓扑，中点电位的问题简单，主要需要降低开关频率，减少系统谐波。为简化算法，将时间顺序简化为两电平，本文采用一组调制波和载波相比较的算法。在选择作用矢量时，只选择中间状态［7］，如A点的中间状态矢量为(1，0，-1)，因而，此方法对任意电平通用。

1）确定中间矢量。本文在开关状态的选择和作用顺序方面进行改进，首先选择中间矢量状态。 设基本矢量 V=（Vg，Vh）T，对应的开关状态 S=(Sa，Sb，Sc)T。当 Vg+Vh为偶数时，中间状态为SM。当Vg+Vh为奇数时，中间状态有2种，分别为小矢量状态Ss和大矢量状态SL。

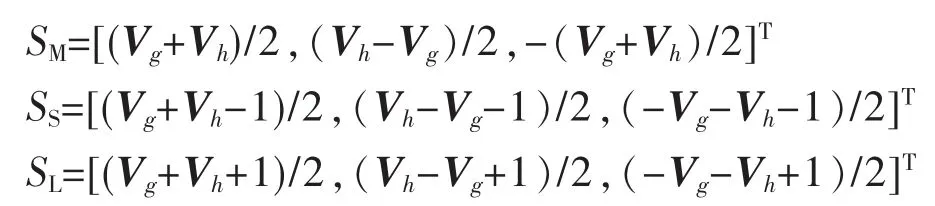
2）等效开关状态。为将时间顺序图简化为两电平，本文采用了等效输出电压的方法，若3个矢量 VA，VB，VC对应的作用时间为 TA，TB，TC。则三相等效输出电压为

其中，当Vg+Vh为偶数时，中间矢量Vmean的作用仅为状态SM作用，当Vg+Vh为奇数时，中间矢量Vmean的作用为状态SS和SL综合作用的结果。

3）开关状态的选择和作用顺序。进行基于三相等效输出电压的7段式开关状态分配。仍以图2中T1为例来说明，图4为两种方法的矢量作用规律调制图，图4a为采用中间矢量，按照矢量作用规律作用的固定调制法调制图。在每个矢量空间的区域范围内，选择的开关状态固定。图4b为等效矢量调制图，即由中间矢量求出三相等效输出电压，再进行开关状态的分配。因此，在每个矢量空间的区域范围内，开关的作用顺序不是固定不变的，而是在每个周期中等效合成的开关状态。

图4 矢量作用规律的调制图Fig.4 The modulation of vector rules

图4a和图4b比较可知，两种策略输出电压等效。且采用等效矢量调制，可以合理地分配开关次序，进而降低器件的开关频率。

图4中，器件平均开关频率［8］fdev分别为

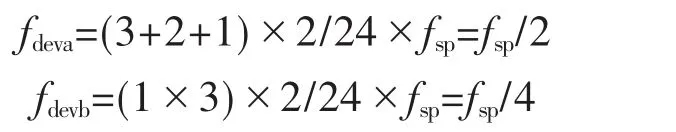
式中：fsp为载波频率。

可见，当矢量位于T1中时，在一个PWM周期中，相对于基于平均矢量的固定调制方法，采用等效矢量调制法，可使器件开关频率减小一倍。

5 仿真和实验结果

5.1 仿真结果

本文采用PLECS仿真软件，以3电平H桥为主电路拓扑进行仿真，采用阻感负载，定义调制比M=Vref/(2Vdc/3)，其中Vdc为逆变器直流母线电压，Vref为电压参考矢量。仿真参数：直流电源电压Vdc=500 V，C1=C2=4700μF，阻感负载电阻10Ω，电感0.01 H，正弦调制波频率为50 Hz，载波频率为 2 kHz。

图5a和图5b分别为当调制比M=0.9时，对应的线电压和电压谐波图。如图5a所示，将开关状态等效SVPWM控制策略运用在5电平逆变器中，输出线电压为9电平。如图5b所示，在0～4 kHz范围内，线电压谐波主要集中在2 kHz左右，且线电压谐波最大值约为基波的6%。

图5 M=0.9时，线电压和电压谐波Fig.5 Line voltage and voltage harmonic waveform when M=0.9

图6a和图6b为当调制比M=0.9时，对应的电流和电流谐波。如图6a可知，电流动态响应快，波形稳定。如图6b可知，电流在2 kHz处谐波最大，且最大值低于基波的千分之五，谐波特性优良。

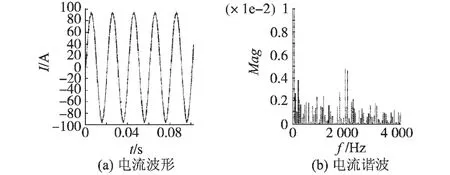
图6 M=0.9时，电流和电流谐波Fig.6 Current and current harmonic waveform when M=0.9

5.2 实验结果

为了验证控制算法，本文实验采用DSP(TMS320F28335)和FPGA来控制3电平H桥级联型逆变器。采用阻感负载 （L=4 mH，R=10 Ω），前级采用二极管整流得二极管两端电压均为 200 V，电容为 4700μF。

当调制比为0.9时，输出相电压和线电压分别为图7和图8所示。对比图5a可知，实验结果与仿真结果相一致，谐波含量较少，实验正确。图9为直流母线电压、线电压和电流的波形，如图9可以看出，直流母线电压稳定，电流波形平稳，谐波小，与仿真结果相符。图10为电压频率改变时的直流母线电压、线电压和电流波形，系统仍有较好的输出特性。

图7 A相电压U a波形Fig.7 A phase voltage U a waveform

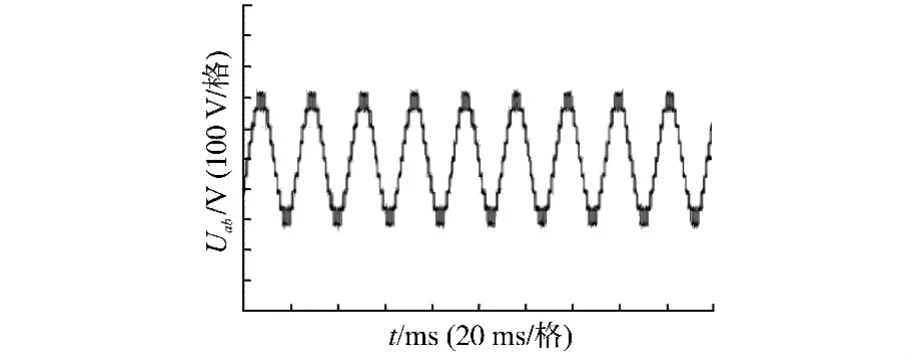
图8 电压U ab波形Fig.8 Voltage U ab waveform

图9 直流母线电压、线电压U ab、线电流Fig.9 DC bus voltage,line voltage U ab and line current waveforms

图10 电压频率改变的波形Fig.10 Waveforms by changing voltage frequency

6 结论

对于H桥级联型多电平逆变器，本文采用简单通用的SVPWM调制，此算法基于g-h坐标系，大大减小了计算量，且计算量与电平数无关。在开关顺序的选择和作用上，采用等效矢量作用法，先选取中间矢量，对这些矢量进行输出电压等效，以等效之后的电压来分配开关顺序，这种方法不仅可以降低器件的开关频率和电压电流谐波，而且适用于任意单元级联型逆变器，具有很好的通用性和扩展性。本文将这种控制策略应用在3电平H桥级联型5电平拓扑中，仿真结果证明了理论分析的可行性，实验结果与仿真结果相一致。矢量的选择对中点电位的影响将是下一步的研究方向。

［1］张颖，李崇坚，朱春毅，等.三电平 H桥级联型逆变器［J］.电工技术学报，2011，18（5）：78－82.

［2］洪春梅.级联 H桥五电平变换器系统研究［J］.电气自动化，2011,33（1）：29－34.

［3］Gupta A K,Khambadkone A M.A Space Vector PWM Scheme for Mu ltilevel Inverters Based on Two-level Space Vector PWM［J］.IEEE Trans.Ind.Electron，2006,53（5）:1631－1639.

［4］Celanovic N，Boroyevich D.A Fast Space-vector Modulation Algorithm for Multilevel Three Phase Converters［J］.IEEE Trans.Ind.Applicat，2001,37（2）：637－641.

［5］WeiS，Wu B，Wang Q.An Improved Space Vector PWM Control Algorithm for Multilevel Inverters［C］∥ Proc.Int.Power Electron，Motion ControlConf.，2004，8（3）：1124 －1129.

［6］Yao W，Hu H，Lu Z.Comparisons of Space-Vector Modulation and Carrier-based Modulation of Multilevel Inverter［J］.IEEE Trans.Power Electron，2008，23（1）：45－51.

［7］McGrath B P,Holmes D G,Lipo T.Optimized Space Vector Switching Sequences for Multilevel Inverters［J］.IEEE Trans.Power Electron.，2003，18（6）：1293－1301.

［8］Cheng Zhongyuan,Wu Bin.A Novel Switching Sequence Design for Five-level NPC／H-bridge Inverters with Improved Output Voltage Spectrum and Minimized Device Switching Frequency［J］.IEEE Trans.Power Electron.，2007,22（6）：2138－2145.