迭代容积卡尔曼粒子滤波算法

王华剑 景占荣 郑文泉 屈保平

(西北工业大学电子信息学院，西安 710072)

近年来，在自动控制、目标跟踪、人工智能、故障检测、数字通信和金融统计等复杂系统中广泛存在着非线性/非高斯的状态估计问题.基于序贯Monte Carlo的粒子滤波(particle filter，PF)利用数值逼近的方式较好地解决了非线性/非高斯系统的参数估计和状态滤波问题.粒子滤波的基本思想是采用随机Monte Carlo对先验分布在状态空间产生一组随机样本集，构建重要性密度函数，递推地用这些随机样本集和其权重来近似于状态变量真实的后验概率密度函数，用样本均值来代替积分运算，从而获得状态的最小方差估计过程［1-2］.

但是由于标准粒子滤波算法选择先验概率密度作为重要性密度函数，没有考虑当前的量测值，从重要性密度函数中取样得到的样本与从真实后验概率密度采样得到的样本有很大偏差，尤其当似然函数位于系统状态转移概率密度的尾部或似然函数呈尖峰状态时，粒子滤波器可能失败［2-3］.为此，国内外学者对如何选取重要性密度函数做了大量的研究.文献［4-7］分别提出了用扩展卡尔曼算法(EKF)、迭代扩展卡尔曼算法(IEKF)、无迹卡尔曼算法(UKF)和迭代无迹卡尔曼算法(IUKF)构建粒子算法的重要性密度函数，虽然均考虑了当前的观测信息，提高了滤波精度，并且IEKF和IUKF算法基于高斯-牛顿迭代思想，利用观测更新得到的状态量对非线性量测方程重新进行线性化，从而减小线性化误差，使得产生的重要性密度函数更加符合状态变量的实际后验概率分布，但是扩展卡尔曼粒子滤波(算法PF-EKF)和迭代扩展卡尔曼粒子滤波算法(PF-IEKF)需要计算雅克比矩阵，这不可避免会引入截断误差，使得状态估计性能提高不大［4-5］，另外无迹卡尔曼粒子滤波算法(PF-UKF)和迭代无迹卡尔曼粒子滤波算法(PF-IUKF)只有在Sigma点集设计合理时，才能得到较好的滤波精度，而在状态高维时若参数选择不当将会引起自协方差非正定，导致滤波性能会降低甚至发散［8-11］.最近，提出了一种基于容积卡尔曼(CKF)［12-13］的粒子滤波算法——容积卡尔曼粒子滤波算法(CPF).该算法使用容积数值积分原则计算非线性随机变量的均值和协方差，避免了求导运算，产生了粒子滤波算法的重要性密度函数，融入了当前的量测信息，使得重要性密度函数更加逼近后验概率函数，其滤波性能得到较好改善，并且实时性较强［14-15］.

本文在CPF的基础上提出一种基于Gauss-Newton迭代思想的粒子滤波算法.该算法利用当前量测信息，通过Gauss-Newton迭代方法对CKF算法进行改进，减小线性化误差，以此来产生粒子滤波算法的重要性密度函数，使得迭代CKF产生的重要性密度函数更接近于真实后验概率分布.仿真结果表明，迭代CKF粒子滤波具有更高的估计精度.

1 容积卡尔曼粒子滤波

容积卡尔曼滤波算法(CKF)采用基于容积原则以数值方式来解决高斯域贝叶斯滤波的积分问

式中，xk，yk分别为系统的状态向量和量测向量;F(·)，H(·)分别为系统状态转移函数和系统量测函数;wk，vk分别为相互独立的过程噪声和量测噪声.

容积粒子滤波算法的基本步骤可参考文献［14-15］.题.它同UKF一样，是一种确定性采样高斯滤波方法，但是CKF相对UKF计算量小，能得到更加精确的滤波效果和稳定性能，且更容易实现［11］.

容积卡尔曼粒子滤波算法是将CKF应用于粒子滤波框架中，使用CKF来产生重要性密度函数，由于融入了当前的量测信息，使得从重要性密度函数中取样得到的样本更加逼近真实后验概率密度采样得到的样本，提高了估计滤波的精度.

考虑如下的离散非线性系统

2 迭代容积卡尔曼粒子滤波

CPF的核心思想是利用CKF产生重要性密度函数，即基于容积原则通过以一组确定的点集和相应的权值来近似得到非线性函数的均值和协方差，以产生CPF的重要性密度函数，但由于量测方程一般为非线性的系统，基于此的做法可能造成量测值得不到正确的利用，从而引入误差.基于Gauss-Newton的量测迭代算法可较好地改善这一问题.

Gauss-Newton迭代算法主要应用于求解非线性最小二乘问题，同时由于CKF是一种非线性次优高斯滤波器，即各个随机量符合高斯分布，则状态量测的最大后验概率更新密度可表达为

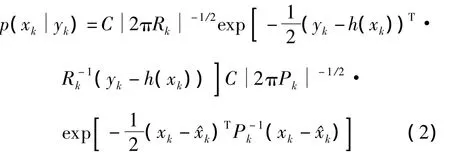
求解上式的最大似然估计即是利用Gauss-Newton对下式“费用函数”的进行最小化求解:

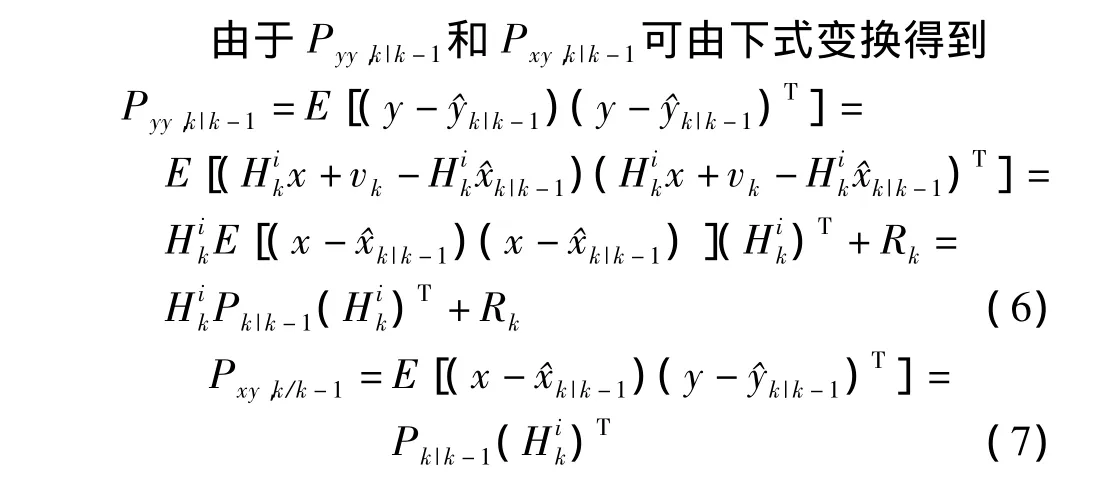
结合Gauss-Newton迭代算法，可得到迭代迭代容积卡尔曼粒子滤波算法的基本形式，其具体步骤如下:

步骤1 初始化.从p(x0)中采样粒子{=1，2，…，N}.

步骤2 每一时刻用迭代CKF算法更新采样粒子，n=1，2，…，N，i=1，2，…，NIter.

步骤3 产生重要性密度函数

步骤4 计算归一化权重

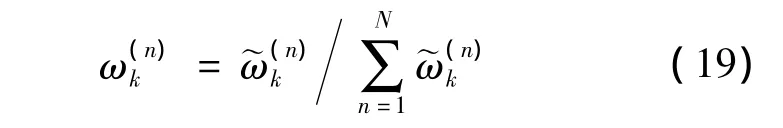
步骤6 输出k时刻的状态和方差估值

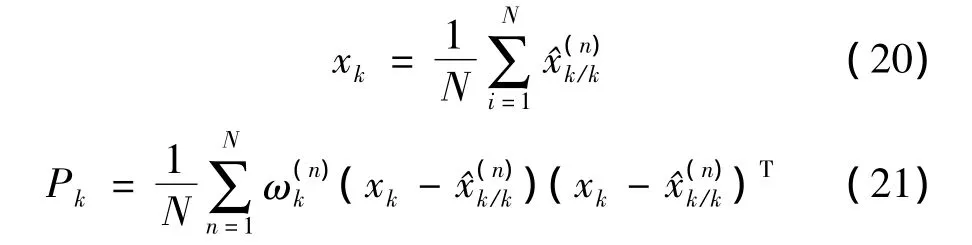
3 仿真结果及分析

对迭代容积卡尔曼粒子滤波在非线性非高斯系统中进行仿真验证，并与PF算法和CPF算法进行分析比较.设系统模型的状态方程和观测方程:

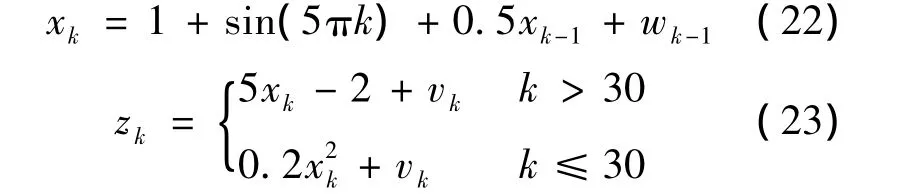
式中，过程噪声服从Gamma分布，wk～Gamma(3，2)，观测噪声服从正态分布vk～ N(0，0.0001)，初始状态x0=1，粒子数N=200，重采样部分采用残差采样法，仿真时间T=60.定义状态的均方根误差为

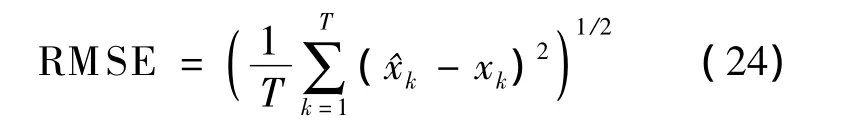
图1给出了PF，CPF和迭代容积卡尔曼粒子滤波器的状态估计曲线，图2为3种算法的均方根估计误差，表1为这3种算法的均方根误差均值和方差及平均运行时间对比.

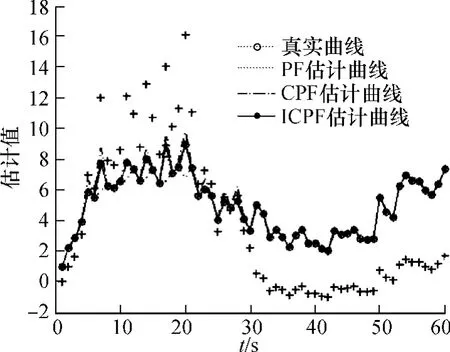
图1 各滤波器的状态估计曲线图

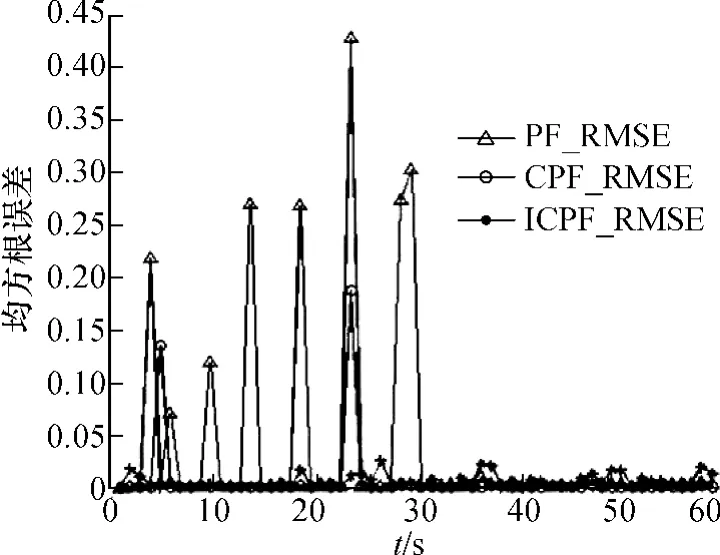
图2 各滤波器均方根估计误差

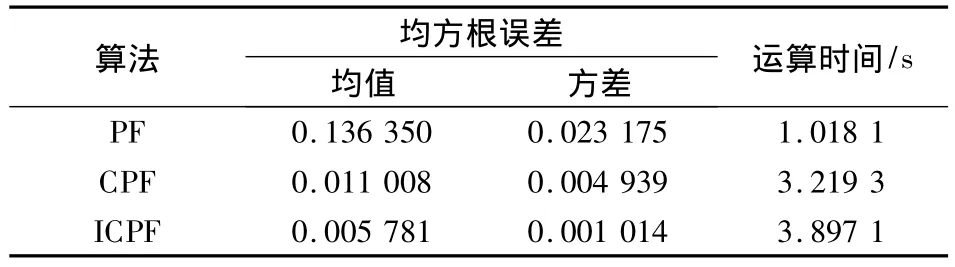
表1 状态均方根误差的均值和方差

通过表1和图2可以看出，由于在ICPF算法中其构造重要性密度函数时，将量测更新后的状态估计值为参考点，对量测方程进行线性迭代处理，使得估计值更加准确，所以ICPF的估计性能明显优于PF和CPF算法.而运行时间上仅仅略高于CPF算法，但跟踪精度得到明显的改善.

4 结论

基于Gauss-Newton迭代思想，提出了迭代容积卡尔曼粒子滤波算法.该算法利用当前量测信息，通过Gauss-Newton迭代方法对CKF算法进行改进，减小线性化误差，以此来产生粒子滤波算法的重要性密度函数，使得迭代CKF产生的重要性密度函数更接近于真实后验概率分布.仿真结果表明ICPF估计效能优于CPF，是一种有效的非线性估计算法.

References)

［1］Gordon N J，Salmond D J，Smith A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation［J］.IEE Proceedings F(Radar and Signal Processing)，1993，140(2):107-113.

［2］Arulampalam M S，Maskell S，Gordon N.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50(2):174-188.

［3］Doucet A，Godsilli S J，Abdrueu C.On sequential Monte Carlo sampling methods for Bayesian filtering［J］.Statistics and Computing，2000，10(3):197-208.

［4］De Freitas N，Niranjan M，Gee A H，et al.Sequential Monte Carlo methods to train neural network models［J］.Neural Computation，2000，12(4):955-993.

［5］李良群，姬红兵，罗军辉.迭代扩展卡尔曼粒子滤波器［J］.西安电子科技大学学报，2007，34(2):233-238.Li Liangqun，Ji Hongbing，Luo Junhui.Iterated extended Kalman particle filtering［J］.Journal of Xidian University，2007，34(2):233-238.(in Chinese)

［6］Van der Merwe R，Douce A，de Freitas N，et al.The unscented particle filter［R］.Cambridge，UK:Engineering Department，Cambridge University，2000:1-45.

［7］郭文艳，韩崇昭，雷明.迭代无迹Kalman粒子滤波的建议分布［J］.清华大学学报:自然科学版，2007，41(S2):1866-1869.Guo Wenyan，Han Chongzhao，Lei Ming.Particle distribution control for an iterated unscented Kalman particle filter［J］.Journal of Tsinghua University:Science and Technology，2007，41(S2):1866-1869.(in Chinese)

［8］Bell B M，Cathey F W.The iterated Kalman filter update as a Gauss-Newton method［J］.IEEE Transactions on Automatic Control，1993，38(2):294-297.

［9］Zhang Jungen，Ji Hongbing.IMM iterated extended Kalman particle filter based target tracking［J］.Journal of Electronics and Information Technology，2010，32(5):1116-1120.

［10］Arasaratnam I，Haykin S.A numerical integration perspective on Gaussian filters［J］.IEEE Transactions on Automatic Control，2009，54(8):1254-1269.

［11］王小旭，潘泉，黄鹤，等.非线性系统确定采样型滤波算法综述［J］.控制与决策，2012，27(6):801-812.Wang Xiaoxu，Pan Quan，Huang He，et al.Overview of deterministic sampling filtering algorithms for nonlinear system［J］.Control and Decision，2012，27(6):801-812.(in Chinese)

［12］Arasaratnam I，Haykin S.Cubature Kalman filters［J］.IEEE Transactions on Automatic Control，2009，54(6):1254-1269.

［13］Arasaratnam I，Haykin S，Hurd T R.Cubature Kalman filtering for continuous-discrete systems:theory and simulations［J］.IEEE Transactions on Signal Processing，2010，58(10):4977-4993.

［14］孙枫，唐李军.Cubature粒子滤波［J］.系统工程与电子技术，2011，31(11):2554-2557.Sun Feng，Tang Lijun.Cubature particle filter［J］.Systems Engineering and Electronics，2011，31(11):2554-2557.(in Chinese)

［15］穆静，蔡远利，张俊敏.容积粒子滤波算法及其应用［J］.西安交通大学学报，2011，45(8):13-17.Mu Jing，Cai Yuanli，Zhang Junmin.Cubature particle filter and its application［J］.Journal of Xi'an Jiao Tong University，2011，45(8):13-17.(in Chinese)