Cramer法则的教与学

王宏兴

（淮南师范学院 数学与计算科学系,安徽 淮南 232038）

1 引言

线性代数是理工类和经管类重要的公共基础理论课程之一。掌握该课程基本概念、基本理论和基本运算方法有助于学生理解代数学的基本思想、培养应用线性代数解决实际问题的能力，也有助于学生的逻辑推理能力、抽象思维能力和数学素养的提高，为后继课程学习打下坚实的基础。

线性方程组的求解问题是线性代数核心问题之一，也是线性代数最早研究的问题。约早在公元前2世纪，《九章算术·方程》就三个未知量的线性方程组的解法作了较完整的论述。类似的方法，1826年为德国数学家高斯 (Carl Friedrich Gauss 1777-1855)创建,简称为高斯消元法。在西方，线性方程组的研究是在17世纪后期由德国数学家莱布尼兹(Gottfriend Wilhelm Leibniz 1646-1716)开创，其在1678年的一份手稿中,给出了所谓Cramer法则的雏形。1748年，英国数学家马克劳林(Colin Maclaurin 1698-1746)在其遗著 《Treatise of Algebra》中给出了该法则。虽然其表达式复杂、符号变化规则模糊,但它在本质上与我们今天所使用的Cramer法则是一致的，甚至有证据表明马克劳林在1729年就知道并教授其学生学习该法则。1750年，瑞士数学家克莱姆(Gabriel Cramer 1704-1752)在其专著 《Introduction to the Analysis of Algebraic Curves》一书中研究一条代数曲线上已知点的坐标与该曲线方程系数的关系时给出了Cramer法则。

定理1：（Cramer法则）对于n各变量，n个方程的线性方程组

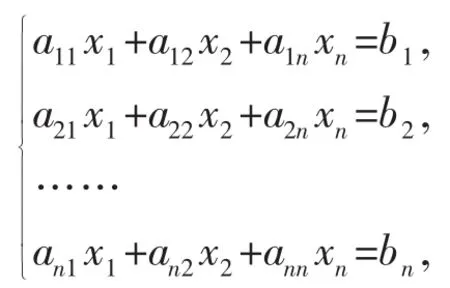
如果它的系数矩阵是可逆的detA≠0，则它有唯一解

由上述的定理我们知道应用Cramer法则的条件是：方程的个数等于未知量的个数，系数矩阵是实数域上n阶可逆矩阵；Cramer法则的结论是：方程有解，解唯一，解的表达式。

克莱姆给出的表达式简洁、优美，堪称符号化的一个典范，受到广泛高度的赞赏，被认为是线性代数诞生的标志。这也是马克劳林和莱布尼兹比克莱姆更早的发现、使用所谓的Cramer法则，但是习惯上把Cramer法则归属于克莱姆的主要原因之一。

上述定理也可以等价地描述为以下的形式：

定理1’：（Cramer法则）设A是实数域上n阶可逆矩阵，则对实数域上任意的n维列向量b，线性方程组Ax=b有唯一解，且

其中x1表示唯一解x的第i个分量，记号A(i→b)表示列向量b代替矩阵A的第i列后得到的矩阵。

例题：已知二次曲线y=f(x)=a0+a1x+a2x在三个点x±1,x=2处的值为f(1)=f(-1)=3,f(2)=3。试求系数a0,a1,a2。

解：由已知条件有：

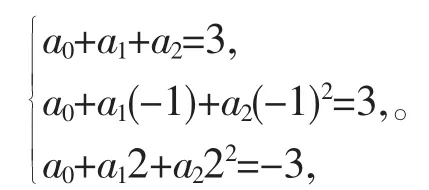
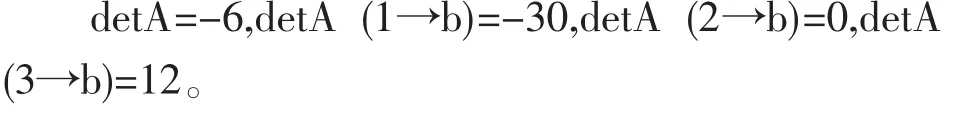
应用Cramer法则，有a0=5,a1=0,a2=-2。

2 Cramer法则的证明

Cramer法则是线性代数中重要的知识点之一。虽然该方法计算量大，但是其给出了解与系数的明显关系，并且其表述方式简洁、优美。遗憾的是，克莱姆本人没有给出Cramer法则严格的理论证明。Cramer法则的首个证明是法国数学家柯西(Augustin-Louis Cauchy 1789-1857)在1815年给出的。以下我们简述三种关于Cramer法则的证明方法，从这些方法中我们可以看到新的证明是如此的精致、巧妙和初等。

首先简述一种线性代数教材上给出的证明方法。这个证明方法应用了伴随矩阵、矩阵逆的表示、矩阵乘法以及行列式展开等知识。

证法1①同济大学数学教研室：《工程数学:线性代数》，北京:高等教育出版社,1999年，第29-30页。：由于A是可逆矩阵，令x=A-1b，则有Ax=AA-1b=b。即x=A-1b是线性方程组Ax=b的解。由Ax=b，有A-1Ax=A-1b，即x=A-1b。由矩阵逆的唯一性，我们有x=A-1b是方程组的唯一解。

我们记A*为A的伴随矩阵。由矩阵逆的表达式

有

也就是说 xi=detA(i→b)/detA,i=1,2,…,n。

1970年S.M.Robinson在文[2]中引入的记号A(i→b)表示列向量b代替矩阵A的第i列后得到的矩阵。也就是说，如果我们记ai表示A的第i列，A的列分块为 ，则有

下面的证明是S.M.Robinson在文[2]中应用该记号给出的关于Cramer法则的一个漂亮证明。

证法2②S.M.Robinson,A short proof of Cramer’s rule,Math.Mag.1970，No.43,pp94-95.：我们记E为单位矩阵。由于Ax=b可以等价地表示为

由行列式的可乘性知

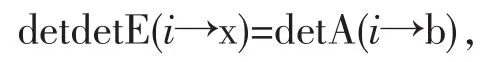
以及

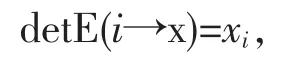
即得

1992年A.Ben-Israel给出该法则的一个新的证明方法③陈永林：《广义逆矩阵的理论与方法》，南京：南京师范大学出版社,2005年，第202-226页。。这个证明不用行列式的可乘性，只用到了行列式的基本性质：记矩阵A的列分块为A=(a1,…,ai-1,ai+ai′,ai+1,…,an)，则

也就是说，如果一个行列式的某一列是两组数的和，那么这个行列式就等于两个行列式的和，而这两个行列式除这一列外与原来行列式的对应列一样。

证法3：记ai表示A的第 列，xi表示唯一解x的第i个分量。由于

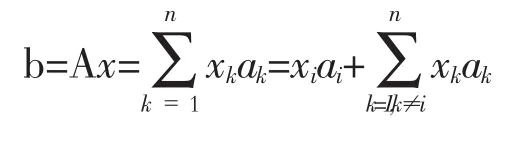
则有：

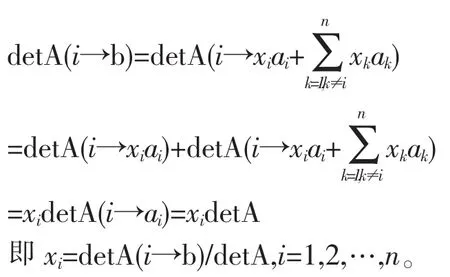
注：由于证法3只用到了行列式的基本性质，所以我们认为该证明方法较证法1和证法2更初等。

3 Cramer法则的推广

我们有时候也称克莱姆在1750年发表的Cramer法则为古典Cramer法则。在应用古典Cramer法则时我们首先需要确定方程的系数矩阵是实数域上阶可逆矩阵，其应用范围有限。1982年，A.Ben－Israel研究该法则在相容矩阵方程最小范数解上的应用，开创了古典Cramer法则在更大范围应用研究的先河。

定理2①A.Ben－Israel,A Cramer rule for least-norm solutions of consistent linear equations,Linear Algebra Appl.43(1982),pp223－226.：设矩阵A是实数域上m×n矩阵，b是实数域上m维列向量，rank(A,b)=rank(A)，则Ax=b的最小欧氏范数解x的第j个分量为

其中U,V记号的意思与文②A.Ben－Israel,A Cramer rule for least-norm solutions of consistent linear equations,Linear Algebra Appl.43(1982),pp223－226.相同。

其后，国内外众多学者继续研究了古典Cramer法则在约束矩阵方程、约束线性方程组、广义逆矩阵等问题上的应用③H.J.Werner,On extensions of Cramer’s rule for solutions of restricted linear systems,Linear and Multilinear Algebra 15(1984)319－330.－⑦J.Ji,A condensed Cramer’s rule for the minimum-norm least-squares solution of linear equations，Linear Algebra Appl.437(2012),2173－2178.以及交换环上的Cramer法则、四元数除环上的Cramer法则⑧⑨T.Jiang,Cramer rule for quaternionic linear equations in quaternionic quantum theory，Reports on Mathematical Physics,57(2006),463－468.等。

2002年，Z.Gong,M.Aldeen和 L.Elsner给出广义Cramer法则的研究。

定理3⑩Z.Gong,M.Aldeen,L.Elsner,A note on a generalized Cramer’s rule,Linear Algebra Appl.2002 年第340卷，第 253－254页。：（广义Cramer法则）设A是实数域上m×n可逆矩阵，X,Y是实数域上n×m矩阵，且满足AX=Y，则

其中 1≤i1〈i2〈…〈ik≤n，1≤j1〈j2〈…〈jk≤m，X]表示由 X 的 i1,i2,…,ik行，j1,j2,…,jk列构成的k阶子矩阵，]表示A的i1,i2,…,ik列依次被Y的j1,j2,…,jk列代替后后得到的矩阵。

当m=1时，上述定理就是我们常说的古典Cramer法则。

更多关于Cramer法则的研究及其应用可以参考文⑪等等。

4 结束语

本文主要讲述Cramer法则的发展历史、应用、证明方法、推广以及最新研究成果。授课教师可以有选择地对上述证明、定理等加工利用。特别是在对高年级本科生讲授Cramer法则时，这些证明方法和研究成果的介绍能更吸引学生的注意力、增强学生对Cramer法则乃至线性代数这门课程的兴趣，也对他们后继学习、科研具有一定的参考价值。