微分中值定理的推广与应用
2013-08-14程娜
程 娜
辽宁广播电视大学 (沈阳 110034)
1 中值定理的内容及联系
1.1 基本内容
1.1.1 Rolle定理
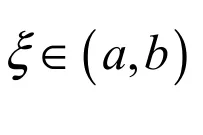
1.1.2 Lagrange定理
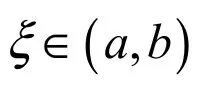
1.1.3 Cauchy定理
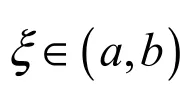
1.2 三个定理之间的联系
对这三个定理进行观察和类比,从中可以发现这三个定理条件和结论都很相似,通过改变条件还可能互相转化。从而我们可以得出这样的结论:拉格朗日(Lagrange)定理是罗尔(Rolle)定理的推广,而罗尔(Rolle)定理是拉格朗日(Lagrange)定理的特例,拉格朗日(Lagrange)定理是柯西(Cauchy)定理收缩,而柯西定理则是拉格朗日定理的推广。
2 定理的推广
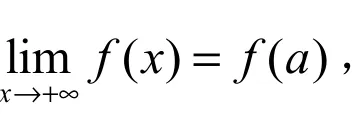
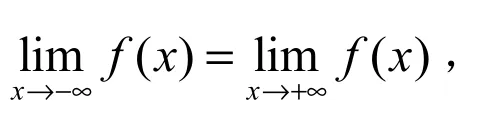
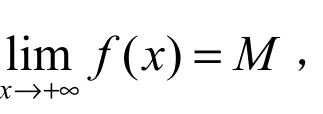
3 定理的应用
3.1 利用微分中值定理来证明不等式
例 设函数 f( x)在[0,1]上连续,在(0,1)内可导,且f( 0)= 0 ,f( 1)= 1 。试证:对任意给定的正数a, b在(0,1)内不同的ξ,η
又由于 f( x)在[0,1]上连续且 f ( 0)= 0 ,f ( 1)= 1 。由介值性定理,∃ τ ∈ ( 0,1)使得
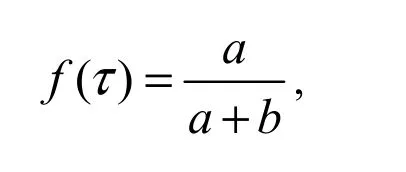
f( x)在[0,τ],[τ,1]上分别用拉格朗日中值定理有
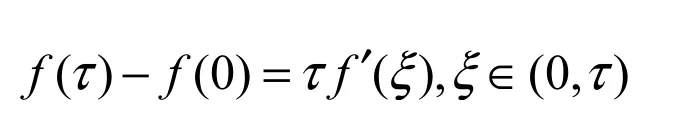
即
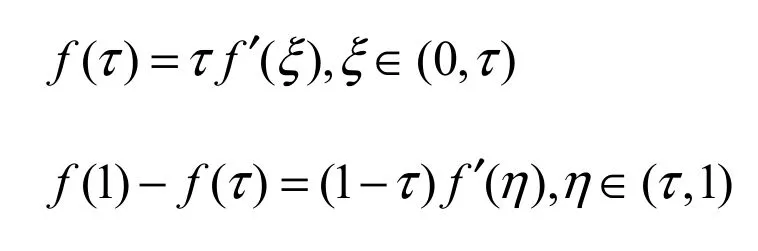
即
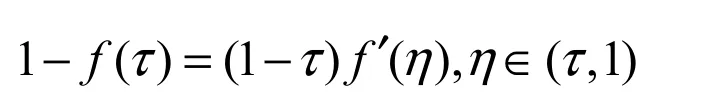
于是由上面两式有
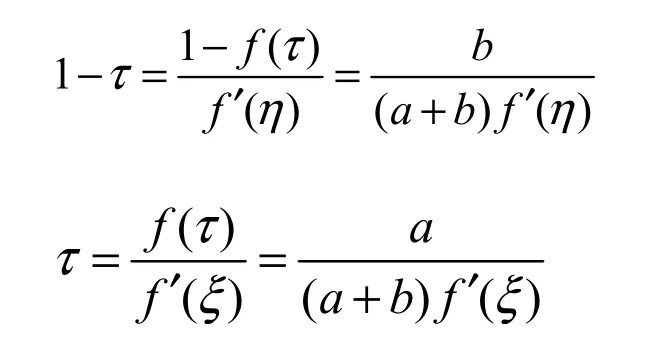
将两式相加得
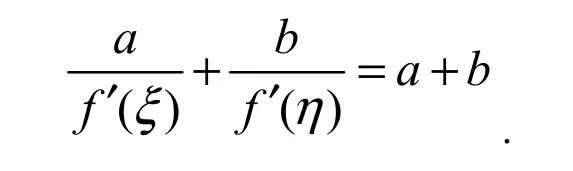
3.2 用微分中值定理求极限
解:根据题意,由Lagrangge定理,有
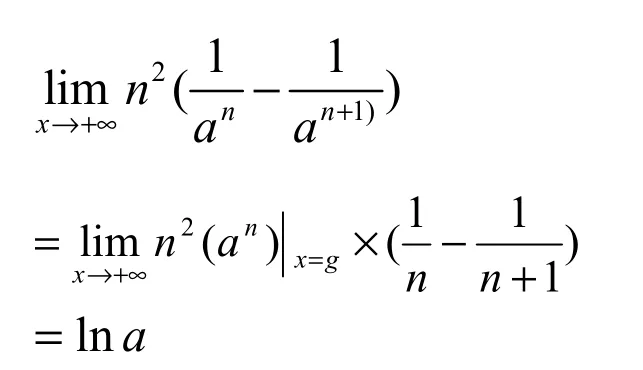
3.3 利用定理证明方程根(零点)的存在性
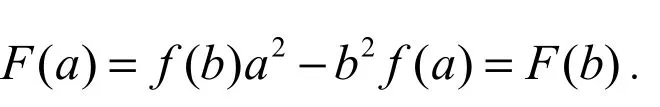
对微分中值定理的研究和应用从微积分建立之初就开始了,本文从三个方面介绍了该定理的运用。通过以上的例题让大家了解,运用中值定理的关键和解题的难点,是在于构造辅助函数。对微分中值定理本课题主要是以罗尔定理、拉格朗日定理和柯西定理,三个定理之间的联系为主要的研究对象,希望通过本篇文章能够使大家对微分中值定理的内容更加深刻了解,同时在应用中值定理时更加熟练。
[1]华东师范大学数学系编.数学分析第三版[M].北京:高等教育出版社,2001.
[2]孙清华,孙昊编.数学分析内容、方法与技巧(上)[M].武汉:华中科技出版社,2003.
[3]北京邮电大学数学教研室,高等数学[M].北京:北京邮电在学出版社,2003.
[4]同济大学应用数学系,高等数学[M].北京:高等教育出版社,2002.
