正交小波变换的开关电流电路实现*

胡沁春

(成都工业学院 电气与电子工程系，四川 成都 611730)

小波变换可以在多尺度上对信号进行分解，并同时在时域和频域上具有较好的局部化特性。这种优异的时频分析特性使得小波变换成为分析非平稳和瞬变信号的强有力工具，在信号检测、特征提取、语音分析、图像处理、模式识别、故障诊断和定位、数据压缩等领域取得了良好的应用[1]。开关电流电路是基于电流模的电路，它用离散时间的取样数据系统处理连续时间的模拟信号，具高频特性好、低电压、低功耗、动态范围大等优点[2]。在利用小波变换对信号进行处理时，为了保证原始信号域和变换域分析的一致性，往往需要按某种方式可以完全重建信号的小波变换，最完美的一种解决方案就是正交小波变换。如果小波函数是正交的，则信号重构可以用多分辨分析理论来进行，否则必须用小波级数与小波框架理论来进行信号重构[1]。本文对Laguerre结构进行研究，根据正交小波变换的Laguerre结构实现方案，提出正交小波变换的开关电流电路实现，便于其被制成符合最新数字工艺的集成芯片。

1 Laguerre结构

小波分析的Laguerre结构采用的是延迟算子的级联，它实际上是一个存储器[3]。扩展 Laguerre结构，使结构不同节上的冲激响应是同一个尺度函数φ(t)的扩展；然后采用多尺度Laguerre存储器，在不同的分辨率上对信号f(t)生成逼近式。图1为k阶Laguerre存储器的结构。

图1 k阶Laguerre存储器的结构

从图1可以看出，k阶Laguerre存储器由一个一阶低通节和一个k-1阶的全通节的级联构成。k阶Laguerre存储器的频率响应为[3]：

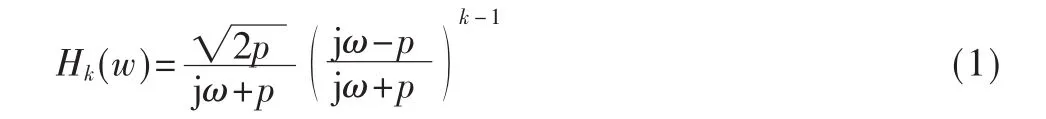
其中，p和-p是第k-1个零点以及第k个极点的位置。这种结构被拓展成为多尺度Laguerre存储器。k阶Laguerre 存储器 Un0，k(ω)在频域的定义是：

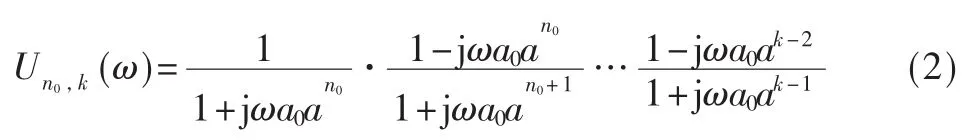
其中，a＞1，且极点被因子a成指数间隔开。在拉普拉斯域的低半 平面 内，当 k2＞k1且 s ∈Z 时，的乘积无极点，从而这两个函数就是互相正交的。因此函数 Un0，k(ω)是一系列的正交基函数。设 Hak(ω)有如下的形式：

此时有：

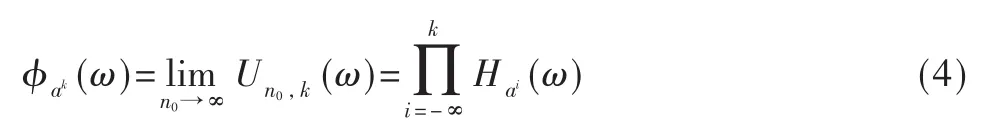
并且有：

两尺度关系直接表示如下：

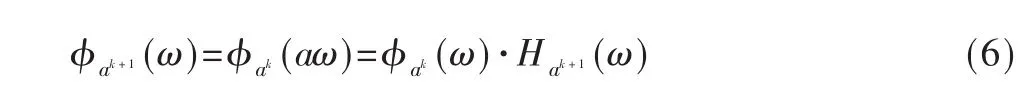
可用多尺度Laguerre存储器来分解信号f(t)并完成正交小波分析。

2 正交小波变换的开关电流电路实现

在图1所示的Laguerre多分辨率分析结构中，低通滤波器用来对信号进行预处理，全通滤波器由式(3)定义。采用开关电流技术，由开关电流一阶节实现Laguerre所需的低通滤波器和全通滤波器。

开关电流通用一阶节如图2所示，图2中J为单位电流 源 ，a0、a1、a2为系数，其设计与实现可见参考文献[4]。考虑将Laguerre正交小波用于音频信号的处理，而工作频率一般在10 kHz以内，因此这个频率范围足以满足实际需要，其时钟频率设定为100 kHz。ASIZ(Analysis of Switched-current Filters in Z Transform)[5]是开关电流电路的专用仿真软件，其可对开关电流电路仿真获得频率响应、极点和零点、瞬态响应和灵敏度等。本文利用ASIZ对开关电流低通节、全通节进行电路仿真。

图2 开关电流一阶节电路

2.1 开关电流低通节的实现

对于低通节，采用图2所示结构，其ASIZ仿真所用的电路如图3所示。图3中与各晶体管相接的电流源应ASIZ仿真要求而省略(输入信号源除外)。开关电流低通节中各晶体管的宽长比值见表1。

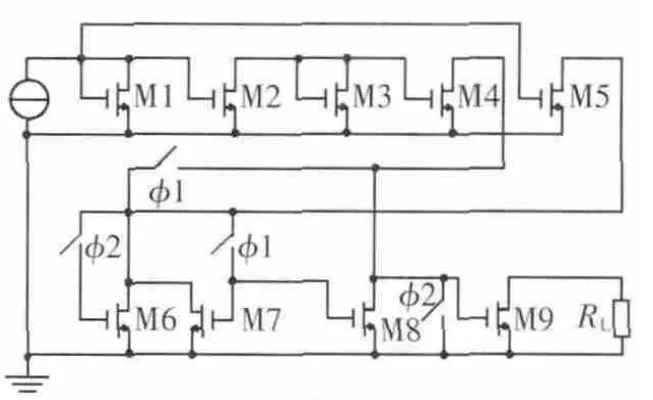
图3 开关电流低通节仿真电路图

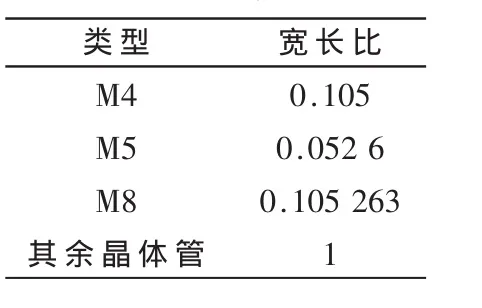
表1 开关电流低通节晶体管宽长比

经过ASIZ仿真，其频率特性如图4所示。从ASIZ仿真结果看出，所设计的开关电流低通节完全满足Laguerre结构实现正交小波分析前级预处理的要求。

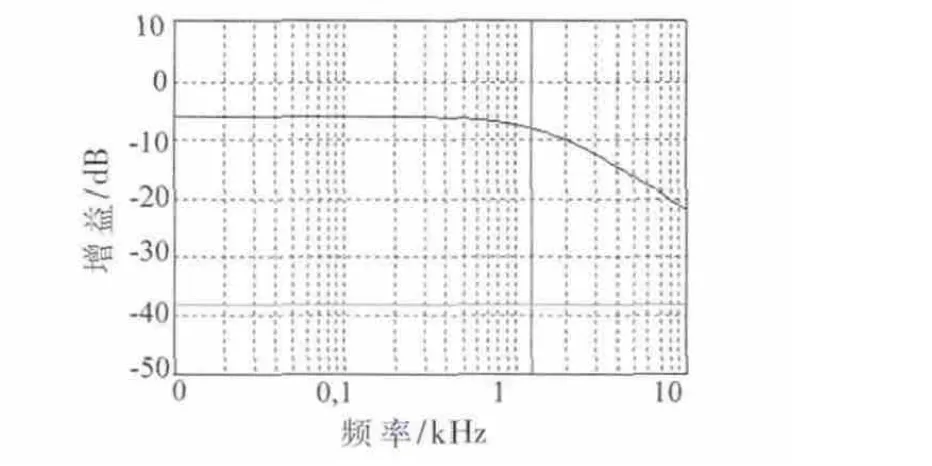
图4 ASIZ仿真开关电流低通节的频率特性

2.2 开关电流全通节的实现

对于Laguerre结构实现正交小波分析所需的全通节，其实现方法同开关电流低通节的实现。其ASIZ仿真所用的电路如图5所示，图5中与各晶体管相接的电流源应ASIZ仿真要求而省略(输入信号源除外)。开关电流全通节中各晶体管的宽长比值见表2。

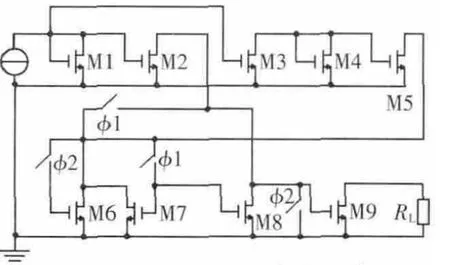
图5 开关电流全通节仿真电路图

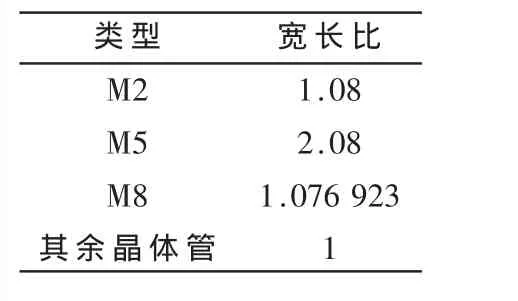
表2 开关电流全通节晶体管宽长比

经过ASIZ仿真，开关电流全通节频率特性如图6所示。

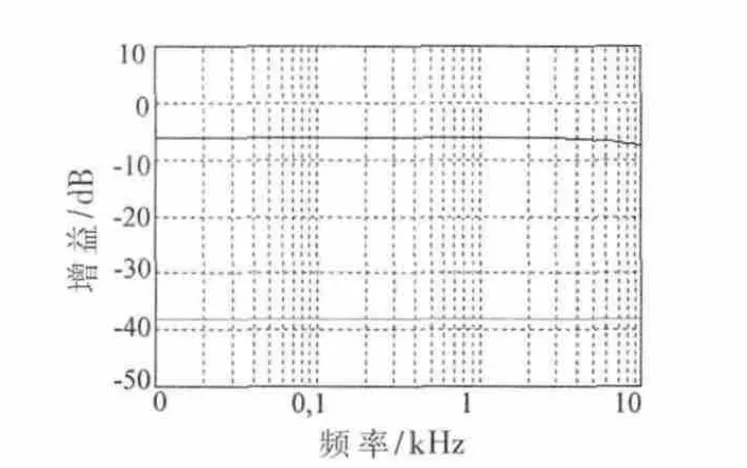
图6 ASIZ仿真开关电流全通节的频率特性

从ASIZ仿真结果看，在0 Hz～10 kHz的工作范围内，开关电流全通节的增益在6 kHz内衰减很小，在6 kHz～10 kHz区间大约有0.5 dB的衰减。经过分析认为是频率翘曲效应所致。将时钟频率提高到200 kHz，得到图7所示的频率特性图。图7中所示开关电流全通节增益在整个工作范围内稳定，可以满足Laguerre结构实现正交小波变换的要求。

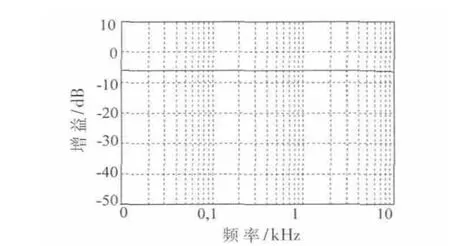
图7 全通节在时钟为200 kHz时的频率特性

3 仿真试验

对信号进行小波分解，其实质就是将信号分成两个信号，即高频部分和低频部分。通常，信号的低频部分包含了信号的主要信息，高频部分则包含了信号的细节信息。根据分析的需要，可以继续对所得到的低频部分进行再分解，如此又得到了更低频率部分的信号和频率相对较高部分的信号。这种方法把—个混频信号分解为若干个互不重叠的频带中的信号，这样就可以完成滤波或检波的工作，达到提取信号特征的目的。

对Laguerre结构实现正交小波变换进行仿真。在完成低通节和全通节电路实现与仿真的基础上，用Matlab对其进行系统级仿真。原始仿真信号为复合正弦信号，由一个频率为10 Hz的正弦波(低频成分，其电流幅值设定为10 mA)和一个频率为1 kHz的正弦波(高频成分，其电流幅值设定为2 mA)构成。用Laguerre结构对该复合试验正弦信号进行正交小波分析，得到的仿真结果如图8～图10所示。图8为原始仿真信号；图9为原始仿真信号通过Laguerre结构后的输出信号，这时信号仅剩下原始仿真信号的低频成分，得到了原始仿真信号的概貌逼近；图10为原始仿真信号与通过Laguerre结构后的信号的差值，其频率较高，是原始仿真信号的高频成分，也即是原始仿真信号的细节逼近。

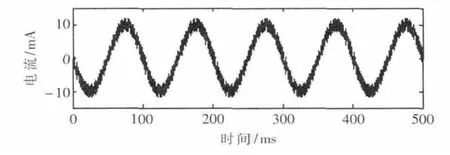
图8 原始仿真信号

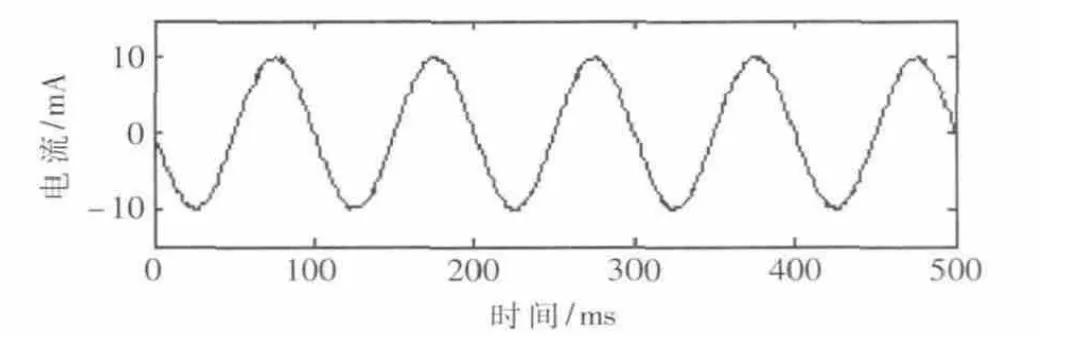
图9 原始仿真信号通过Laguerre结构后的输出信号

图10 原始仿真信号与Laguerre输出信号的差值

正交小波变换是完全重建信号的小波变换中最完美的一种解决方案。为实现正交小波变换，本文对Laguerre结构进行了研究，并采用开关电流技术实现了Laguerre结构中的关键部件——低通滤波器和全通滤波器，从而为实现高速、低电压、低功耗的小波变换电路提供了新的途径。同时用ASIZ对开关电流低通滤波器和开关电流全通滤波器进行了仿真，其结果理想，并进一步用Matlab对Laguerre结构进行了系统级仿真。仿真结果表明，用Laguerre结构实现正交小波变换是可行的。

[1]STEPHANE M.A wavelet tour of signal processing(Third edition：the sparse way)[M].New York：Academic Press，2008.

[2]TOUMAZOU C，HUGHES J B，BATTERSBY N C.开关电流—数字工艺的模拟技术[M].姚玉洁，刘激扬，刘素馨，等译.北京：高等教育出版社，1997.

[3]Chen Dongwei，HARRIS J G.An analog VLSI circuit implementing an orthogonal continuous wavelet transform[C].1998 IEEE International Conference on Electronics，Circuits and Systems，Lisbon，Portugal，07-10 Sep，1998：139-142.

[4]胡沁春，郭迪新.开关电流滤波器的设计与实现[J].湖南工业大学学报(自然科学版)，2009，23(1)：92-95.

[5]De Queiroz A C M，PINHEIRO P R M，CALOBA L P.Nodal analysis of switched-current filters[J].IEEE Transactions on Circuits and Systems II：Analog and Digital Signal Processing，1993，40(1)：10-18.