软土地基最终沉降量推算方法的对比分析

2013-08-13王荣利秦观刘洪亮

中国港湾建设 2013年2期

王荣利，秦观，刘洪亮

（1.中交天津港湾工程研究院有限公司，港口岩土工程技术交通行业重点实验室，天津市港口岩土工程技术重点实验室，天津 300222；2.中交第一航务工程局有限公司，天津 300451）

目前国内一般采用三点法、经验双曲线法、高木俊介法来推算地基固结度。三点法计算简单，存在一定的随机性，在满载后沉降曲线段中，选择不同的时间区段或者不同的时间间距，对推算最终沉降量的结果都有明显的影响，推算最终沉降量的离散性大，确定地基的最终沉降量存在很大的随机性，不能作为精确推算使用。

本文以科威特巴比延岛试验段路基处理为基础，运用经验双曲线法、高木俊介法、ASAOKA法进行最终沉降量计算分析，论证了更为适合科威特巴比延岛地质条件的经验计算方法。

1 工程概况

科威特巴比延岛路堤地基加固是一个挑战，以往从未在该岛进行过软基加固，科威特本国的科研单位在这方面也缺少研究。另一方面，设计文件又对地基处理的工后沉降提出了较高的要求，即施工结束后1 a内的沉降小于25 mm。这样高标准的工后沉降指标给地基加固技术提出了较高的要求。

科威特巴比延岛软基处理试验段采用堆载预压处理方式，试验区面积为340 m×80 m，排水板深度为17 m，间距为1.2 m，三角形布置。路堤结构部位按照使用结构荷载（沉降盘SP3、SP8、SP13、SP18断面对应堆载厚度分别为2.2 m、2.5 m、2.8 m、3.1 m）施加后超载3 m粉土，属超载预压处理。整个试验区布置了4个断面共计20个沉降盘，进行了400 d的沉降观测，得到了比较稳定的沉降观测值，以下所进行的计算分析均以实际观测资料为基础。

2 地质情况

科威特巴比延岛是一个三角洲形岛屿，系由幼发拉底河和底格里斯河系统进入阿拉伯湾之后所携带的泥沙沉淀形成的。岛的表面十分平整，在高水位时会被淹没。岛的地层可以分成2层：

第一层：深度为18～25 m，主要是软黏土到灰硬黏土或粉土，一般为钙质夹杂着有机物。局部有黏土和粉土层。由于旱季脱水及盐结晶作用，在上部的1～2 m的范围内为氧化后的褐色粉质黏土。该层是近期（全新世）最后一次冰河期结束后环境激烈变化时形成的，冲刷材料在幼发拉底河和底格里斯河末端进入阿拉伯湾时发生沉淀。因此该层主要为细粒、松软，包含有机物和来自于生长在河流和海湾的生物的钙质材料。

第二层：第一层以下为中等密实和非常密实的细砂到中砂，一直到钻孔揭露的最大深度35 m。在岛的中部和东部25 m以下遇到了坚硬的含砂黏土，局部也有坚硬的黏土。该层形成的时间更加古老，大约为更新世，在这期间河流和海湾的粗料沉淀下来。这些材料已经有足够的时间固结，并且受到河流和河口作用导致表面起伏较大。

科威特巴比延岛路堤试验段区域土质为低塑性和中等塑性黏土，软土深度16 m，比贯入阻力qc＞0.85 MPa，竖向固结系数平均值为4 m2/a，压缩指数平均值为0.23，孔隙比平均值为0.843。

3 方法及应用分析

3.1 经验双曲线法及应用

依据《港口工程地基规范》中“经验双曲线”公式，对本项目的4个断面的中心点沉降盘沉降进行双曲线公式计算，其中SP8拟合曲线见图1，其余沉降盘规律一致。

图1 SP8沉降盘经验双曲线法拟合曲线

由经验双曲线公式计算的最终沉降量如表1所示。

表1 经验双曲线计算最终沉降值

从图1曲线分析看，拟合线与实测线的相关性很高，相关系数平方值均可达到0.996以上，拟合线和实测线相关明显，线性的选择是合理的。但是经验双曲线法需要选择合理的时间推算点，且不能计算主固结沉降量及次固结沉降量大小，对于此工程不能准确推算卸载时间。

3.2 高木俊介法及应用

依据JGJ 79-2002《建筑地基处理技术规范》的高木俊介公式，根据试验段的地质资料及排水板的施工相关参数，并考虑涂抹和井阻的影响，运用公式计算并模拟沉降曲线。对本项目的4个中心点沉降盘沉降运用高木俊介公式计算，其中沉降盘SP8计算结果如图2所示，其余沉降盘规律一致。

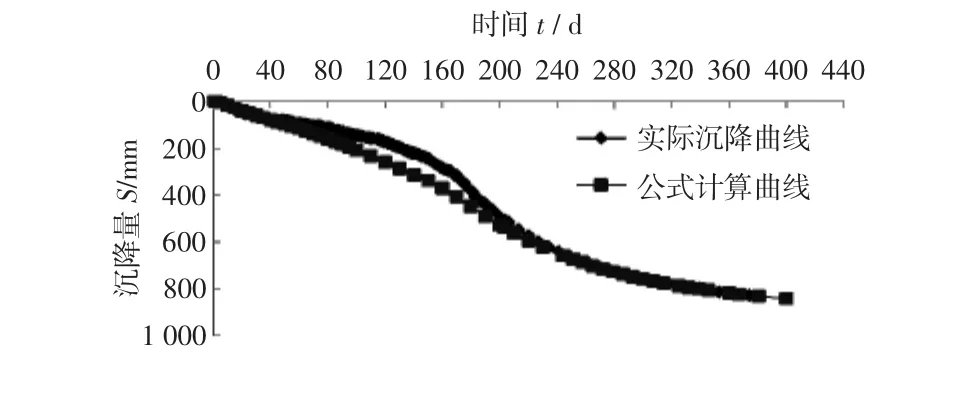
图2 SP8沉降盘高木俊介公式曲线图

由高木俊介公式推算的最终沉降量如表2所示。

表2 高木俊介公式推算最终沉降值mm

从图2分析来看，满载期后的实测沉降曲线与公式计算曲线相关性比较好。高木俊介公式主要利用试验数据对实测沉降进行沉降曲线模拟，并调整土质的固结系数、压缩系数等相关参数，稳定后与试验室提供数据进行比较，判断不同土质条件下实际沉降反算的参数与试验室参数的差异，分析该区域土质的涂抹及井阻对排水固结的影响。另外高木俊介公式不能计算主固结沉降量及次固结沉降量大小，并且需要前期的大量数据作为基础，才能进行相关推导计算。

3.3 ASAOKA法及应用

3.3.1 ASAOKA法简介

ASAOKA法是根据相关公式提出的一种图解法。其步骤如下：

1）以工程满载后开始，以ρj-1为x轴，以ρj为y轴，j为截取的某时间点，将各沉降值ρ1，ρ2…（均为相等的时间间隔对应沉降量）的点（ρj-1，ρj）在图中画出，同时作出ρj-1=ρj的45°直线，如图3所示。

图3 ASAOKA法分析图

2）做直线（1）与这些点吻合，直线（1）与45°直线相交的点所对应的沉降量ρj即为最终沉降量。倾斜角β1表示沉降速率。

当观测时间较长时，由于主固结沉降全部完成，次固结沉降发生作用时，直线会出现斜率变化点，此时会出现两条直线（1）和（2）与数据相吻合的情况，如图4所示，直线（1）表示主固结沉降阶段的总沉降，直线（2）表示次固结沉降阶段的总沉降。

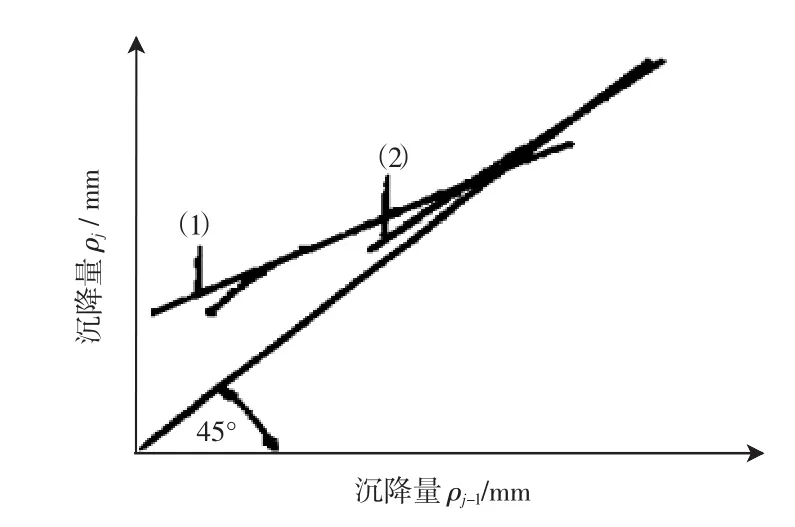
图4 主固结沉降段及次固结沉降段总沉降直线

3.3.2 ASAOKA法应用

对本项目的4个中心点沉降结果采用ASAOKA法进行计算，分别得出主固结沉降段及次固结沉降段总沉降，其中沉降盘SP8计算结果如图5所示，其余沉降盘规律一致。

由ASAOKA法推算的最终沉降量如表3所示。

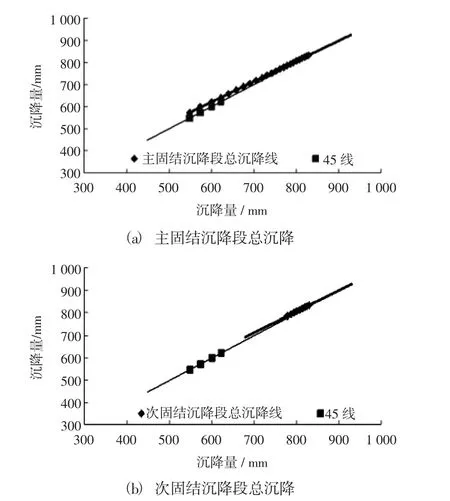
图5 SP8沉降盘ASAOKA法推算沉降值曲线

表3 ASAOKA法推算最终沉降值mm

由表3结果可以看出，ASAOKA图解法更为简洁，所需数据可以为满载后某一阶段性数据，并能更进一步计算包含次固结沉降下的最终沉降量，提供加固后的残余沉降量数值，为路堤卸载时间提供准确的数据。

3.4 对比分析

综合以上3种推算方法的数据，汇总得出表4。

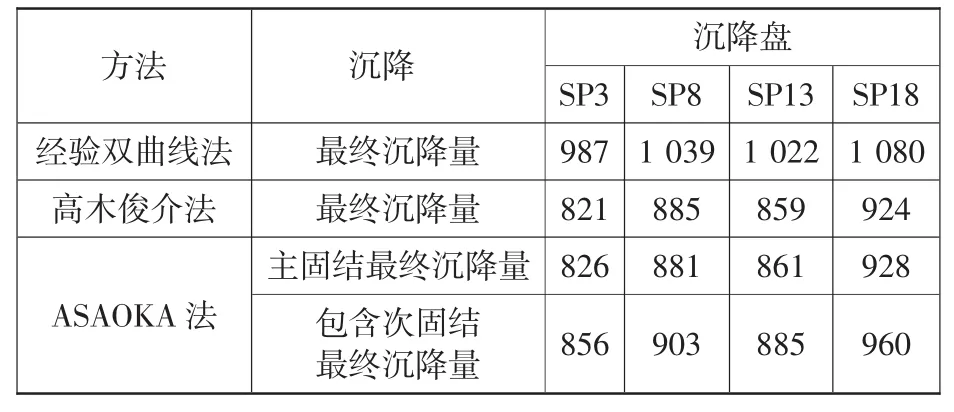
表4 三种计算方法的结果比较分析mm

综合上述3种方法，由表4数据可以看出，经验双曲线法的最终沉降量结果比其它两种方法的沉降量偏大约143 mm，而高木俊介公式及ASAOKA法推算的主固结沉降量平均偏差为2 mm。分析经验双曲线法推算沉降量偏大原因为：一是科威特巴比延岛地质条件与国内施工的极软地质不同，总沉降量相对国内淤泥质地质条件较小；二是经验双曲线法运用最小二乘法原理，通过控制均方根误差最小来实现的，实际拟合时，不同的曲线方程推算的最终沉降量有一定的误差。

高木俊介公式计算过程需要前期试验提供大量的地质资料和土质参数，运用公式计算沉降曲线并与实测曲线进行拟合，整个过程需调整土质的相关参数。

ASAOKA图解法可以选用满载后的任意较短时间观测资料，对沉降过程的阶段性依赖不明显，并且能够推算出次固结沉降量大小，为后期施工使用提供可靠的数据参考，实用性比较强。