桥梁施工安全事故流变－突变规律

2013-08-11杨伟军杨永达

土木与环境工程学报 2013年1期

杨伟军，王鹏，2，杨永达

（1.长沙理工大学土木与建筑学院，长沙410076；2.中铁十一局集团，武汉430062）

近年桥梁安全事故频发，支架坍塌后果最为严重，对人民的生命和财产安全造成巨大损害，桥梁施工安全问题再次引起广泛关注。施工安全事故的种类较多，应结合施工生产特点从分析安全事故的特点着手，掌握事故发生规律，着重分析影响较大、伤害较大、损害较大、发生较频繁的安全事故［1－2］。在施工生产中，有些事故类型出现较多，尤其是坍塌事故占的比例较大。表1统计了近几年全国施工安全事故坍塌事故所占的比例。

表1 施工安全事故坍塌事故所占的比例

桥梁施工安全风险分析的根本目的是为了防止安全事故的发生。因此在进行风险分析前，应该对安全事故的致因及其发生过程有深刻的认识，从而能够对导致安全事故发生的危险源、影响程度等进行全面的辨识和评价［3］。通过大量工程实践积累，结合施工特点，利用科学的方法找到事故规律，深刻认识事故致因和过程。文章结合这一特点，从事故触发过程方面来研究施工安全事故致因。

1 桥梁施工事故流变突变基本规律

当前常用的全事故致因理论有轨迹交叉论和能量转移论进行致因分析时［4－6］，前者缺少对环境系统的分析，且偏重于管理角度，而缺少控制方法。后者在分析具体事故时较为有效，但无法明确能量转移路径和具体能量值。要进行桥梁施工过程安全事故致因理论的研究，首先应该明确安全事故在施工过程中表现是突发的，但其根源是各种因素和条件的结合。从事故发生过程来看，表现出各种潜在风险因素量的积累，最终变成事故，即事故本身是实质上的流变和形式上的突变。

从目前关于流变突变理论的研究可见，施工事故的发生同样存在流变突变特征。对事故过程进行该理论的分析不仅可以客观的解释事故发生原因，也可以作为对事故本质原因挖掘的基础［7－10］。但和一般的流变突变规律有所不同，桥梁施工安全事故的发生更容易显现出突变性，而流变性不容易被察觉，这也是对其进行流变突变研究的必要性所在。在安全事故中，人员伤亡或者结构坍塌是标志事故发生的主要特征，如果用安全度来表示事故发生过程中的人员或结构的状态，那么按照流变突变理论，在事故经过时间内，随着时间增加安全度逐渐降低，而影响安全度随时间变化的因素就是事故致因。

对于桥梁施工过程，不安全度为0的时候是不存在的，这也是流变突变普通规律图中所存在的缺陷，且安全事故的发生和一般系统的不同在于流变时间并不是很长。若施工过程中隐含了不安全因素，即为施工过程中的防护不足、自身抗力不足或自身外力过大，此时施工系统安全度会逐渐降低，根据流变突变理论可以绘制其近似的规律图如图1所示。

图1 桥梁施工安全事故流变规律曲线

图1所示曲线中DS为安全度，横轴为事故从风险因素作用到最终发生的时间t。当施工过程中的风险因子开始作用时后，施工系统安全度随时间到t1时，从初始的DS0开始缓慢降低，降到DSA后开始快速下降，施工系统即将发生事故，当安全度DSC突破后，事故已经发生，到DSD时已降到最低状态，事故过程完成。采用流变突变规律曲线进行桥梁施工安全事故过程分析只能定性的进行事故发生过程描述，因此可对曲线规律进行一些数学模型上的研究从而找到更深层次的原因和规律。

2 桥梁施工安全事故流变突变数学模型

当施工系统在事故发生过程中按照图1曲线变化时，曲线斜率代表安全度下降量和时间的比值且小于0。令系统安全度DS∈（0，1），这里取开区间是因为实际中并不存在绝对安全和绝对不安全。与安全度反对应的是危险度DU，若系统总度为1，则有

引入系统衰减率来表示单位时间内安全度下降量与安全度的比值，因此可以假设安全度衰减率为η，η是系统安全度DS和时间t的函数。当t＝t0时，从图1中可知施工安全度为DS0，是系统中最大的安全度，此时η＝0，对应的危险度为1－DS0。随时间增长，安全度越来越小，则η越来越大，最终出现安全事故。借助衰减率，安全度和时间的关系可表示为

对于曲线斜率的变化受衰减率和安全度影响，DS（1－DS）可以理解为施工系统对安全度下降的阻滞作用，而η则代表了衰减趋势。这种观点和传统的流变突变理论中安全阻尼件、安全可逆件等元件作用原理是吻合的。结合曲线特征，按照流变突变理论，将事故过程分为三个过程，假设在t1－t3之间的某时刻t处有dDS／dt＝－1。

则代入式（2）可以得到

根据反LOG函数曲线特征和已知式（2）和（3）可得到DS随时间变化函数为：

根据式（1）的设定，以及t0时刻为起始时间，设为0，式（4）可以简化为：

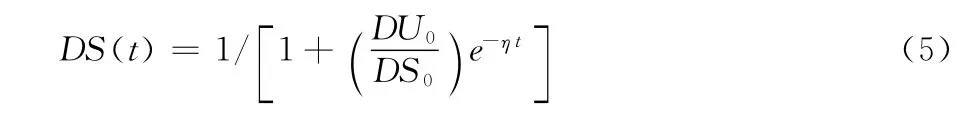
图1中T为事故全过程时间，当事故到达事故结束时间T时，施工系统安全度降到最低DSD。则事故时间T为：

对于桥梁施工而言，安全事故发生时间一般是比较短暂的，因此对式（6）事故时间T的理解应该是将事故时间分为N个无量纲的细小步距，t为不同细小单元时间对总时间的比值，若将时间以t／T进行表示，则可以得到桥梁施工安全事故流变突变模型为：

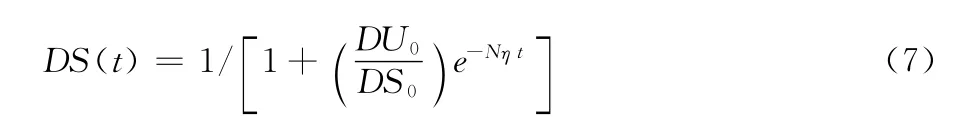
其中，N为常数。

3 基于流变突变数学模型的事故致因分析

3.1 事故致因与流变突变曲线的关系

根据式（7）和图1所显示的规律，对其中的影响因素结合桥梁安全事故进行分析，试图找到事故的规律性和控制途径。

施工系统的起始安全度和进入施工系统的人、设备以及外力等均有很大关系。人的安全度、环境的安全度、设备的安全度以及外来负作用力的影响等可以构成一个起始安全度，假设广义的各种因素起始安全度由不同的影响因子组成：人的因素物或设备因素环境的因素那么起始的系统安全度由不同的人、物、环境和负作用力因素决定，且随着时间变化，各种因子变化会造成安全度的变化。对于事故致因的分析，可以从几个方面进行，但目前由于事故数据的缺乏，很难找到各因素之间定量的权重关系、具体因子值。文章借鉴因果连锁理论对人和物的不安全状态的研究，研究发现事故原因中人的不安全行为占88%，物的不安全状态占10%，其他占2%。故假设人因的权重为0.88，物因的权重为0.1，环境因的权重为0.02%，则初始安全度表示为：DS0＝0.88 DSH＋0.1 DSM＋0.02 DSE。假设不同因素的起始安全度相同，依次变化为0.8、0.7、0.5，衰减系数为－0.5，时间步距划分为20份时，通过数学软件MATLAB处理得到不同起始安全度下的流变突变曲线，如图2所示。

图2 不同起始安全度下的流变突变曲线

从图2中可以看出，起始安全度对流变和突变速度没有影响，但对于流变突变拐点时间有影响，当施工系统中的人物环境起始状态安全度较高时，发生事故的时间会后移。从事故本质上讲，当外界作用力一定时人物环境自身的状态是影响事故的主要原因。

在DS0＝0.8时，假设衰减系数分别为－0.2、－0.4、－0.6、－0.8，观察流变突变曲线变化，如图3所示。

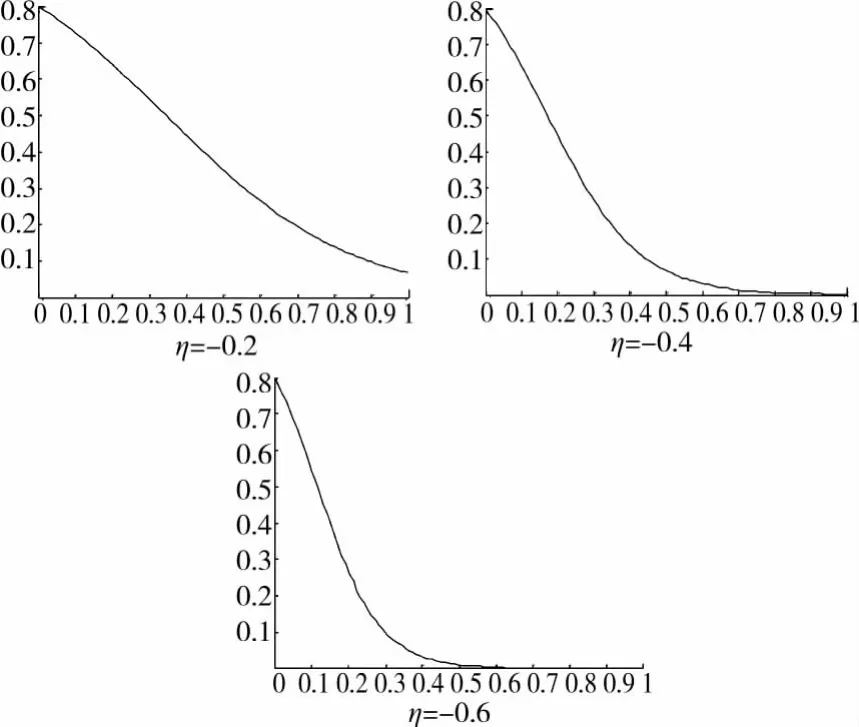
图3 不同衰减率的流变突变曲线

从图3衰减率对流变突变的影响看，当衰减率值增大时，流变速度增大，事故安全度随时间的加速度变大，流变突变拐点时间提前；当衰减率较低时，在预计的事故发生时间内可能不会出现事故，这是施工过程中期望的情况。

衰减率除了与影响初始安全度的这些因素有关，这些因素对安全度和流变曲线的贡献是提高曲线起始点，增大拐点时间。但对衰减率的作用恰好相反，因此可以假设衰减率与起始安全度成反比，从图3衰减率对流变影响和事故经验可知，还应有一个影响衰减率的因素，即外界负作用力影响因子当该作用力越大，衰减率越大，因此衰减率可以表示为这种外界负作用力既可以表现为具体的外力，也可以是人物环境的不利变化。

3.2 流变突变模型的假设性验证分析

通过几组假设的施工系统利用上面的分析说明事故致因，施工系统A：人员心理素质、技能等方面均具有较高水平，设备稳定可靠，环境适合作业，该施工过程中，人物环境对事故可能性的影响权重为0.5：0.2：0.3。施工过程中的负外力主要来自于自然环境的变化。

施工系统B：人无环境因素较A稍低，施工过程的影响权重和A相同，施工过程中负外力主要来自原自然环境变化，但较A更容易受到环境影响。

施工系统C：人物环境水平和A相当，但该施工过程中人物环境对事故可能性影响权重为0.5：0.4：0.1，施工中的负外力主要来自于设备所承担的荷载重量。

施工系统D：任务环境水平较A稍低，施工过程影响权重和C相同，施工中主要负外力来自于设备所承担荷载重量，但受荷载重量影响较C弱。

其主要影响因子如表3所示。

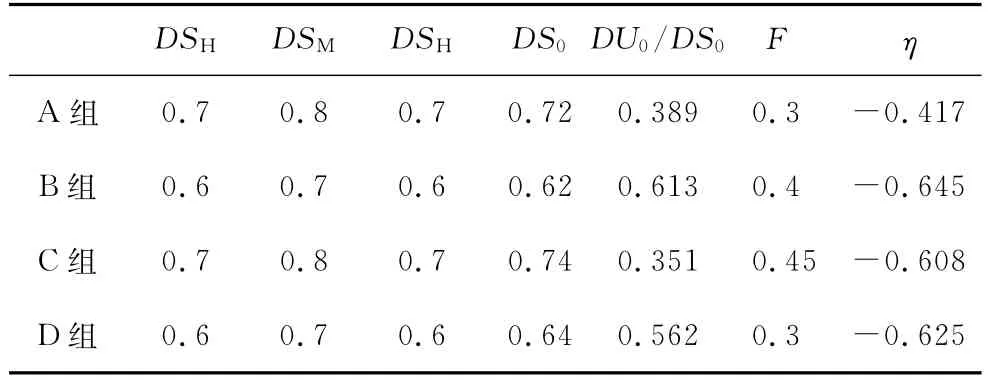
表3 事故流变突变分析假设参数表

利用软件进行流变突变函数的绘制，得到图4结果：

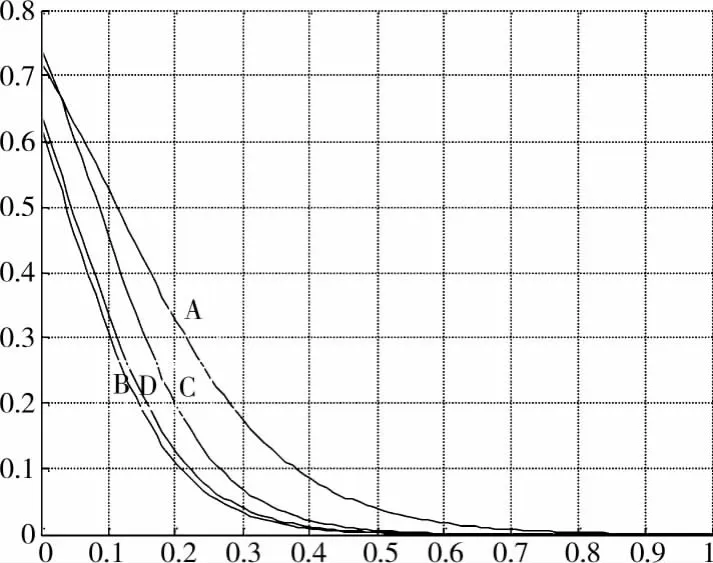
图4 不同假设因子的安全度衰减曲线

若假设负外力影响只对有影响的因素产生作用，那么衰减系数可以取为负外力因子和其影响因素安全度的比值，此时安全度衰减曲线如图5所示。

图5 负作用力对影响因素作用的衰减曲线

从图4可以看出，这种流变突变曲线非常吻合实际施工情况，即一旦事故进入发生过程，没有过多的流变阶段。施工系统C虽然起始状态较A安全，但由于负外力影响大，因此较A提前进行突变期，先发生事故。从表3的起始安全度来看，施工系统A和C，B和D虽然各因素起始安全状态相当，但由于在施工过程中所占权重不同，最终的系统状态起始安全度也有所不同。对于A组和D组，当外力影响因子相同时，由于起始状态不同，导致衰减系数不同。

从图5中可以看出，若负外力只对其影响因素发生作用时，施工系统C将比系统D更早发生事故，这种方法对于施工系统中某一因素受外力作用较敏感时较为适用。

从以上4组验证性假设可以看出，施工系统的安全事故发生是由组成系统的不同因素的状态和外界对这些因素的影响共同作用而成的，当系统在自身组成因素和外界负作用力作用下，会出现事故趋势，进而加速出现事故，直到事故结束。按照流变突变理论观点，事故的发生是不可避免的，因此对于施工安全事故应尽可能的延缓事故时间，从流变突变模型和曲线规律来看，主要是要保证进入施工系统的人机物环境的良好状态，提供一个较高的起始安全度。对于外力作用影响，则尽可能减少其对系统因素的影响。

4 常见桥梁安全事故的流变突变实证研究

从事故致因模型和流变突变曲线分析得到了事故致因的本质条件的进入施工系统的不同因素的安全度的衰减。由于在一般事故中较难获取各种因素随事故时间的变化情况，而且不同的施工系统的权重、负作用力均不同。桥梁施工过程中，支架坍塌是常见的安全事故，笔者通过对支架结构的施工期变形的监测数据和某次支架坍塌事故来验证流变突变模型。

4.1 数据处理及系统安全度计算

统计了某施工现场支架垮塌前所测得变形数据，采用转换和估算的方法进行支架坍塌事故的流变突变模型的研究，表4为一支架群施工项目的几个墩梁支架挠度测量变化值，其中测量时次为从立模绑扎钢筋到混凝土浇筑时中间的测量，测量间隔时间为4h，在2d时间内共进行9次测量。

对于支架施工和支架坍塌事故，系统的不安全度同样来源于人机环境以及负外力影响，但由于缺乏对人和环境的数据，因此这里支架变形量作为在负外力和人机环境下的总影响结果。实测支架群为30m跨支架，实际计算跨度为27m，可以得到其理论最大变形量为67.5mm。为保证2倍安全系数，这里取允许最大挠度为35mm。随着支架挠度增大，理论上安全事故可能性增大，因此令系统总安全度为实测变形量，fmin为允许安全挠度，利用这种方法进行确定后可以得到几个支架体系的安全度随测量时间的变化如表4所示。

4.2 支架坍塌事故流变突变规律拟合

多个系统分析时，如果不容易确定总时间T和步距划分，可以按照式（5）进行分析，用数学模型MATLAB对表4中的数据进行拟合可以得到各支架的流变突变模型如表5所示。

表4 以变形量为度量的支架系统安全度

表5 拟合的支架安全度衰减规律

各支架安全度衰减规律图6所示。

从图6可以看出，各支架安全度遵循流变突变特征，且支架B的事故时间最短。

4.3 坍塌事故分析

在该支架群施工中，支架A、C、D、E顺利完成了施工任务，并及时拆除。而支架B在底腹板浇筑完后出现了垮塌，如图7所示。

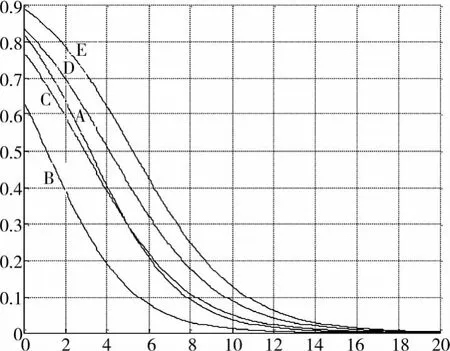
图6 支架安全度衰减规律

图7 支架B垮塌现场图

从流变突变规律看，最终系统都将进入崩溃，但对于出事支架是其事故时间较支架服役时间短，因此发生事故，而其他结构的事故时间点上临时结构已退出使用，进入下一个施工系统中。从安全度衰减规律分析这次事故，施工系统的起始安全度太低，按照前述的人机环境原因分析为：由于施工人员支架设计理解错误，将30对双排双层贝雷片设计施工成为30片，因此对于施工结构系统本身已经是一个具有极大风险度的系统，在浇筑过程中没有及时发现支架的异常变化，当底板和腹板浇筑完成后支架安全度在重量和施工荷载的负作用影响下安全度下降迅速，最终出现事故。