新型复合竹层积材的顺纹销槽承压强度计算公式

李霞镇，钟 永，2，任海青，2

（1.中国林业科学研究院 木工所，北京100091；2.国家林业局 木材科学与技术重点实验室，北京100091）

中国竹资源拥有量和品质均居世界首位，竹子具有生长速度快、成材早和产量高等特性，属于短期的可再生资源［1］。随着新型复合竹质工程材料技术的突破，将改变中国竹质材料大多被应用于地板和集装箱等非建筑结构应用领域的现状，为其在建筑结构领域奠定基础。

在现代木结构设计中，销槽承压强度是销连接设计的基础参数之一，被列入各国木结构设计规范中［2－4］。国外学者Kweonhwan［5］、Douglas［6］、Kei［7］、Wataru［8］、Chui－Ki［9］、Marc［10］、M.A.［11］、Alfredo［12］等，研究了木材密度、销径、端距、含水率、纹理方向等因素对规格材、胶合木等工程木销槽承压力学性能影响，得到了销槽承压强度理论计算公式。黄绍胤［13－14］、樊承谋［15］、王振家［16］最早研究了 销径、孔 径和进钻速度等因素对销槽承压强度的影响，得到了圆钢销连接承弯、承压的可靠度指标。刘柯珍［17］研究了销径、厚度、纹理方向等对胶合木销槽承压的力学性能影响。但作为新型复合竹质材料的销槽承压力学性能，尚未有相关研究。

为研究该新型复合竹层积材顺纹销槽承压的力学性能，课题组参照木结构试验方法［18］，进行了7组，共28个销槽承压试件测试，分析了竹层积材厚度、销直径和端距对其力学性能的影响，建立了其承压强度的计算公式，将为其在建筑结构中的设计与应用提供初步参考。

1 试验概况

1.1 销槽试件制造

针对竹层积材顺纹销槽承压的影响因素，共设计了7个测试组，其中竹层积材厚度T、销直径D、端距S变化各3组，ZT－3测试组又兼为ZS－3和ZD－3，每组含4个试样，测试组的具体参数见表1。

表1 测试组的基本参数

竹层积材销槽承压试件见图1，X为顺纹方向，即竹层积材的长度方向；Y为径向，即厚度方向；Zv为弦向，即宽度方向。其中，竹层积材销开半圆孔，孔直径比销直径大1mm。销的材料为 Q235，等级为4.8级［2］。

图1 销槽承压试件示意图

1.2 试验用竹层积材

试验用竹层积材为典型的正交各向异性材料，为四川竹元科技公司制造的新型高性能竹基复合材料，材种为丛生竹，其加工过程为：竹材→剖分→疏解→胶前干燥→浸胶→胶后干燥→装模→热压固化→脱模→竹层积材。

采用10tInstron5582万能力学试验机测试竹层积材的物理力学性能［19］。测得其含水率约为4%，密度为1.1～1.3g／cm3。表2为各方向的强度平均值及其变异系数。

表2 竹层积材材性

1.3 试验加载及量测

图2为试验加载装置图。采用30t万能力学试验机对竹层积材销槽承压试件进行测试，加载速度为1mm／min［18］。当钢销完全嵌入竹层积材试件或载荷出现明显下降时，停止加载。

图2 试验加载装置

2 试验结果分析

2.1 破坏现象

竹层积材顺纹销槽承压时，各测试组的破坏形式均相同，见图3。

图3 销槽承压的破坏模式

钢销的弹性模量、强度均远高于竹层积材，因此可假设销为刚体，即销在整个加载过程中不发生变形。竹层积材在加载初期处于弹性阶段。随着载荷增加，竹层积材的销开孔两端受局部挤压变形并出现细微裂纹。持续加载，裂纹沿竹层积材表面扩展，并逐渐向里延伸，直至裂纹贯穿整个竹层积材，载荷出现明显下降，停止加载。

2.2 荷载-位移曲线

图4为竹层积材顺纹销槽承压各测试组的荷载-位移曲线，其曲线形式基本一致，呈脆性破坏。曲线在加载初期呈非线性，主要原因是加工精度误差导致销与竹层积材间存在初始空隙。随着载荷增加，初始空隙消除，竹层积材处于线弹性阶段，曲线进入线性阶段。

持续加载，竹层积材的销开孔两端因应力集中的影响［20］，局部产生塑性变形并出现细微裂纹，此时竹层积材仍能继续承载。但因细微裂纹的快速扩展导致整个竹层积材被裂纹贯通，销槽散失承载力，曲线进入破坏阶段。

但文献［17］中胶合木顺纹销槽承压测试的塑性变形阶段较明显，并未发生脆性破坏，与文中采用竹层积材测试的结果不一致。从上述测试的竹层积材顺纹承压荷载-位移曲线（图5）可知，有明显的塑性变形阶段。结合图3～5及实验现象，可判断竹层积材顺纹销槽承压呈脆性破坏，主要是因为竹层积材用胶为脆性材料，当局部应力达到胶粘强度时，竹层积材表面出现细纹裂纹且产生局部塑性变形，但随着裂纹快速贯通整个竹层积材，载荷出现明显下降，竹层积材大部分销槽承压截面并未达到顺纹承压强度。

2.3 刚度、最大载荷、承压强度

从图4中分析可知，竹层积材顺纹销槽承压时，基本无塑性变形阶段，文中取最大载荷值Fmax计算销槽承压强度，对应的位移作为最大位移值［21］。其承压强度计算公式如下：

式中：fe为销槽承压强度，MPa；Fmax为销槽承压的最大载荷，kN；D为销直径，mm；T为竹层积材厚度，mm。

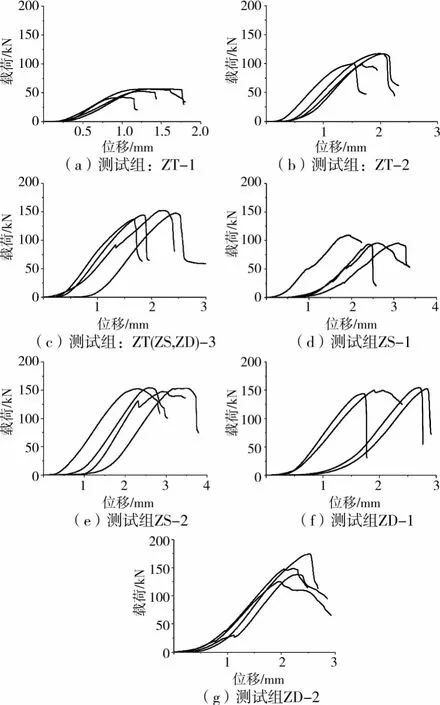
图4 试件荷载-位移曲线

图5 竹层积材顺纹方向抗压荷载-位移曲线

竹层积材销槽承压各测试组的力学性能参数统计的平均值见表3。

表3 销槽承压计算结果

续表3

由于竹层积材为工程复合材料，避免了竹节、空洞和腐朽等天然缺陷所导致的力学性能差异［21］，且与规格材、结构胶合木等木质材料相比，其密度的变异系数可忽略不计，因此各测试组试样的力学性能参数均较稳定。

3 影响因素分析

3.1 竹层积材厚度

比较竹层材厚度（测试组ZT－1、2、3）对销槽承压的刚度K、最大载荷Fmax和承压强度fe等力学性能的影响，见图6。

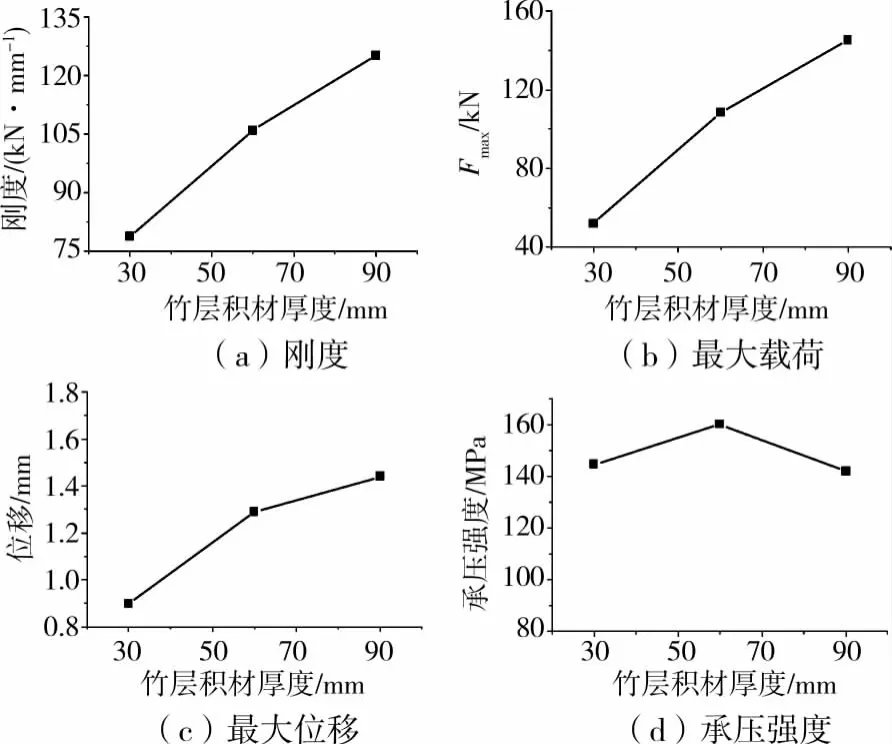
图6 竹层积材厚度T对销槽承压性能的影响

从图6可知，随着竹层积材厚度的增加，销槽承压的刚度、最大载荷和最大位移均大致呈线性增长，增幅分别为0.772（kN／mm）／mm、1.557kN／mm、0.009 2mm／mm。而承压强度值则随厚度的增加，基本保持不变，主要是因为销槽承压截面沿厚度的应力不均匀分布现象［20］，在局部塑性变形后可发生内应力重新分布，与文献［13－16］结果相同。

3.2 端距

比较端距（测试组ZS－1、2、3）对销槽承压的刚度K、最大载荷Fmax和承压强度fe等力学性能的影响，见图7。

从图7可知，随着端距的增加，销槽承压的刚度、最大载荷均先增加后基本保持不变。而最大位移则随厚度增加，基本保持不变。对于承压强度，当端距为48mm时，其承压强度明显小于其它测试组；当端距大于64mm，其承压强度基本保持不变。从木结构设计规范可知［2－4］，端距在满足一定几何构造要求后，可避免销槽发生撕裂破坏。对于该新型复合竹层积材，则要求端距不应小于64mm。

3.3 销直径

比较销直径（测试组ZD－1、2、3）对销槽承压的刚度K、最大载荷Fmax和承压强度fe等力学性能的影响，见图8。

图7 端距S对销槽承压性能的影响

图8 销直径D对销槽承压性能的影响

从图8中可知，随着销直径的增加，销槽承压的刚度、承压强度和最大位移基本保持不变，而承压强度则呈线性递减，与文献［2－4］结果一致。

4 顺纹销槽承压强度计算公式

销槽承压强度为销连接设计的基础参数之一。由于缺乏试验基础数据，中国现有木结构设计规范中规定销槽承压的强度取值为木材的顺纹承压强度［2］。而加拿大、美国木结构设计规范则采用木材相对密度G和销直径D作为基础参数进行计算，如下：

加拿大设计公式［3］：

美国设计公式［4］：

因木材密度与其顺纹承压强度之间基本呈线性［21］，式2、3中的密度用木材顺纹承压强度代替后，与中国木结构设计规范销槽承压强度取值方法相同。

通过上述竹层积材顺纹销槽承压力学性能的影响因素分析（图6～8），表明其承压强度主要受销直径D的影响。基于此及文献［2－4］，建立了竹层积材顺纹销槽承压强度的理论计算公式：

式中：KD为销直径的影响系数；fc，0为竹层积材顺纹抗压强度161.46MPa，a0为待确定系数。

以测试组ZD－3（T＝90mm、D＝12mm、S＝64mm）作为基准组，其KD取值为1.0，则系数值a0等于其销槽承压强度与竹层积材顺纹抗压强度的比值fe／fc，0，即0.88。由图8（d）知销直径与承压强度大致成线性递减，因此对测试组ZD－1、2、3，以D／12为横坐标，以各测试组相对于基准组的承压强度比值为纵坐标，采用线性回归拟合，如图9所示。

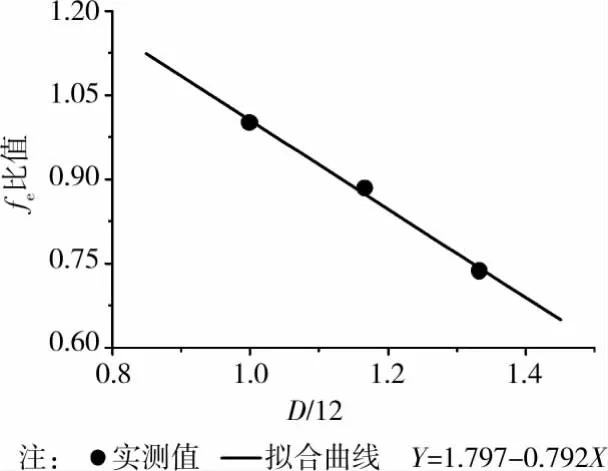
图9 销直径影响系数KD的拟合结果

从图9中的拟合回归分析结果，表明竹层积材顺纹销槽承压中的销直径影响系数KD可采用公式5计算：

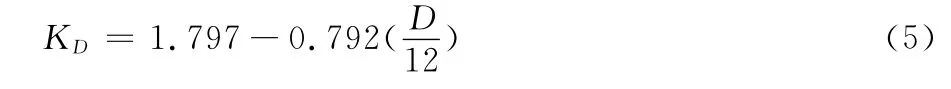
采用以上影响系数代入式fe＝0.88 KDfc，0计算各测试组的销槽承压强度，并与实测值比较见表4（不包含测试组ZS－1），表明该理论计算公式能够准确预测竹层积材顺纹销槽承压强度值。

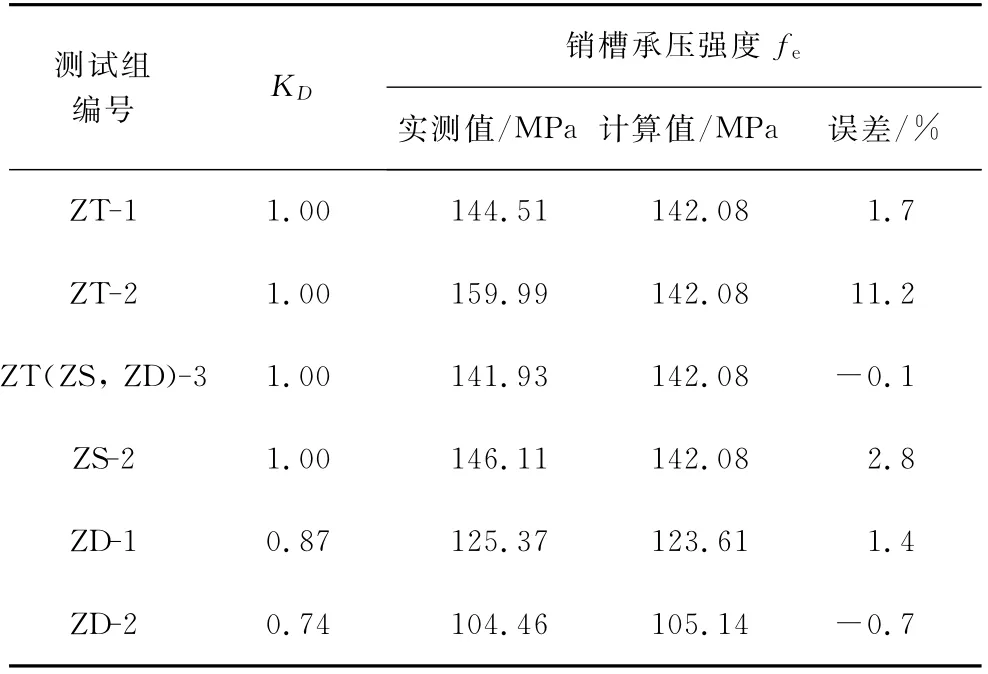
表4 销槽承压计算结果比较

5 结 论

通过7组共28个复合竹层积材顺纹销槽承压试件的试验研究，获得如下结论。

1）竹层积材顺纹销槽承压破坏形式呈脆性破坏。

2）竹层积材顺纹销槽承压强度主要受销直径D的影响，而受竹层积材厚度的影响较小。当其端距不小于64mm时，端距对销槽承压强度的影响可忽略不计。

［1］刘一星，赵广杰.木质资源材料学［M］.北京，中国林业出版社，2004.

［2］GB／T 5005－2003木结构设计规范［S］.中国建筑工业出版社.北京：2009.

［3］Canadian Standard Association International，CSA Standard.O86－09.Engineering design in wood ［S］.Ottawa，ON，Canada，2009.

［4］American Forest ＆Paper Association，American Wood Council.NDS－2005National design specification for wood construction［S］.Washington DC，2005.

［5］Kweonhwan Hwang and Kohei Komatsu.Bearing properties of engineered wood products I：effects of dowel diameter and loading direction［J］.Journal of Wood Science，2002，48：295－301.

［6］Rammer D R，Steve G.Winistorfer.Effect of moisture content on cowel－bearing strength［J］.Wood and Fiber Science，2001，33（1）：126－139.

［7］Sawata K，Yasumura M.Determination of embedding strength of wood for dowel－type fasteners［J］.Journal of Wood Science，2002：48：138－146.

［8］Kambe W，Itgaki N，Iijima Y.A Study of bearing strength with different end－distance，bolt－diameter and wood species ［C］／／11th World Conference on Timber Engineering.Riva del Garda：WCTE，2010：384.

［9］Kin C K，Oh J K，Lee J J.Effect of moisture content on performance of dowel－type connection ［C］／／ 11th World Conference on Timber Engineering.Riva del Garda：WCTE，2010：439.

［10］Oudjene M，Khelifa M.Experimental and numerical analyses of single double shear dowel－type timber joints［C］／／11th World Conference on Timber Engineering.Riva del Garda：WCTE，2010：796.

［11］Zitto M A S，Köhler J C，Piter J C.Embedding strength in joints of fast－growing Argentinean Eucalyptus grandis with dowel－type fasteners.Analysis according to the criterion adopted by European standards［J］.European Journal of Wood and Wood Products，2012，70（4）：433－440.

［12］Pereira A M，Willem J，Maria H，et al.Numerical modeling of the load－deformation behavior of doweled softwood and hardwood joints ［J］.European Journal of Wood and Wood Products，2010：42（4）：480－489.

［13］黄绍胤，洪敬源，余培明.木结构螺栓连接中销槽木材承压和钢销抗弯的强度［J］.重庆建筑工程学院学报，1986（1）：11－17.Huang S Y，Hong J Y，Yu P M.Bearing and bending strength of pin connections in timber structure［J］：Journal Chongqing Institute of Architecture and Engineering，1986（1）：11－17.

［14］黄绍胤，余培明，洪敬源.木结构中螺栓连接的设计承载力及其可靠度［J］.四川建筑科学研究，1986，（3）：1－5.Huang S Y，Yu P M，Hong J Y.Reliability and strength of bolted－connection design of timber structure ［J］：Building Science Research of Sichuan，1986（3）：1－5.

［15］樊承谋.木结构螺栓联接的工作原理及计算公式：关于国际木结构设计规范第五稿螺栓联接计算公式的讨论［J］.哈尔滨建筑工程学院学报，1982（1）：18－36.Fan C M.The Bolted－connection design of timber structure：discuss about the bolted－connection design for International design of timber structure［J］：Journal of Harbin University of Civil Engineering and Architecture，1982（1）：18－36.

［16］王振家.圆钢销连接承弯、承压承载能力可靠度分析［J］.哈尔滨建筑工程学院学报，1984（4）：32－45.Wang Z J.Reliability analysis of bending and bearing strength of pin connection ［J］.Journal of Harbin University of Civil Engineering and Architecture，1984（4）：32－45.

［17］刘柯珍.落叶松胶合木梁柱连接节点设计与承载性能评价［D］.北京：中国林业科学研究院，2011.

［18］GB／T 50329木结构试验方法标准［S］.中国建筑工业出版社.北京：2002.

［19］GB／T 1928－2009木材物理力学试验方法总则［S］.北京：中国国家质量监督检验检疫总局，2009.

［20］Moses D M，Prion H G L.A three－dimensional model for bolted connections in wood［J］.Canadian Journal of Civil Engineering，2003（30）：555－567.

［21］潘景龙，祝恩淳.木结构设计原理［M］.北京：中国建筑工业出版社，2009.