混合断路器中串联功率二极管反向恢复暂态过程研究

鲁 洪，彭振东

（武汉船用电力推进装置研究所，武汉 430064）

0 引言

混合式断路器是近年来国内外研究的一项热门课题，从最初基于两级换流思想构成的零电压开关、零电流开关，发展到现在基于三级换流思想构成的零电压零电流混合式断路器，其基本原理都是先将电流从机械开关转移至由半导体开关组成的换流回路，然后依靠半导体开关完成电流的分断[1,2]。从而兼具机械开关良好的静态特性和半导体器件无弧、快速分断的动态特性，在一定程度上弥补了传统机械断路器的不足，是未来电力系统保护设备的发展方向。

图1 P-I-N功率二极管

除了零电流开关之外，其余混合式断路器均要依靠机械开关开断时产生的电弧电压迫使电流向换流回路转移，由于电弧电压较小，从电路理论可知，要想实现电流的迅速转移，必须尽量减小半导体器件的通态压降[3,4]。从已有的文献来看，基本上都是基于 4层（PNPN）结构的晶闸管、GTO、IGCT或IGBT来实现的[1-4]，与P-I-N功率二极管（图 1（a））相比，这类器件的通态压降比较大，因此笔者正在从事基于功率二极管的三级换流混合式断路器课题研究。为了提高装置的电压等级，混合式断路器中采用了串联二极管组件，但是在试验研究过程中，经常出现二极管失效的情况，究其原因，是因为串联二极管的均压措施未曾处理得当所致。尽管关于半导体器件的串联均压技术研究已经有过许多报道，但是鲜有直接涉及到二极管的，基本都按晶闸管的串联分析方法进行处理[5]。在混合式断路器这种特殊的应用场合，二极管的暂态峰值电流和关断电流下降率极大，由此引起的二极管反向恢复过程更加严重，对吸收保护电路提出了更高的要求。因此有必要对串联二极管的反向恢复暂态过程进行详细的分析，研究其差异性对串联电压分布的影响，为二极管组件的优化设计提供理论依据。

1 二极管的反向恢复模型

二极管的微观电荷运动理论表明，由于正向导通期间的大电流注入效应，使N-区积累了大量的少数载流子，在二极管关断过程中，这些过剩的载流子无法立即消失，需要通过迁移、扩散、复合等方式逐渐降低浓度[6]。受外电路电感的影响，二极管无法在电流过零时关断，而是随着反向电流对过剩载流子的逐步清除才能逐渐恢复阻断状态。在这个过程中，反向电流会首先上升到一个峰值 IRM，然后迅速减小到反向饱和值，如图1（b）所示。

目前二极管模型主要有：功能模型、物理模型和集总电荷模型。功能模型只考虑器件的外部特性，不考虑器件内部复杂的物理过程，仿真速度快，但是精度不够；物理模型虽然精度很高，然而需要的参数太多，并且计算速度很慢；集总电荷模型将物理模型进行了适当的简化，参数提取容易，且精度较高，工程应用价值较大。

集总电荷的概念是将电荷存储区分为几个部分，过量的存储电荷被集中置于每个存储部分中间的一个节点中。根据载流子的微观运动理论，可得完整的二极管模型如下[7]：

其中，qM为 N-区存储电荷，qE为结边界存储电荷，TM为运输时间，τ为载流子寿命，i为二极管电流，Is为二极管反向饱和电流，v为二极管结电压，VT=KT/q为温度电压当量，k为玻尔兹曼常数，T为PN结绝对温度。

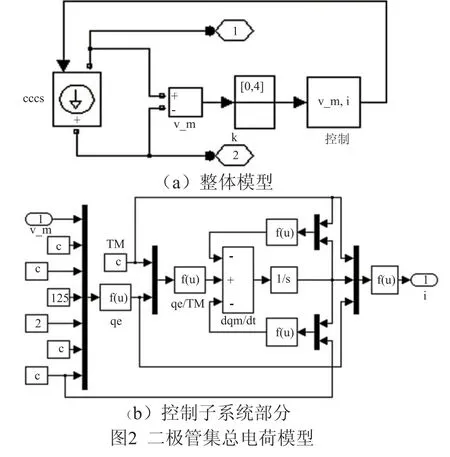
由此在 MatlabSimulink中实现的集总电荷模型如图2所示，模型以可控电流源为核心部件，通过电压传感器采集电流源两端的实时电压并传给控制子系统，控制子系统接收模型参数和实时电压值，按照式（1）、（2）、（3）进行计算，得到二极管的实时电流值，将该电流值作为可控电流源的控制输入信号[8]。

2 串联二极管的反向恢复过程

混合断路器中的串联二极管组件实际工作电路及等效电路如图 3所示，其中 R1=R2=R3和C1=C2=C3分别为二极管D1、D2的吸收电阻和吸收电容，L为电路等效电感， C为预先充电电容，S为合闸开关，ir1(t)和ir2(t)分别为D1、D2反向恢复过程中的等效电流源，i(t)为回路电流，U为反向恢复时刻电容C上的电压瞬时值。为了简化分析，假定反向恢复电荷Qrr1＜Qrr1，反向峰值电流时刻t1＜t2，D1、D2反向恢复电流各自按指数规律变化，即

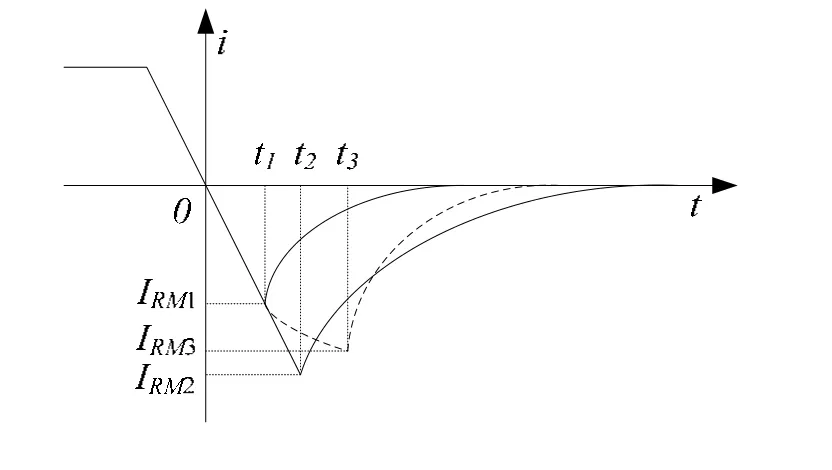
图4 串联二极管的电流示意波形

那么在 t1时刻之前，二极管 D1、D2电流均以相同的电流变化率 di/dt=U/L反向增加，两二极管均维持在低通状态；在 t1时刻， D1到达反向恢复电流峰值 IRM1；此后在 t1～t3期间，D1开始恢复反向阻断能力，电流ir1(t)开始反向减小，但由于D2仍然处于低通状态，因此反向电流ir2(t)- ir1(t)将会向C1充电，D1两端电压u1(t)开始反向增加，在此瞬态过程中电容电压基本为恒定值U，则D2电流将以变化率

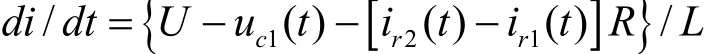
到达峰值IRM3[9]；在t3时刻之后，二极管D1、D2均处于反向阻断能力恢复阶段，吸收回路中R1、C1、R2、C2将同时作用，抑制二极管两端的电压变化率，吸收电感L中的瞬时能量。此过程各电流的示意波形如图4所示。

若取如图3（b）所示的参考方向，那么（1）t＜t1时

两只二极管均未开始恢复阻断特性，维持在低通状态。

（2）t1≤t＜t2时

（3）t≥t2时

因此先根据式（6）、（7）求得电流 i(t)后，再由式（8）即可求得恢复阻断时二极管两端电压u1(t)和u2(t)，然后由式（9）计算电压差Δu(t)。当二极管 D1、D2完全恢复阻断能力后，反向电流近似为零，则电阻上电压为零，电压u1(t)和u2(t)中只有电容电压分量。由此可得串联两只二极管完全阻断时的电压差为

3 仿真计算验证

利用课题研究中的试验参数对上述串联二极管的反向恢复暂态过程及其相关理论分析进行了验证，利用Simulink中建立的集总电荷模型对串联二极管的反向恢复暂态过程进行了仿真。计算和仿真参数如表1所示，计算和仿真结果如表2和图5所示，其中Δt为两只二极管进入反向恢复阻断过程的时间差，UP1和 UP2分别为反向恢复过程中两二极管的反向电压峰值。

从计算和仿真结果可以看出，由于计算时采动态物理变化过程，并将两只二极管假设为两个单独的等效电流源，没有考虑串联工作时两只二极管之间的相互影响，因此与基于能较为准确反映二极管内部载流子运动过程的集总电荷模型仿真结果相比，计算结果存在些许误差，但是误差均能控制在3%以内。

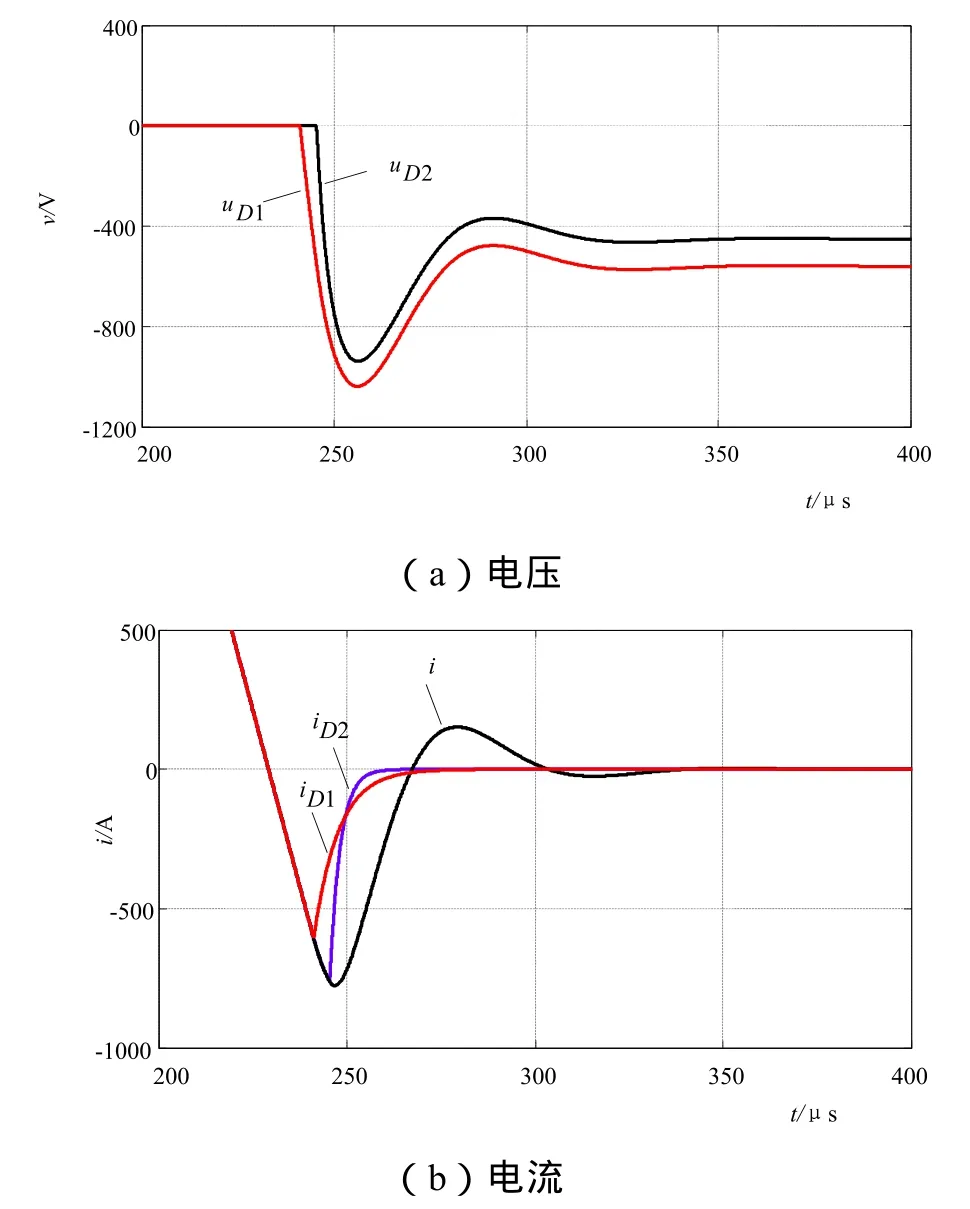
图5 串联二极管仿真电压电流波形

4 结论

在串联二极管的关断过程中，二极管反向恢复电荷的差异性是导致在反向恢复暂态过程以及恢复阻断后出现电压不均的根本原因，稳态阻断后的电压差近似等于恢复电荷差值ΔQrr与吸收电容Cs的比值，而峰值电压差一般较稳态电压差略小。

因此为了减小串联二极管关断时的电压差，用了较为简单的指数恢复模型，忽略了二极管的应尽量挑选恢复电荷 Qrr一致的器件进行串联，并适当增加吸收电容Cs的容值。

另外，数值计算结果与基于MatlabSimulink实现的二极管集总电荷模型仿真结果保持一致，验证了文中反向恢复暂态分析方法的合理性和有效性。

:

[1]B. Roodenburg, A. Taffone, E. Gilardi,et al. Combined ZVS-ZCS topology for high-current direct current hybrid switches: Design aspects and first measurements[J]. IET Electronic Power Applications,2007, 1(2):183-192.

[2]王晨，张晓峰，庄劲武等.新型混合式限流断路器设计及其可靠性分析[J].电力系统自动化，2008，32(12)：61-66.

[3]Polman H, Ferreira J A.Kaanders M, et a1. Design of a bi-directional 600 V/6 kA ZVS hybrid DC switch using IGBTs[J]. IEEE Trans on Power Delivery, 2001,16(2):1052-1059.

[4]Jean-Marc Meyer, Alfred Rufer. A DC hybrid circuit breaker with ultra-fast contact opening and integrated gate-commutated thyristors [J]. IEEE Transactions on Power Delivery, 2006, 21(2):646-651.

[5]Jurg W, Bjorn B. Design of RC snubbers for phase control.www:library.abb.com/GLOBAL/SCOT/scot25 6.nsf/VerityDisplay/0040489C5516CD86C1256B9900 45BDCF/$File/prodinfo.pdf.

[6]维捷斯拉夫.本达.功率半导体器件—理论及应用[M].北京：化学工业出版社，2004.

[7]Ma C L,Lauritizen P O. A simple power diode model with forward and reverse recovery[J]. IEEE Trans On Power Electron, 1993, 8(4):342—346.

[8]彭振东，任志刚，王华敏. 固态断路器中快恢复二极管的反向恢复模型[J].船电技术，2012，32(3)：55-57.

[9]蓝元良，汤广福，印永华等.串联晶闸管反向恢复暂态过程的研究[J].电网技术，2006，30（16）：16-19.