用于分布式发电的六相永磁同步电机仿真建模
2013-08-10王舰威张凯
王舰威, 张凯
(1. 武汉船舶通信研究所, 武汉430205;2. 华中科技大学, 武汉 4300074)
0 引言
连接电力电子变流器运行时,多相(特指相数大于3)电机与同等容量的常规三相电机相比,由于具有每相电流定额低,转矩、电流脉动小,直流侧电压纹波小,故障容错性高等优点[1,4],在分布式发电等场合获得了日益广泛的应用。
本文将要讨论的是一台六相永磁同步电机。该电机转子为凸极,定子具有两套互差 30°且相互绝缘的三相绕组,如图1所示。该电机输出连接整流器,是一个分布式微型燃气轮机(Microturbine)发电系统(参见图2)的组成部分。图2中的不控整流器亦可换成PWM整流器,这样就可以实现机组自起动以及补偿发电机电枢反应等更高级的功能。为在Matlab/Simulink环境下对以上系统进行电路级仿真研究(以便选择合适的控制策略),需首先建立能与 Simulink提供的各种整流器仿真模块“电气互联”同步电机仿真模型。
本文首先推导建立了该电机在静止d1-q1-d2-q2坐标系下的数学模型,含电压、磁链、转矩、运动方程。在Matlab/Simulink仿真环境下,基于以上方程定义了一个描述电机内部机电动力学特性的S函数。为了实现与六相变流器模型的直接“电气连接”,将该电机视为“黑箱”,采用Simulink提供的电压检测、受控电流源等基本电路仿真模块搭建了S函数的外围电气接口。以上这种将电机模型以电路仿真模型的形式给出的做法,非常有利于将电机模型用于电路级仿真。而且与文献[5]针对“三相电机—变流器系统”提出的“受控电压源—可变阻抗”(Voltage Behind Reactance)方法相比,本文方法形式更简单,因而更适合六相电机场合。
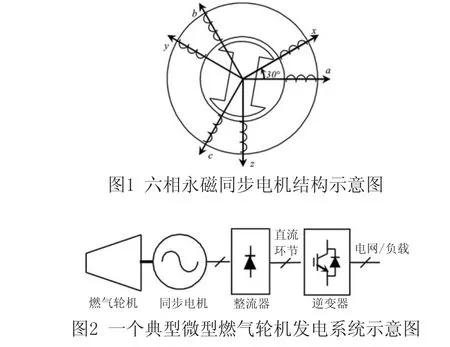
1 六相永磁同步电机数学模型
在原始六相(a-b-c-x-y-z)参考系下,定子电压方程为:

其中:
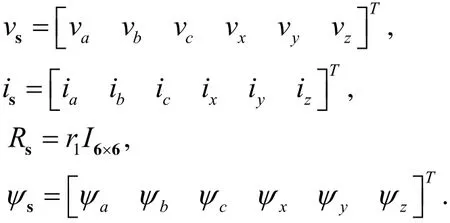
磁链方程为:

考虑到转子凸极效应,上式中的定子电感矩阵Lss可以表示为以下形式:
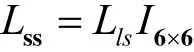
以上公式形式非常复杂,可采用坐标变换的方法加以简化。具体而言,将三相abc绕组变换到两相静止d1q1绕组、xyz绕组变换到d2q2绕组,d1-q1-d2-q2坐标系的定义如图3所示。
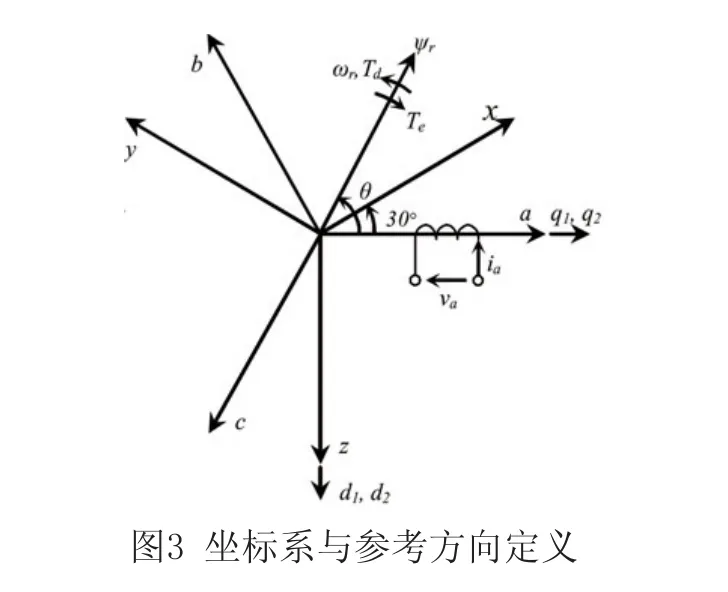
由于两套三相绕组均无中线,可推导出以下坐标变换关系,可整理成以下状态方程标准形式:
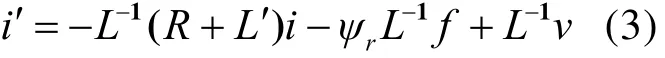
电机的机械运动方程为:
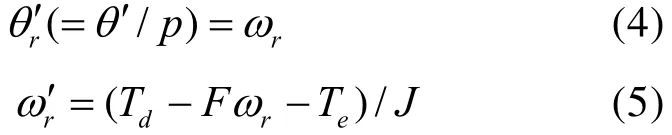
其中,θr, ωr, p, F, J 分别为转子机械位置角,机械转速,极对数,转子轴粘性摩擦系数,以及转子轴转动惯量。Td与 Te分别为来自原动机的驱动转矩和电机的电磁转矩。根据一般化电机基本理论可直接写出后者的表达式为:
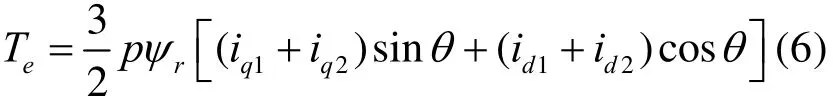
如希望得到形式更简洁、更便于理解的数学模型形式,可将以上两相静止坐标系进一步变换到两相同步旋转坐标系,但这需要更繁琐的推导过程。
2 仿真模型搭建
在Matlab/Simulink仿真环境下,可定义一个反映电机内部机电动力学特性的S函数。该S函数可视为该电机的状态方程描述,它以定子电压和外部驱动转矩为输入量;以电子电流、转子位置角、转子转速同时作为状态变量和输出变量,如表1所示。将定子电压处理为为输入量的原因是电机可能联结PWM整流器运行,此时电机端电压将由后者的开关状态决定。
Matlab/Simulink已提供了很多基本的电路仿真模块,如二极管整流器、PWM 整流器等。为了建立描述电机在虚拟坐标系下状态方程的S函数模块与以上变流器模块的“电气”互连,需要为前者搭建一个与实际电机6个接线端相对应的对外电气端口。

表1 同步电机 S函数变量表列
文献[5]在研究“三相同步电机—变流器系统”电路仿真模型时,为解决此问题,采用了电机在原始坐标系下的数学模型,并将其变换成适合用受控电压源、可变阻抗等电路仿真元件来描述的形式,由此给出电路图形式的电机模型,以便与变流器电路模型相连接。由于本文针对六相电机,以上方法就显得过于麻烦。
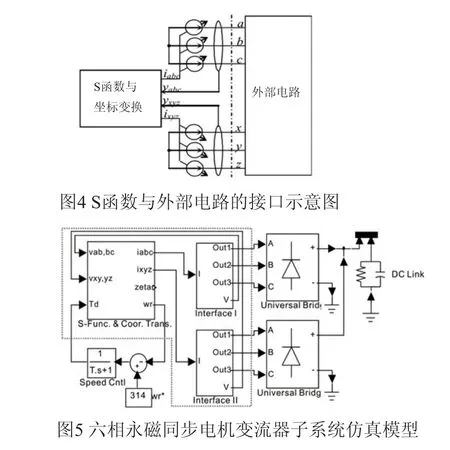
本文借助Matlab/Simulink提供的便利条件,采用了一种更简单的方法,即:利用电压检测模块将电气接口上的“物理”电压转化为数值信号,经坐标变换后,与来自原动机的驱动转矩信号一起作为S函数的输入;后者计算出d1-q1-d2-q2坐标系下的定子电流后,经坐标反变换得到六相实际电流值,最后通过受控电流源将与计算值相符的电流耦合到电气接口。图4是电气接口的一个简要示意图。这样一来,对于外接变流器而言,同步电机就等效为两组三相受控电流源,其输出电流大小则由端口电压以及原动机驱动转矩联合决定。
值得注意的是,以上方法仅保证在“电气接口”上忠实地反应电机的电气特性,并不保证受控源的中点电位也能严格对应实际电机绕组的中点电位。因此,以上提到的“端口电压检测”必须严格限制在电气接口上进行。换言之,只能检测线电压。如检测相电压则可能得到与实际不符的结果。原始坐标系下的线电压与 d1-q1-d2-q2坐标系下电压之间的坐标变换关系是:
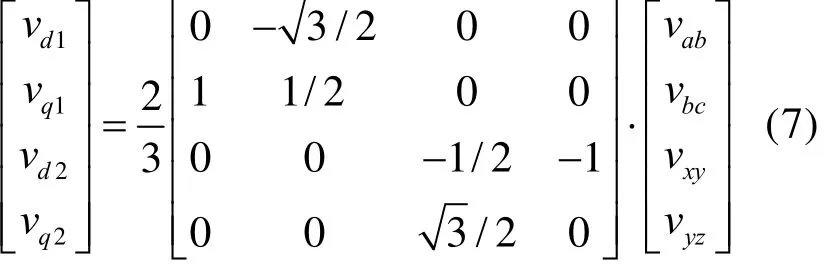
3 模型验证
六相永磁同步电机——变流器子系统Matlab/Simulink仿真模型最终形式如图5所示。其中虚线框内为同步电机部分的模型,由S函数及配套坐标变换/反变换模块以及两个三相电气接口模块组成,详情如上文所述。同步电机输出接 12相二极管整流器,后者直接取自 Simulink仿真模型库。视情况需要,直流环节后还可方便地接入电网侧PWM逆变器模型。或者亦可将不控整流器换成功率可回馈的PWM整流器,以实现原动机的冷启动,以及通过控制电机无功而改善其电压调整率等更高级的控制功能。
图5中的原动机即燃气轮机的转速调节机构不是本研究的重点,因而作了简化处理。转速调节器以及描述原动机转速响应特性的数学模型,以一个带限幅的一阶惯性环节一并表示。
采用如表2所示的参数值(LB 取负值是因为该凸极永磁同步电机的直轴电抗小于交轴电抗),图6是电机在燃气轮机拖动下的起动过程中,转子转速、直流环节电压、整流器输出电流、定子电流的仿真波形。为观察方便起见,图中最下端单独给出了a相定子电流波形。
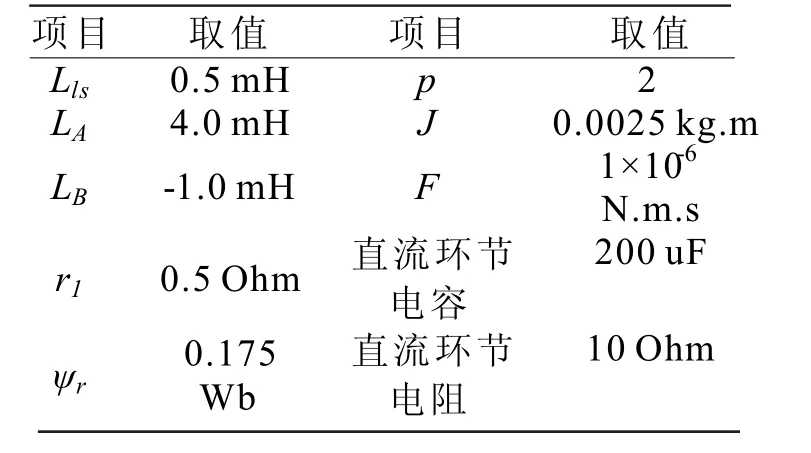
表2 仿真参数
由于暂不具备实际电机实验条件,故采用一种间接手段对以上所建仿真模型的正确性进行了验证。具体思路是:将以上六相电机的任一套定子三相绕组开路,则该电机的运行特性应该完全等同为一台三相电机。将以上工况下的仿真结果与Simulink模型库中提供的标准三相凸极永磁同步电机仿真模块的仿真结果对照,如二者完全一致,则可以确定所建模型的正确性。
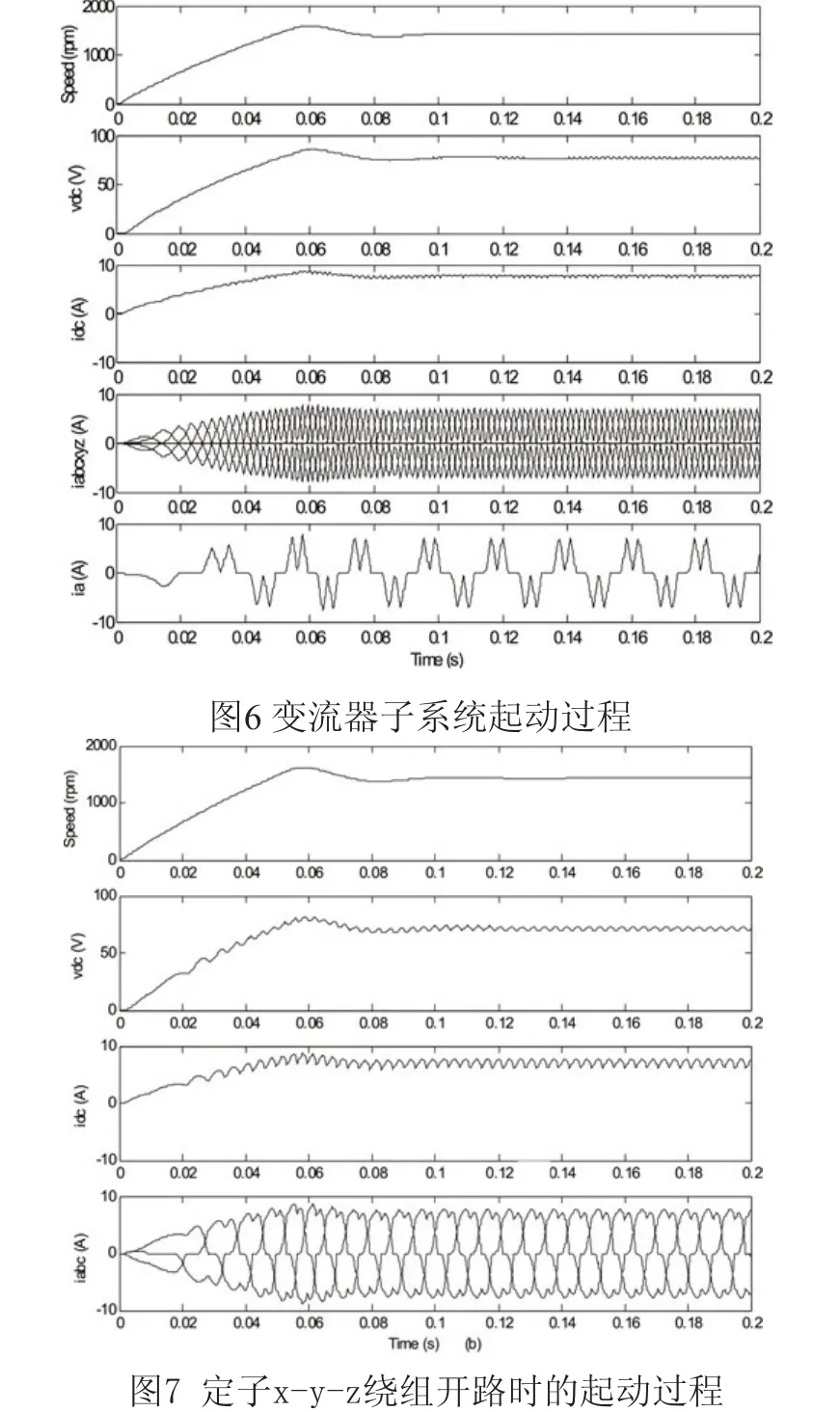
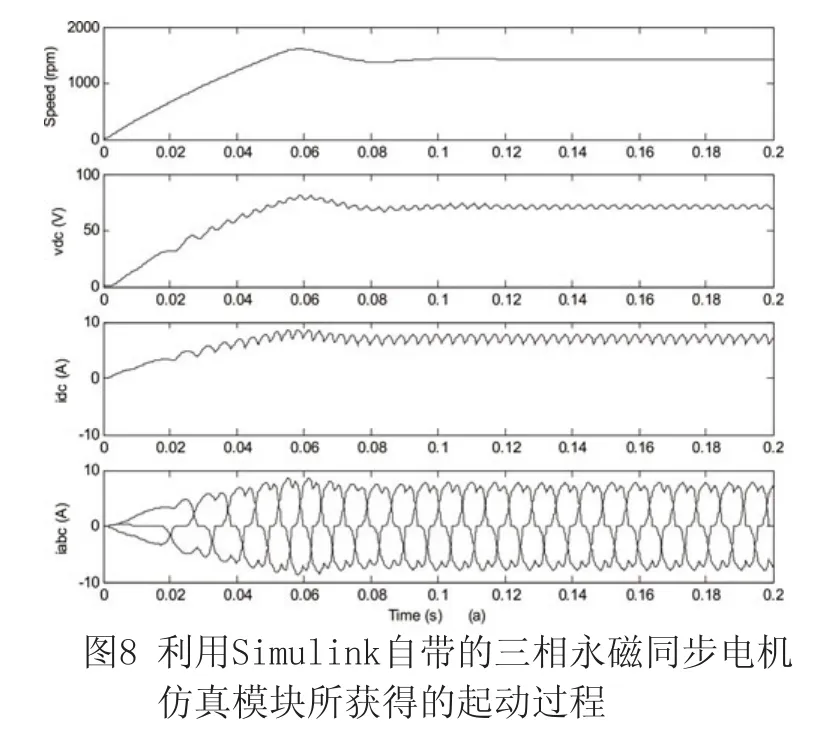
图7是电机 x-y-z 绕组开路时的系统起动过程。从中可明显看到直流侧电压和电流的纹波变大了。其原因是此时直流侧电压/电流最低次谐波已由12次降为6次,谐波幅值则按反比关系相应增大。在外围参数完全不变的情况下,将所建六相电机模型更换成Simulink提供的标准三相凸极永磁同步电机仿真模型,设置其直/交轴电感参数为5 mH和8 mH以便与六相电机电感参数相吻合,其它参数则完全与表2一致。图8给出了此时所获得的系统起动过程仿真波形。可见图8与图7完全一致。值得指出的是,为了与Simulink库模型中转子位置角初始值保持一致,在以上仿真中本文所建电机模型的转子位置角初始值均设置为负90°。
4 结论
在Matlab/Simulink仿真环境下建立了六相凸极永磁同步电机——变流器系统的仿真模型。其中电机模型以描述电机 d1-q1-d2-q2坐标系数学模型的S函数以及配套的坐标变换阵为核心,外加合适的电压检测与受控电流源等基本Simulink电路仿真模块构成与变流器的电气接口。该模型结构简单,易于实施,仿真结果可信,可用于微型燃气轮机发电系统的研究。
:
[1]T.M. Jahns. Improved reliability in solid-state ac drives by means of multiple independent phase-drive units.IEEE Trans. Ind. App., 1980, IA-16(3):321-331.
[2]P. Ferraris and M. Lazzari. Phase numbers and their related effects on the characteristics of inverter fed induction motor drives. Conf. Rec. of IEEE IAS’,1983:494-502.
[3]M.A. Abbas, R. Chisten, and T.M. Jahns.Six-phase voltage source inverter driven induction motor. IEEE Trans. Ind. App., 1984, IA-20(5): 1251-1259.
[4]H.A. Toliyat, R. Shi, and H. Xu. A DSP-based vector control of five-phase synchronous reluctance motor.Conf. Rec. of IEEE IAS’2000.
[5]S.D. Pekarek, O. Wasynczuk, and H.J. Hegner. An efficient and accurate model for the simulation and analysis of synchronous machine/converter systems.IEEE Trans. on Energy Conversion, 1998, 13(1):42-48.
