地震的“序列归属”问题与ETAS模型——以唐山序列为例
2013-08-09蒋长胜吴忠良庄建仓
蒋长胜,吴忠良,庄建仓
1 中国地震局地球物理研究所,北京 100081
2 统计数理研究所,日本东京都立川市绿町 10-3190-8562
1 引 言
一次中小地震发生后,其“序列归属”问题——即这次地震究竟是此前发生的某一地震的余震,还是一次独立的“背景”地震,是公众和地震学家都十分关注的问题.这个问题对“时间相依的地震危险性”(time-dependent seismic hazard)的判断有重要的参考价值.正在进行之中的国际“地震可预测性合作研 究”(Collaboratory for the Study of Earthquake Predictability,CSEP)计划(http://www.cseptesting.org[2012-04-25])中,包括了用一日至数日尺度的短期地震概率预测模型对余震进行实际的向前概率预测的工作.这些短期预测模型包括用于美国加州地区的STEP模型[1]、意大利地区的ETES和ERS模型[2],以及日本地区的 ETAS模型[3]等等.对这些模型进行检验的一个重要的基础性指标,就是对地震“序列归属”的判断.
余震活动的持续时间问题一直是地球动力学和地震物理中的一个有意义的问题[4-7],因为余震活动的持续时间是地球动力学中为数不多的可以在观测仪器记录的时间尺度上通过测量来准确把握的物理量之一.一般说来,强震发生后经过的时间越长,震中区地震活动的“序列归属”问题就越复杂.在距强震发生的时间长到一定程度的时候,判断余震序列在何时开始“混同于”当地的“背景地震活动”,成为一个复杂的问题.
传统意义上的“余震”,指发生在主震之后、震级小于主震的地震事件[8],而地震活动在时间和空间分布上具有高度的不均匀性,地震丛集与“正常”的背景地震活动往往叠加在一起,传统上的前震、主震和余震在物理本质和统计属性上均难以区分[9].因此在一定意义上说,地震的“序列归属”问题几乎不存在一个确定性的答案.然而近年来,描述复杂地震活动的“传染型余震序列”(ETAS)模型[10]得到较大发展,ETAS模型不再区分前震、主震和余震,认为任何地震都有可能被之前发生的地震所触发,并用概率形式来描述其作为背景地震或丛集地震的可能.这就为“序列归属”问题的解决提供了另一个有效的工作思路.
本文试图将这一模型应用于中小地震的“序列归属”问题.我们选取唐山序列作为实例,这一序列从1976年唐山大地震至今,已持续30余年时间.相应的“序列归属”问题,甚至引起社会公众的广泛关注和 激 烈 争 论 (http://news.sina.com.cn/c/p/2012-05-29/020524495099. shtml; http://news.sohu.com/20120529/n344307586.shtml[2012-04-25]).我们使用随机除丛法[11-12]从时间和空间上同时分离“背景地震”和“丛集地震”.作为一个应用实例,本文考察了2010年以来三次MS4.0级地震与唐山地震序列的关系.
2 基于时-空ETAS模型的随机除丛法
目前已有多种分支过程(branching processes)模型用于描述地震活动的时 空丛集特征[10,13-15].基于点分支过程理论的ETAS模型推广了大森定律[16],假定每一个地震总能以一定的概率规则独立地触发“子震”,来描述地震活动时-空丛集结构[10,17-18].Ogata[19]给出的时-空 ETAS模型将地震发生率λ表示为:

这里的μ(x,y)为背景地震活动强度,即“背景”地震发生率,是与时间无关的空间位置的函数.κ(m)表示的是震级为m的事件触发子震数目的期望;g(t)和f(x,y;m)分别为子震的时间与空间概率密度函数,分别可采用如下形式表示[12]:
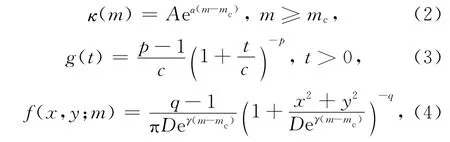
其中A、α、p、q、D、γ和c为常数,mc为计算的截止震级.另外假定震级的概率密度函数为

这里的β与Gutenberg-Richter定律中的b值关系为β=bln10.在Zhuang等[11]与Zhuang和 Ogata[12]发展的随机除丛法中,地震i对其后发生的地震j处(tj,xj,yj)的地震发生率的相对贡献或触发地震j的概率可表示为

这里的
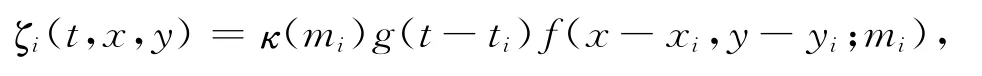
而地震j作为背景地震的概率为

由背景地震概率可用核函数法来估算地震背景活动强度μ(x,y):

其中T为研究时段长度,Zhj是带宽为hj的高斯核函数.带宽变量hj是地震j到第np个最近地震的距离.根据一般做法[11-12],设置np=4.
对于实际的地震目录{(ti,xi,yi,mi):i=1,2,…,N},如果给定强度函数u(x,y),背景地震活动强度可表示为μ(x,y)=vu(x,y),其中v为大于0的待估参数,并可利用最大似然法来估计公式(1)中的各项参数.再由(7)式求得每个地震的背景地震概率φ后,利用(8)式重新计算u(x,y),并反复迭代直至结果收敛,即可同时求取背景地震活动强度μ(x,y)和模型参 数 {v,A,α,p,q,D,γ,c}.不同 于传统删除余震算法[20-21],时-空 ETAS模型考虑了全部历史地震的综合触发效应,地震丛集也不仅包括余震,还包括传统意义上的前震和震群.
3 研究区域和计算所用资料
本文的研究区域为38.5°N—41.0°N,116.9°E—120.0°E的唐山地区,空间上包括了1976年7月28日唐山MS7.8地震的余震分布区域.资料使用了中国地震台网中心提供的1970年1月1日至2008年12月31日的《中国微震目录》和2009年1月1日至2012年6月1日的《中国地震台网统一地震目录》.该目录根据国家台网和各区域台网测定资料汇编而成,震级单位统一为地方震震级ML.唐山MS7.8地震发生后,余震区地震活动强烈,据《唐山地震目录》[22]统计,自主震发生至1979年12月31日共记录唐山地震序列ML2.0以上地震14425次,其中包括1976年7月28日滦县MS7.1和11月15日宁河MS6.9地震,近年来相继发生2010年3月6日河北滦县MS4.3、4月9日河北丰南MS4.1和2012年5月28日河北唐山、滦县交界MS4.8等中等地震.图1给出了研究区1970年以来ML4.0以上地震的震中分布.
关于地震目录的完整性[23]的研究表明,强震发生后,由于主震面波振幅较大、降低了地震记录的信噪比,往往导致主震后数小时区域甚至全球的地震监测能力的下降[24].鉴于当时地震观测条件有限和唐山MS7.8地震发生后震中附近台站的损坏,对研究区地震监测能力的变化需要重点考虑.本研究从定性分析和定量研究两方面来考察.研究中采用了震级-序号法[25]定性讨论研究区内最小完整性震级Mc的时序变化.震级-序号法按地震发生时间的先后顺序排序,地震密度较大的区域的连线大致为Mc的时序变化,这种分析一方面避免了主震发生后短期内余震较为密集,按时间统计难以分析余震监测能力的变化,另一方面,由于地震监测能力在短期内的变化常具有分段和不连续性,由此可能给出地震记录信噪比和人为因素引起的监测能力变化.结果如图2a所示,1976年唐山MS7.8地震发生后,Mc仅为ML4.0左右,其后至1987年左右,研究区的地震监测能力显著提升,Mc已低于ML2.0.此外,研究中还使用了“最大曲率”MAXC方法和拟合度分别为90%和95%的GFT方法[26]来定量评估研究区Mc的时序变化.其中MAXC方法是将震级-频度分布曲线的一阶导数的最大值对应的震级作为Mc,而GFT方法是通过搜索对应给定的实际和理论震级-频度分布下的拟合度百分比来确定Mc.计算中使用固定为500个地震事件的窗口选取数据,并滑动计算,结果如图2b所示.与图2a定性分析结果非常一致的是,研究区1970年以来ML4.0以上的地震较为完整,本研究将 Mc=ML4.0作为时-空ETAS模型分析的截止震级.
4 “背景”地震概率和被“母震”触发的概率
研究中通过最大似然法,估计唐山地区时-空ETAS模型的参数,求取1970年以来每个ML4.0以上的地震作为孤立/背景地震的概率φ,此外,还可获得任一地震被之前发生的“母震”触发的概率ρ.对研究区1970年以来ML4.0以上地震的ETAS模型参数估计结果如表1所示,计算获得的每个ML4.0以上地震的背景地震概率φ的空间分布如图3所示.由图3可见,1976年唐山MS7.8地震余震区绝大多数地震的背景地震概率φ<0.5,即表明研究区内地震多数为丛集地震.但对于2010年以来余震区发生的3次MS4.0以上地震,背景地震概率φ分别为0.72、0.88和0.76,表明其作为孤立地震的概率较高,也意味着它们被之前发生的地震,包括1976年唐山MS7.8地震所直接触发的概率较低.

表1 唐山地区1970年以来ML4.0以上地震的时-空ETAS模型参数拟合结果Table 1 Parameters from fitting the ETAS model to seismicity above ML4.0in the Tangshan region since 1970
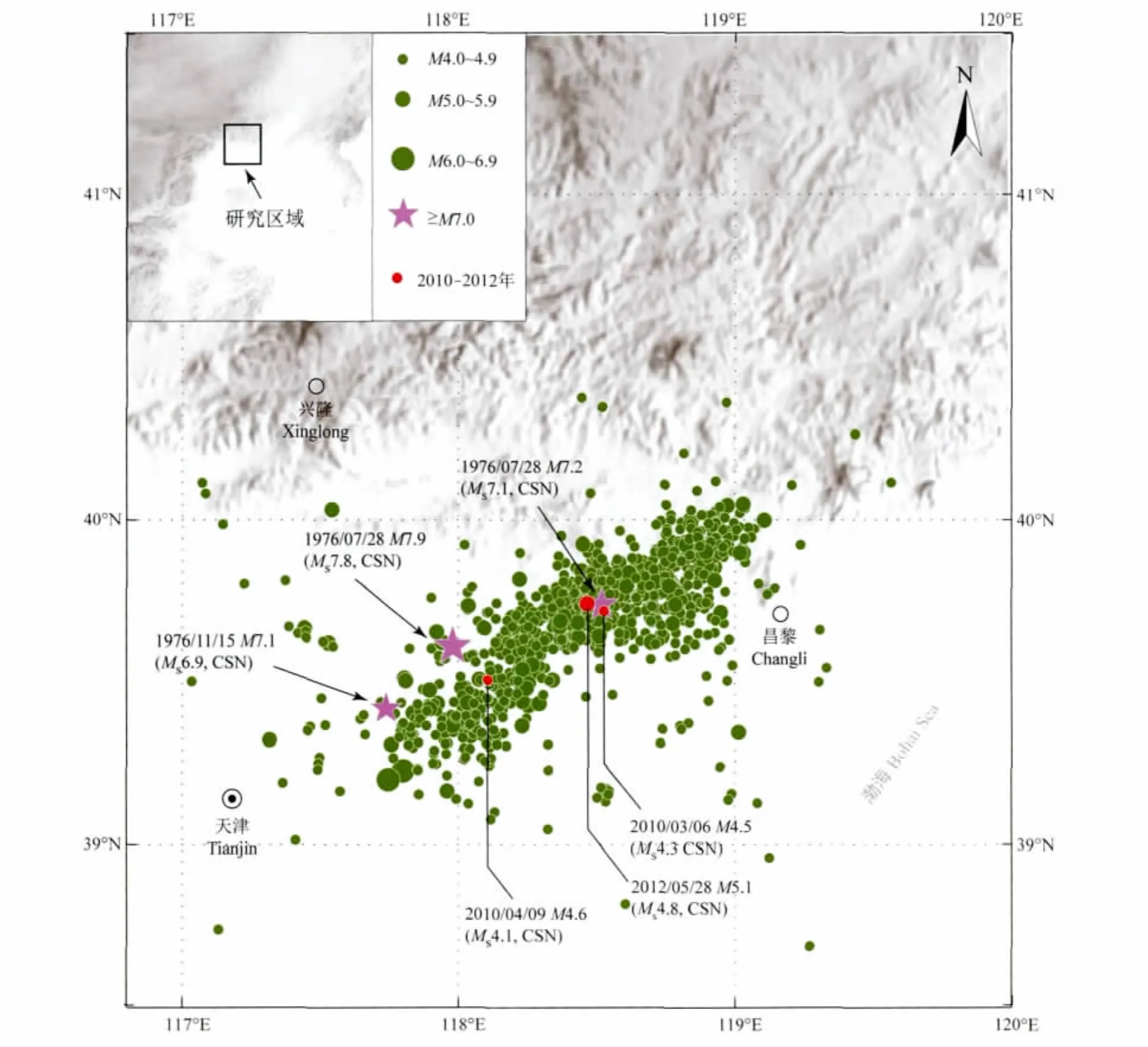
图1 唐山地区1970年以来ML4.0以上地震分布图中紫色五角星标出了3次较大地震事件,即1976年唐山MS7.8、滦县MS7.1、宁河MS6.9地震的位置,红色实心圆标出了2010年以来3次MS4.0以上地震的位置.左上角子图给出了研究区的空间位置示意图.Fig.1 Distribution of earthquakes above ML4.0in the Tangshan region since 1970The purple pentacles show the three major events,namely the Tangshan MS7.8earthquake,the Luanxian MS7.1earthquake,and the Ninghe MS6.9earthquake.The red circles indicate the three events above MS4.0since 2010.Parameters of these events are marked in the figure.The geographical location of the study region is shown in the upper-left inset panel.
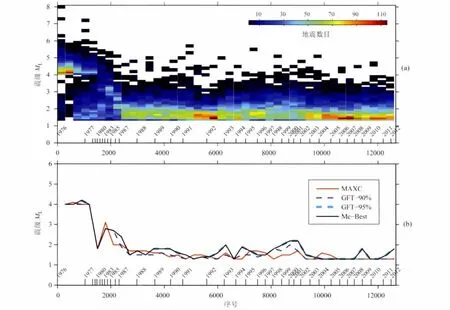
图2 唐山地区1970年以来地震目录的完整性分析(a)震级序号法给出的地震密度分布;(b)多统计方法定量分析给出的最小完整性震级Mc的时间变化,由于同时采用90%和95%的拟合度GFT方法,这里分别称为GFT-95%和GFT-90%以示区别.图中采用了地震发生先后顺序作为横坐标,不等间隔的地震发生时间也被标在横坐标上方.Fig.2 Catalogue completeness analysis for the Tangshan region since 1970(a)Seismic rate for different magnitudes in the index domain;(b)Completeness thresholds Mcestimated by using MAXC (red solid line),90%GFT (black dashed line),95%GFT (blue dashed line)and Mc-Best(black solid line)method.See text for details.
研究区ML4.0以上地震的背景地震概率φ的时间分析如图4所示,其中图4a为震级-时间图(M-t图),图4b为与各次地震相对应的背景地震概率φ.由图可见,1976年唐山MS7.8地震发生前,除一次地震事件φ<0.5外,其他事件的φ均大于0.9,可能与这些地震事件分布较为分散有关.而MS7.8地震的φ也接近于1,表明其无明显的前震事件存在.1976年唐山MS7.8地震发生后至1997年之前,除个别地震外,绝大多数地震的φ<0.5,表明被触发的概率较高.而1997年之后,除个别地震紧跟之前地震发生,φ接近0外,其他地震事件φ均大于0.5,表明它们作为背景地震或孤立地震的概率较高,与其之前发生的地震,包括1976年唐山MS7.8地震的关系较小.因此,如以φ0=0.5作为背景地震的定义,从时-空EIAS模型拟合结果上来看,唐山地区1997年之后发生的ML4.0以上地震,在ETAS模型的意义上也许不能再称之为1976年唐山MS7.8地震的余震了.
以新近发生的2012年MS4.8地震为例,考察其被 “母震”触发的概率ρ,结果如图4c所示.由图可见,包括1976年唐山MS7.8地震在内的“母震”,对2012年MS4.8地震的触发概率远小于参考概率ρ0=0.5,其中触发概率最高的为2010年河北滦县MS4.3地震,ρ=0.0234.由此可见,2012年 MS4.8地震也许不能简单看成之前发生的地震,包括1976年唐山MS7.8地震的直接余震.
如果唐山地区1997年之后发生的ML4.0以上地震不能称之为1976年MS7.8地震的直接余震,由此引发的问题是,唐山MS7.8地震的序列是如何构成的?为考察此问题,对研究区内的ML4.0以上地震分别使用不同的被1976年唐山MS7.8地震触发的概率阈值,构建MS7.8地震的序列.图5给出了MS7.8地震之后发生的地震相对于1976年7月28日00∶00∶00的时间间隔与其经度的分布图,由图可见,除MS7.8地震发生后数小时内的地震外,序列中被MS7.8地震触发的概率已经显著降低至0.5以下.由此表明,余震区内95%以上的地震与MS7.8地震的直接关联较小,而更可能是被MS7.8地震的余震,或余震的余震所触发——关于这一结果,也许还可以有另一种解释,参见讨论一节.

图3 时-空ETAS模型给出的唐山地区背景地震概率φ的空间分布图中分别用渐变的红色和蓝色表示φ≥0.5和φ<0.5的情况.Fig.3 Spatial distribution of background probabilityφby fitting the space-time ETAS modelThe gradually changing blue and red colors indicate the events withφ≥0.5andφ<0.5,respectively.
5 截止震级选取和地震目录误差对结果的影响
由于早期监测能力等方面的原因,在本研究中使用了唐山地区ML4.0以上地震拟合时-空ETAS模型.由于任何一个地震都可以以一定概率触发后续地震,低于ML4.0的大量的较小震级事件将可能显著改变包括2010年滦县MS4.3、丰南MS4.1和2012年MS4.8地震的背景地震概率,因此,这些唐山地区较晚发生的地震事件作为孤立的背景地震只是相对的.为进一步验证此问题,本研究采用不同的截止震级分别对时-空ETAS模型进行拟合,并求取背景地震概率,结果如表2所示.
图6给出了时-空ETAS模型参数拟合中使用不同截止震级Mc,对2010年以来3次MS4.0以上地震的背景地震概率φ以及被1976年唐山MS7.8地震触发的概率ρ的影响.图6a显示,当降低Mc时,2010年以来3次MS4.0以上地震的φ值随之降低,表明随着参与计算的地震数目的增多,增加了被触发的可能;而图6b给出的Mc与被MS7.8地震触发的概率ρ的图像显示,随着Mc的减小,这些发生较晚的地震被MS7.8地震触发的概率也随之减小.这些现象与 Wang等[27]对ETAS模型中小震级事件缺失造成的影响的测试结果是相一致的.由此可进一步外推,当能够获得更为完整的历史地震记录、更多的小震级事件参与时-空ETAS模型拟合的情
况下,唐山地区类似于2010年以来3次MS4.0以上较晚发生的地震,将很难保证其作为背景地震,但与1976年唐山MS7.8地震的直接关联也随之减小.

表2 唐山地区1970年以来不同截止震级的时-空ETAS模型参数拟合结果Table 2 Results from fitting the ETAS model to earthquake data from Tangshan region since 1970,with different cutoff magnitudes
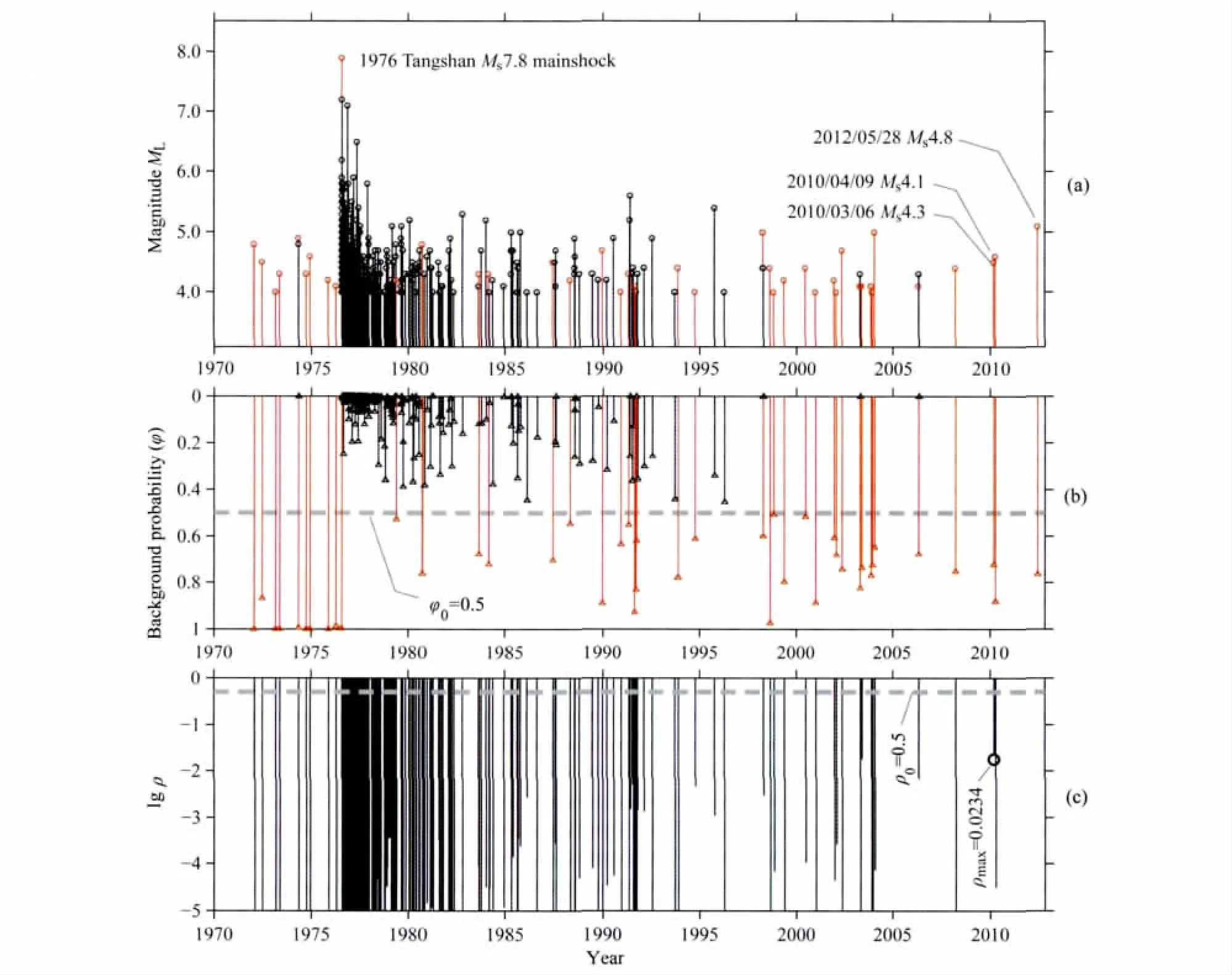
图4 唐山地震序列的背景地震概率φ时间分布(a)唐山地震序列的震级-时间(M-t)图,及其(b)各事件对应的背景地震概率φ;(c)2012年5月28日MS4.8地震被之前发生地震触发的概率ρ,其中触发概率最高的为与其时、空上最为接近的2010年3月6日MS4.3地震,图中水平虚线标出了参考线ρ0=0.5的位置.Fig.4 Temporal variation of background probabilityφof the Tangshan sequence(a)Temporal distribution of magnitudes of the Tangshan sequence;(b)Background probabilityφvarying with time;(c)Temporal distribution of the probabilityρfor being triggered by previous events,for the May 28,2012,Tangshan MS4.8earthquake,with the maximum value ofρcorresponding to the March 6,2010,Luanxian MS4.3earthquake,the nearest one in time and space.The horizontal dashed line shows the reference levelρ0=0.5.


此外,由于地震目录中事件参数的测定误差是不可避免的,可能对统计地震学计算结果产生影响,对此可采用生成随机地震目录的方式考察结果的稳健性[28-29].除考虑不同截止震级 Mc的影响外,本文还考虑了地震目录中的震级和定位测定误差的可能影响.其中,分别对唐山地震序列的震级叠加了范围在[-0.3,0.3]之间的随机误差,对序列中事件的水平位置叠加了范围在[-5km,5km]之间的随机误差,各生成100个随机目录并进行时-空ETAS模型拟合,结果如图7所示.由图可见,在考虑了0.3个震级单位和定位±5km的误差情况下,2010年以来3次MS4.0以上地震的背景地震φ和被唐山MS7.8地震触发的概率ρ均有不同程度的离散,其中定位误差对拟合结果的离散程度大于震级的影响.但综合来看,上述稳健性测试表明,唐山地震序列中的参数测定误差不改变2010年以来3次MS4.0以上地震作为背景地震和被唐山MS7.8地震低概率触发的认识.

图7 震级和震中位置测定误差对时-空ETAS模型计算结果的影响(a)震级测定误差对估算背景地震概率φ的影响;(b)震级测定误差对被1976年MS7.8地震触发的概率ρ的影响;(c)震中位置测定误差对估算背景地震概率φ的影响;(d)震中位置测定误差对被1976年MS7.8地震触发的概率ρ的影响.图中垂直虚线分别对应2010年以来3次MS4.0以上地震在未考虑震级和震中位置测定误差情况下的计算结果.Fig.7 Influences of magnitude uncertainties and locations uncertainties on the estimates of the declustering probabilities related to the three earthquakes with magnitude larger than Ms4.0since 2010in the Tangshan sequence(a)Background probabilityφaffected by the uncertainty of magnitude;(b)Probabilityρof being triggered by the 1976Tangshan MS7.8 mainshock,affected by the uncertainty of magnitude;(c)Background probabilityφaffected by the uncertainty of location;(b)Probability ρof being triggered by the 1976Tangshan MS7.8mainshock,affected by the uncertainty of location.The vertical dashed lines show the fitting results of the three events with magnitude larger than MS4.0since 2010,without the influence of the uncertainties of magnitude and location.
6 讨论和结论
本文采用了当前能够较好描述复杂地震活动特征的时-空ETAS模型,对唐山余震区1970年以来ML4.0以上地震进行了分析.利用拟合结果中的背景地震概率φ和被“母震”触发的概率ρ,讨论了2010年以来发生的三次MS4.0以上中小地震的“序列归属”(ESA)问题.结果表明,从背景地震概率来看,唐山地区1997年之后发生的ML4.0以上地震的φ较高,其中2010年以来三次MS4.0以上地震分别可达0.72、0.88和0.76.从标准的ETAS模型所能得到的结果显示,唐山余震区内绝大多数地震与1976年MS7.8地震的直接关联较小,后续发生的地震更可能是被MS7.8地震的余震,或余震的余震所触发的.
由于地震观测能力的限制,目前尚无法无限降低计算所用的截止震级,因此在ETAS模型研究中的“背景地震”仅为相对概念,与截止震级和所讨论的震级范围有关.研究中为降低时-空ETAS模型的复杂性,采用了背景地震发生率是平稳的、与时间无关的假定.而目前一些工作也在从不同层面讨论背景地震的时间变化[30-32]和空间变化[33].
另外,ETAS模型在实际应用时也许还应考虑一个地震学问题:对于一次接近8级的地震,有限的震源尺度,已经不允许震源再作为一个“点源”.对于唐山地震,在ETAS模型中的“距离”(公式(4)中的x2+y2),也许不应是距主震震中的距离,而(至少)应是距主震断层面的距离[34].此外将一次接近8级的地震的矩释放“集中”于震中是否是一个物理上合理的处理,也是值得讨论的.也许与“被余震触发”的情况大致等效的,应该是不止以一个主震的震中,而是以一系列代表了主要“凹凸体”的“等效地震”的震中,来描述主震.但是有一点也许是清楚的,就是目前距主震的发生毕竟已经有太长的时间,因此即使距离主震震中位置很近的2010/2012年的地震,其属于“背景”地震序列的概率也是很高的——即使主震的位置被赋予了过多的矩释放量.
1976年唐山MS7.8地震的余震时、空活动较为复杂,余震展布在140km长、分段特征明显的断层上[35],序列中的较大余震分别呈现了走滑、正断和逆冲等不同的机制类型[36],而序列的地震活动也兼有主余型和震群型的特征[37].也许考虑中小地震的震源机制和主震的破裂过程,辅之以CFS的计算,还会得到更多的信息.当然,也有些研究者认为,唐山地震及相关地震的发生,可能与太平洋板块深俯冲至我国东部下方的地幔转换带,然后滞留脱水造成热物质上涌并在地壳深部形成流体,作用于唐山地区断裂带有关[38].对上述问题的讨论应为本研究的后续工作.
(References)
[1]Gerstenberger M C,Wiemer S,Jones L M,et al.Real-time forecasts of tomorrow′s earthquakes in California.Nature,2005,435(7040):328-331.
[2]Falcone G,Console R,Murru M.Short-term and long-term earthquake occurrence models for Italy:ETES,ERS and LTST.Annals of Geophysics,2010,53(3):41-50.
[3]Zhuang J C.Next-day earthquake forecasts for the Japan region generated by the ETAS model.Earth Planets Space,2011,63(3):207-216.
[4]Dieterich J. A constitutive law for rate of earthquake production and its application to earthquake clustering.J.Geophys.Res.,1994,99(B2):2601-2618.
[5]Li L,Chen Q F,Cheng X,et al.Spatial clustering and repeating of seismic events observed along the 1976Tangshan fault,north China.Geophys.Res.Lett.,2007,34(23):L23309,doi:10.1029/2007GL031594.
[6]Stein S,Liu M.Long aftershock sequences within continents and implications for earthquake hazard assessment.Nature,2009,462(7269):87-89.
[7]Castro R R,Shearer P M,Astiz L,et al.The long-lasting aftershock series of the 3May 1887 Mw7.5Sonora earthquake in the Mexican Basin and Range Province.Bull.Seismol.Soc.Am.,2010,100(3):1153-1164.
[8]Keilis-Borok V I,Knopoff L,Rowain M I.Bursts of aftershocks,long-term precursors of strong earthquakes.Nature,1980,283(5744):259-263.
[9]Helmstetter A,Sornette D. Foreshocks explained by cascades of triggered seismicity.J.Geophys.Res.,2003,108(B10):2457,doi:10.1029/2003JB002409.
[10]Ogata Y.Statistical models for earthquake occurrences and residual analysis for point processes.J.Am.Stat.Assoc.,1988,83(401):9-27.
[11]Zhuang J C,Ogata Y,Vere-Jones D.Stochastic declustering of space-time earthquake occurrences.J.Am.Stat.Assoc.,2002,97(458):369-380.
[12]Zhuang J C, Ogata Y.Properties of the probability distribution associated with the largest event in an earthquake cluster and their implications to foreshocks.Physical Review E.Stat.Nonlin Soft.Matter.Phys.,2006,73(4):046134,doi:10.1103/PhysRevE.73.046134.
[13]Kagan Y Y.Likelihood analysis of earthquake catalogues.Geophys.J.Int.,1991,106(1):135-148.
[14]Musmeci F,Vere-Jones D.A space-time clustering model for historical earthquakes.Ann.Inst.Stat.Math.,1992,44(1):1-11.
[15]Console R,Murru M.A simple and testable model for earthquake clustering.J.Geophys.Res.,2001,106(B5):8699-8711.
[16]Omori F.On the aftershocks of earthquakes.J.Coll.Sci.Imp.Univ.Tokyo,1894,7:11-200.
[17]Ogata Y.Statistical model for standard seismicity and detection of anomalies by residual analysis.Tectonophysics,1989,169(1-3):159-174.
[18]Ogata Y.Increased probability of large earthquakes near aftershock regions with relative quiescence.J.Geophys.Res.,2001,106(B5):8729-8744.
[19]Ogata Y.Space-time point-process models for earthquake occurrences.AnnalsoftheInstituteofStatistical Mathematics,1998,50(2):379-402.
[20]Gardner J K,Knopoff L.Is the sequence of earthquakes in Southern California,with aftershocks removed,Poissonian?Bull.Seismol.Soc.Am.,1974,64(5):1363-1367.
[21]Reasenberg P.Second-order moment of central California Seismicity,1969—1982.J.Geophys.Res.,1985,90(B7):5479-5495.
[22]河北省地震局.唐山地震目录.北京:地震出版社,1981:1-632.Hebei Seismological Bureau. Catalogue of Tangshan Earthquake(in Chinese).Beijing:Earthquake Press,1981:1-632.
[23]Woessner J,Wiemer S.Assessing the quality of earthquake catalogues:estimating the magnitude of completeness and its uncertainty.Bull.Seismol.Soc.Am.,2005,95(2):684-698.
[24]Iwata T.Low detection capability of global earthquakes after the occurrence of large earthquakes:investigation of the Harvard CMT catalogue.Geophys.J.Int.,2008,174(3):849-856.
[25]Ogata Y,Imoto M,Katsura K.3-D spatial variation of bvalues of magnitude-frequency distribution beneath the Kanto district,Japan.Geophys.J.Int.,1991,104(1):135-146.
[26]Wiemer S,Wyss M.Minimum magnitude of completeness in earthquake catalogs:examples from Alaska,the Western United States,and Japan.Bull.Seismol.Soc.Am.,2000,90(4):859-869.
[27]Wang Q,Jackson D D,Zhuang J C.Missing links in earthquake clustering models.Geophys.Res.Lett.,2010,37(21):L21307,doi:10.1029/2010GL044858.
[28]Huang Q H.Search for reliable precursors:A case study of the seismic quiescence of the 2000western Tottori prefecture earthquake.J.Geophys.Res.,2006,111(B4):B04301,doi:10.1029/2005JB003982.
[29]Zhou S Y,Johnston S,Robinson R,et al.Tests of the precursory AMR using a synthetic seismicity model.J.Geophys.Res.,2006,111:B05308,doi:10.1029/2005JB003720.
[30]Hainzl S,Ogata Y.Detecting fluid signals in seismicity data through statistical earthquake modeling.J.Geophys.Res.,2005,110(B5):B05S07,doi:10.1029/2004JB003247.
[31]蒋海昆,杨马陵,孙学军等.暴雨触发局部地震活动的一个典型例子:2010年6月广西凌云—凤山交界3级震群活动.地球物理学报,2011,54(10):2606-2619.Jiang H K,Yang M L,Sun X J,et al.A typical example of locally triggered seismicity in the boundary area of Lingyun and Fengshan following the large rainfall event of June 2010.Chinese J.Geophys.(in Chinese),2011,54(10):2606-2619.
[32]Peng Y J,Zhou S Y,Zhuang J C,et al.An approach to detect the abnormal seismicity increase in Southwestern China triggered co-seismically by 2004Sumatra Mw9.2earthquake.Geophys.J.Int.,2012,189(3):1734-1740.
[33]Tsukakoshi Y,Shimazaki K.Temporal behavior of the background seismicity rate in central Japan,1998to mid-2003.Tectonophysics,2006,417(1-2):155-168.
[34]Marsan D,LenglinéO.A new estimation of the decay of aftershock density with distance to the mainshock.J.Geophys.Res.,2010,115(B9):B09302,doi:10.1029/2009JB007119.
[35]Butler R,Stewart G S,Kanamori H.The July 27,1976 Tangshan,China earthquake—a complex sequence of intraplate events.Bull.Seismol.Soc.Am.,1979,69(1):207-220.
[36]Shedlock K M,Baranowski J,Xiao W W,et al.The Tangshan aftershock sequence.J.Geophys.Res.,1978,92(B3):2791-2803.
[37]吴开统,王泽皋,吕培苓.地震参数与序列,一九七六年唐山地震.北京:地震出版社,1982:65-66.Wu K T,Wang Z G,LüP L.Earthquake Parameters and Sequence,1976Tangshan Earthquake(in Chinese).Beijing:Earthquake Press,1982:65-66.
[38]Lei X L,Xue Z Q.Ultrasonic velocity and attenuation during CO2injection into water-saturated porous sandstone:Measurements using difference seismic tomography.Phys.Earth Planet.Inter.,2009,176(3-4):224-234.
