修建成本不确定的交通网络设计问题

谢桃枫,陈国庆*,曹瑾鑫

(内蒙古大学a.数学科学学院,呼和浩特010021;b.交通学院运输工程系,呼和浩特010070)

修建成本不确定的交通网络设计问题

谢桃枫a,陈国庆*a,曹瑾鑫b

(内蒙古大学a.数学科学学院,呼和浩特010021;b.交通学院运输工程系,呼和浩特010070)

交通网络设计问题是交通规划理论的一个重要组成部分,即在资金有限且考虑出行者决策行为的情况下,制定最优投资策略.由于人工费、材料费和使用费等的不确定性,路段的修建成本存在不确定性.本文通过改进预算投资约束,应用鲁棒优化的方法同时考虑出行者的路径选择行为,建立路段修建成本不确定的交通网络设计的鲁棒模型,并利用基于割约束的混合整数线性规划算法求解此模型,进而得到一个受修建成本扰动较小的鲁棒最优解.通过算例表明,在修建成本不确定的交通网络设计中,本文提出的鲁棒优化方法可以得到比传统确定性问题更加可靠的解.

城市交通;不确定混合整数线性规划;不确定投资成本;鲁棒优化法;交通网络设计

1 引 言

交通网络设计问题的主要目标是通过对现有交通网络增加新的路段或提高已有路段的通行能力,从而使整个交通网络某种系统性能达到最优.一般来说,交通网络设计问题可分为三类,即连续交通网络设计问题、离散交通网络设计问题和混合交通网络设计问题.长期以来,交通网络设计问题一直被认为是交通研究领域中难度最大的问题之一.目前在交通网络设计问题方面,国内外已经有许多学者做过大量的研究,并设计了求解算法.

Sumalee在路段的造价方面,利用GA-AS算法进行求解[1].Meng把双层规划模型利用临界价值函数转化为连续可微的单层规划模型,且用增广拉格朗日算法寻找精确局部解[2].Wang针对连续网络设计问题进行讨论,通过把双层规划问题近似为一个混合整数线性规划问题来寻找近似全局最优解[3].此方法是先对非线性函数离散化,再用线性函数近似非线性函数.Edmunds和Bard针对双层规划问题进行研究,文中要求下层模型的目标函数是凸二次函数,所有的约束条件都是线性的,再利用分支定界法对混合整数非线性双层规划模型求解全局最优解[4].Luathep把文献[3]中的连续交通网络设计问题推广到混合交通网络设计问题中,把混合非线性网络设计问题利用分段线性法转化为混合整数线性规划问题,最终得到近似全局最优解或近似全局最优解的上界[5].

近年来,不确定交通网络设计问题主要集中于对不确定需求的研究.Yin和Lawpongpanich研究不确定需求下的静态连续均衡的网络设计问题[6].Ordonez和Zhao制定和解决了一个静态的网络设计模型,其需求和旅行时间控制在一个静态的多面体集合中[7].Mudchanatongsuk等延续了Ordonez和Zhao的工作,通过考虑一些不确定需求的推广假设,研究一个道路约束的网络设计问题,并引入列生成方法解决带有多面体不确定集合的鲁棒网络设计问题[8].Ban等认为鲁棒道路收费问题包含多个流量分配方案[9].Yin等确定了需求不确定条件下的鲁棒优化道路网络改善计划[10].Lou等描述了一个离散网络设计问题,用户均衡流是基于不确定预算的概念,利用切平面法求解问题[11].

在文献[5]中,预算投资约束是用一个简单线性函数表示,即每一条路段的修建成本是确定的.由于人工费、材料费和使用费等的不确定性,路段的修建成本存在不确定性.为了克服现有方法在处理投资成本不确定性方面的局限性,通过改进预算投资约束,本文提出了基于鲁棒优化方法的投资成本不确定的交通网络设计问题,利用割约束的混合整数线性规划算法对模型进行求解.通过算例证明鲁棒优化方法可以得到比传统确定性优化方法更可靠的解.

2 主要符号说明

A1——不扩建道路的集合;

A2——扩建道路的集合;

A3——新建道路的集合;

A——道路的集合,A=A1∪A2∪A3,|A|=α;

ℜ——交通网络节点的集合,ℜ =R;

O——所有起点的集合,O⊆ℜ;

D——所有终点的集合,D⊆ℜ;

ℌ——凸多面体的极点的集合;

ℑ——指标集,ℑ={0,…,M,M+1,…,M +N};

o——起点,o∈O;

d——终点,d∈D;

s——极点指标,s∈ℌ;

xa——第a条道路的流量,∀a∈A;

xsa——凸多面体的第s个极点,∀a∈A;

qod——起点o至终点d的出行需求;

vod——起点o至终点d路段a的流量,∀a∈A;

a

ya——扩建道路a增加的容量,∀a∈A2;

y*——新建道路a的固定容量,∀a∈A;

a3

x-——路段a的最大流量,∀a∈A;

a

y-a——扩建道路a的原始容量,∀a∈A2; y-——扩建道路a后增加的容量,∀a∈A;

a2

y-*——新建道路a的最大容量,∀a∈A;

a

3

X——路段流量组成的向量;

Qod——起点o至终点d的出行需求形成的R ×1向量;

vod——起点o至终点d路段流量的向量;

Λ——由发生变量组成的R×α发生矩阵;

χa——

g(ya)——扩建道路的价值函数,∀a∈A3;

ta(xa)——没有扩建道路的出行时间函数,∀a∈A1;

ta(xa,ya)——扩建道路的出行时间函数,∀a∈A2;

ta(xa,y*

a)——新建道路的出行时间函数,∀a∈A3;

tij(xij)——起点是i,终点是j的道路的出行时间;

t0——起点是i,终点是j的道路的自由出行

ij时间;

在利用分段函数线性化时,引入如下变量:

M——对xa分M段;

N——对ya分N段;

λma——∀a∈A1∪A3;

κma——∀a∈A1∪A3;

μma——SOS1变量,即至多有一个变量是正值,其他都为零,μma∈ [0,1],∀m=1,2,…, M,a∈A2;

υna——SOS1变量,υna∈[0,1],∀n=1,2,…,N,a∈A2;

Γηa——SOS2变量,至多有两个变量是非零值,若两个值是正值,则这两个值是相邻的,∀η∈ℑ,a∈A2;

γm,n——连续变量,γm,n∈[0,1],∀m=1,aa…,M,n=1,…,N,a∈A2,

φa——双线性变量,φa=xaχa,∀a∈A3;

Ca——增加单位容量所需的费用,∀a∈A2;

da——新加一条路所需的费用,∀a∈A3;

K——新建路段的最大流量;

B——预算投资;

U——足够大的正常数;

3 交通网络设计模型及其鲁棒优化方法

3.1 交通网络设计模型

混合整数线性规划模型是在混合交通网络设计模型的基础上利用分段线性函数法对非线性函数进行线性化.线性化后得到的确定性混合整数线性规划模型[P1]为

式(1)表示目标函数,达到总的出行时间最小.式(2)表示预算约束.式(3)表示满足UE条件的变分不等式约束.式(4)～式(9)表示路段流量、路段容量、旅行时间的范围约束.式(10) ～式(16)表示不修建道路和新建道路的分段线性函数约束.式(17)～式(29)表示扩建道路的分段线性函数的约束.式(30)～式(32)表示双线性项φa= xaχa的线性约束.

3.2 交通网络设计模型的鲁棒优化方法

鲁棒优化考虑的是最坏情况下的最好,它代表一种保守的观点,得到的优化解并不一定是最优的,但是当不确定参数发生扰动时,得到的解仍然是可行的.鲁棒优化方法可以把不确定的系数控制在一个有界区间,从而得到受修建成本扰动较小的鲁棒解.目前,鲁棒凸优化有很大的发展.Goh基于线性决策规则用模块结构对不确定的线性规划问题求近似鲁棒解,文中介绍了隔离不确定性导出新的决策规则的方法[12].Chen通过不对称分布改善不确定集,对变化的约束问题有更好的近似鲁棒解[13].Sim对价格的鲁棒化做了大量的工作,把传统的鲁棒结构转化为线性结构、二次结构、二阶锥结构等,这样的形式转变使得模型求解容易[14]. Janak对混合整数线性规划中确定的参数进行鲁棒优化,由于随机变量符合不同的分布函数,得到不同的不确定模型[15].在交通网络设计问题中,通常情况下,假设修建道路的成本是定值,而忽略了不确定性成本在模型优化方面和可行性方面的影响.然而,由于实际成本和预算成本的不同,最终得到的优化解可能是不可行的,或是不能达到系统性能最优.在文献[5]中,投资价值函数g(ya)用一个简单的线性形式表示,即g(ya)=Caya.但事实上,该函数中的线性系数Ca在实际中普遍存在不确定性.因此,有必要对约束条件式(2)中的投资成本进行鲁棒化.从而得到

式中 ξa2,ξa3,ξB是独立随机变量,ε ＞0是给定的不确定水平.

考虑不等式(33)的可行性,该不等式可以写成下列形式:

根据实值和名义值的关系,式(34)可以写为

可进一步化简为

设随机变量的和为

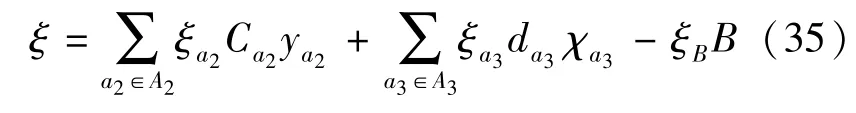
考虑下列形式:

该约束迫使不确定不等式的违反概率至多为k.

定义概率分布函数为

从而生成一个对于给定的不确定水平ε,不可行容限δ,可靠性水平k的基本可行的决定性约束.

通过对问题进行鲁棒化,得到不确定的交通网络模型[P2],即

满足约束条件式(3)～式(32).

4 不同概率分布的不确定交通网络设计模型

上一节在随机变量ξa2,ξa3,ξB的分布函数是未知的情况下进行讨论,为了能得到精确的概率测度,在本节将讨论随机变量满足均匀概率分布和正态概率分布的情况.首先介绍鲁棒解的定义:

命题1(y,x)是一个鲁棒解,若(y,x)满足下列条件:

(1)(y,x)是原始问题的可行解.

(2)不等式(33)的概率测度至多是k,即

4.1 随机变量满足均匀概率分布

假设在成本约束中只有一个不确定的参数,它可以写为

或

或

式中 ξa2,ξa3,ξB是在区间[-1,1]满足均匀分布的随机变量.

定理1给定不确定水平,不可行容限δ和可靠性水平k,随机变量满足均匀分布,不确定的交通网络设计模型[P2]可以写成下列形式:

或

或

满足约束条件式(3)～式(32).其中a2*,a3*表示系数是不确定的道路.

证明设(y,χ)满足下列条件:

若Ca2*是不确定系数,则

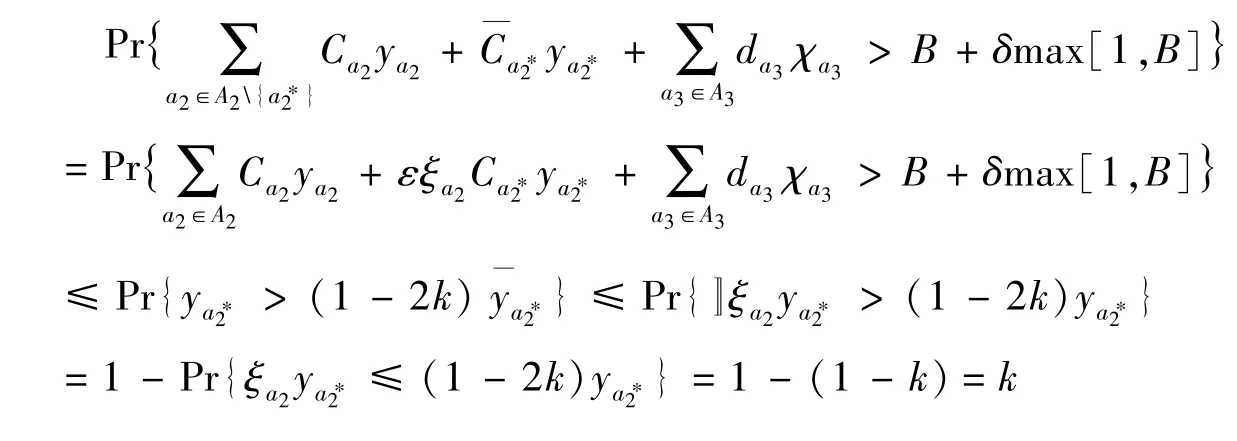
若da3*是不确定系数,则

若B是不确定的常数,则

4.2 随机变量满足正态概率分布

假设随机变量ξa2,ξa3,ξB的分布满足期望为0,标准差为1的标准正态分布,则式(35)中的ξ的分布是期望为0,标准差为的正态分布.记ζ=

定理2给定不确定水平,不可行容限δ和可靠性水平k,随机变量满足期望为0,标准差为ζ的正态分布,则不确定的交通网络设计模型[P2]可以写成下列形式:

满足约束条件式(3)～式(32).

在此λ=F-1

n(1-k),λ和k满足下列关系:

式中 ξ是标准正态分布的随机变量.证明设(y,χ)满足下列条件:

在此λ=Fn-1(1-k),Fn-1是标准正态分布函

[证毕]

数的逆函数,则

[证毕]

由于

也是标准正态分布的随机变量,则最终形成一个混合整数非线性规划问题.

5 算 法

混合整数线性规划问题可由CPLEX12.4有效求解.本文中,有界凸多面体的极点由有限生成算法得到[16].有限生成的混合整数线性规划算法是先通过有限生成算法得到多面体的所有极点,再对混合整数线性规划模型进行松弛,得到松弛混合整 数线性规划模型[P3],即

满足约束条件式(4)～式(32).

求解松弛混合整数线性规划模型的优化解即得混合整数线性规划的优化解.

基于割约束的混合整数线性规划算法(MILPCCA)步骤如下:

第一步 求凸多面体的任意一个极点s,令i =0,X(i)=[x1(i),x2(i),…,xa(i)].

第二步 解混合整数线性规划模型[P3],得到的解为ω(i).

第三步 利用解ω(i),求解公式

第四步 若解ω(i)满足

停止,否则,转到第五步.

第五步对有界多面体Ω的极点进行更新, X(i+1)=X(i)∪*,令i=i+1,转第二步.

6 数值试验

本节通过两个算例对本文所提的算法进行验证.本试验在Inter Core 2 Duo、CPU 2.10 GHz、内存2.00GB PC机上使用 Microsoft Visual Studio 2008和CPLEX 12.4函数库编程实现.

6.1 离散交通网络设计试验

本文以图1中12个结点和一个 (O,D)对 (1,12)组成的网络为基准进行试验.图1表示12个结点的交通网络图,包含12个结点、17条现有路段(实线表示)、6条备选新建路段(虚线表示).已存在道路的自由出行时间由实线上的数字表示,新建道路的自由出行时间由括号中的第一个值表示,新建道路的投资成本值由括号中的第二个值表示,新建道路的标号由括号中第三个值表示.每条路的旅行时间函数表示为tij(xij)=t0ij+0.008x4ij.假设O-D的总需求是20.假设参数的概率分布满足均匀分布,不确定水平 ε=5%,不可行容限δ=20%和可靠性水平k=24%.

图1 12个结点的网络Fig.1 The 12-node network

计算结果如表1所示,它表明随着政府预算投资的增大,用户的旅行时间会变小.在预算投资达到一定的时候,用户的旅行时间会趋于一个定值.由于投资成本的不确定,鲁棒解会趋于定值,最终名义解和鲁棒解达到一致.这说明预算投资足够大时,投资成本对用户旅行时间影响很小.

表1 例1的计算结果Table 1 The results for 12-node network

6.2 连续交通网络设计试验

图2表示由6个结点,8条路段,一个(O,D)对(1,6)组成的交通网络图.道路标号由括号中的第一个值表示,自由出行时间由括号中的第二个值表示,扩建投资成本由括号中的第三个值表示.图中有8条现有路段,假设现需扩建这8条路段,随机变量的概率分布满足均匀分布,不确定水平ε =5%,不可行容限δ=20%和可靠性水平k= 24%.每条路的旅行时间函数表示为 tij(xij)=

从表2中可以看出,政府的投资越多,扩建的道路越多,每条道路的旅行时间越小,这样用户可以降低每条路的旅行时间;同时政府在扩建同一路段时,投资可多可少,这也反映了扩建成本的不确定性.在预算投资不同的情况下,可看出名义解的变化很大,但是鲁棒解却在一定范围内变化,这也说明了鲁棒解更可靠.

图2 6个结点网络道路Fig.2 The 6-node network

表2 例2的计算结果Table 2 The results for 6-node network

7 研究结论

本文考虑了路段修建成本不确定的鲁棒交通网络设计问题,由于交通网络上的路段修建成本存在不确定性,应用鲁棒优化的方法同时考虑出行者的路径选择行为,建立交通网络设计的鲁棒模型.该方法把不确定的系数控制在一个有界的区间,进而得到一个受修建成本扰动较小的鲁棒最优解.由于随机变量满足不同的概率分布,文中分别讨论分析满足均匀分布和正态分布的不确定交通网络设计问题,并运用基于割约束的混合整数线性规划算法对满足均匀分布的不确定交通网络设计模型求解.算例表明,在投资成本不确定的交通网络设计问题中,本文提出的鲁棒优化方法可以得到比传统确定性优化方法更加可靠的解.本文提出的求解算法适用于线性情况,开发针对非线性情况的求解算法将是下一步研究的内容之一.此外,本文只对修建成本不确定的交通网络设计问题进行详细的说明,O-D需求和修建成本同时不确定的交通网络设计问题是今后另外一个重要的研究内容.

[1]Sumalee A.Multi-concentric optimal charging cordon design [J].Transportmetrica,2007,3(1):41-71.

[2]Meng Q,Yang H,Bell M G H.An equivalent continuously differentiable model and a locally convergent algorithm for the continuous network design problem [J]. Transportation Research Part B,2001,35(1): 83-105.

[3]Wang Z W.Global optimum of the linearized network design problem with equilibrium flows [J]. Transportation Research Part B,2010,44:482-492.

[4]Edmunds T A,Bard J F.An algorithm for the mixedinteger nonlinear bilevel programming problem[J]. Annals of Operations Research,1992,34:149-162.

[5]Luathep P.Global optimization method for mixed transportation network design problem: A mixedinteger linear programming approach [J]. Transportation Research Part B,2011,45:808-827.

[6]Yin Y,Lawpongpanich S.A robust approach to continuous network design with demand uncertainty[J]. Transportation and Traffic Theory,2007,17:111-126.

[7]Ordonez F,Zhao J.Robust capacity expansion of network flows[J].Networks,2007,50:136-145.

[8]Mudchanatongsuk S,Ordonez F,Liu J.Robust solutions for network design under cost and demand uncertainty [J]. OperationalResearch Society, 2008, 59: 652-662.

[9]Ban X,Lu S,Ferris M,et al.Risk-averse secondbest toll pricing.Transportation and Traffic Theory. 2009,18:197-218.

[10]Yin Y,Madanat S M,Lu X Y.Robust improvement schemes for road networks under demand uncertainty [J].European Journal of Operational Research, 2009,198(2):470-479.

[11]Lou Y,Yin Y,Lawphongpanich S.A robust approach for discrete network design under demand uncertainty [C].In the proceedings of the 88th Transportation Research Board Meeting,2008.

[12]Goh J,Sim M.Distributionally robust optimization and its tractable approximations [J].Operations Research,2010,58(4):902-917.

[13]Chen M,Alfa A.A network design algorithm using a stochastic incrementaltraffic assignmentapproach [J].Transportation Science,1991,25(3):215-224.

[14]Sim M.Robust optimization[D].PhD thesis, Massachusetts Institute of Technology,2004.

[15]Janak S,Lin X.A new robust optimization approach for scheduling under uncertainty:II.Uncertainty with known probability distribution[J].Computers and Chemical Engineering,2007,31:171-195.

[16]魏权龄,闫洪.广义最优化理论和模型[M].北京:科学出版社,2006.[WEI Q L,YAN H.Generalized optimization theories and models[M].Beijing:Science Press,2006.]

Network Design Problem with Uncertain Construction Costs

XIE Tao-fenga,CHEN Guo-qinga,CAO Jin-xinb
(a.School of Mathematical Sciences,Hohhot 010021,China;b.Department of Transportation Engineering, Inner Mongolia University,Hohhot 010070,China)

The transportation network design problem is an important component of transportation planning theory.With consideration of limited financial resources and travelers'decision-making behavior,it aims to develop the optimal investment strategy.In this paper,a novel network design problem under uncertain construction costs is proposed.Based on the robust optimization method,the budget investment constraints are improved to overcome the limitations of the existing approaches.A global optimization algorithm based on a limited generated method is developed for solving the mixed integer linear programming.A series of comprehensive computational experiments show that in transportation network design problem,the proposed robust optimization method can provide more reliable solutions than the traditional deterministic optimization methods.

urban traffic;uncertain mixed integer linear programming;uncertain investment cost;robust optimization method;transportation network design

U12

A

U12

A

1009-6744(2013)01-0034-09

2012-07-10

2012-09-13录用日期:2012-09-25

国家自然科学基金项目(71061010);内蒙古自治区高等学校科学研究项目(NJ10009);内蒙古大学高层次人才引进科研启动项目(210221).

谢桃枫(1986-),女,内蒙古乌兰察布市人,硕士生.

*通讯作者:cgq@imu.edu.cn