电动汽车充电负荷空间分配优化算法

田文奇 和敬涵 姜久春 牛利勇 王小君

（北京交通大学电气工程学院 北京 100044）

1 引言

面对能源和环境的压力，发展电动汽车，推进低碳型交通，是中国及世界主要发达国家政府关注的热点，各国均加大了对电动汽车的政策扶持力度。可以预计，未来将有大量电动汽车充电负荷接入电网。然而，作为可以移动的负荷，大规模电动汽车在时间和空间上的无序充电行为不仅会出现电力负荷“峰上加峰”的现象，加大电网峰谷差，而且有可能造成电网局部过负荷、线路拥塞等问题，给电网的稳定运行带来影响[1-9]。因此，有必要掌握电动汽车充电的功率需求和能量需求特性，研究在时间和空间两个维度上对电动汽车充电负荷的分配引导方法，研发有序充电控制系统，实现对电动汽车这一移动负荷的优化调度。

在电动汽车充电负荷调度分配和智能充电方法方面，国内外学者已经开展了相关研究。文献[10]以最大化下一时间段所有车辆平均 SOC（state-ofcharge）为目标，采用粒子群算法对电动汽车充电站实时、大规模能量分配进行优化，仿真结果表明算法计算时间适当、受车辆规模影响小，取得了良好效果。文献[11]根据典型交通数据，采用 EDA（estimation of distribution algorithm）算法求解大规模停车场优化能量管理并与其他传统优化算法比较，仿真结果表明EDA算法具有更好的优化效果。文献[12]对工业环境下电动汽车充电设施、电池、智能能量管理、Vehicle-to-Grid、通信设施及需求进行了全面概括和综合介绍，其中对智能能量管理系统及其优化控制算法的总结、展望对本文具有重要的启发意义。文献[13]从负荷、电网损耗和电压等几个方面分析了电动汽车充电对配电网的影响。提出了电动汽车智能充电方法，该方法可在满足电动汽车充电需求的情况下，根据短期负荷趋势，对各时段可充电功率进行优化，达到平稳负荷、降低电能损耗和提高电压质量的目标。文献[14]提出了一种电动汽车有序充电控制方法及系统，根据充电负荷预测结果及电网自身运行情况对充换电站各时刻的允许功率进行合理限制，协调电网负载与电动汽车的能源需求。文献[15]以实时电价为背景，计及供电侧填谷效果与用户成本建立数学模型，并根据模型特点提出了一种基于动态估计插值思想的算法，以达到有效地降低峰谷差，节约用户充电成本，供电侧与用户侧双赢的目标。也有文献以个体电动汽车参与负荷平抑[16]、降低电网损耗[17,19]、减小电压波动[18]、提高负荷系数[19]、节省发电/充电费用[20,21]等为目标，对电动汽车充电时间进行优化。从以上文献可以看出，目前对电动汽车充电负荷的调度优化研究多从时间角度出发，从空间角度对相关问题的优化和求解算法研究较少。本文从空间角度出发，在电动汽车充电负荷空间分配优化问题研究的基础上，通过算例结果对粒子群算法和遗传算法两种优化算法进行对比，分析了两种算法的优化性能。

2 电动汽车充电负荷空间分配优化问题

2.1 问题的假设条件

（1）充电站。某区域电网内接有一定数量的电动汽车充电站和分散充电桩，将位置上相近的分散充电桩看做一个虚拟充电站，与其他充电站共计数量M座。第j个充电站的目标充电功率为Pj。

（2）待充电车辆。区域内共有待充电电动汽车N辆，第i辆电动汽车充电功率Pi取决于充电方式，为变量或恒量。

（3）充电决策变量。xij为决策变量，当 xij=1时，表示第 i辆电动汽车在第 j个充电站充电；当xij=0时，表示第 i辆电动汽车未在第j个充电站充电。 X=为电动汽车充电的决策变量矩阵，行为车辆数量，列为充电站数量，通过对决策变量矩阵X的求解即可得到电动汽车充电负荷空间分配结果。第j个充电站充电的电动汽车数量如式（1）所示，充电功率Pj′如式（2）所示。

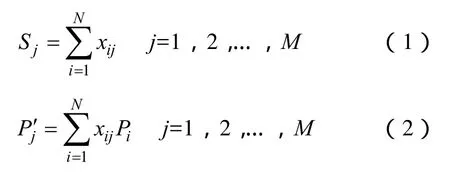
（4）充电路程与时间。第i辆电动汽车到达第j个充电站的路程为lij，电动汽车到充电站的路程矩阵为 L =。第i辆电动汽车到第j个充电站充电的总时间如式（3）所示。

式中，twj为站内排队时间；tcij为充电时间；tdij为到达充电站的行驶时间。twj与选择第j个充电站的车辆数、充电站规模、充电站类型等因素有关，本文近似认为只与充电车辆数成正比，如式（4）所示，kj为比例系数。tcij与充电方式、充电电流倍率有关。tdij与车辆到充电站的路程以及第i辆电动汽车平均行驶速度vi有关，如式（5）所示。

2.2 充电负荷空间分配优化目标函数

为了减小电动汽车充电对电网经济运行的影响，电动汽车充电负荷空间分配优化的目标1是尽量减小各充电站的充电功率与其目标功率之间的差距，如式（6）所示。由于假设充电站目标充电功率以及各车辆充电功率均相同，问题转化为充电车辆数在充电站间的平均分配，如式（7）所示。

式中，Sj为在第 j个充电站充电的电动汽车数量；Sav=N/M为各充电站的平均充电车辆数。

同时，电动汽车充电负荷空间分配优化还要兼顾由于分配造成的充电路程和充电时间增大对电动汽车用户的影响，尽量减小系统内的总充电路程和充电时间。因此如式（8）所示将充电路程和充电时间求和，并以系统内总的充电路程和充电时间最小为目标函数2，如式（9）所示。由于各电动汽车行驶速度、充电时间tcij相同，到达充电站的行驶时间tdij与充电路程 lij成正比，而式（8）中已包含充电路程，因此总充电时间仅考虑站内排队时间twj。

式中，xij为充电决策变量；uij为第 i辆电动汽车到第j个充电站的充电时间和充电路程之和；M为充电站数；N为车辆数。

由于两个目标函数的量纲不同，需要对每个目标函数进行规范化并将多目标优化问题转化为单目标优化问题F，如式（10）所示

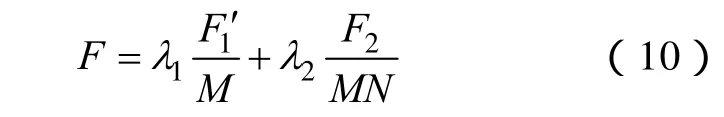
式中，λ1、λ2为目标函数；F1′、F2对应的权系数。

2.3 约束条件

（1）分配约束。每辆电动汽车能且仅能分配至一个充电站充电。

（2）充电路程约束。由于车辆剩余电量不足、交通堵塞或无可达路径、电动汽车用户主观意愿造成的可分配的充电路程最大值limax。

3 充电负荷空间分配优化算法

充电负荷空间分配优化问题是一个非连续、多变量、非线性、高维的优化问题，基于梯度的传统优化方法难以解决，而基于概率搜索的具有随机性与导向性相结合特点的智能优化方法在求解这一类问题时具有一定优势，因此本文采用应用较为广泛、成熟的粒子群算法和遗传算法对比求解并分析其效果。

3.1 粒子群优化算法

粒子群优化算法(PSO)是 Eberhart和 Kennedy提出的模拟鸟群飞行觅食行为的算法，通过鸟之间的集体协作使群体达到最优。该算法通过式（13）、式（14）迭代更新粒子的位置和速度，其详细含义可参考文献[22]，本文不再熬述。

式中，w为惯性权重；c1、c2是学习因子，通常取c1、c2=2；rand1、rand2是[0,1]之间的随机数。

3.1.1 粒子位置设置

使用PSO算法优化充电负荷的空间分配时，将每辆车在每个充电站的充电决策变量 xij作为粒子的位置坐标，如式（15）所示，粒子维数为N×M。

3.1.2 约束条件处理

（1）分配约束。由于标准粒子群算法是针对连续解空间的优化，而充电负荷空间分配问题的解空间是离散的二进制空间，要满足其约束条件以及计算目标函数需要将连续空间转换为离散空间。对于式（15）所示的随机迭代生成的粒子位置坐标，取每辆车位置坐标最大值对应的维作为决策变量取 1的维，其他维取 0。如此即可以满足分配约束，又可以用转换后的离散解空间计算各粒子的目标函数并比较、记录。

（2）充电路程约束。充电路程约束是一个不等式约束，可以采用类似罚函数法的思想，对于路程矩阵L中大于limax的元素，将其改为一个足够大的正数。当其对应的车与站被配对时，会使适应度值显著增大，从而起到对约束条件被破坏的惩罚作用。

3.1.3 算法流程

粒子群算法求解电动汽车充电负荷空间分配优化问题的流程图如图1所示。

图1 粒子群算法流程图Fig.1 PSO flow chart

3.2 遗传算法

遗传算法（GA）是由美国教授J.Holland于1975年首先提出来的模拟达尔文生物进化论自然选择和遗传学中生物进化过程的随机化搜索方法。它将问题的解编码成染色体，通过遗传算子选择、交叉、变异来产生新一代更适应环境的染色体，不断繁殖、进化并最终达到最优解。

3.2.1 遗传操作

（1）选择算子。选择是从种群中选择适应度高的染色体产生新种群的过程。通常染色体适应度越高，被选中的概率越大，其子孙在下一代中的个数越多。为保持种群的多样性，本文采用全选的方法，即所有染色体的选择概率均为1。

（2）交叉算子。当许多染色体的适应度相同时，可以通过交叉算子来产生新一代染色体，交叉算子是产生新个体的主要手段。本文采用均匀交叉方法，将每个点都作为潜在的交叉点，随机地产生与个体等长的 0-1掩码，掩码中的片段表明了哪个父个体向子个体提供变量值。

（3）变异算子。变异是以一定的概率随机改变某些个体的某些基因位的值，从而获得新的个体。为避免早熟以及收敛速度慢的问题，本文采用改进的自适应变异方法[23]，通过式（16）来确定变异概率。

式中，pm表示个体变异概率；pm1表示最大变异概率；pm2表示最小变异概率；f表示要变异个体的适应度值；favg表示种群平均适应度值；fmax表示种群中的最大个体适应度。

3.2.2 约束条件处理（编码）

（1）分配约束。虽然二进制编码是遗传算法应用最广泛的编码方式之一，但由于要满足分配约束条件，本文采用 1～M之间的整数编码形式完成遗传操作，仅在计算适应度函数时将整数编码转换为决策变量的 0-1编码。因此，本算法的维数为 N，远小于粒子群算法的维数。

（2）充电路程约束。充电路程约束的处理方法同粒子群算法。

3.2.3 算法流程

遗传算法求解电动汽车充电负荷空间分配优化问题的流程图如图2所示。

图2 遗传算法流程图Fig.2 GA flow chart

4 算例仿真

4.1 算例数据

假设区域内共接入充电站 M=5座，电动汽车N=50辆，充电路程 lij在数千米到十几千米之间随机生成。文献[24]中指出电动汽车充电站服务半径为数千米，取可分配的充电路程最大值limax=10km，超出约束条件的取足够大正数1000代替，见表1。排队时间与充电车辆数比例系数 kj=2,1,3,2,1( j = 1,2 … ,M )，目标函数权系数λ1=0.6、λ2=0.4。粒子群算法中取粒子数为 100，最大迭代次数为 500，惯性权重在0.4～0.9之间线性递减。遗传算法中取群体数为100，最大迭代次数为500，pm1=0.1，pm2=0.01。

4.2 算例结果

经过迭代计算得到区域内所有车辆在各充电站间的分配结果，即决策变量矩阵X见表2和表3。其中 PSO算法得到的目标函数 F1=0、F2=1091、F=1.7456，GA算法得到的目标函数 F1=0、F2=1025、F=1.64。同时，所有车辆仅被分配至一个充电站，且超出路程约束的车辆和充电站均未被分配，满足约束条件。结果表明所有充电车辆被平均分配至各充电站的同时，尽量减小了系统内的总充电时间和充电路程，验证了两种算法的有效性和可行性。

表1 电动汽车到各充电站之间的路程Tab.1 The distances between EVs and charging stations

表2 PSO充电负荷空间分配结果（决策变量矩阵X）Tab.2 The result of charging load spatial dispatching by PSO（decision variables matrix X）

表3 GA充电负荷空间分配结果（决策变量矩阵X）Tab.3 The result of charging load spatial dispatching by GA（decision variables matrix X）

4.3 算法性能分析

电动汽车充电负荷空间分配优化问题是一个高维优化问题，优化算法在高维数时的计算速度决定了控制系统的实时性。图3、表4给出了两种算法在不同车辆数和充电站数时的收敛曲线、计算时间和适应度。结果表明，遗传算法在各种情况下的收敛速度、适应度计算结果均优于粒子群算法，且在高维时更明显，因此遗传算法具有较高的实用性。

图3 算法收敛曲线比较Fig.3 The comparison of convergence tendency

表4 算法计算结果比较Tab.4 The comparison of calculation results

5 结论

本文以充电负荷均匀分配和系统内充电路程、时间最小为目标研究了电动汽车充电负荷的空间分配优化问题，采用粒子群算法和遗传算法分别对问题进行优化求解。最后，仿真算例验证了两种优化方法的有效性和实用性，并通过算例分析了两种优化算法的性能，结果表明遗传算法在电动汽车充电负荷的空间分配优化中的性能优于粒子群算法。需要指出的是，本文仅采用单目标优化算法中的标准粒子群算法和遗传算法进行比较，并未涉及其他改进算法和多目标优化算法，其性能分析和改进提高还有很大空间，有待进一步研究。

[1]高赐威, 张亮.电动汽车充电对电网影响的综述[J].电网技术,2011, 35(2): 127-131.Gao Ciwei, Zhang Liang.A survey of influence of electrics vehicle charging on power grid[J].Power System Technology,2011, 35(2): 127-131.

[2]赵俊华, 文福拴, 杨爱民, 等.电动汽车对电力系统的影响及其调度与控制问题[J].电力系统自动化,2011, 35(14): 2-10.Zhao Junhua, Wen Fushuan, Yang Aimin, et al.Impacts of electric vehicles on power systems as well as the associated disp atching and control problem[J].Automation of Electric Power Systems,2011, 35(14):2-10.

[3]王辉, 文福拴, 辛建波.电动汽车充放电特性及其对配电系统的影响分析[J].华北电力大学学报,2011, 38(5): 17-24.Wang Hui, Wen Fushuan, Xin Jianbo.Charging and discharging characteristics of electric vehicles as well as their impacts on distribution systems[J].Journal of North China Electric Power University,2011, 38(5):17-24.

[4]Kristien Clement Nyns, Edwin Haesen, Johan Driesen.The impact of vehicle-to-grid on the distribution grid[J].Electric Power Systems Research,2011, 81(1):185-19 2.

[5]Michael Caramanis, Justin M.Foster.Management of electric vehicle charging to mitigate renewable generation intermittency and distribution network congestion[C].Proceedings of the 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference,2009: 4717-472 2.

[6]Qian Kejun, Zhou Chengke, Malcolm Allan, et al.Load model for prediction of electric vehicle charging demand[C].Proceedings of the 2010 International Conference on Power System Technology,2010: 1-6.

[7]Saker N, Petit M, Vannier J C.Electric vehicles charging scenarios associated to direct load control programs(DLC)[C].Proceedings of the North American Power Symposium(NAPS),2011: 1-7.

[8]Rowand M.The electricity utility-business case[C].Plug-In Conference, San Jose CA: EPRI, Silcon Valley Leadership Group,2009.

[9]Lopes J A P, Soares F J, Almeida P M R.Integration of electric vehicles in the electric power system[J].Proceedings of the IEEE,2011, 99(1): 168-18 3.

[10]Su W, Chow M Y.Performance evaluation of a PHEV parking station using particle swarm optimization[C].Proceedings of IEEE Power and Energy Society General Meeting,2011: 1-6.

[11]Su W, Chow M Y.Performance evaluation of an EDA-based large-scale plug-in hybrid electric vehicle charging algorithm[J].IEEE Transactions on Smart Grid,2012, 3(1): 308-315.

[12]Su W, Rahimi H Eichi, Zeng W, et al.Chow.A survey on the electrification of transportation in a smart grid environment[J].IEEE Transactions Industrial Informatics,2012, 8(1): 1-10.

[13]李惠玲, 白晓民.电动汽车充电对配电网的影响及对策[J].电力系统自动化,2011, 35(17): 38-4 3.Li Huiling, Bai Xiaomin.Impacts of electric vehicles charging on distribution grid[J].Automation of Electric Power Systems,2011, 35(17): 38-4 3.

[14]中国电力科学研究院.电动汽车有序充电控制方法及系统: 中国, CN102055217A[P].2011-05-11.

[15]邹文, 吴福保, 刘志宏.实时电价下插电式混合动力汽车智能集中充电策略[J].电力系统自动化,2011, 35(14): 62-67.Zou Wen, Wu Fubao, Liu Zhihong.Centralized charging strategies of plug-in hybrid electric vehicles under electricity markets based on spot pricing[J].Automation of Electric Power Systems,2011, 35(14):62-67.

[16]韩海英, 和敬涵, 王小君, 等.基于改进粒子群算法的电动车参与负荷平抑策略研究[J].电网技术,2011, 35(10): 165-169.Han Haiying, He Jinghan, Wang Xiaojun, et al.Strategy research of v2g participating load responses based on improved particle swarm optimization[J].Power System Technology,2011, 35(10): 165-169.

[17]Kristien Clement Nyns, Edwin Haesen, Johan Driesen.The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J].IEEE Transactions on Power Systems,2010,25(1):371-380.

[18]Sara Deilami, Amir S Masoum, Paul S Moses, et al.Real-time coordination of plug-in electric vehicle charging in smart grids to minimize power losses and improve voltage profile[J].IEEE Transactions on Smart Grid,2011,2(3): 456-466.

[19]Eric Sortomme, Mohammad M Hindi, James MacPherson S D, et al.Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system Losses[J].IEEE Transactions on Smart Grid,2011,2(1): 198-205.

[20]Somayeh Sojoudi, Steven H Low.Optimal charging of plug-in hybrid electric vehicles in smart grids[C].Proceedings of the IEEE Power & Energy Society General Meeting,2011: 1-6.

[21]Niklas Rotering, Marija Ilic.Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets[J].IEEE Transactions on Power Systems,2011,26(3): 1021-1029.

[22]纪震, 廖惠连, 吴青华.粒子群算法及应用[M].北京: 科学出版社,2009.

[23]任子武, 伞冶.自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报,2006, 18(1):41-4 3.Ren Ziwu, San Ye.Improved adaptive genetic algorithm and its application research in parameter identification[J].Journal of System Simulation,2006,18(1): 41-4 3.

[24]刘志鹏, 文福拴, 薛禹胜, 等.电动汽车充电站的最优选址和定容[J].电力系统自动化,2012, 36(3):54-59.Liu Zhipeng, Wen Fushuan, Xue Yusheng, et al.Optimal siting and sizing of electric vehicle charging stations[J].Automation of Electric Power Systems,2012, 36(3): 54-59.