微电网系统中基于双二阶滤波器的主动阻尼方法
2013-08-07陆晓楠黄立培
陆晓楠 孙 凯 黄立培
(清华大学电力系统及大型发电设备安全控制和仿真国家重点实验室 北京 100084)
1 引言
传统的化石燃料由于储量有限,且在使用的过程中会对环境造成污染,已经无法满足人们日益增长的能源需求。与此同时,各类可再生能源由于具有储量丰富、清洁无污染等多方面的优点,得到了工业界和学术界的不断关注[1,2]。随着可再生能源在现代电力系统中所占比例的不断提升,学者们提出了微电网的概念,以实现对区域内可再生能源的整合,使其对内满足负荷功率在不同分布式电源之间的合理分配,对外形成电能可控单元,实现和外部大电网之间的能量交换[3,4]。为了提升本地供电质量,并满足并网标准要求,在微电网系统中,通常需要以电力电子变换器作为接口实现各类可再生能源的接入[5,6]。由于微电网中可再生能源具有分布式接入特点,各电力电子接口变换器之间大多满足并联关系[7-9]。
电力电子接口变换器通常采用脉冲宽度调制(Pulse Width Modulation,PWM)方式,因此在输出波形中存在开关频率整数倍附近的高频谐波。为了实现对高频谐波的有效抑制,通常采用LCL形式的交流侧输出滤波器。LCL滤波器在低频段接近于单电感滤波器,满足对工频分量的低通特性;而在高频段较单电感滤波器具有较大的抑制率,可以实现对高频分量的有效抑制。和单电感滤波器相比,LCL滤波器可以利用取值较小的储能元件实现单电感滤波器的滤波效果,功率密度更大,且对外干扰较小,因此在工程中得到了广泛使用。尽管LCL滤波器具有多方面的优点,其频谱中存在着固有的谐振尖峰。如果参数设计不当,来自内部或外部的扰动会在系统中激发起较为严重的谐振,影响系统的稳定运行[10,11]。
为了解决LCL滤波器的谐振问题,学者们提出了多种方法。概括来讲,LCL谐振抑制方法可以分为被动方法和主动方法两类[12]。通过在滤波器电容支路串联电阻,可以简单地通过被动阻尼方法抑制谐振问题。该方法的抑制效果明显,但由于引入了电阻,造成了额外的功率消耗,系统效率有所下降。主动阻尼方法通过改变控制结构实现阻尼效果,不需要在滤波器中实际接入电阻,因此避免了额外的系统损耗,有较为广泛的应用。主动阻尼可以通过多环控制和引入阻尼滤波器两类方法实现。在多环控制实现方法中,需要增加传感器,对额外的变量进行测量,并引入新的控制闭环,以对频域内谐振尖峰进行抑制。在阻尼滤波器实现方法中,无需增加额外的传感器,系统成本有所降低,通过引入新的零极点,改变原有系统闭环极点的分布,使其调整到稳定区域内。
对于 LCL滤波器谐振问题的分析往往集中在单逆变器系统中,而随着新能源输入端的不断接入,传统的分析方法并不能彻底解决系统中的谐振问题,其原因在于大量逆变器同时存在造成多个LCL滤波器并联接入公共母线。由于具有多个无源元件,系统的频域特性有所改变,不同于传统的单逆变器系统只存在唯一一个谐振尖峰的特点[13,14]。因此,相应的谐振抑制方式也需要同样做出调整,以适应更为复杂的系统谐振情况。
本文在考虑微电网中并联逆变器系统 LCL滤波器谐振分布的基础上,对基于双二阶滤波器的主动阻尼方法进行扩展,以同时对多个谐振尖峰进行抑制,满足系统稳定运行的要求。
2 并联逆变器系统谐振特性分析
微电网中并联逆变器系统典型结构如图 1所示。从图中可以看出,各可再生能源输入端通过带有 LCL滤波器的电力电子接口变换器接入公共母线,各变换器之间呈现并联关系。为了分析由LCL滤波器引入的谐振尖峰,可以将图1的交流侧进行简化,如图2所示。此处选择控制滤波器网侧电感电流,而直流电源及逆变器以电压源形式简化表示。图2中Z1k和Z2k分别为滤波器逆变器侧和网侧电感阻抗,Zck表示滤波电容支路阻抗,Zg表示网侧等效阻抗。其中,k=1,2,…,n。

图1 微电网中并联逆变器系统典型结构Fig.1 Typical configuration of the parallel inverter system in a microgrid

图2 并联逆变器系统交流侧简化模型Fig.2 AC side simplified model of the parallel inverter system
系统控制结构可用式(1)和式(2)表示。

式中,Igi(i=1,2, …,n)表示网侧电感电流;Ui(i=1,2,…,n)表示逆变器输出电压;Ug表示电网电压;Gf表示网侧电流到逆变器输出电压的传递函数矩阵;Gg表示网侧电流到电网电压的传递函数矩阵。
系统谐振情况可以通过对系数矩阵 Gf和 Gg的分析得到。为了表述方便,首先设定

各并联逆变器组成线性系统,因此为了得到传递函数 Gfii、Gfij、Ggi(i,j=1,2,…,n),可以分别将逆变器交流侧LCL滤波器网络简化为图3a、图3b和图3c所示的结构。
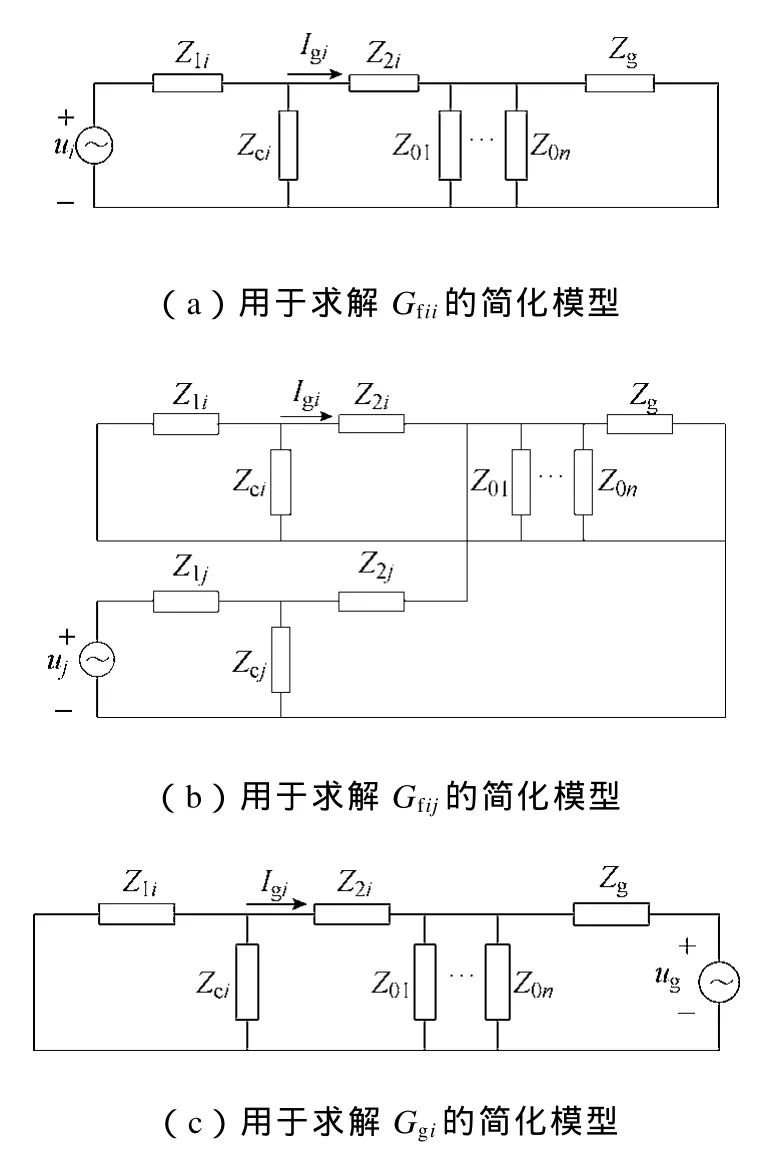
图3 LCL滤波器网络简化模型Fig.3 Simplified model of the LCL filter network
假定

求解图3中各等效电路,可得
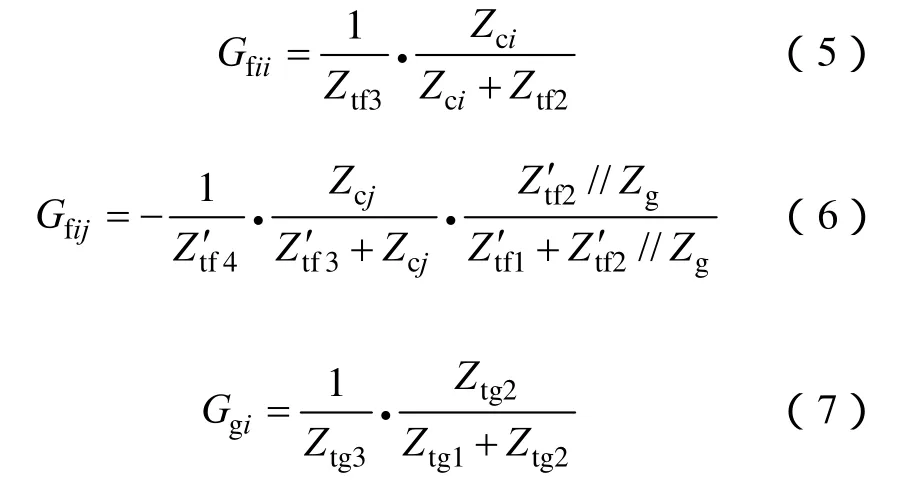
以 Gf11,Gf12和 Gg1,即 u1到 ig1,u1到 ig2和 ug到ig1的传递函数为例,采用表1所示的参数,得到的频域分析结果如图 4所示。和传统的单个带有LCL滤波器的逆变器相比,系数矩阵Gf体现出的谐振尖峰不只一个,Gf11和 Gf12的频谱中出现了额外的正向谐振尖峰和反向谐振尖峰。随着并联逆变器个数的增加,频率较高的正向谐振尖峰的位置保持不变,而频率较低的谐振尖峰向低频段移动。同时,系数矩阵 Gg体现出单正向谐振尖峰和单反向谐振尖峰的频谱特点。随着并联逆变器个数的增加,处于较低频率的反向谐振尖峰的位置保持不变,而处于较高频率的正向谐振尖峰的位置向低频段移动。

表1 并联逆变器系统参数Tab.1 Parameters of the parallel inverter system
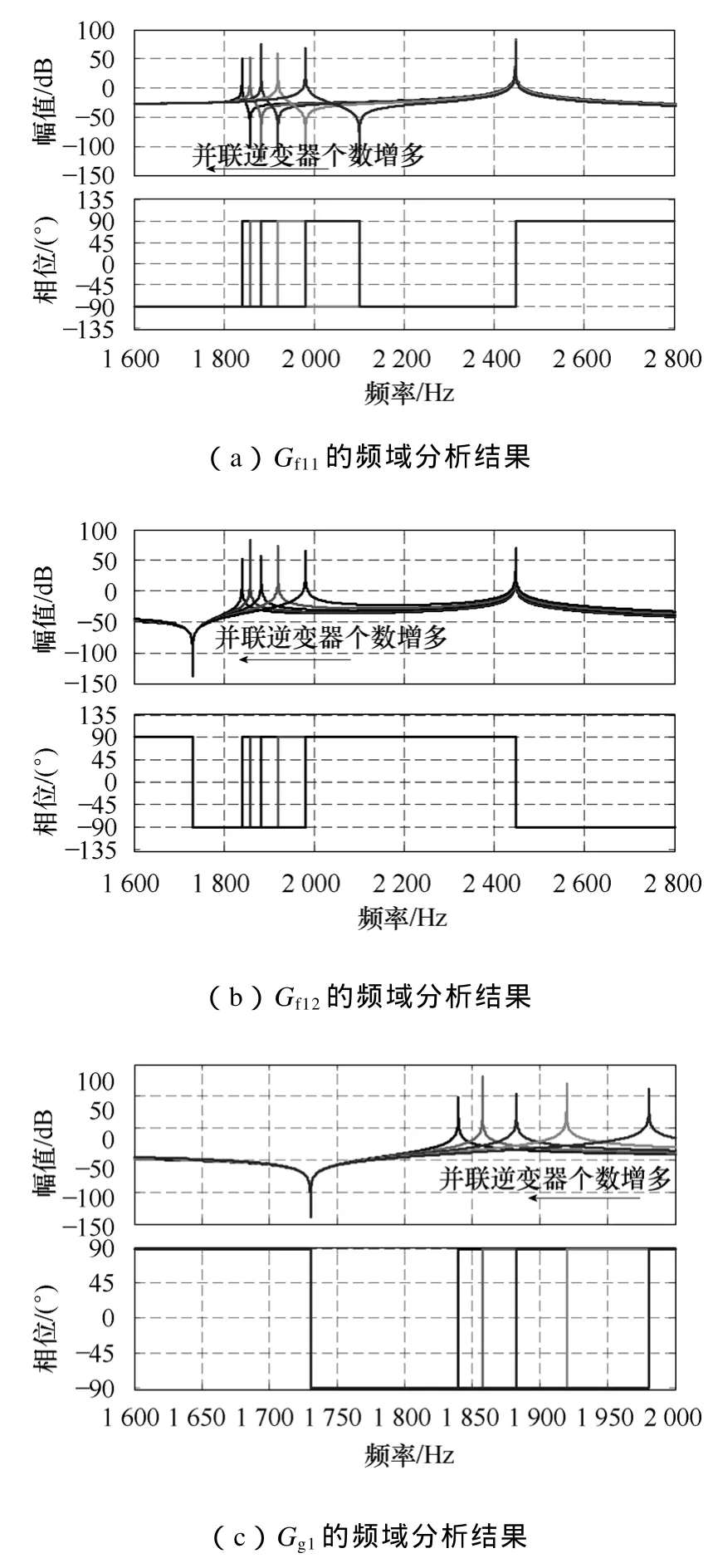
图4 并联逆变器系统谐振分析结果Fig.4 Frequency domain analysis results of the parallel inverter system
3 基于双二阶滤波器的并联逆变器谐振抑制方法
为了对微电网中并联逆变器系统的谐振问题进行抑制,本文在不增加额外的传感器以及控制闭环的情况下,采用基于双二阶滤波器的主动阻尼方法,通过引入两对零极点,使得闭环系统中所有的主导极点均位于z平面单位圆之内,以满足系统稳定性要求。
具体来讲,并联逆变器系统的控制结构如图 5所示。从图中可看出,并联逆变器系统可以看做一个多输入多输出(Multi-Input-Multi-Output,MIMO)系统,其中用于主动阻尼的双二阶滤波器结构为
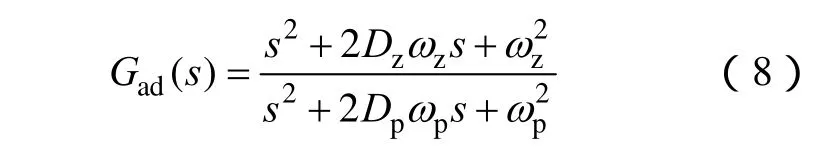
对式(8)进行双线性离散化,设定


图5 并联逆变器系统控制结构Fig.5 Control diagram of the parallel inverter system
将式(9)代入式(8),可得

双二阶滤波器在z域平面内的零极点分布如图6所示,滤波器参数取值见表2。采用双二阶滤波器之后,在原有控制结构中引入了两对额外的零极点,因此改变了根轨迹的走向,使得不稳定的闭环极点位置迁移到z平面单位圆之内,满足稳定性要求。

表2 双二阶滤波器参数Tab.2 Parameters of the bi-quad filter
以控制系统中逆变器#1网侧电流到其电流给定值的传递函数为例,检验基于双二阶滤波器的主动阻尼作用效果。在并联逆变器系统中,若未使用基于双二阶滤波器主动阻尼方式,系统的零极点分布如图7所示。从图中可以看出,影响系统稳定性的极点为图中放大区域内的两对极点。当采用基于双二阶滤波器的主动阻尼方法后,在z平面内引入图6所示的两对零极点。由于引入了新的零极点,开环系统根轨迹走向发生改变,从而改变了闭环极点在z平面的分布。如图8所示,加入双二阶滤波器后,原有影响系统稳定性的两对极点均移动到单位圆之内,因此系统稳定性得以保证。需要注意的是,闭环系统中其他的极点由于和零点抵消,因此未在此处加以考虑。

图6 双二阶滤波器在z域平面内的零极点分布Fig.6 Positions of zeross and poles of bi-quad filter in z domain
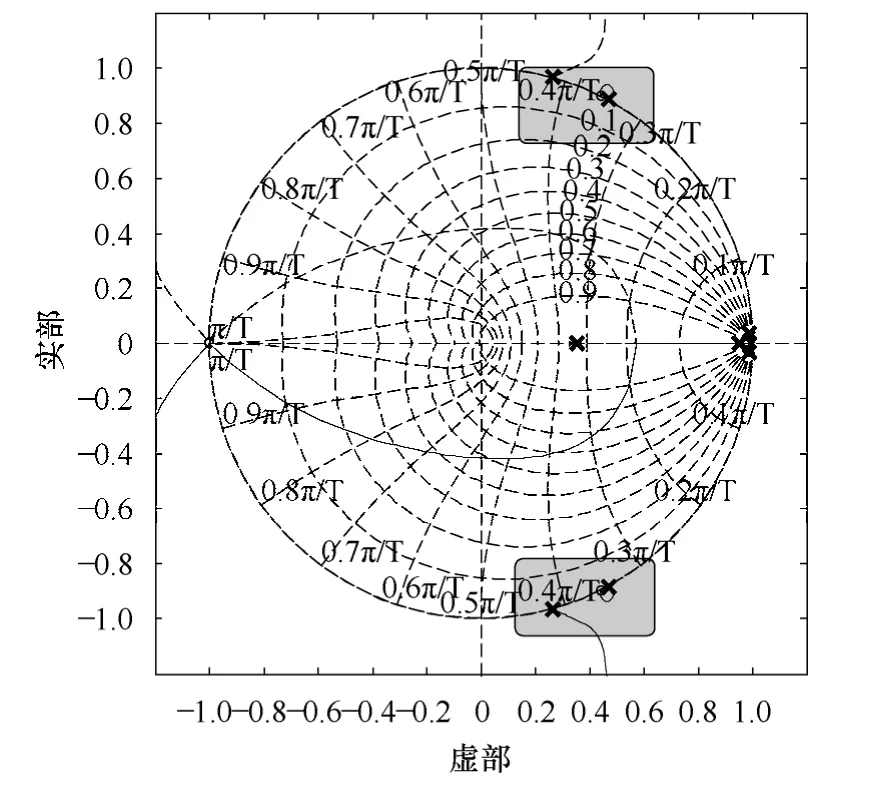
图7 未使用基于双二阶滤波器的主动阻尼方式情况下的系统零极点分布Fig.7 Positions of zeros and poles without active damping method
4 基于dSPACE的实时仿真

图8 使用基于双二阶滤波器的主动阻尼方式情况下的系统零极点分布Fig.8 Positions of zeros and poles with bi-quad based active damping method
为了对上述并联逆变器系统中基于双二阶滤波器的主动阻尼方法进行验证,以3台带LCL滤波器的并联逆变器系统为例,建立了基于 dSPACE1103的实时仿真模型,其结构如图9所示。系统模型参数见表1。

图9 带有3台并联逆变器的实时仿真模型Fig.9 Real-time simulation model of three LCL-filtered parallel inverters
首先,验证主动阻尼开启和停止的暂态响应结果。以逆变器#1的α和β轴并网电流波形为例,如图10所示,在t=0时刻开启主动阻尼。在t=0时刻之前,系统处于严重的谐振状态;而在开启基于双二阶滤波器的主动阻尼之后,系统逐渐趋于稳定,波形恢复为理想的正弦状态。如图11所示,在t=0时刻关断主动阻尼,图中仍为第一台逆变器的α轴和β轴并网电流波形。在t =0时刻之前,并网电流波形处于正常正弦状态;而在关断主动阻尼之后,系统发生严重的谐振问题,进入不稳定状态。
之后,验证上述主动阻尼方法对并网电流给定值跳变的适应性。在确保主动阻尼开启的情况下,设置并网电流幅值给定在t=0时刻从2A跳变为3A,以第一台逆变器为例,得到的电流波形如图 12所示。从图中可以看出,基于双二阶滤波器的主动阻尼方法在电流给定值跳变情况下具有良好的谐振抑制效果。

图10 主动阻尼开启时刻逆变器#1的暂态波形Fig.10 Transient waveforms of inverter #1 when active damping is turned on


图11 主动阻尼关断时刻逆变器#1的暂态波形Fig.11 Transient waveforms of inverter #1 when active damping is turned off

图12 给定值跳变时刻逆变器#1的暂态波形Fig.12 Transient waveforms of inverter #1 with step reference
最后,验证上述主动阻尼方法对网侧扰动的适应性。在确保主动阻尼开启的情况下,设置并网电流给定值为 3A且保持不变。同时,电网电压幅值在t=0时刻从230V跳变为250V。同样以第一台逆变器为例,网侧电压以及并网电流的α轴和β轴分量如图13所示。从图中可以看出,基于双二阶滤波器的主动阻尼方法在网侧扰动情况下具有良好的谐振抑制效果。

图13 网侧电压扰动时刻逆变器#1的暂态波形Fig.13 Transient waveforms of inverter #1 with grid voltage disturbance
5 结论
本文针对微电网系统中并联逆变器谐振特点,研究了基于双二阶滤波器的主动阻尼方法,得到以下结论:
(1)和传统的单逆变器系统相比,微电网并联逆变器系统中存在多个谐振尖峰,对系统稳定性具有更大的影响。
(2)采用基于双二阶滤波器的主动阻尼方法在不引入额外的传感器及控制环的情况下,在控制系统中添加两对零极点,可以改变根轨迹走向,进而调整闭环极点位置,使得影响系统稳定性的极点移动到z平面单位圆之内,同时实现对并联逆变器系统多谐振尖峰的抑制。
(3)上述基于双二阶滤波器的主动阻尼方法在电流给定值跳变以及网侧电压扰动的情况下具有良好的谐振抑制效果。
[1]王飞, 余世杰, 苏建徽, 等.太阳能光伏并网发电系统的研究[J].电工技术学报,2005,20(5): 72-74,91.Wang Fei, Yu Shijie, Su Jianhui, et al.Research on Photovoltaic grid-connected power system[J].Transactions of China Electrotechnical Society,2005,20(5): 72-74, 91.
[2]刘其辉, 贺益康, 赵仁德.交流励磁变速恒频风力发电系统的运行与控制[J].电工技术学报,2008,23(1): 129-136.Liu Qihui, He Yikang, Zhao Rende.Operation and control of AC-exited variable-speed constantfrequency wind power generation system [J].Transactions of China Electrotechnical Society,2008,23(1): 129-136.
[3]Lasseter R, Akhil A, C Marnay, et al.The certs microgrid concept-white paper on integration of distributed energy resources [R].Technical Report,U.S.Department of Energy, April,200 2.
[4]Chris Marnay, Owen C Bailey.The CERTS microgrid and the future of the macrogrid [C].ACEEE Summer Study on Energy Efficiency in Buildings,2004.
[5]Blaabjerg F, Chen Z, Kjaer S B.Power electronics as efficient interface in dispersed power generation systems[J].IEEE Transactions on Power Electronics,2004, 19(5): 1184-1194.
[6]Carrasco J M, Franquelo L G, Bialasiewicz J T, et al.Power-electronic systems for the grid integration of renewable energy sources: a survey[J].IEEE Transactions on Industry Electronics,2006, 53(4):1002-1016.
[7]沈坤,章兢,王坚.基于PQ下垂控制逆变器并联技术的列车辅助供电系统研究[J].电工技术学报,2011,26(7):223-229.Shen Kun, Zhang Jing, Wang Jian.Research on train auxiliary power system based on PQ droop control inverter parallel technology[J].Transactions of China Electrotechnical Society,2011,26(7): 223-229.
[8]张纯江, 王晓寰, 薛海芬, 等.微网中三相逆变器类功率下垂控制和并联系统小信号建模与分析[J].电工技术学报,2012,27(1): 32-39.Zhang Chunjiang, Wang Xiaohuan, Xue Haifen, et al.a quasi-power droop control of three-phase inverters and small signal modeling and analysis of parallel system in micro-grid[J].Transactions of China Electrotechnical Society,2012,27(1): 32-39.
[9]Guerrero J M, Hang L, Uceda J.Control of distributed uninterruptible power supply systems[J].IEEE Transactions on Industry Electronics,2008,55(8):2845-2859.
[10]Liserre M, Blaabjerg F, Hansen S.Design and control of an LCL-filter-based three-phase active rectifier [J].Transactions on Industry Applications,2005,41(5):1281-1291.
[11]Liserre M, Aquila A D, Blaabjerg F.Genetic algorithm-based design of the active damping for an LCL-filter three-phase active rectifier[J].IEEE Transactions on Power Electronics,2004, 19(1):76-86.
[12]Teodorescu R, Liserre M, Rodriguez P.Grid convertersfor photovoltaic and wind power systems [M].Wiley,2011.
[13]Agorreta J L, Borrega M, Lopez J, Marroyo L.Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J].IEEE Transactions on Power Electronics,2011,26(3): 770-785.
[14]He J, Li Y W, Bosnjak D, et al.Investigation and active damping of multiple resonances in a parallelinverter-based microgrid[J].IEEE Transactions on Power Electronics,2013,28(1): 234-246.
