水平裂隙发育储层垂直井声波测井响应研究

许孝凯 ，刘美杰 ，孙超囡 ，熊 宇，周朋飞

（1.中国石油大学 地球科学与技术学院，山东 青岛 266555；2.中国石油大学 CNPC测井重点实验室，山东 青岛 266555；3.胜利石油管理局 测井公司，山东 东营 257096；4.大港油田勘探开发研究院，天津 300280；5.川庆钻探工程公司 测井公司，重庆 400021）

0 前言

由于沉积压实、构造应力、地球化学等作用，地壳岩石中普遍发育微裂隙［2］，地下裂隙不但可以成为油气运移的通道，本身也是油气聚集的场所，它在寻找油气、天然气水合物资源等有着重要的意义。据估计，由于地下裂隙、溶洞的存在，油气田在首次开发之后，仍有70%～80%的油气资源尚未开发出来。因此，裂隙性储层的研究不但是石油地质学家及油藏工程师感兴趣的问题，近年来也引起了勘探地球物理学家们的重视［1］。

裂隙介质的研究从上个世纪八十年代就由Crampin［2］开展，并指出裂隙诱导的各向异性有可能是弹性波各向异性的主要成因，同时提出了广泛扩容各向异性介质模型即EDA 介质。随后，人们对裂隙发育的岩石物理模型和地球物理勘探模型进行了一系列的探索。较早的研究是针对含定向裂隙介质有效弹性模量展开的［3］，但是该模型仅仅适用于孤立裂隙，且二阶展开不是一个单一的收敛序列。针对二阶展开不是单一收敛序列的问题，Cheng［4］提出了改进的Eshelby－Cheng各向异性裂隙介质模型。一个重要的模型是对Hudson模型的推广，使得其适用于连通裂隙的模型［5］，但该理论是对各向同性介质的模型。一种利用线性滑动理论建立的新的裂隙岩石物理模型［6］，该理论不受裂隙形状和微结构的限制，具有较好的适用性，但该模型无法考虑裂缝产生的孔隙度和渗透率影响。作者在考虑裂隙内流体因素影响中，引入喷射流机制，即将孔隙分成软性和刚性孔隙［7］，也取得了较好的效果。在随后的工作中，该模型也被成功应用于井孔声场模拟［8］。但模拟不同裂隙参数下的声波测井响应，并分析裂隙参数对声波响应影响的还很少。

作者在Eshelby－Cheng模型的基础上，应用实轴积分方法，研究了水平分布的裂隙介质（VTI）声波测井响应波形及频散分析，给出了弹性参数计算公式，并分析了裂隙介质与各向异性之间的内在联系。

1 水平裂隙发育储层声波测井模型

1.1 裂隙介质的Eshelby－Cheng模型［9］

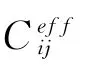
其中 各参数表达式及定义见岩石物理手册［9］。

与Hudson模型不同，这个模型对任意高宽比都适用。

1.2 横向各向同性介质声波测井模拟

理论全波波形及频散曲线的计算步骤，见定量测井声学［10］：

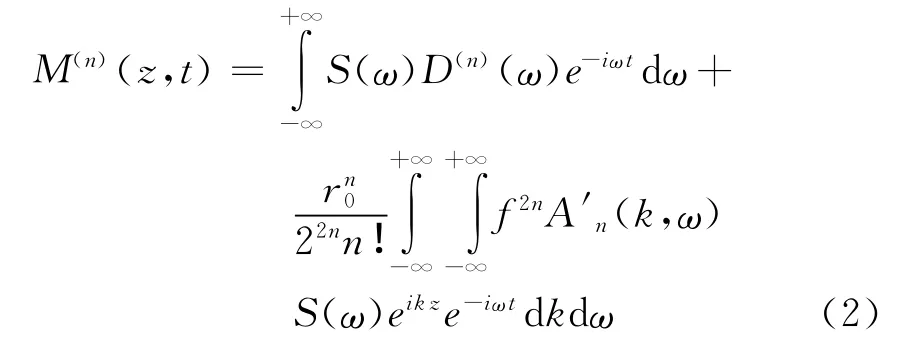
其中D（n）（ω）是声源辐射贡献；S（ω）是源的频谱，其函数形式可以任意选取。

为了模拟方便选取中心频率为ω0的瑞克子波，S（ω）和D（n）（ω）的表达式如式（3）所示：

某振型的激发函数为：

其中 波数kl是波数k在第l个极点处的取值；矩阵Qij为Q的代数余子式，是把矩阵Q去掉第i行第j列得到的，矩阵Q表达式见定量测井声学［10］。

在分析因素影响时，常用到灵敏度分析，模型对某参数p的灵敏度定义如下：

其中vphase（ω）为模式波的相速度。

将1.1节中利用裂隙参数得到的等效弹性模量参数，带入到1.2节横向各向同性声波测井模拟中，便可数值模拟水平裂缝发育储层声波测井全波波形及频散曲线。

2 数值模拟结果及分析

作者建立了垂直井条件下水平裂隙的发育模型，即VTI地层，如下页图1所示。

单个裂隙如下页图2所示。

采用表1参数（见下页），对裂隙发育储层的单极和偶极波形进行模拟，其中vps为骨架的纵波速度；vss为骨架横波速度；ε为裂隙密度；α为裂隙纵横比；ρs为骨架密度；ρfl为孔隙流体密度；vfl为孔隙流体声速；ρf为井孔流体密度；vf为井孔流体声速；R为井孔半径。

图3（见下页）为利用Eshelby－Cheng模型分析的地层纵横波速度，随裂隙纵横比及裂缝密度变化曲线。在模拟过程中，其它参数均采用下页表1中数据，只改变要研究参数的值。由图3可知，纵波和SH 波速度均随裂隙纵横比和裂隙密度的增大而减小，且均变化不明显；而SV 波速度随裂隙纵横比和裂隙密度的增大而减小，且随裂隙密度变化明显。

表1 介质参数Tab.1 Parameters of formation

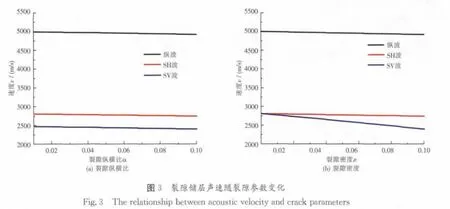
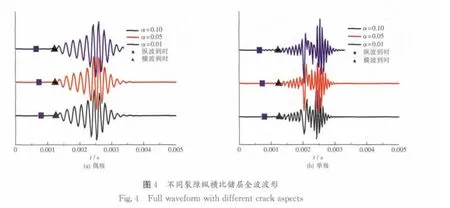
图4（见下页）和图5（见后面）为水平裂隙发育储层不同裂隙纵横比和裂隙密度下的偶极和单极全波波形。其中，正方块和三角形为岩石物理模型计算出的纵波、横波的波至。由图4与图5可知，纵波到时随裂隙纵横比和裂隙密度增大而增大，且变化均不大；但是横波到时和偶极弯曲波波动初至随裂隙密度增大明显，这与图3的岩石物理分析结果一致。

图6为水平裂隙发育储层下弯曲波速度对各参数的灵敏度［10］。由图6可知，在完全弹性地层下，即没有井孔流体和裂隙流体之间的流体交换，弯曲波速度对裂隙孔隙内流体声速的灵敏度最大，且随着频率的增大而减小，弯曲波速度对裂隙密度的灵敏度明显大于对裂隙纵横比的灵敏度。因而，从某种意义上讲，可以利用弯曲波信息提取储层的裂隙密度，但应同时考虑其它对弯曲波影响较大的因素。

图7（见下页）为水平裂隙发育储层下斯通利波速度对各参数的灵敏度。由图7可知，斯通利波速度对井孔内流体声速的灵敏度最大。斯通利波主要反映的是地层流体的流动，而本模型把地层等效成弹性地层，因而斯通利波速度和衰减对裂隙的纵横比和密度的灵敏度较小。

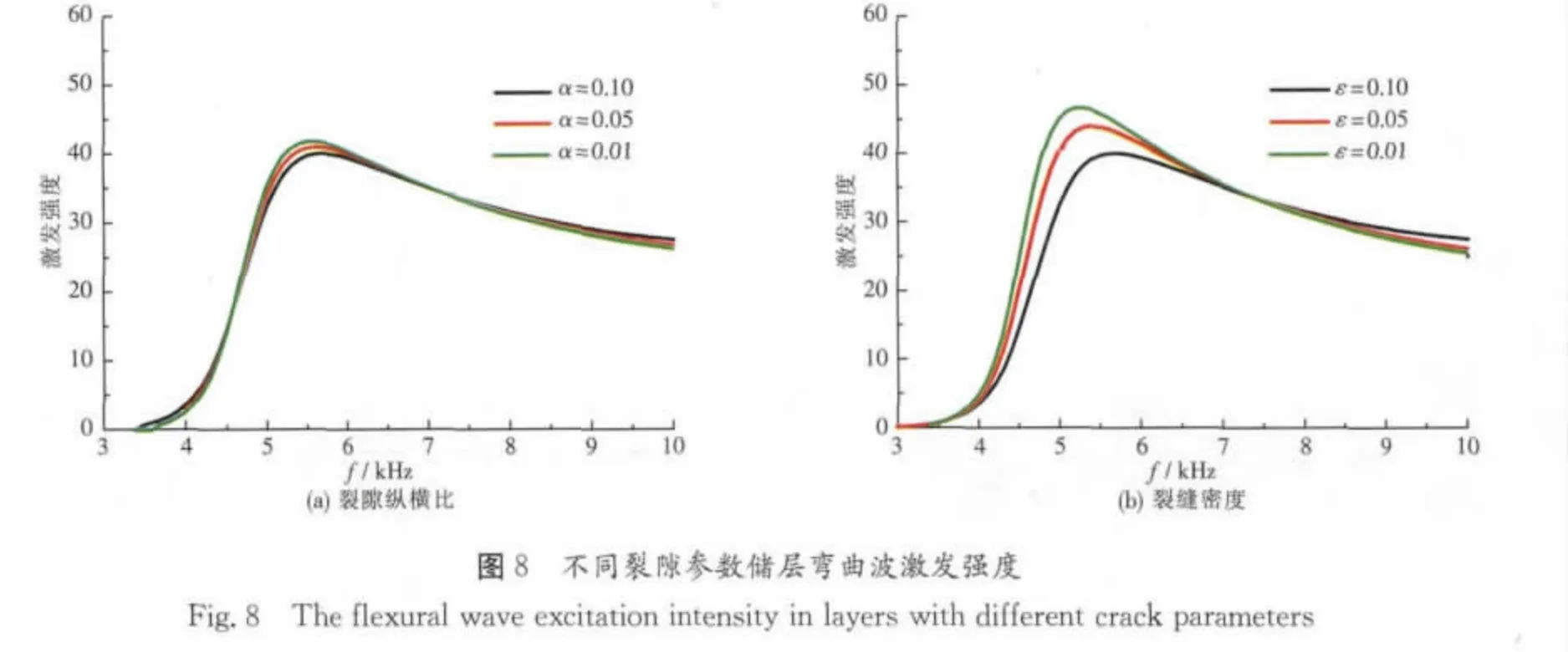
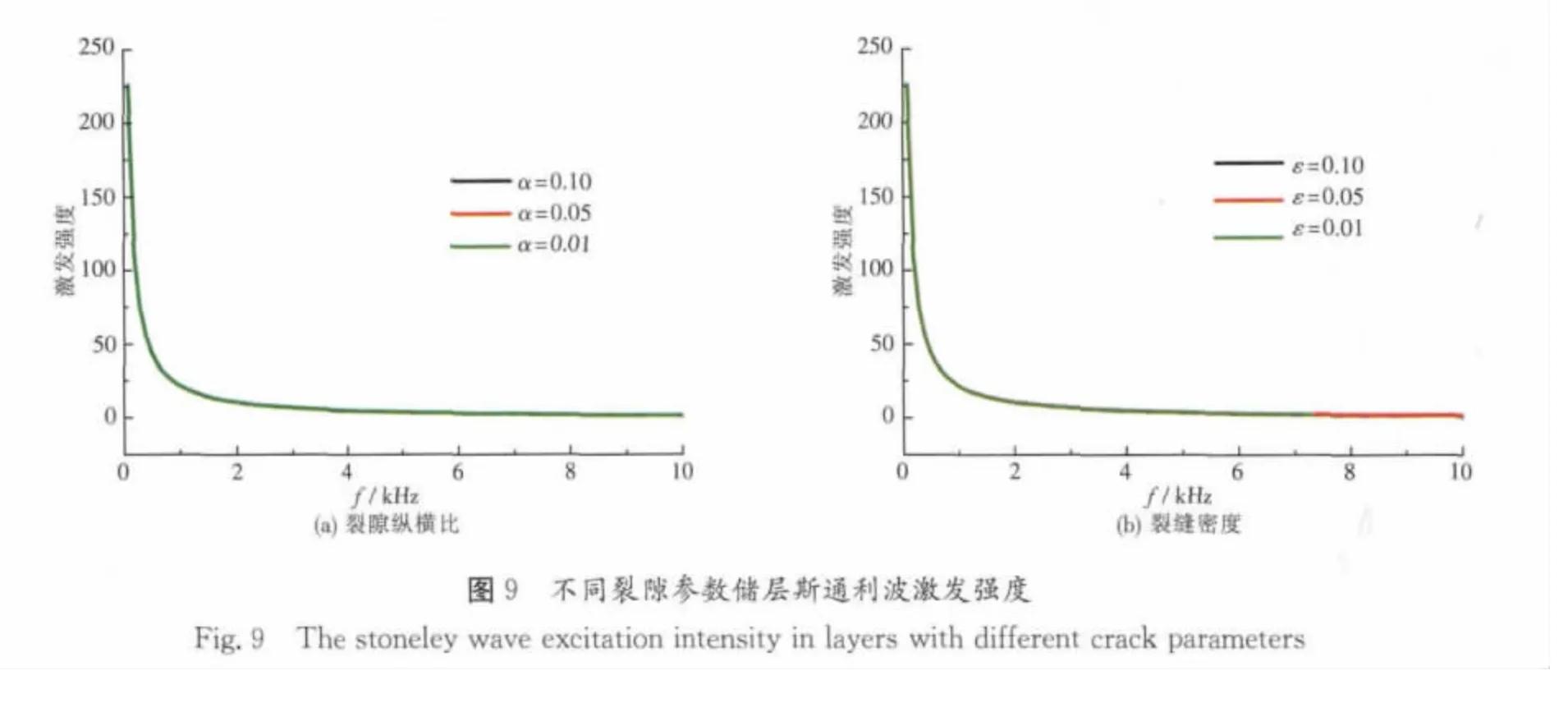
为了研究水平裂隙发育储层斯通利波和弯曲波幅度，作者对不同裂隙下的弯曲波和斯通利波激发强度进行了模拟。其中，图8（见下页）为不同裂隙参数储层弯曲波激发强度；图9（见下页）为不同裂隙参数储层斯通利波激发强度。

由图8及图9可知，斯通利波的激发强度随裂隙纵横比以及裂隙密度变化不大，而弯曲波的激发强度随裂隙纵横比以及裂隙密度的变化较大。在偶极声波测井对应的弯曲波主频附近，随着裂隙纵横比的增大，弯曲波激发强度减小；随着裂隙密度的增大，弯曲波激发强度也减小，且弯曲波激发强度随裂隙密度的变化明显大于随裂隙纵横比的变化。因而在裂隙参数反演中，可以认为裂隙密度是裂隙对弯曲波激发强度中的主要因素。

3 实例分析

图10（见下页）为X1井阵列声波测井成果图。由图10可知，在整个井段中，GR 变化较平缓，因而可以认为整个井段岩石骨架性质变化不大。在3 398m深度附近，纵波、横波时差均有一定程度的增大，且横波变化更为剧烈；斯通利波幅度减小明显，主频有一定程度的减小（即周期变长）；偶极弯曲波幅度减小，波形变窄，主频也有一定程度的减小。以上表征与有裂隙发育储层的声波特征吻合。

从FMI井周成像资料可以看出，该层段有水平裂缝和低角度裂缝发育，如下页的图11所示。

4 结论

（1）由裂隙发育储层的岩石物理模拟可知，SV波对地层的裂隙密度有一定的灵敏度，而纵波对地层裂隙密度的灵敏度较小。

（2）由裂隙发育储层的声波测井数值模拟可知，在将地层等效成完全弹性地层，井孔流体与裂隙内流体没有流体交换时，弯曲波速度及激发强度对裂隙纵横比及裂隙密度有一定的灵敏度，且裂隙密度对弯曲波速度和激发强度的影响尤为明显，这为利用偶极弯曲波数据反演地层裂隙参数提供了理论依据。

［1］桂志先，贺振华，黄德济.裂隙介质弹性性质研究［J］.矿物岩石，2001，21（3）：208.

［2］CRAMPIN S.Seismic wave propagation through a cracked solid：polarization as a possible dilatancy diagnostic［J］.Geophys.J.R.Astr.Soc.，1978，53（3）：467.

［3］HUDSON J A.Wave speeds and attenuation of elastic waves in material containing cracks［J］，Geophys.J.R.Astr.Soc.，1981，64（1）：113.

［4］CHENG C H.Crack models for a transversely isotropic medium［J］.J Geophys Res，1993，98（B1）：675.

［5］THOMSEN L.Biot－consistent elastic moduli of porous rocks：Low－frequency limit［J］.Geophysics，1985，50（12）：2797.

［6］SCHOENBERG M，SAYERS C.Seismic anisotropy of fractured rocks［J］.Geophysics，1995，60（1）：204.

［7］DVORKIN J，NUR A.Dynamic poroelasticity：A unified model with the squirt and the Biot mechanisms［J］.Geophysics，1993，58（4）：524.

［8］唐晓明.含孔隙、裂隙介质弹性波动的统一理论——Biot理论的推广［J］.中国科学：地球科学，2011，41（6）：784.

［9］葛瑞·马沃可，塔潘·木克基，杰克·德沃金.岩石物理手册－孔隙介质中的地震分析工具［M］.徐海滨，戴建春，译.北京：中国科学技术大学出版社，2008.

［10］唐晓明，郑传汉.定量测井声学［M］.北京：石油工业出版社，2004.