基于稳健统计学和EDA 技术的地球化学异常下限确定

Nguyen Tien Thanh ，刘修国 ，陈春亮 ，任 泽，Dang Thai Son

（1.中国地质大学 国际教育学院，武汉 430074；2.河内矿业与地质大学，越南 河内 130510；3.中国地质大学 信息工程学院，武汉 430074；4.中国地质大学 研究生院，武汉 430074；5.越南地质与矿产总局，越南 河内 130510）

0 前言

地球化学异常下限的确定是地球化学勘查的一个基本问题。二十世纪五十年代以来，地球化学家基本认为，地球化学场中的分布接近正态分布或者对数正态分布［1、2、4～9］。因此，使用传统统计方法确定地球化学异常下限时，首先要仔细研究地球化学数据，检验其是否服从正态分布或对数正态分布。为什么数据的分布情况对数据处理有这么重要的影响？因为在传统的统计方法中，相关分析、因子分析、判别分析和经典统计检验包括概率的计算，都是数据在服从正态分布假设的前提下进行的［3］。很多与地球化学相关的文献，都表明地球化学数据往往服从对数正态分布［4～7］。但新的研究表明，元素在地质体中的含量分布，并不局限于正态分布或对数正态分布［2、8、9］，所以数据转换［10～13］（如取对数、余弦、平方根等）和明显特异值（特高值和特低值）的剔除，直到数据服从正态或对数正态分布为止［1、2、9、13］，是两个简单的解决方案。先计 算数据的平均值和标准偏差，然后对全部数据进行异常筛选和评价，一般是以平均值与二倍标准偏差之和作为地球化学异常下限。关键问题是数据转换并不能使数据更接近正态分布［14］，忽略这一点，可能会导致错误的结果。至于明显异常点的剔除，数据处理的最终目的是确定异常点，剔除异常数据之前该如何确定哪些点是异常数据，哪些点不是？这种做法有三种弊病［15、16］：

（1）在很多情况下，尤其在多元情况下，一点不容易被检视数据所鉴别。这是因为在多元情况下，许多点只有在考虑不同变量之间的关系时才显出异常。

（2）剔除异常点的做法，不能保证清理后的数据服从正态分布或方法所要求的某种分布。

（3）从技术的角度来看，对现代社会中自动化观测所积累的大量多元数据，用人工检视来剔除异常点不仅太耗工时，而且不能保证应有的精度和一致性。

此外，传统的统计方法对所研究的总体的分布形式或其它特性有一些假设。当实际总体不满足这些假设，或观测数据中包含不能代表总体性的异常点时，运用传统的统计方法就遇到了问题。应用传统方法有可能导致错误的结果，而且这类错误还往往不容易被觉察。鉴于传统方法的缺陷性，许多其它方法被采用来确定地球化学异常，如杨大欢［9］提出的含量排列法，成功地对广东始兴地区化探数据进行了处理；姚涛［10］以甘肃省白银市白银矿区及外围水系沉积物Cu、Pb、Zn、Ag等四个元素为例，将通过归一化法与其它方法进行比较发现了更多的异常，并且与矿化集中区吻合较好；史长义［17］提出了子区中位数衬值滤波法，该法采用子区模拟背景场的空间变异，以EDA 技术计算异常临界值，以衬值为基准度量场值的起伏变化，较好地解决了弱小异常的识别问题；李随民［18］利用趋势面分析方法把元素的空间分布分解为整体趋势和局部异常两部份，将局部异常从整体中分离了出来；黄静宁［19］对滇东三个不同勘查尺度的水系沉积物地球化学数据，采用地质统计学方法圈定和评价地球化学异常；尤其是Qiuming Cheng［20］提出了含量～面积模式，首次将分形引入地球化学异常的判别，并且在加拿大取得了成功，在中国也引起了很大的轰动。目前该方法国际上应用比较多［21］，也是全国矿产资源潜力评价的推荐方法。

本研究作者介绍了稳健统计方法，该方法具有“稳健”的特点，不太受异常点的影响，并且在EDA技术的支持下来确定地球化学异常下限。以一个具体的地区为例，该方法圈定的地球化学异常符合客观实际，异常范围大，与已知矿床（点）吻合很好。

1 地球化学异常下限的确定

1.1 基于传统统计方法的异常下限确定

传统的统计方法都是以数据要服从正态分布的假设前提下展开的，因此，在化探数据处理之前，首先要认真地研究数据分布。数据是否来自正态总体的检验是至关重要的，正态分布检验是一个不可缺少的步骤。现有很多正态分布检验方法，可以分成图示法和计算法等三类。

（1）图 示 法 是EDA 技 术［22、23］提 供 的 图 形 工具，能够一目了然地看出来数据的分布情况。①简单的直方图是：通过判断是否以钟型分布，箱线图侧观察矩形位置和中位数，若矩形位于中间位置且中位数位于矩形的中间位置，则分布较为对称，否则是偏态分布；②茎叶图是通过观察图形的分布状态，是否是对称分布，使用正态概率图（p－p图和q－q图）判断样本点是否围绕第一象限的对角线分布，如果是，就视为数据服从正态分布。图示法比较直观，方法简单，从图中可以直接判断，无需计算，但这种方法效率不是很高，它所提供的信息只是正态性检验的重要补充。结合直方图、密度图、箱图、一维分散点图和累积分布函数图，能直观地显示出数据的的分布情况。

（2）计算法包括稳健统计技术和非参数方法。最常 用 的 是Kolmogrov－Smirnov 检 验 法［24、25］，Chi－squareχ2拟合检验法［26］和Shapiro－Wilk检验法［27］。这些方法的原理是两个已知分布的样品和未知分布的样品进行比较，计算之后的p值＞0.05，则接受数据服从正态分布的假设。

（3）第三类是偏度、峰度检验法。常用的有S、K 的极限分布，以及Jarque－Bera检验。偏度和峰度都接近“0”，就可以认为该地球化学元素近似服从正态分布［22］。但此类方法的计算结果易受异常值的影响，检验功效就会降低。在实际工作中，可以把多种检验方法结合起来，效果就会更好。

通常认为常量元素接近正态分布，而微量元素接近于对数正态分布。在实际工作中，没有数据完全服从正态分布或者对数正态分布，所以要对原始数据做预处理。通过平均值的计算（mean），再加二倍的标准偏差（sdev），可以得到异常下限（T）。步骤如下：

步骤1：

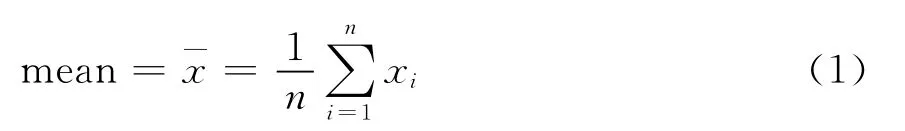
步骤2：

步骤3：

其中 mean为元素含量的平均值；xi为各样品中某元素含量；n为参加计算的样品数；T为异常下限；sdev为标准偏差。

当地球化学数据服从对数正态分布时，先要将原始数据转化为对数；再以含量对数值计算背景上限（背景上限值）或异常下限；最后根据计算值查其真数即得原始数据的异常下限［11］。

1.2 基于EDA 技术和稳健统计方法的异常下限确定

传统统计学方法要求数据以服从正态分布为假设前提，但是通常原始数据不完全服从正态分布或对数正态分布（只接近于正态分布或对数正态分布），因此，导致异常下限确定的合理性值得商榷。是否存在一种不用建立在统计假设条件下的方法（或工具）来处理化探数据？由于传统方法的缺陷性，作者在本文提出了通过稳健统计方法结合EDA 技术的支持，来确定异常下限。该方法的特点是：

（1）少量特异值引起对理想分布型式的偏离，对其结果影响很小。

（2）较多特异值的存在不至于引起灾难性的后果。

稳健统计方法对数据根据某种原则自动加权，从而异常点的影响被不同程度地削弱，直至为零［15、16］。

稳健统计学定义了稳健估计的中位数绝对中位差（mad）和四分位数间距（iqr）［28］。地球化学异常下限可以由［median＋2＊mad］或者［median＋1.5＊iqr］公式来确定［29］，其中，mad由即相对于中位数的偏离绝对值的中位数，如公式（4）所示：

mad＝1.483中位数［｜xi－中位数（xi）］（4）式中 1.483为尺度因子（乘以它使mad与标准差相合）［14，28］。

四分位数间距是指第一分位和第三分位、四分位数两者的差距。mad和iqr类似于传统统计学中的标准离差，所以［median＋2mad］和［median＋1.5＊iqr］类似于［mean＋2sdev］。从上述公式可以看出，与标准离差相比，mad和iqr受异常点的影响较小。

EDA 技术是一种处理数据的非常规统计学方法，它利用稳健统计学和非参数统计学，并引人各种简单而有效的图示技术，从中可迅速看出数据的结构和特点。EDA 不需要任何假设条件，而是根据数据本身所固有的模型来识别异点，由此来确定背景总体和异常总体。利用这些特征，我们可以直接解释原始数据。实践已证明，在单元素地球化学数据的描述和分析中，EDA 技术非常有效［30］。在稳健统计学的基础之上，EDA 定义了箱图，通过它来确定异常下限和了解数据的分布情况。在箱图中，定义了五个参数（最小值、下铰链、中位数、上铰链和最大值），这些参数能够描述数据的重要特点、结构、分布。为了确定这五个参数，首先要对数据进行排序（从大到小或从小到大）；然后取中位数（Q2）。通过中位数排序之后，分成从最小值至中位数与中位数至最大值两部份，分别对这两部份取中位数得到下节点（Q1）和上节点（Q3）。四分位数已确定，通过公式（5）～公式（11）来确定四分位数间距，上（下）铰链，栅栏外下限（上限），异常下限（上限）（如图1所示）：

位于uif和lif之外的所有数据点即为异常点，其中位于uof和uif之外的数据称为远异常（far outliers）。

通过箱图能迅速发现一批数据的下列特征：位置、散度、偏度、尾长、外围数据点数。尤其是从计算异常下限（上限）的公式可以看出，箱图的一个非常重要的特性，就是能够抵抗异常点的影响。也就是说，25%的数据点可能是“野”的，这些“野”值对中位数和上、下节点不产生明显影响［30］。从公式（8）可以看出，异常下限仅由四分位数间距确定，所以，它不会受“野”值（异常值）的影响，因此异常下限确定受数据分布的影响也不严重。

在两个分布的末段（小于lif和大于uif），有可能存在“未发现的异常”，这意味着数据均匀分布。如果要有异常值，作者建议通过百分比或者累计概率图来确定背景值和异常值的边界。针对百分比，95%或者98%的位置可以作为异常边界。在累计概率图中，如果确实有异常值的话，我们将明显看到它们。

图1 箱图示意图Fig.1 Turkey boxplot

2 试验数据

2.1 研究区简介

按照1∶200 000水系沉积物测量，要求我们在一个具体的地区进行取样工作。平均采样密度是每四平方公里一个组合样，每件样品测试项目包括Ag、As、Au、Be、Cd、Cu、Hg、Li、Mn、Mo、Nb、Pb、Sb、Sn、Th、V、W、Y、Zn、Al2O3、CaO、K2O、Na2O 等。在研究区内，主要成矿元素为Cu、Ag、Au，为了探讨基于稳健统计学和EDA技术确定地球化学异常下限的方法，作者初步选取这三个元素进行分析。

2.2 实验结果分析

首先，我们定性地研究该地区的各元素含量的分布情况。使用R 语言中的StaDA 程序包［23］构建直方图、密度图、箱图，一维分散点图和累积分布函数图，它们定性地帮我们了解数据的分布和结构。从图2（见下页）可以看出，三个元素含量都是正偏分布。

表1总结出了三个地球化学元素（Cu、Ag和Au）的计算结果。该表1显示，平均值与中位数和标准偏差与中位绝对中位差之间有一个非常大的偏差。首先进行正态分布检验，为了使检验结果更加可靠，就要采用SPSS 软件中的Kolmogrov－Smirnov检验法（k－s检验）和Shapiro－ Wilk检验法（s－k检验），偏度和峰度不同的正态分布检验方法。由表1获知，三个变量的P值都等于“0”（原假设被拒绝因为P值小于0.05），峰度系数和偏度系数都很大，这说明所有的样本不服从正态分布。

为了进一步检验这些变量是否服从对数正态分布，我们采用对数转换方法。结果表明k－s、s－k检验的P值仍然等于“0”，峰度还是比较大，特别是Cu和Ag元素（如下页图2所示）很相似。这一点证明了转换后的这些变量不服从对数正态分布，因此，未转换或已转换的变量采用传统的统计方法来确定异常下限不符合其假设条件。从图2（见下页）可以看出，与平均值相比，中位数比平均值更好地估计了数据分布的一个总体的中心位置，受影响的异常点的平均值往往比实际值大得多。标准偏差是根据每个观测值离平均值的偏差，由于平均值不能很好地估计样本总体的中心位置，标准偏差不能给出一个较可靠离总体中心位置的范围，因此它严重地受异常点的影响。而中位绝对中位差却不受任何异常点的影响。

对上面所讨论的问题，我们采用了两个简单的解决方案：

（1）先剔除明显的异常点，然后再计算均值和标准偏差。哪些点是异常点，我们根据直方图来判断：Cu有1.5%，Ag有1.5%，Au有3.7%的异常点被剔除。

（2）对原始数据取对数，然后再计算平均值和标准偏差，以含量对数值计算异常下限，最后根据计算值查其真数。

由表1和图4（见后面）可见，这两种方案的计算结果相差很大，第一种方案比第二种方案发现的特高异常点多得多（见下页图2中的黑色），但第二种方案能发现特低异常点（见下页图3 中的浅灰色），即使都是假异常（如图3中的Cu－a、Cu－b、Ag－a、Ag－b和Au－a、Au－b所示）。该地区南方所发现的异常相当小，这跟实际情况不符。该结果具有不确定性，它依赖于明显异常点的剔除和数据转换之后的分布情况。稳健统计方法中的［median ＋2mad］和［median＋2iqr］，比传统的统计方法发现该地区的三个元素含量的异常区域要多。

由后面的图4可以证明，稳健统计学比传统的统计学能更好地判断离群样品（异常点）。通过q－q图发现异常点逐渐偏离于直线，只有稳健统计学才能很好地判断这些点，［median ＋2mad］还能发现特低异常。结合已发现矿床（点）（该地区的矿床（点）分布如下：北向有五个，东北向有四个，东向有一个，南向有二个）可知，该发现与实际情况很吻合。同时发现西北向，西向，西南向，东向有一些地方异常面积比较大，但并没发现有矿床（点），原因是由地质体引起的异常。

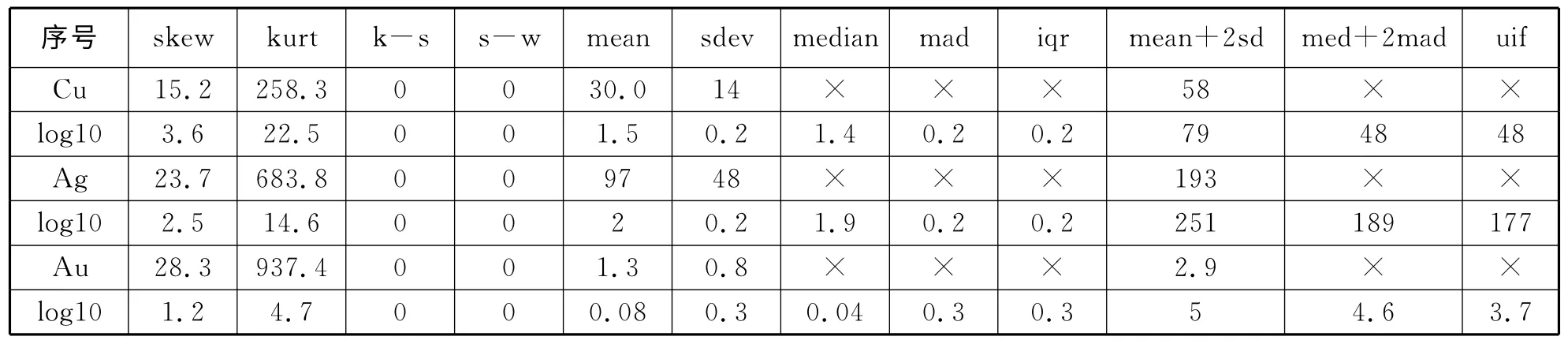
表1 基于传统统计学、稳健统计学和箱图三种异常下限确定方法的异常综合表Tab.1 Comprehensive table of anomalies identified by using traditional statistics，robust statistics and boxplot

3 结论

作者在本文中的研究证明，在传统的统计学的基础上，数据要服从正态分布。原始数据基本不服从对数正态分布和正态分布，数据转换（例如：取对数，余弦，平方根等等）不会导致数据服从正态分布，对进一步的数据处理可能会导致有偏和错误的结果。由于均值和标准偏差不能很好地估计数据的总体中心位置和蔓延（尺度），所以采用均值标准差法求异常下限值得商榷，原因是其数据不满足假设前提。

通过上述的分析可以看出，传统方法比较麻烦（要先取对数，然后再根据计算值查其真数或剔除明显异常），而结果不一定可靠。在大多数情况下，稳健统计方法提供的中位数比平均值能更好地估计数据的中心位置，中位绝对中位差和四分位数间距能很好地估计数据的蔓延。它们都能抵抗特高值和特低值的干扰，不要求数据服从某种分布的假设，因此比传统的统计学能更加有效地处理化探数据。

［1］龚庆杰，张德会，韩东昱.一种确定地球化学异常下限的简便方法［J］.地质地球化学，2001，29（3）：215.

［2］彭省临，杨中宝，李朝艳，等.基于GIS确定地球化学异常下限的新方法［J］.地球科学与环境学报，2004，26（3）：28.

［3］蒋敬业.应用地球化学［M］.武汉：中国地质大学出版社，2006.

［4］AHRENS LH.A fundamental law of geochemistry［J］.Nature，1953（172）：1148.

［5］AHRENS LH.The lognormal distribution of the elements（a fundamental law of geochemistry and it＇s subsidiary）［J］.Geochim Cosmochim Acta，1954（5）：49.

［6］AHRENS LH.The lognormal distribution of elements II［J］.Geochim Cosmochim Acta，1954（6）：121.

［7］AHRENS LH.Lognormal－type distribution.III［J］.Geochim Cosmochim Acta，1957（11）：205.

［8］孙忠军.矿产勘查中化探异常下限的多重分形计算方法［J］.物探化探计算技术，2007，29（1）：54.

［9］杨大欢，郭敏，李瑞，等.一种求地球化学异常下限的新方法－含量排列法［J］.物探化探计算技术，2009，31（2）：154.

［10］姚涛，陈守余，廖阮颖子.地球化学异常下限不同确定方法及合理性探讨［J］.地质找矿论丛，2011，26（1）：96.

［11］罗先熔.勘查地球化学［M］.北京：冶金工业出，2007.

［12］CLIFFORD R，STANLEY.Numerical transformation of geochemical data：1.Maximizing geochemical contrast to facilitate information extraction and improve data presentation［J］.Geochemistry，Exploration，Environment，Analysis，2006，6（1）：69.

［13］史长义.异常下限与异常识别之现状［J］.国外地质勘探技术，1995（3）：19.

［14］王志刚，赵永存，孙维侠，等.基于稳健统计学确定高潜在污染土壤Cu、Pb基线值［J］.土壤学报，2011，48（2）：246.

［15］周蒂，王家华.稳健统计学简介（上）［J］.数理统计与管理，1984：44.

［16］周蒂，王家华.稳健统计学简介（下）［J］.数理统计与管理，1984：41.

［17］史长义，张金华，黄笑梅，等.子区中位数衬值滤波法及弱小异常识别［J］.物探与化探，1999，23（4）：250.

［18］李随民，姚书振，韩玉丑.Surfer软件中利用趋势面方法圈定化探异常［J］.地质与勘探，2007，43（2）：72.

［19］黄静宁.应用地质统计学方法圈定和评价地球化学异常［D］.北京：中国地质大学，2007.

［20］CHENG Q M，AGTERBERG F P，BALLANTYNE S B.The separation of geochemical anomalies from back－ground by fractal methods［J］.Journal of Geochemical Exploration，1994（51）：109.

［21］成秋明，张生元，左仁广，等.多重分形滤波方法和地球化学信息提取技术研究与进展［J］.地学前缘（中国地质大学（北京）；北京大学），2009，16（2）：185.

［22］TURKEY J W.Exploratory data analysis［M］.Reading：Addison－Wesley，1977.

［23］CLEMENS R，PETER F，ROBERT G.Statistical data analysis explained－applied environmental statistics with R［M］.Great Britain：Wiley，2008.

［24］SMIRNOV NV.Table for estimating the goodness of fit ofempirical distributions［J］.Annal Math Stat，1948（19）：279.

［25］AFIFI AA，AZEN SP.Statistical analysis：a computer oriented approach［M］.New York：Academic Press，1979.

［26］CONOVER WJ.Practical nonparametric statistics，2ndedition［M］.New York：J Wiley，1980.

［27］SHAPIRO SS，WILLK MB.An analysis of variance test for normality［J］.Biometrika，1965（52）：591.

［28］胡以铿.地球化学中的多元分析［M］.武汉：中国地质大学出版社，1991.

［29］EMMANUEL J M.CARRANZA.Geochemical anomaly and mineral prospectivity mapping in GIS［M］.The Netherlands，2008.

［30］史长义.勘查数据分析＿EDA＿技术的应用［J］.地质与勘探，1993：52.