稀疏矩阵快速回代的Cholesky分解法

2013-08-07王绪本

物探化探计算技术 2013年3期

宋滔，王绪本

（成都理工大学地球物理学院，成都 610059）

0 前言

在使用有限单元法进行地球物理的数值模拟时，最终需要求解一个大型稀疏线型方程组Ax＝B，而这个线性方程组往往是对称正定的。在解点源问题时，如果采用齐次边界条件，那么矩阵A只和地下电性参数有关，不包含源信息，这个时候只有列向量B包含有源信息。如果使用高斯消元法求解，那么对于每一个电源点都要进行消元和迭代，这大大增加了计算量。阮百尧［1］使用Cholesky分解法，首先将矩阵A分解为两个对称矩阵，对于不同的列向量B只需要进行一次顺代和一次回代便可以求解方程组。但是通过对计算过程的分析发现，其算法的回代过程几乎占用了整个求解过程时间的一半，没有充分利用分解后矩阵的对称性和稀疏性。在此基础上，作者对该算法进行了一定的改进。

1 大型对称稀疏矩阵的变带宽存储

对于变带宽的对称稀疏矩阵，采用二个一维数组来存储［1］，用一个一维数组G存储矩阵的下三角元素，并且以当前行的第一个非零元素开始，以另外一个数组ID存储矩阵中对角元素在矩阵中的位置，那么通过对对脚元素的索引，就可以实现对整个矩阵元素的访问。以下面的5×5对称正定稀疏矩阵为例：

这样G＝（1，2，5，1，1，2，5，1，5），ID＝（1，3，4，7，9），以下的计算均以这个矩阵为例。

2 Cholesky分解法

矩阵A是正定对称的，那么可以使用Cholesky分解法进行计算，即可以得到

从式（3）与式（4）中可以看出，下三角矩阵L中的元素对应矩阵A中下三角的元素，所以分解的结果矩阵L可以使用存储A的二个一维数组来存储索引。由于LT是L的转置，所以LT中的元素也可以使用这二个一维数组来访问。

由于A是稀疏的，含有大量的零元素，所以L和LT中也含有大量零元素，在顺代和回代的过程中应该充分利用这一特性。

上式（2）中矩阵A分解得到：

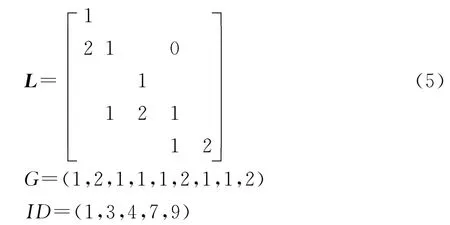
对于线型方程组Ax＝B，即LLTx＝B，进行顺代和回代便可求解。

3 顺代和回代

顺代的求解过程很简单，对于Ly＝B，L是下三角矩阵，只需要依次求解y1、y2、…、yn即可。下一步是求解LTx＝y，由于LT是L的转置，同时共用一个存储空间：

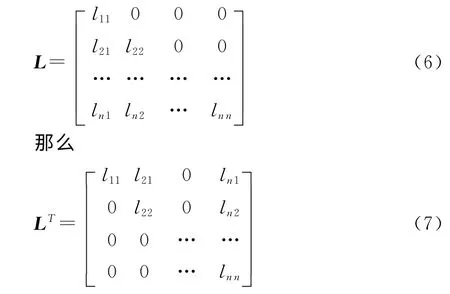
LT是上三角矩阵，通过回代便可完成方程求解。方法（1）：按行依次求解xn、xn－1、…、x1，矩阵元素均可通过矩阵L的索引方式得到；方法（2）：回带的同时，消去方程组中包含当前求解的xi。这两个方法在L非稀疏时，计算时间是一样的，但是当L是稀疏矩阵时，方法（2）的计算效率是非常高的，如下矩阵所示。

使用方法（2）回带时，首先解出x5，然后消去方程组中的x5，即将第5列中的元素消去，因为LT中的列是L中的行，在数组G中是按行存储的，所以这一步骤是很容易实现的。同时，G是压缩存储的，所以在此例中，消去最后一列，仅需要计算一步（消去LT中的l45）。在大型稀疏矩阵中，这种消去列的实现方法，对计算速度的提升是非常可观的。

4 Cholesky分解法的求解程序

！N 整变量，输入参数，方程组的阶数。

！N P 整变量，输入参数，为系数矩阵A压缩存储的元素个数。

！A 输入、输出参数，N P个元素的一维实数组，输入时存放系数矩阵的压缩存储元素；输出时存放。

！Cho lesky 分解得到的下三角阵中变带宽内的元素。

！B 输入、输出参数，N 个元素的一维实数组。输入时存放方程组右端的n维常向量；输出时，存放解。

！向量。

！ID 输入参数，N 个元素的一维整数组。存放系数矩阵A的各个对角线元素在压缩的一维数组中的。

！位置坐标。

5 算例分析

作者将本算法分别用于点源二维电场和二维大地电磁的计算，与传统的cholesky分解算法还有不带平方根的cholesky算法进行对比。在以下计算分析中，所使用的计算机为CPU：T6600，2.2GHz，内存2G。

5.1 点源二维电场的计算

作者采用矩形网格剖分，电导率分块均匀变化，双线性插值有限元进行模拟。x方向（水平沿测线方向）包括100个测区网格，两边分别有12个稀疏网格；y方向（垂直方向）一共设置20个网格，点源点移动100次，即分解后，进行100次回代和顺带。地下空间设置为均匀半空间，分别使用本方法和cholesky分解法求解，如下页表1所示。

从计算结果中可以看出，快速回代的cholesky方法对于点电源场求解速度的提升是非常大的，与传统的顺带回代方法相对比，提升了五倍左右，而且单元数越多，其提升越明显。

5.2 二维大地电磁正演模拟

地面测线长4km，测点间距100m，频率范围为1 000 Hz～0.01 Hz，对数等间隔采样，一共41个频点。

作者采用矩形网格剖分，电导率分块均匀变化，双二次插值有限元进行模拟。x方向（水平沿测线方向）包括41个测区网格，两边分别有18个稀疏网格；y方向（垂直方向）一共设置56 个网格，TE模式下空气网格设置14个。地下空间设置为均匀半空间，分别使用本方法和不带平方根的cholesky分解法求解，如下页表2、表3所示。

从表2、表3可以看出，使用快速回代的cholesky算法的速度，要比传统的cholesky分解法快一倍。