基于统计过程控制技术的XBT 故障概率控制研究
2013-08-06方芳,张鹏,陈晨
方 芳 ,张 鹏,陈 晨
(1.国家海洋技术中心,天津 300112;2.中国烟草江苏省公司扬州市公司,江苏 扬州 225002)
投弃式温度剖面测量仪(the Expendable Bathythermograph,XBT)是一种通过投弃在快速下降过程中感应海水温度剖面的一次性使用的测量系统。它使用方便可靠,测量探头成本低廉,并能进行大范围实时温度剖面数据的快速获取,因此在海洋调查、海洋科考、海洋环境保护、海洋维权、海洋防灾减灾和国防建设等领域均有大量的应用需求。目前,国家海洋技术中心的技术人员已经攻克了投弃式剖面测量的相关关键技术,其测量指标已达到国外同类产品的水平,但海上试验的成功率与国外产品相比还存在差距。本文基于这种情况,探讨了一种利用统计过程控制技术分析XBT海上试验故障的方法。
统计过程控制(Statistical Process Control,SPC)是应用统计技术对过程中的各个阶段进行监控,从而达到改进与保证质量的目的[1]。这里统计技术是指任何可以用于分析和监控过程的统计方法。该种理论可以广泛应用于设计、生产、服务和管理等一般过程。产品的实现过程总是存在波动的。统计技术可以帮助我们了解波动的特性和规律、分析引起波动的根本原因、寻找控制和减小波动的机会。按照统计学的原理,影响过程波动的原因可分为随机因素(正常因素)和系统因素(异常因素)两类。正常波动是指由随机原因引起的、影响相对较小的、其影响是很难通过对过程控制而消除的、在技术上很难根本消除的或消除其影响要花费很大经济代价的、正常的生产过程中允许存在的波动。异常波动是指由系统原因引起的、在生产过程中并不是大量存在的、一旦存在则影响比较显著、比较容易查明和消除的、在正常的过程中不允许存在的波动。用统计规律判别和控制异常因素造成的质量波动,从而使过程处于受控状态的方法称为统计过程控制方法。
统计过程控制(SPC)技术作为测量数据处理的有效方法[2-3],尽可能浅显易懂地表达整个过程状况,从而对整个过程的异常趋势提出预警,以便管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到和提高控制质量的目的。这种方法应用XBT海试结果的主要意义在于,在海试投放的过程中,故障概率总是存在着波动,而这正是我们发现问题并解决的突破口。分析引起波动的根本原因,辨别波动的起因是随机因素还是异常因素引起的。如果波动是随机因素引起的,其影响是很难通过技术从根本上消除的,这在试验过程中是允许存在的波动。而异常波动在试验过程中并不是大量存在的,而一旦存在则影响比较显著、比较容易查明和消除的,这为找到XBT故障的原因提供依据。
1 XBT系统现场试验结果的统计分析
根据2009—2010年XBT系统的海试报告进行归纳,故障原因的归纳是基于报告中的结论来表述的。如表1~表4所示。
2 XBT系统现场试验结果分析
2009—2010年间的4次海试,共进行了19组试验,合计投放126枚测量探头,其中50枚出现故障,故障概率为0.397,详见表5。
对海试报告得到的试验故障现象进行归纳,见表6。
从表6中可以清晰地看出,由于漆包线的问题导致系统出现故障的概率达到了72%。

表1 2009年第一航次海试结果统计

表2 2009年XBT 第三方独立检测结果统计

表3 2009年第二航次海试结果统计
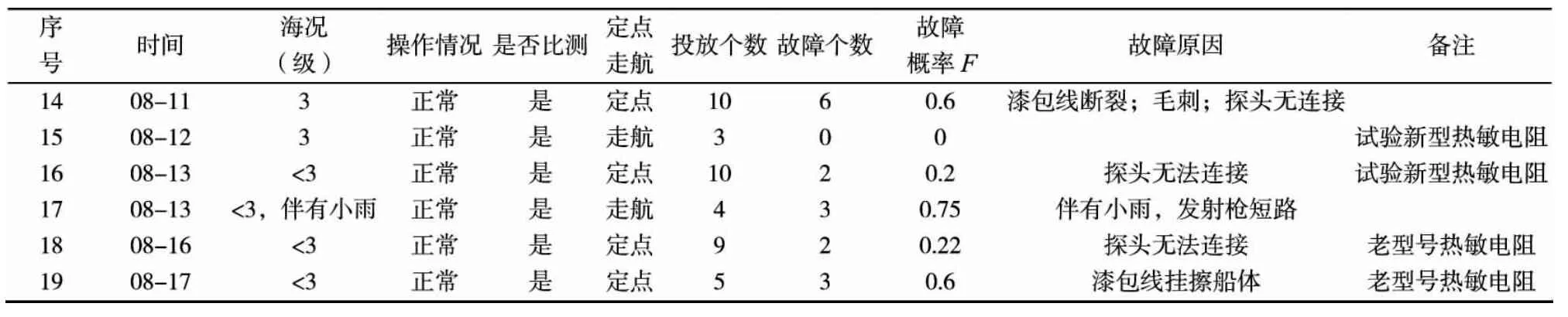
表4 2010年海试结果统计

表5 故障概率统计表
3 过程统计控制(SPC)技术分析现场试验数据的探讨
过程统计控制(SPC)技术的基本要求是抽取的样本来自于同一总体。而在XBT系统现场试验结果的归纳中,存在着由于各航次及各试验阶段所使用的探头,存在着不同程度的零部件的改进、工艺改进、海况和操作不同的情况,因此使用简单的统计方法计算故障概率存在试验条件不统一的问题。因此,首先使用了工程加权法[3]处理现场试验结果,以排除试验条件的影响。该方法的核心思想是对不同条件下的海试结果增加加权因子,将历次海试结果修正到相同的评价条件下,以尽量符合相同的试验条件,达到满足SPC技术分析现场试验数据的要求。考虑到在历次海试中,海况良好,定点投放的情况较多,因此,设定探讨基于如下的评价条件:(1)投放环境按海况三级,天气良好;(2)投放水平严格按照XBT操作流程进行;(3)是否在同一站位相近的时间进行了XBT/CTD的比测试验;(4)投放方式为定点投放;(5)投放个数最少为10枚;(6)技术水平设定为采用改进的零部件。
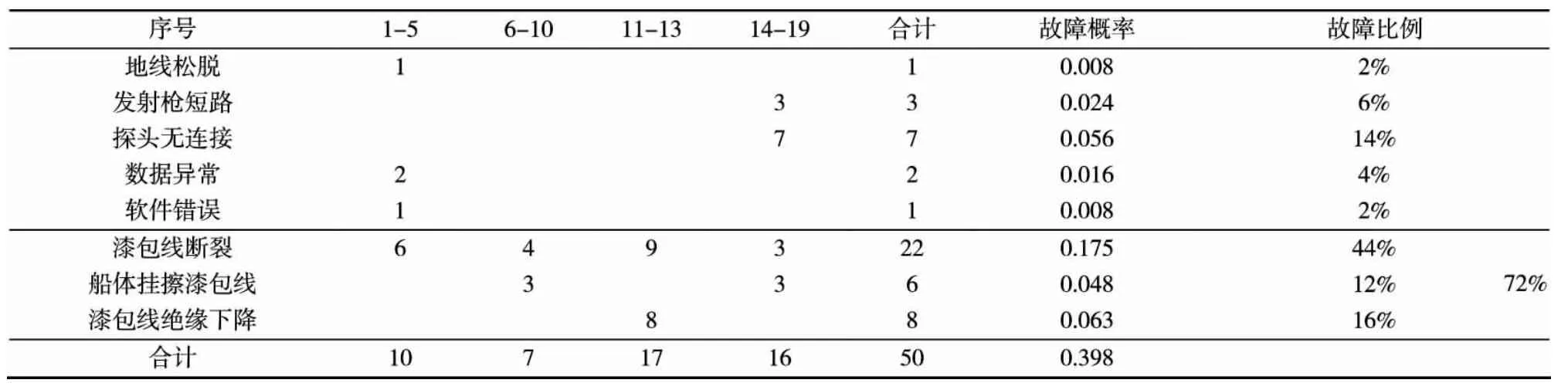
表6 故障现象统计表
3.1 确定各加权因子Ki
加权因子由以下几个方面组成:
(1)环境因子K1:海况不同、天气状况不同投放成功率不同,海况和天气越恶劣,系统故障概率越高,K1取值越小。
(2)操作因子K2:操作是否按照操作规范进行,规范与否造成投放故障概率也不同。操作随意性越大,系统故障概率越高,K2取值越小。
(3)比测因子K3:进行比测的数据较为准确,而未进行比测的数据仅凭主观判断,往往出现判断失误的情况,因此K3取值较大。
(4)投放方式因子K4:走航方式造成系统故障概率越高,K4取值越小。
(5)投放个数因子K5:投放个数小于10个,得出的故障概率没有说服性也失去普遍性,因此K5取值越小。
(6)技术水平因子K6:未改进零部件的系统投放成功率越低,因此K6取值越小。
因子的量值可以采用专家评分法,一般取值0.1~10。标准情况下总加权因子Wi定义为各加权因子之积,如公式(1)所示:

则统一条件下的故障概率F’为:

3.2 重新修正的结果
按照以上的方法,依据公式(1)、公式(2),按照海试的时间顺序,对海试的实际故障概率数据进行重新计算并排序,如表7所示。
在SPC分析过程中使用休哈特先生发明的控制图[4],它利用概率统计原理,做出带有控制界限的曲线图,该曲线由按照时间顺序抽取的数据所得的特性值组成,能够反映过程的趋势。每个抽取的数据在过程控制中称为子组。控制图是由纵轴和横轴构成的简单坐标图。横轴表示子组号,纵轴表示过程特征值。按照各样本点形成的自然顺序(时间先后),将其逐一绘制在坐标图中,并顺序连接为相互衔接的折线,由此形成一张控制图。控制图中还包括3条重要的线,分别是中心线(Central Line,CL),以及中心线两侧的上控制界限(Upper Control Limit,UCL)和下控制界限(Lower Control Limit,LCL)。中心线代表所点绘特性值的基准值,一般为所考察数据的平均值。而上下控制界限分别位于中心线两侧的3σ 距离处。其中,σ 为所点绘统计量的总体组内标准差,也可用子组标准差进行估计。3σ 控制界限表明若过程处于统计控制状态,则大约有99.7%的子组值将落在控制界限之内。

表7 海试结果重新统计分析表
控制图的种类是多种多样的,在本文中使用的控制图是计数控制图中的一种——p 控制图。p 控制图是一种基于二项统计分布的计数型控制图,它绘制的是每个样本的不合格率。其中二项分布是以Bemoulli试验为依据[5],每个试验都将产生两个可能的输出,即“通过”和“不通过”。而样本的试验必须满足以下的条件:(1)每个试验应是独立的,一次试验的输出不能影响另一次试验的输出;(2)对于每个试验来说,只能有两个可能输出中的一个输出;(3)样品的试验数必须是正整数;(4)对所有试验来说,成功或者故障的概率必须是相同的。
满足以上的条件,得到控制限公式如表8所示。
每个子组样本可以有相同的样本量或者不相同的样本量。若子组大小随子组不同而发生变化,则对于每个子组都要计算出各自单独的控制界限。
按照上述方法,进一步分析海试结果。首先现场试验的结果服从成功或者故障这两种不连续的输出,且投放探头的故障概率是相同的,服从二项统计分布,符合p 控制图的使用条件,其中绘制的是每个子组中的故障概率。
首先将按照时间顺序排列的序号作为子组号,将上文重新处理的统计表进行重新归纳,如表9所示。
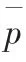
由于各组样本量大小不同,因此对每个子组按照表中p控制图的上控制限(UCL)和下控制限(LCL)公式计算,计算得出海试结果UCL及LCL统计表如表10所示(其中UCL得到大于1的值,一律按照1计入表中;LCL得到小于0的值,一律按照0计入),画出p 控制图如图5所示。

表8 p 控制图的控制限公式

表9 海试结果故障率分析
根据上面的分析,可以发现,由于各组的样本量不同,因此分别绘制上下限非常费时,这时考虑修正过且处理后的故障概率,由于在对实际的故障概率处理时,考虑到了投放个数因子,处理后的故障概率假设为每个子组投放个数为10个,因此对处理后的概率重新绘制p 控制图,求处理后故障概率平均值:
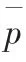
取各子组的平均样本大小n=10,重新标绘p 控制图的上下限,如下:

计算得到的LCL值为负值,以0计。
得到修正后的p 控制图,如图6所示。
以国产XBT系统目前的制造水平及设计水平,故障概率的上限为82%,虽然现场数据分析的结果以及预计的结果均处于上限范围之内,但也可以判断,除了随机因素(比如天气恶劣因素,人员使用不当等)是造成系统成功率不高的原因之外,切实提高系统本身的固有可靠性才是提高系统成功率的根本,尤其是在海试现场中表现较为明显的由于漆包线、探头壳体、发射枪的制造工艺问题造成的故障,是值得我们进一步分析改进的。

表10 海试结果UCL 及LCL 统计表
另外,要注意的是,由于每阶段投放探头数量约在5~8枚左右,试验样本数量较少,各项比测和一致性检验不足以反映XBT系统性能的真实情况成为进行SPC控制的一大障碍。

图5 海试结果p 控制图

图6 修正后的p 控制图
4 结语
将统计过程控制的方法应用于XBT海上试验的故障概率控制中来,一方面对历年的投放故障概率情况进行了监控,另一方面也从中区分出故障概率的随机波动、异常波动,从而分析出XBT投放故障概率波动的范围(即上下限)、平均值以及故障概率波动的原因,找到XBT投放出现故障的因素。分析证明,该方法对于研究XBT的海上试验的故障概率控制具有一定的意义。
[1]张增照.以可靠性为中心的质量设计、分析和控制[M].北京:电子工业出版社,2010:296-297.
[2]钟伦燕.统计过程控制(SPC)技术原理和应用[M].北京:电子工业出版社,2000:12-13.
[3]陈炳生.电子设备可靠性工程系统设备的可靠性理论与实践[M].北京:国防工业出版社,1987:95-97.
[4]国家质量技术监督局.GB/T 4091-2001.常规控制图[S].北京:中国标准出版社,2001.
[5]中国国家标准化管理委员会.GB/T 4087-2009.数据的统计处理和解释二项分布可靠度单侧置信下限[S].北京:中国标准出版社,2009.
