基于间接综合算法的线要素综合及程序实现

王堃，李篷，姜楠

(安徽理工大学测绘学院，安徽淮南 232001)

空间数据线要素的综合算法被很多学者认为是地图综合和GIS空间数据的多比例尺表达与处理中最重要的算法之一［1］，其目的是在保持线的弯曲特征、复杂程度的情况下，尽量减少线要素的存储量。近些年来，有关线要素综合的算法很多，大都是从曲线的几何特征出发，通过删除曲线上的某些坐标点而同时保留特征点来进行简化的［2］。但是在许多应用中常常无法满足精度需求，需要寻求积极的方法来解决。本文主要讨论用间接综合方法处理并通过实例验证其综合效果，探讨利用线要素综合方法和分弧段数据处理方法［3］对大比例尺线要素进行综合的原理和数据处理方法的有关问题。

1 间接综合算法

间接综合算法先直接将原始线要素上的点进行直接变换到目标比例尺空间中。在目标比例尺空间中进行间接判断，再回到源数据比例尺空间中进行取舍。这种取舍的步骤包括:在目标比例尺空间进行重复点的判断，冲突判断，毛刺剔除，冲突移位处理以及特殊情况的判断等，重复此取舍过程，获得原线要素所有的综合后的选择点，组成综合后的线要素。这种算法具有避免抖动、避免自相交、最小变形、保持特征等优点。综合结果同时具有光滑与简化的效果，具有参数设置简便、计算简单、适于快速处理等优点，但是保留的数据量很多，数据压缩量小［4］。

1.1 数据处理的条件方程

(1)长度条件方程

在地图综合实际应用中，要保证综合前后的弧段长度不变。由综合前后弧段的长度相等可以建立弧段的长度条件方程如下:

任意两点间的长度条件方程

将坐标观测值及其改正数代入，并用泰勒公式展开取至一次项，得到条件方程为:

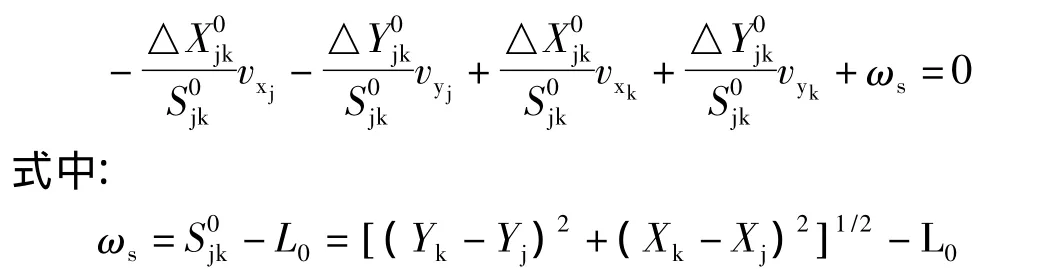
由此可以得到j，k两点的坐标值的改正系数，由此可以递归推下去，从而得到各个子弧段的各坐标长度条件方程改正数系数。

(2)面积条件方程

根据综合前后某一行政区域或地类边界多边形面积不变可建立弧段面积条件方程，如图1所示。

图1 弧段面积条件图

如图1弧段综合前与Y轴围成的面积S前，弧段综合后与Y轴围成的面积S后。该弧段平差后与综合前的面积差G如下式所示:

最后，将各个弧段累加即可以得到整个弧段的面积条件方程。

(3)端点相等条件方程

如图1，根据端点相等可以建立条件方程:

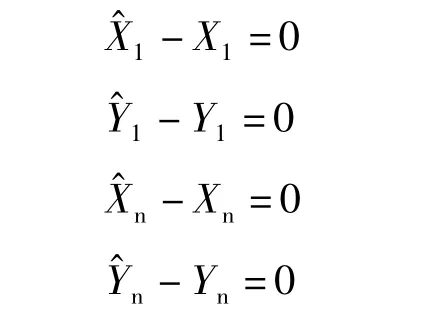
最后的平差需要长度条件方程、面积条件方程以及以上4个首末端点相等条件方程联立对综合后数据进行条件平差。所谓条件平差就是在一个几何模型中有r个多余观测，就产生r个条件方程，以条件方程为函数模型的平差方法。要求在满足r个条件方程式条件下，求函数VTPV=min的V值，在数学中是求函数的条件极值问题。

2 VB程序设计

以过程中的“变换”步骤为例。点击“变换”，程序根据输入的已知数据计算得到转换后的数据，具体代码如下:

2.1 程序实现过程

图2 程序实现流程图

其中多边形的数据输入是指将以Excel或者TXT形式存储的多边形坐标数据导入CAD中展点并绘制成图，且在CAD图形中可随意查取任意一点的坐标值，把多边形按结点划分为等顶点的弧段后，多边形的面积及周长即可累加求出(计算面积和长度是顶点坐标应按逆时针方向计算)。

图3 间接综合算法变换步骤

图4 间接综合算法重复点判断及取舍步骤

3 实例

以图5为例，将图5中的图形利用间接综合算法进行综合，对于综合后的数据进行平差处理。表1为多边形综合前的顶点数、多边形面积、周长、弧段数等数据;表2、表3、表4为多边形按间接综合算法综合后的数据与综合前相应数据的差值数据(综合前比例尺为1∶2000，综合后比例尺为 1∶100000，目标比例尺最小可视目标直径SVO=0.4 mm);表5为按弧段分区平差后的多边形弧数据与综合前相应数据的差值数据;表6为平差值中误差数据。

图5 综合前行政边界图

综合前相关信息 表1

3.1 综合后数据处理结果

截取局域差异较大的弧段进行放大显示，如图6所示。

图6 综合后与综合前图形差异图

在图6中实线2代表综合前弧段，实线1代表综合后的弧段。数据进行处理如表3、表4所示。

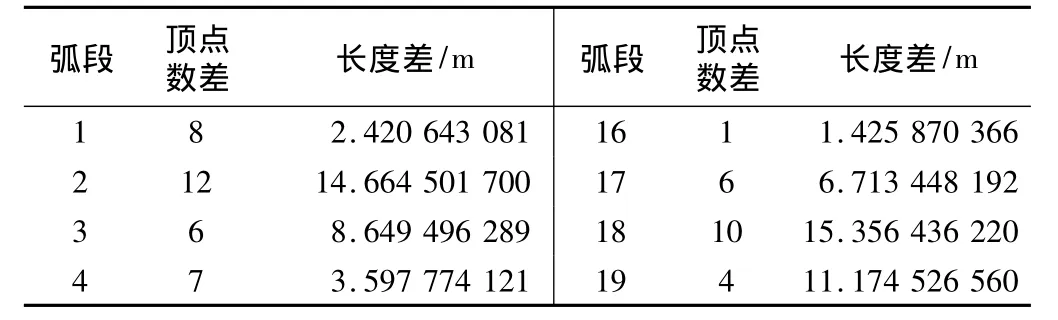
综合前后弧段数据比较表 表2

5 2 3.853465997 20 0 06 1 2.027082894 21 2 －0.0313376907 3 3.506326174 22 1 1.7825907328 5 3.538195816 23 4 2.4021677439 5 1.478334440 24 5 6.77579120910 4 7.044681141 25 8 8.95616875211 4 1.975197093 26 3 5.76244027512 1 1.092677412 27 3 3.57002449013 0 0 28 0 014 0 0 29 1 0.13531478815 1 4.015075251 30 0 0

综合前后数据差表 表3

综合前后各弧段与坐标轴围成的面积差值表 表4

3.2 平差后图形和数据

利用间接综合算法对图形综合后，对行政边界界线按弧段分区进行平差，每一弧段分别列出长度条件方程、面积条件方程以及4个首末端点相等的条件方程［5］。截取相同区域平差后与综合前的图形比较，如图7所示。

平差后与综合前面积与周长比较表 表5

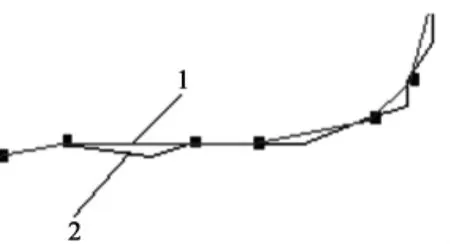
图7 平差后与综合前图形比较图

图7中，实线2为综合前弧段形状，实线1为平差后弧段形状。由于平差的过程消除了综合后的闭合差，所以如表6中平差后与综合前的面积和周长的差值均较平差前小。同一弧段平差前图6与平差后的图7相比较，弧线也更贴合于折线(由于放大倍数的原因，效果不是很明显)。

平差值中误差计算表 表6

4 结论

(1)用间接综合算法对数据进行数据处理，得出平差后与综合前的面积差是 －2.4883 m2，长度差是－2.0832 m，由此可见在综合过程中的变化是比较小的，基本上满足了我们所规定的条件;

(2)平差后所得到的Mx、My、Mp是衡量这个算法与其他算法精度高低的重要标准，其值越小则代表其精度越高，反之，则低。但是综合算法的综合结果与原始图形存在差异，主要是综合的不确定性［6］所造成的;

(3)利用VB程序设计完成了间接综合算法的编程，并对综合前、综合后、平差后的数据进行了分析和比较。通过数据的分析和比较，认为这种算法是一种比较可取的算法。

［1］Wang Z S，Müller J C.Complex Coastline Generalization［J］.Cartography and Geographic Information System，1993，20(2)，96 ～106.

［2］童小华，史文中，刘大杰.GIS中数字化数据误差的分布检验与处理［J］.武汉测绘科技大学学报，2000(01)79～84.

［3］史文中.空间数据处理理论与方法［M］.北京:科学出版社，1998，128 ～130.

［4］雷伟刚，刘大杰，童小华.空间线要素综合算法的不确定性讨论［J］.测绘工程，2005，(1)33～36.

［5］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2003.

［6］雷伟刚.空间数据线要素综合的不确定性与数据处理［D］.上海:同济大学，2004.